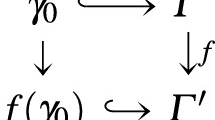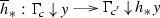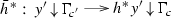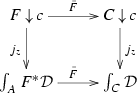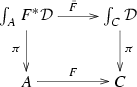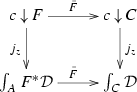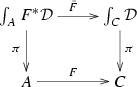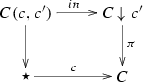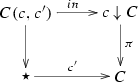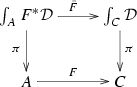Homotopy colimits of 2-functors

Abstract

Like categories, small 2-categories have well-understood classifying spaces. In this paper, we deal with homotopy types represented by 2-diagrams of 2-categories. Our results extend lower categorical analogues that have been classically used in algebraic topology and algebraic K-theory, such as the homotopy invariance theorem (by Bousfield and Kan), the homotopy colimit theorem (Thomason), Theorems A and B (Quillen), or the homotopy cofinality theorem (Hirschhorn).

1 Introduction

If C is any small 2-category, by replacing its hom-categories C(x, y) by their classifying spaces |C(x, y)|, one obtains a topological category whose Segal classifying space  [30] is, by definition, the classifying space $|\!|C |\!|$ of the 2-category C. By this assignment $C\mapsto |\!|C|\!|$, for example, 2-groupoids (or, equivalently, crossed modules in the sense of Brown and Higgins) correspond to homotopy 2-types (i.e., to CW-complexes whose n $\mathrm {th}$ homotopy groups at any base point vanish for $n\ge 3$)  [8, 28], and, up to group completion, monoidal categories (regarded as 2-categories with only one object) correspond to delooping spaces of the classifying spaces of their underlying categories  [31]. A natural interpretation of the classifying space $|\!|C|\!|$, in terms of charted C-bundles, is given in  [3].

The category $\mathbf {2}\mathbf {Cat}$ of (small) 2-categories and 2-functors has a Thomason-style model structure,¹ such that the classifying space functor $C\mapsto |\!|C|\!|$ is an equivalence of homotopy theories between 2-categories and topological spaces. This fact was first announced in  [35, Theorem 4.5.1], but fully proved in  [1, Théorème 6.27].² In [14, Theorem 4.5 (ii)], an extension of the celebrated Thomason’s homotopy colimit theorem  [34, Theorem 1.2] asserts that, for any category C and functor $\mathcal {D}:C\rightarrow \mathbf {2}\mathbf {Cat}$, the 2-category $\int _{C}\mathcal {D}$, obtained by applying the Grothendieck construction on $\mathcal {D}$, is a model for its homotopy colimit (with respect to the Thomason model structure in $\mathbf {2}\mathbf {Cat}$). In other words, the induced functor between the homotopy categories $\int _C -:\mathrm {Ho}(\mathbf {2}\mathbf {Cat}^C)\rightarrow \mathrm {Ho}(\mathbf {2}\mathbf {Cat})$ is left adjoint to the functor assigning to any 2-category the constant functor on C that it defines.

This paper focuses on the study of “homotopy colimits” of 2-functors $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, from an indexing 2-category C into the 2-category ${\underline{\mathbf{2Cat}}}$ of 2-categories, 2-functors, and 2-natural transformations, and our results extend lower categorical analogues classically used in algebraic topology and algebraic K-theory. We shall stress that the main difference with the case of diagrams $\mathcal {D}:C\rightarrow \mathbf {2}\mathbf {Cat}$, where C is a category, is that now there are 2-cells $\phi :p\Rightarrow p'$ in C that produce 2-natural transformations $\mathcal {D}\phi :\mathcal {D}p\Rightarrow \mathcal {D}p'$, and therefore homotopies between the induced maps on classifying spaces by the associated 2-functors $\mathcal {D}p$ and $\mathcal {D}p'$, which must be taken into account. However, a warning is needed since, for now, there is no known model structure in the 2-category ${\underline{\mathbf{2Cat}}}$ having the Thomason model structure in the underlying category $\mathbf {2}\mathbf {Cat}$. So we are not actually correct to speak of ($\mathbf {Cat}$-enriched) homotopy colimits of such 2-functors $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$. However, as we shall prove in the paper, the Grothendieck construction 2-functor

enjoys so many desirable homotopy properties, with respect to the Thomason model structure on $\mathbf {2}\mathbf {Cat}$, that it deserves to be thought of as the correct “homotopy colimit” construction on 2-diagrams of 2-categories.

Interesting 2-diagrams of 2-categories naturally arise from basic problems in homotopy theory of 2-categories. For example, the analysis of the homotopy fibres of the map $|\!|F|\!|:|\!|A|\!|\rightarrow |\!|C|\!|$ induced on classifying spaces by a 2-functor $F:A\rightarrow C$ leads to the study of the 2-functor $F\!\downarrow \!-: C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, which associates to each object $c\in C$ the comma 2-category $F\!\downarrow \!c$, whose objects are 1-cells in C of the form $p:Fa\rightarrow c$. A relevant result here is the extension of Quillen’s Theorem B for 2-functors in  [14, Theorem 3.2], which assures us that, under reasonable necessary conditions, the sequences $F\!\downarrow \!c\hookrightarrow A\rightarrow B$ are homotopy-fibre sequences in $\mathbf {2}\mathbf {Cat}$ (with respect to the Thomason model structure). See also the relative Quillen’s Theorem A for 2-functors in  [18, Théorèm 2.34].

There is another interesting source for 2-diagrams of 2-categories: The study and classification of opfibred 2-categories. The well-known Grothendieck correspondence between covariant pseudo-functors and opfibred categories  [24] has been generalized to bicategories in  [4, 9], where the authors prove, in particular, that the Grothendieck construction on 2-functors $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ gives rise to 2-categories $\int _C\mathcal {D}$ endowed with a split 2-opfibration over C, and this correspondence $\mathcal {D}\mapsto \int _C\mathcal {D}$ is the function on objects of an equivalence between the 3-category of 2-functors $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ and the 3-category of split 2-opfibred 2-categories over C.

The plan of the paper is as follows. After this introductory section, the paper is organized into five sections. Section 2 is preliminary and comprises some notations and a brief review of facts used later. This is itself subdivided into four sections with summaries concerning geometric realizations of bisimplicial sets, classifying spaces of 2-categories, the Grothendieck construction on 2-functors valued in ${\underline{\mathbf{2Cat}}}$, and the homotopy-fibre 2-functors respectively. Section 3 includes a main result of the paper, which we call the Homotopy Colimit Theorem for 2-diagrams of 2-categories. With Thomason’s homotopy colimit theorem as its natural precedent, the result therein states that, for any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the geometric realization of 2-category $\int _C\mathcal {D}$ has the same homotopy type as the simplicial 2-category (i.e., simplicial object in $\mathbf {2}\mathbf {Cat}$)

$$\begin{aligned} \mathcal {B}_C\mathcal {D}:\Delta ^{\!\mathrm {op}}\rightarrow \mathbf {2}\mathbf {Cat}\end{aligned}$$

obtained by applying the bar (Borel or simplicial replacement) construction on $\mathcal {D}$; that is, the simplicial 2-category whose 2-category of p-simplices is

$$\begin{aligned} \mathcal {B}_C\mathcal {D}_p= \coprod _{c_0,\ldots ,c_p} \mathcal {D}_{\!c_0}\!\times C(c_0,c_1)\times C(c_1,c_2)\times \cdots \times C(c_{p-1},c_p). \end{aligned}$$

Hence, both constructions $\mathcal {B}_C-$ and $\int _C-$ can be interchanged for homotopy purposes. The proof of this theorem is quite long and technical, but the result is crucial and many further results are based on it. Section 3 also includes the Homotopy Invariance Theorem, stating that if $\mathcal {D}\rightarrow \mathcal {E}$ is a 2-transformation that is locally a weak equivalence, then the induced $\int _C\mathcal {D}\rightarrow \int _C\mathcal {E}$ is also a weak equivalence. In Sect. 4, we deal with questions such as: When does a 2-transformation $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$, between 2-functors $\mathcal {D},\mathcal {E}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, induce a homotopy left cofinal 2-functor $\int _C\Gamma :\int _C\mathcal {D}\rightarrow \int _C\mathcal {E}$? Or when are the canonical squares ($c\in \mathrm {Ob}C$, $y\in \mathrm {Ob}\mathcal {E}_c$)

homotopy pullbacks? Our main results here are actually extensions of the well-known Quillen’s Theorems A and B for functors between categories to morphisms between 2-diagrams of 2-categories. The final Sect. 5 is dedicated to analyzing the behavior of the Grothendieck construction when a 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ is composed with a 2-functor $F:A\rightarrow C$. There is a canonical 2-functor $\int _AF^*\mathcal {D}\rightarrow \int _C\mathcal {D}$, and we mainly study when this 2-functor is a weak equivalence or, more interestingly, when the canonical pullback square in $\mathbf {2}\mathbf {Cat}$

is a homotopy pullback.

2 Preliminaries

This section aims to make this paper as self-contained as possible; hence, at the same time as fixing notations and terminology, we review some needed constructions and facts concerning geometric realizations of bisimplicial spaces (Sect. 2.1), classifying spaces of (small) 2-categories (Sect. 2.2), the Grothendieck construction on 2-functors valuated in the 2-category of 2-categories (Sect. 2.3), and the homotopy-fibre 2-functors (Sect. 2.4). Although most of the material here is perfectly standard by now, so the expert reader may skip it, some notational conventions may be a bit idiosyncratic for some readers.

2.1 Geometric realizations of bisimplicial sets

For the general background on simplicial sets, refer to [7, 22]. As usually, $\Delta$ denotes the category of finite ordered sets $[p]=\{0,\ldots ,p\}$ with non-decreasing maps between them as morphisms. Recall that it is generated by the injections $d^i:[n-1]\rightarrow [n]$ (cofaces), $0\!\le i\!\le n$, which omit the ith element and the surjections $s^i:[n+1]\rightarrow [n]$ (codegeneracies), $0\!\le i\!\le n$, which repeat the ith element, subject to the well-known cosimplicial identities: $d^j d^i=d^i d^{j-1}$ if $i\!<j$, etc. Thus, in order to define a simplicial object in a category $\mathcal {E}$, say $S:\Delta ^{\!\mathrm {op}}\rightarrow \mathcal {E}$, it suffices to give the objects (of n-simplices) $S_n$, $n\ge 0$, together with morphisms

satisfying the well-known basic simplicial identities: $d_id_j=d_{j-1}d_i$ if $i\!<j$, etc.

In  [30], Segal extended Milnor’s geometric realization process for simplicial sets to simplicial (compactly generated Hausdorff topological) spaces. The realization |S| of a simplicial space $S:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {Top}$, is as follows: for each $n\ge 0$, let $\Delta ^n$ denote the standard n-dimensional affine simplex and for each map $\alpha :[n]\rightarrow [m]$ in $\Delta$ let $\alpha _*:\Delta ^n\rightarrow \Delta ^m$ be the induced affine map (i.e., $\alpha _*(t_0,\ldots ,t_n)=(t_0^\prime ,\ldots ,t_m^\prime )$ with $t_i^\prime =\sum _{\alpha (j)=i}t_j$). Then the space |S| is defined from the topological sum $\coprod _{n\ge 0} S_n\times \Delta ^n$ by identifying $(S\alpha (x),t)\in S_n\times \Delta ^n$ with $(x,\alpha _*t)\in S_m\times \Delta ^m$, for all $x\in S_m$, $t\in \Delta ^n$, and $\alpha :[n]\rightarrow [m]$ in $\Delta$. For instance, by regarding a set as a discrete space, the (Milnor’s) geometric realization of a simplicial set $S:\Delta ^{\!{^\mathrm {op}}}\rightarrow \mathbf {Set}$ is |S|. A weak homotopy equivalence of simplicial sets is a simplicial map whose geometric realization is a homotopy equivalence or, equivalently, induces isomorphisms in homotopy groups.

A bisimplicial set is a functor $S:\Delta ^{\!{\mathrm {op}}}\times \Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {Set}$. This amounts to a family of sets $\{S_{p,q};\, p,q\ge 0\}$ together with horizontal and vertical face and degeneracy operators

with $0\!\le i\!\le p$ and $0\!\le j\!\le q$ respectively, such that, for all p and q, both $S_{p,\bullet }$ and $S_{\bullet ,q}$ are simplicial sets and the horizontal operators commute with the vertical ones. Note that, on the one hand, any bisimplicial set S provides two simplicial objects in the category of simplicial sets: the horizontal one $S^h:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {SSet}$, $[p]\mapsto S_{p,\bullet }$, and the vertical one $S^v:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {SSet}$, $[q]\mapsto S_{\bullet ,q}$. Then, by taking geometric realization, S gives rise to two simplicial spaces $[p]\mapsto |S_{p,\bullet }|$ and $[q]\mapsto |S_{\bullet ,q}|$. On the other hand, the bisimplicial set S also provides another simplicial set $\mathrm {Diag}S:[p]\mapsto S_{p,p}$, whose face and degeneracy operators are given in terms of those of S by the formulas $d_i=d_i^hd_i^v$ and $s_i=s_i^hs_i^v$, respectively. It is known (e.g. [29, Lemma in page 86]) that there are natural homeomorphisms

$$\begin{aligned} |[p]\mapsto |S_{p,\bullet }||\cong |\mathrm {Diag}S|\cong |[q]\mapsto |S_{\bullet ,q}||, \end{aligned}$$

(1)

and we usually take the geometric realization $|\!|S|\!|$ of the bisimplicial set S to be

$$\begin{aligned} |\!|S |\!|=|\mathrm {Diag}S|. \end{aligned}$$

(2)

The following relevant fact is used several times along the paper (see [7, Chapter XII, 4.2 and 4.3] or [22, IV, Proposition 1.7], for example):

Fact 2.1

If $f:S\rightarrow S^\prime$ is a bisimplicial map such that the maps $|f_{p,\bullet }|: |S_{p,\bullet }|\rightarrow |S^\prime _{p,\bullet }|$ are homotopy equivalences for all p, then so is the map $|\mathrm {Diag}f|: |\mathrm {Diag}S| \rightarrow |\mathrm {Diag}S^\prime |$.

We will use also the $\overline{W}$-construction on a bisimplicial set by Artin and Mazur  [2, Sect. III], also called its “codiagonal” or “total complex”. Recall that, by viewing a bisimplicial set $S:\Delta ^{\!{\mathrm {op}}}\times \Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {Set}$ as a horizontal simplicial object in the category of vertical simplicial sets, $S:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {SSet}$, then the set of n-simplices of $\overline{W}S$ is

$$\begin{aligned} \left\{ (t_{n,0}, \dots ,t_{0,n})\in \prod _{p+q=n}S_{p,q}~~\Bigg |~d^h_0t_{p,q}=d^v_{q+1}t_{p-1,q+1} \text { for } \, n\ge p\ge 1 \right\} \end{aligned}$$

and, for $0\le i\le n$, the faces and degeneracies of an n-simplex are given by

$$\begin{aligned} d_i(t_{n,0}, \dots ,t_{0,n})= & {} (d_i^ht_{n,0},\dots ,d_1^ht_{n-i+1,i-1}, d_i^vt_{n-i-1,i+1},\dots ,d_i^vt_{0,n}), \\ s_i(t_{n,0}, \dots ,t_{0,n})= & {} (s_i^ht_{n,0},\dots ,s_0^ht_{n-i,i}, s_i^vt_{n-i,i},\dots ,s_i^vt_{0,n}). \end{aligned}$$

There is a natural Alexander-Whitney-type diagonal approximation $\mathrm {Diag}\,S\rightarrow \overline{W}S$,

$$\begin{aligned} S_{n,n}\ni t\mapsto \big ((d_1^v)^nt,(d_2^v)^{n-1}d_0^ht,\dots , (d_{p+1}^v)^{n-p}(d_0^h)^pt,\dots , (d_0^h)^nt\big ), \end{aligned}$$

inducing a homotopy equivalence on geometric realizations (see [16, 32, 36] for a proof).

$$\begin{aligned} |\mathrm {Diag}\,S|\simeq |\overline{W}S|. \end{aligned}$$

(3)

2.2 Classifying spaces of 2-categories

In Quillen’s development of K-theory  [29], the higher K-groups are defined as the homotopy groups of a classifying space |C| associated to a (small) category C. This space is defined as

$$\begin{aligned} |C|=|{\mathrm {N}}C|, \end{aligned}$$

the geometric realization of the simplicial set termed its nerve

$$\begin{aligned} {\mathrm {N}}C: \Delta ^{\mathrm {op}}\rightarrow \mathbf {Set}, \ \ [p]\mapsto {\mathrm {N}}_pC=\coprod _{c_{0},\ldots ,c_p} C(c_{0},c_{1})\times C(c_{1},c_{2})\times \cdots \times C(c_{p-1},c_p), \end{aligned}$$

(4)

whose p-simplices are length p sequences of composable morphisms in C (${\mathrm {N}}_0 C=\mathrm {Ob}C$).

The classifying space $|\!|S|\!|$ of a simplicial category (that is, a simplicial object in $\mathbf {Cat}$) $S:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {Cat}$ is defined as the geometric realization of the bisimplicial set ${\mathrm {N}}S:\Delta ^{\!{\mathrm {op}}}\times \Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {Set}$, $([p],[q])\mapsto {\mathrm {N}}_qS_p$, obtained by composing S with the nerve functor ${\mathrm {N}}: \mathbf {Cat}\rightarrow \mathbf {SSet}$ from categories to simplicial sets. Thus, by (1), there is a natural homeomorphism

$$\begin{aligned} |\!|S |\!|=|\mathrm {Diag}{\mathrm {N}}S|\cong |[p]\mapsto |S_p||=|[p]\mapsto |[q]\mapsto {\mathrm {N}}_qS_p|| \end{aligned}$$

(5)

The notion of classifying space of a simplicial category provides the usual definition of the classifying space of a 2-category. Although for the general background on 2-categories used in this paper we refer to  [6, 33], to fix some notation and terminology, we shall recall that a 2-category C is just a category enriched in the category of small categories. Then, C is a category in which the hom-set between any two objects $c,c'\in C$ is the set of objects of a category $C(c,c')$, whose objects $p:c\rightarrow c'$ are called 1-cells and whose arrows are called 2-cells and are denoted by $\alpha :p\Rightarrow p'$ and depicted as

Composition in each category $C(c,c')$, usually referred to as the vertical composition of 2-cells, is denoted by $\alpha \cdot \beta$. Moreover, the horizontal composition is a functor

$$\begin{aligned} \mathcal {C}(c,c')\times \mathcal {C}(c',c'')\overset{\circ \ }{\rightarrow }\mathcal {C}(c,c'')((x,y)\mapsto y\circ x) \end{aligned}$$

that is associative and has identities $1_c\in \mathcal {C}(c,c)$.

For any 2-category C, the nerve construction (4) on it works by giving a simplicial category ${\mathrm {N}}C: \Delta ^{\mathrm {op}}\rightarrow \mathbf {Cat}$, whose classifying space is then the classifying space $|\!|C|\!|$ of the 2-category. Thus,

$$\begin{aligned} |\!|C|\!|= |\!|{\mathrm {N}}C|\!|=|\mathrm {Diag}{\mathrm {N}}{\mathrm {N}}C |\cong |[p]\mapsto |{\mathrm {N}}_p C|| \end{aligned}$$

(6)

(the double bar notation $|\!|$ avoids confusion with the classifying space |C| of the underlying category), where the bisimplicial set ${\mathrm {N}}{\mathrm {N}}C:\Delta ^{\!{\mathrm {op}}}\times \Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {Set}$, $([p],[q])\mapsto {\mathrm {N}}_q{\mathrm {N}}_p C$, is the double nerve of C.

The following fact will be used.

Fact 2.2

([14, Lemma 2.6]) If two 2-functors between 2-categories $F,G:A\rightarrow C$ are related by a lax or oplax transformation, $F\Rightarrow G$, then there is an induced homotopy, $|\!|F|\!|\Rightarrow |\!|G|\!|$, between the induced maps on classifying spaces $|\!|F|\!|,|\!|G|\!|:|\!|A|\!|\rightarrow |\!|C |\!|$.

The category $\mathbf {2}\mathbf {Cat}$ has a Thomason-type model structure, such that the classifying space functor $C \mapsto |\!|C|\!|$ is an equivalence of homotopy theories between 2-categories and topological spaces ([35, Theorem 4.5.1],  [1, Théorème 6.27]). Hereafter, we will always consider $\mathbf {2}\mathbf {Cat}$ with the Thomason model structure on it. Thus, for example, a 2-functor $F:A\rightarrow C$ is a weak equivalence if and only if the induced map $|\!|F|\!|:|\!|A|\!|\rightarrow |\!|C|\!|$ is a homotopy equivalence, and a commutative square of 2-categories and 2-functors

is a homotopy pullback if and only if the induced square on classifying spaces

is a homotopy pullback of spaces. Later, we shall use basic properties of homotopy pullbacks of spaces, such as the two out of three property, etc. (see  [17, Sect. 5] for instance). In particular, the homotopy-fibre characterization  [17, Sect. 5(2)], which easily leads us to assert that the square of 2-categories above is a homotopy pullback whenever, for any object $a\in A$, there is a commutative diagram of 2-categories and 2-functors

such that $a\in \mathrm {Im}F$, both the left square and the composite square are homotopy pullbacks, and $A'$ is weakly contractible ³ in the sense that the functor from $A'$ to the terminal (only one 2-cell) 2-category $A'\rightarrow \star$ is a weak equivalence, that is, if the classifying space $|\!|A'|\!|$ is contractible.

To conclude this preliminary section, we recall that the classifying space $|\!|\!|S|\!|\!|$ of a simplicial 2-category $S:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {2}\mathbf {Cat}$, is the geometric realization of the simplicial space obtained by composing S with the classifying space functor $|\!|\,\text {-}\,|\!|:\mathbf {2}\mathbf {Cat}\rightarrow \mathbf {Top}$. Therefore,

$$\begin{aligned} |\!|\!|S|\!|\!|=|[p]\mapsto |\!|S_p|\!||=|[p]\mapsto |\mathrm {Diag}{\mathrm {N}}{\mathrm {N}}S_p| |\cong |\mathrm {Diag}{\mathrm {N}}{\mathrm {N}}S|, \end{aligned}$$

(7)

where $\mathrm {Diag}{\mathrm {N}}{\mathrm {N}}S$ is the simplicial set, $[p]\mapsto {\mathrm {N}}_p{\mathrm {N}}_pS_p$, diagonal of the trisimplicial set ${\mathrm {N}}{\mathrm {N}}S$.

2.3 The Grothendieck construction on 2-functors

The so-called Grothendieck construction on diagrams of small categories underlies the 2-categorical construction we treat here for 2-diagrams of 2-categories. For a more general version of the Grothendieck construction below, which works even on lax bidiagrams of bicategories (in the sense of Benabou), we refer the reader to  [4, 9, 11–13].

We start by fixing some notations. Throughout the paper, the 2-category of (small) 2-categories, 2-functors, and 2-natural transformations is denoted by ${\underline{\mathbf{2Cat}}}$ (whereas $\mathbf {2Cat}$, recall, denotes its underlying category of 2-categories and 2-functors). We view any category as a 2-category in which all its 2-cells are identities, and thus ${\underline{\mathbf{Cat}}}$ $\subseteq$ ${\underline{\mathbf{2Cat}}}$ is the 2-subcategory consisting of categories, functors, and natural transformations.

Further, if C is a 2-category, the effect on cells of any 2-functor $\mathcal {D}:C \rightarrow$ ${\underline{\mathbf{2Cat}}}$ is denoted by

(8)

or, if $\mathcal {D}:C^{\mathrm {op}} \rightarrow$ ${\underline{\mathbf{2Cat}}}$ is contravariant, by

Let C be a 2-category, and let $\mathcal {D}:C \rightarrow$ ${\underline{\mathbf{2Cat}}}$ be a 2-functor. The Grothendieck construction on the 2-diagram $\mathcal {D}$ assembles the 2-diagram into a 2-category, denoted by

whose objects are pairs (a, x) with $a\in \mathrm {Ob}C$ and $x\in \mathrm {Ob}\mathcal {D}_{\!a}$, the 1-cells are pairs $(f,u):(a,x)\rightarrow (b,y)$, where $f:a\rightarrow b$ is a 1-cell in C and $u:f_*x\rightarrow y$ is a 1-cell in $\mathcal {D}_b$, and the 2-cells

are pairs consisting of a 2-cell of C together with a 2-cell $\phi :u\Rightarrow v\circ \alpha _*x$ in $\mathcal {D}_b$,

The vertical composition of 2-cells

is the 2-cell

$$\begin{aligned} (\beta ,\psi )\cdot (\alpha ,\phi )=(\beta \cdot \alpha , (\psi \circ 1_{\alpha _*x})\cdot \phi ):(f,u)\Rightarrow (h,w), \end{aligned}$$

and the identity 2-cell of a 1-cell (f, u) as above is $1_{(f,u)}=(1_f,1_u)$.

The horizontal composition of two 1-cells is the 1-cell

$$\begin{aligned} (f',u')\circ (f,u)=(f'\circ f, u'\circ f'_*u):(a,x)\longrightarrow (c,z), \end{aligned}$$

the identity 1-cell of an object (a, x) is $1_{(a,x)}=(1_a,1_x)$, and the horizontal composition of 2-cells

is the 2-cell

$$\begin{aligned} (\alpha ',\phi ')\circ (\alpha ,\phi )=(\alpha '\circ \alpha , \phi '\circ f'_*\phi ):(f'\circ f, u'\circ f'_*u) \Rightarrow (g'\circ g, v'\circ g'_*v). \end{aligned}$$

We denote by

(9)

the canonical projection 2-functor given on cells by forgetting the second components

Note that a 2-transformation $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ between 2-functors $\mathcal {D},\mathcal {E}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ induces the 2-functor $\int _C\Gamma : \int _C\mathcal {D}\rightarrow \int _C\mathcal {E}$ such that

Also, for $\Gamma ':\mathcal {D}\Rightarrow \mathcal {E}$ any other 2-transformation, a modification $m:\Gamma \Rrightarrow \Gamma '$ gives rise to the 2-transformation $\int _C m:\int _C \Gamma \Rightarrow \int _C \Gamma '$ given by

Thus, the 2-categorical Grothendieck construction provides a 2-functor

In a similar way, if $\mathcal {D}:C^{\mathrm {op}} \rightarrow$ ${\underline{\mathbf{2Cat}}}$ is a 2-functor, the Grothendieck construction on $\mathcal {D}$ is the 2-category, denoted by , whose objects are pairs (a, x) with $a\in \mathrm {Ob}C$ and $x\in \mathrm {Ob}\mathcal {D}_{\!a}$, whose 1-cells $(f,u):(a,x)\rightarrow (b,y)$ are pairs where $f:a\rightarrow b$ is a 1-cell in C and $u:x\rightarrow f^*y$ is a 1-cell in $\mathcal {D}_a$, and whose 2-cells $(\alpha ,\phi ):(u,f)\Rightarrow (v,g)$ are pairs consisting of a 2-cell $\alpha :u\Rightarrow v$ of C together with a 2-cell $\phi :\alpha ^*y\circ u\Rightarrow v$ in $\mathcal {D}_b$. As for the covariant case, the assignment $\mathcal {D}\mapsto \int _C\mathcal {D}$ is the function on objects of a 2-functor

2.4 The homotopy-fibre 2-functors

To finish this preliminary section, we review some needed results concerning the more striking examples of 2-diagrams of 2-categories: the 2-diagrams of homotopy-fibre 2-categories of a 2-functor.

As usual, if $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (resp. $\mathcal {D}:C^{\mathrm {op}} \rightarrow$ ${\underline{\mathbf{2Cat}}}$) and $F:A\rightarrow C$ are 2-functors, we denote by

$$\begin{aligned} F^*\mathcal {D}=\mathcal {D}\,F:A\rightarrow {\underline{\mathbf{2Cat}}} \end{aligned}$$

(resp. $F^*\mathcal {D}=\mathcal {D}\,F:A^{\mathrm {op}} \rightarrow$ ${\underline{\mathbf{2Cat}}}$) the 2-functor obtained by composing $\mathcal {D}$ with F.

Let $F:A\rightarrow C$ be any given 2-functor. Then, for any object $c\in C$, the homotopy-fibre of F over c  [14, 23], denoted by $F\!\downarrow \!c$, is the 2-category obtained by applying the Grothendieck construction on the 2-functor $F^*C(-,c):A^{\mathrm {op}}\rightarrow {\underline{\mathbf{Cat}}}$, where $C(-,c):C^{\mathrm {op}}\rightarrow {\underline{\mathbf{Cat}}}$ is the hom 2-functor; that is,

Thus, $F\!\downarrow \!c$ has objects the pairs (a, p), with a a 0-cell of A and $p:Fa\rightarrow c$ a 1-cell of C. A 1-cell $(u,\phi ):(a,p)\rightarrow (a',p')$ consists of a 1-cell $u:a\rightarrow a'$ in A, together with a 2-cell $\phi :p\Rightarrow p'\circ Fu$ in the 2-category C,

and, for $(u,\phi ),(u',\phi '):(a,p)\rightarrow (a',p')$, a 2-cell $\alpha :(u,\phi )\Rightarrow (u',\phi ')$ is a 2-cell $\alpha :u\Rightarrow u'$ in A such that $(1_{p'}\circ F\alpha )\cdot \phi =\phi '$. Compositions and identities are given canonically.

Any 1-cell $h:c\rightarrow c'$ in C gives rise to a 2-functor

$$\begin{aligned} h_*:F\!\downarrow \!c \rightarrow F\!\downarrow \!c', \end{aligned}$$

which acts on cells by

and, for $h,h':c\rightarrow c'$, any 2-cell $\psi :h\Rightarrow h'$ in C produces a 2-transformation

$$\begin{aligned} \psi _*:h_*\Rightarrow h'_*, \end{aligned}$$

whose component at any object (a, p) of $F\!\downarrow \!c$ is the 1-cell of $F\!\downarrow \!c'$

$$\begin{aligned} \psi _*(a,p)= (1_a,\psi \circ 1_p):(a,h\circ p)\rightarrow (a,h'\circ p). \end{aligned}$$

In this way, we have the homotopy-fibre 2-functor

where $\mathcal {Y}$ is the 2-categorical Yoneda embedding; and, quite similarly, we also have the homotopy-fibre 2-functor

which assigns to each object c of C the homotopy-fibre 2-category of F under c, $c\!\downarrow \!F$, whose objects are pairs $(a,c\overset{p}{\rightarrow }Fa)$. The 1-cells $(u,\phi ):(a,p)\rightarrow (a',p')$ are pairs where $u:a\rightarrow a'$ is a 1-cell of A and $\phi :Fu\circ p\Rightarrow p'$ is a 2-cell of C, and a 2-cell $\alpha :(u,\phi )\Rightarrow (u',\phi ')$ is a 2-cell $\alpha :u\Rightarrow u'$ in A such that $\phi '\cdot (F\alpha \circ 1_p)=\phi$.

In the particular case where $F=1_C$ is the identity 2-functor on C, we have the comma 2-categories $C\!\downarrow \!c$, of objects over an object c, and $c\!\downarrow \!C$, of objects under c. The following fact is proved in  [10, Theorem 4.1]:

Lemma 2.1

For any 2-category C and any object $c\in C$, the 2-categories $c\!\downarrow \!C$ and $C\!\downarrow \!c$ are weakly contractible.

Returning to an arbitrary 2-functor $F:A\rightarrow C$, the 2-diagrams $F\!\downarrow \!-$ and $-\!\downarrow \!F$ are relevant for homotopy interests, mainly because Quillen’s Theorem B in  [29] has also been generalized for 2-functors between 2-categories as in Theorem 2.3 below. We shall first set some terminology. Following Dwyer, Kan, and Smith in  [21, Sect. 6] and Barwick and Kan in  [5], we say that:

• F has the property B$_l$ if, for any 1-cell $h:c\rightarrow c'$ in C, the induced 2-functor $h_*:F\!\downarrow \! c \rightarrow F\!\downarrow \! c'$ is a weak equivalence,⁴

• F has the property B$_r$ if, for any 1-cell $h:c\rightarrow c'$ in C, the induced 2-functor $h^*:c'\!\downarrow \! F \rightarrow c\!\downarrow \!F$ is a weak equivalence.

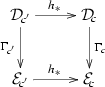
Now, observe that, for any object c of C, there are two pullback squares in ${\mathbf {2}\mathbf {Cat}}$

(10)

where the vertical 2-functors $\pi$ are the canonical projections (9), and both 2-functors $\bar{F}$ act on cells by

Then, the extension of Quillen’s Theorem B for 2-functors in  [14, Theorem 3.2] tells us that the following theorem holds.

Theorem 2.3

A 2-functor $F : A\rightarrow C$ has the property $\mathrm {B}_l$ (resp. $\mathrm {B}_r$) if and only if the left (resp. right) square in (10) is a homotopy pullback for every object $c\in C$.

As an interesting consequence, we have the 2-categorical version of Quillen’s Theorem A in  [29] in Theorem 2.4 below. First, let us borrow some terminology from Hirschhorn in  [26, 19.6.1]:

• a 2-functor $F:A\rightarrow C$ is called homotopy left cofinal if all the homotopy-fibre 2-categories $F\!\downarrow \!c$, $c\in C$, are weakly contractible,⁵

• a 2-functor $F:A\rightarrow C$ is called homotopy right cofinal if all the homotopy-fibre 2-categories $c\!\downarrow \!F$, $c\in C$, are weakly contractible.

Since every homotopy left (resp. right) cofinal 2-functor has the property $\mathrm {B}_l$ (resp. $\mathrm {B}_r$), from Theorem 2.3, it follows the following extension of Quillen’s Theorem A, which was originally proved in  [10, Theorem 1.2].

Theorem 2.4

Every homotopy left or right cofinal 2-functor between 2-categories is a weak equivalence.

3 The homotopy colimit and homotopy invariance theorems

As we said in the introduction, the goal of this paper is to state and prove the more relevant homotopy properties of the Grothendieck construction on 2-diagrams of 2-categories. Most of this section is dedicated to proving Theorem 3.1 below, which has Thomason’s homotopy colimit theorem  [34, Theorem 1.2] as its natural precedent and also includes the results in  [14, Theorem 4.5] as particular cases. The result therein, on which many further results are based, states that, for any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the classifying space of the 2-category $\int _{C}\mathcal {D}$ can be realized, up to homotopy equivalence, through the simplicial bar construction on $\mathcal {D}$, also called Borel construction, or simplicial replacement, denoted by $\mathcal {B}_C\mathcal {D}$ and defined as follows.⁶

Definition 3.1

Let C be a 2-category and $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ be a 2-functor. The simplicial bar construction on $\mathcal {D}$ is the simplicial 2-category

$$\begin{aligned} \mathcal {B}_C\mathcal {D}:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {2}\mathbf {Cat}, \end{aligned}$$

(11)

whose 2-category of p-simplices is

$$\begin{aligned} \mathcal {B}_C\mathcal {D}_p= \coprod _{c_0,\ldots ,c_p} \mathcal {D}_{\!c_0}\!\times C(c_0,c_1)\times C(c_1,c_2)\times \cdots \times C(c_{p-1},c_p), \end{aligned}$$

and whose face and degeneracy 2-functors are defined as follows: The face 2-functor $d_0$ is induced by the 2-functor

$$\begin{aligned} d_0: \mathcal {D}_{\!c_0}\times C(c_0,c_1)\rightarrow \mathcal {D}_{\!c_1}, \end{aligned}$$

which carries an object $(x,c_0\overset{f}{\rightarrow }c_1)$ to the object $f_*x$. A 1-cell $(u,\alpha ):(x,f)\rightarrow (y,g)$ is carried by $d_0$ to the composite 1-cell $g_*u\circ \alpha _*x:f_*x\rightarrow g_*y$,

and $d_0$ acts on 2-cells by

The other face and degeneracy 2-functors are induced by the operators $d_i$ and $s_i$ in ${\mathrm {N}}C$ as $1_{\!\mathcal {D}_{\!c_0}}\!\times d_i$ and $1_{\!\mathcal {D}_{\!c_0}}\!\times s_i$, respectively.

It is not hard to see that, if $\mathcal {D},\mathcal {E}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ are 2-functors, then any 2-transformation $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ gives rise to a simplicial functor $\Gamma _*:\mathcal {B}_C\mathcal {D}\rightarrow \mathcal {B}_C\mathcal {E}$; and also that a modification $m:\Gamma \Rrightarrow \Gamma '$, where $\Gamma ':\mathcal {D}\Rightarrow \mathcal {E}$ is any other 2-transformation, induces a simplicial transformation $m_*:\Gamma _*\Rightarrow \Gamma '_*$. Thus, the simplicial bar construction provides a 2-functor

$$\begin{aligned} \mathcal {B}_C-:{\underline{\mathbf{2Cat}}}^C \rightarrow \underline{\mathbf {2}\mathbf {Cat}}^{\Delta ^{\mathrm {op}}}. \end{aligned}$$

There is an analogous construction $\mathcal {B}_C\mathcal {D}$ for contravariant 2-functors $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$. This is as follows:⁷ We call the simplicial bar construction on $\mathcal {D}$ the simplicial 2-category

$$\begin{aligned} \mathcal {B}_C\mathcal {D}:\Delta ^{\!{\mathrm {op}}}\rightarrow \mathbf {2}\mathbf {Cat}\end{aligned}$$

(12)

whose 2-category of p-simplices is

$$\begin{aligned} \mathcal {B}_C\mathcal {D}_p= \coprod _{c_0,\ldots ,c_p} C(c_0,c_1)\times C(c_1,c_2)\times \cdots \times C(c_{p-1},c_p)\times \mathcal {D}_{\!c_p} \end{aligned}$$

and whose faces and degeneracies are induced by the corresponding ones in ${\mathrm {N}}C$, as $d_i\times 1_{\!\mathcal {D}_{\!c_p}}$ and $s_i\times 1_{\!\mathcal {D}_{\!c_p}}$, for $0\le i<p$, whereas the face 2-functor $d_p$ is induced by the 2-functor

$$\begin{aligned} d_p: C(c_{p-1},c_p)\times \mathcal {D}_{\!c_p}\rightarrow \mathcal {D}_{\!c_{p-1}}, \end{aligned}$$

which acts on cells by

Thus, the construction $\mathcal {D}\mapsto \mathcal {B}_C\mathcal {D}$ is the function on objects of a 2-functor

$$\begin{aligned} \mathcal {B}_C-:{\underline{\mathbf{2Cat}}}^{C^{\mathrm {op}}} \rightarrow {\underline{\mathbf{2Cat}}}^{\Delta ^{\mathrm {op}}}. \end{aligned}$$

Theorem 3.1

(The homotopy colimit theorem) For any 2-functor $\mathcal {D}: C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (or $\mathcal {D}: C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$), where C is a 2-category, there exists a natural homotopy equivalence

Proof

We shall treat only the covariant case, as the other is proven similarly. The strategy of the proof is as follows: For any given 2-functor $\mathcal {D}: C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, we build a trisimplicial set $E=E(\mathcal {D})$, together with isomorphisms of simplicial sets

$$\begin{aligned} {\overline{W}}([p]\mapsto \mathrm {Diag}E_{p,\bullet ,\bullet })&\cong {\overline{W}}([p]\mapsto {\overline{W}}{\mathrm {N}}{\mathrm {N}}\mathcal {B}_C\mathcal {D}_p), \end{aligned}$$

(13)

(14)

so that, by Fact 2.1 and (3), we have a homotopy equivalence

As $|\!|\int _{C}\mathcal {D}|\!|=|\mathrm {Diag}{\mathrm {N}}{\mathrm {N}}\int _{C}\mathcal {D}|\overset{(3)}{\simeq }|{\overline{W}}{\mathrm {N}}{\mathrm {N}}\int _{C}\mathcal {D}|$, while

$$\begin{aligned} |\!|\!|\mathcal {B}_C\mathcal {D}|\!|\!|&\overset{(7)}{=}|\mathrm {Diag}{\mathrm {N}}{\mathrm {N}}\mathcal {B}_C\mathcal {D}|= |\mathrm {Diag}\big ([p]\mapsto \mathrm {Diag}{\mathrm {N}}{\mathrm {N}}\mathcal {B}_C\mathcal {D}_p\big )|\\&\!\!\!\!\overset{(3), \text{ Fact } \text{2.1 }}{\simeq }|\mathrm {Diag}\big ([p]\mapsto {\overline{W}}{\mathrm {N}}{\mathrm {N}}\mathcal {B}_C\mathcal {D}_p\big )|\overset{(3)}{\simeq }|{\overline{W}}([p]\mapsto {\overline{W}}{\mathrm {N}}{\mathrm {N}}\mathcal {B}_C\mathcal {D}_p)|, \end{aligned}$$

the proof will be complete.

Before starting the construction of E, we shall describe, for any 2-category, C say, the simplicial set ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$. To do that, let us first represent a (p, q)-simplex of the bisimplicial set ${\mathrm {N}}{\mathrm {N}}C$ as a diagram $(c,f,\alpha )_{p,q}$ in C of the form

(15)

whose horizontal i-face is obtained by deleting the object $c_{q+i}$ and using, for $0<i<p$, the composite cells $f^k_{q+i+1}\circ f^k_{q+i}$ and $\alpha ^k_{q+i+1}\circ \alpha ^k_{q+i}$ to rebuild the new $(p-1,q)$-simplex, and whose vertical j-face is obtained by deleting all the 1-cells $f^j_{q+m}$ and using the composite 2-cells $\alpha ^{j+1}_{q+m}\cdot \alpha ^{j}_{q+m}$, for $0<j<q$, to complete the $(p,q-1)$ simplex of ${\mathrm {N}}{\mathrm {N}}B$. Then, it is straightforward to obtain the following description of the simplicial set ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$: The vertices are the objects $c_0$ of C, the 1-simplices are the 1-cells $f_1^0:c_0\rightarrow c_1$ of C, and, for $n\ge 2$, the n-simplices are diagrams $(c,f,\alpha )_n$ in C of the form

(16)

that is, they consist of objects $c_m$ of C, $0\le m\le n$, 1-cells $f_m^k:c_{m-1}\rightarrow c_{m}$, $0\le k <m\le n$, and 2-cells $\alpha _m^k:f_m^{k-1}\Rightarrow f_m^{k}$, $0<k<m\le n$. The simplicial operators of ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$ act much as for the usual nerve of an ordinary category: The i-face of an n-simplex as in (16) is obtained by deleting the object $c_i$ and the 1-cells $f_m^{i}:c_{m-1}\rightarrow c_m$, for $i< m$, and using the composite 1-cells $f^k_{i+1}\circ f^k_i:c_{i-1}\rightarrow c_{i+1}$, $k<i$, the horizontally composite 2-cells $\alpha ^k_{i+1}\circ \alpha ^k_i:f^{k-1}_{i+1}\circ f^{k-1}_i\Rightarrow f^k_{i+1}\circ f^k_i$, $0<k<i$, and the vertically composed 2-cells $\alpha ^{i+1}_m\cdot \alpha ^i_m:f^{i-1}_m\Rightarrow f^{i+1}_m$, when $i<m-1$, to complete the new $(n-1)$-simplex. The i-degeneracy of $(c,f,\alpha )_n$ is constructed by repeating the object $c_i$ at the $i + 1$-place and inserting $i+1$ times the identity 1-cell $1_{c_i}:c_i\rightarrow c_i$, i times the identity 2-cell $1_{1_{c_i}}:1_{c_i}\Rightarrow 1_{c_i}$ and, for each $i<m$, by replacing the 1-cell $f_m^i:c_{m-1}\rightarrow c_m$ by the identity 2-cell $1_{f_m^i}:f_m^i\Rightarrow f_m^i$.

Then, the simplicial set ${\overline{W}}([p]\mapsto {\overline{W}}{\mathrm {N}}{\mathrm {N}}\mathcal {B}_C\mathcal {D}_p)$ can be described as follows: Its n-simplices are pairs

$$\begin{aligned} ((c,f,\alpha )_n,(x,u,\phi )_n) \end{aligned}$$

(17)

where $(c,f,\alpha )_n$ is an n-simplex of ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$ as in (16), whereas $(x,u,\phi )_n$ is a list with a diagram in each 2-category $\mathcal {D}_{\!c_0}$,...,$\mathcal {D}_{\!c_n}$ of the form

(18)

That is, $(x,u,\phi )_n$ consists of 0-cells $x_k$ of $\mathcal {D}_{\!c_k}$, $0\le k\le n$, 1-cells $u_m^k:f^{m-1}_{m*}x_{m-1}\rightarrow x_{m}$, $0\le k <m\le n$, and 2-cells $\phi _m^k:u_m^{k-1}\Rightarrow u_m^{k}$, $0<k<m\le n$. Further, the i-face of the simplex $((c,f,\alpha )_n,(x,u,\phi )_n)$ is obtained by taking the i-face of $(c,f,\alpha )_n$ in the simplicial set ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$ and, in a similar way, by deleting the object $x_i$ and the 1-cells $u_m^{i}:f_{m*}^{m-1}x_{m-1}\rightarrow x_m$, for $i< m$, and then using the composite 1-cells

for $k<i$, the horizontally composite 2-cells

for $0<k<i$, and the vertically composed 2-cells $\phi ^{i+1}_m\cdot \phi ^i_m:u^{i-1}_m\Rightarrow u^{i+1}_m$, $i<m-1$, to complete the new $(n-1)$-simplex. Similarly, the i-degeneracy of $((c,f,\alpha )_n,(x,u,\phi )_n)$ is given by first taking the i-degeneracy of $(c,f,\alpha )_n$ in the simplicial set ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$ and second by repeating the object $x_i$, inserting $i+1$ times the identity 1-cell $1_{x_i}:x_i\rightarrow x_i$, i times the identity 2-cell $1_{1_{x_i}}:1_{x_i}\Rightarrow 1_{x_i}$ and, for each $i<m$, by replacing the 1-cell $u_m^{i}$ by the identity 2-cell $1_{u_m^i}:u_m^i\Rightarrow u_m^i$.

Now we construct $E=E(\mathcal {D})$ as the trisimplicial set whose (p, n, q)-simplices are pairs

$$\begin{aligned} ((c,f,\alpha )_{p,q},(x,u,\phi )_{p,n,q}) \end{aligned}$$

(19)

with $(c,f,\alpha )_{p,q}$ a (p, q)-simplex of ${\mathrm {N}}{\mathrm {N}}C$, as in (15), and $(x,u,\phi )_{p,n,q}$ a system of data consisting of a diagram in each 2-category $\mathcal {D}_{\!c_{q+1}}$, ..., $\mathcal {D}_{\!c_{q+p}}$ of the form

That is, it consists of objects $x_{q}\in D_{\!c_q}$, $\ldots$, $x_{q+p}\in \mathcal {D}_{\!c_{q+p}}$, 1-cells $u^k_{q+m}:f^q_{q+m*}x_{q+m-1}\rightarrow x_{q+m}$, $0\le k\le n$, $0< m\le p$, and 2-cells $\phi ^k_{q+m}:u^{k-1}_{q+m}\Rightarrow u^{k}_{q+m}$, $0< k\le n$, $0< m\le p$.

The i-face in the p-direction map of E carries the (p, n, q)-simplex (20) to the $(p-1,n,q)$-simplex obtained by taking the horizontal i-face of $(c,f,\alpha )_{p,q}$ in ${\mathrm {N}}{\mathrm {N}}C$, deleting the object $x_{q+i}$, and using the composite 1-cells

and the horizontally composite 2-cells

to complete the new $(p-1,n,q)$-simplex.

The j-face in the n-direction of the (p, n, q)-simplex (20) is obtained by keeping $(c,f,\alpha )_{p,q}$ unaltered, deleting all the 1-cells $u^j_{q+m}$, and using, when $0<j<n$, the composite 2-cells $\phi ^{j+1}_{q+m}\cdot \phi ^{j}_{q+m}$ to complete the simplex.

For any $k<q$, the k-face in the q-direction of the (p, n, q)-simplex (20) is given by replacing $(c,f,\alpha )_{p,q}$ by its vertical k-face in ${\mathrm {N}}{\mathrm {N}}C$ and keeping $(x,u,\phi )_{p,n,q}$ unchanged, while its q-face consists of the vertical q-face of $(c,f,\alpha )_{p,q}$ in ${\mathrm {N}}{\mathrm {N}}C$ (which, recall, is obtained by deleting the 1-cells $f^q_{q+m}$) together with the list of diagrams

With degeneracies given in a standard way, it is straightforward to see that E is a trisimplicial set. Then, an easy verification shows that the isomorphisms in (13),

$$\begin{aligned} {\overline{W}}([p]\mapsto \mathrm {Diag}E_{p,\bullet ,\bullet })\cong {\overline{W}}([p]\mapsto {\overline{W}}{\mathrm {N}}{\mathrm {N}}\mathcal {B}_C\mathcal {D}_p), \end{aligned}$$

holds.

Now, an analysis of the simplicial set ${\overline{W}}E_{p,\bullet ,\bullet }$ says that its q-simplices are pairs

$$\begin{aligned} ((c,f,\alpha )_{p,q},(x,u,\phi )_{p,q}) \end{aligned}$$

(20)

with a (p, q)-simplex $(c,f,\alpha )_{p,q}$ of ${\mathrm {N}}{\mathrm {N}}C$, as in (15), together with data $(x,u,\phi )_{p,q}$ consisting of a diagram in each 2-category $\mathcal {D}_{\!c_{q+1}}$, ..., $\mathcal {D}_{\!c_{q+p}}$ of the form

More precisely, $(x,u,\phi )_{p,q}$ consists of objects

$$\begin{aligned} x_{q}\in \mathcal {D}_{\!c_q}, \ldots , x_{q+p}\in \mathcal {D}_{\!c_{q+p}}, \end{aligned}$$

1-cells

$$\begin{aligned} u^k_{q+m}:f^k_{q+m*}x_{q+m-1}\rightarrow x_{q+m}, (0\le k\le q,\, 0< m\le p) \end{aligned}$$

and 2-cells

$$\begin{aligned} \phi ^k_{q+m}:u^{k-1}_{q+m}\Rightarrow u^{k}_{q+m}\circ \alpha ^k_{q+m*}x_{q+m-1} (0< k\le n,\, 0< m\le p). \end{aligned}$$

The j-face of such a q-simplex (20) is given by taking the vertical j-face of $(c,f,\alpha )_{p,q}$ in ${\mathrm {N}}{\mathrm {N}}C$, deleting the 1-cells $u^j_{q+m}$, and inserting the pasted 2-cells below, for $0<j<q$.

Then, an easy and straightforward verification shows that an n-simplex of the simplicial set ${\overline{W}}([p]\mapsto {\overline{W}}E_{p,\bullet ,\bullet })$ is a pair

$$\begin{aligned} ((c,f,\alpha )_n,(x,u,\phi )_n), \end{aligned}$$

(21)

where $(c,f,\alpha )_n$ is an n-simplex of ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$ as in (16), while $(x,u,\phi )_n$ is a list with a diagram in each 2-category $\mathcal {D}_{\!c_0}$,...,$\mathcal {D}_{\!c_n}$ of the form

That is, $(x,u,\phi )_n$ consists of 0-cells

$$\begin{aligned} x_{0}\in \mathcal {D}_{\!c_0}, \ldots , x_{n}\in \mathcal {D}_{\!c_{n}}, \end{aligned}$$

1-cells

$$\begin{aligned} u^k_{m}:f^k_{m*}x_{m-1}\rightarrow x_{m}, (0\le k<m\le n) \end{aligned}$$

and 2-cells

$$\begin{aligned} \phi ^k_{m}:u^{k-1}_{m}\Rightarrow u^{k}_{m}\circ \alpha ^k_{m*}x_{m-1} (0<k<m\le n). \end{aligned}$$

Further, the i-face of the simplex $((c,f,\alpha )_n,(x,u,\phi )_n)$ is obtained by taking the i-face of $(c,f,\alpha )_n$ in the simplicial set ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$ and, in a similar way, by deleting the object $x_i$ and all the 1-cells $u_m^{i}:f_{m*}^{i}x_{m-1}\rightarrow x_m$, for $i< m$, and then using the composite 1-cells

for $k<i$, and the pasted 2-cells

for $0<k<i$, and

for $0<i<m-1$, to complete the i-face $(n-1)$ simplex. Similarly, the i-degeneracy of $((c,f,\alpha )_n,(x,u,\phi )_n)$ is given by first taking the i-degeneracy of $(c,f,\alpha )_n$ in the simplicial set ${\overline{W}}{\mathrm {N}}{\mathrm {N}}C$ and secondly by repeating the object $x_i$, inserting $i+1$ times the identity 1-cell $1_{x_i}:x_i\rightarrow x_i$, i times the identity 2-cell $1_{1_{x_i}}:1_{x_i}\Rightarrow 1_{x_i}$ and, for each $i<m$, by repeating the 1-cell $u_m^{i}:f^i_{m*}x_{i-1}\rightarrow x_i$ and inserting the identity 2-cell $1_{u_m^i}:u_m^i\Rightarrow u_m^i$.

Finally, observe that any n-simplex $((c,f,\alpha )_n,(x,u,\phi )_n)$ of ${\overline{W}}([p]\mapsto {\overline{W}}E_{p,\bullet ,\bullet })$, such as (21), identifies with the n-simplex $((c,x),(f,u),(\alpha ,\phi ))_n \in {\overline{W}}{\mathrm {N}}{\mathrm {N}}\int _{C}\mathcal {D}$,

given by the objects $(c_m,x_m)$ of $\int _C\mathcal {D}$, $0\le m\le n$, the 1-cells

$$\begin{aligned} (f^k_m,u_m^k):(c_{m-1},x_{m-1})\rightarrow (c_m,x_{m}), (0\le k <m\le n), \end{aligned}$$

and 2-cells

$$\begin{aligned} (\alpha ^k_m,\phi _m^k):(f^{k-1}_m,u_m^{k-1})\Rightarrow (f^k_m,u_m^{k})(0<k<m\le n). \end{aligned}$$

Thus, the claimed simplicial isomorphism in (14) holds. $\square$

The first basic property below quickly follows from Theorem 3.1.

Theorem 3.2

(Homotopy Invariance Theorem) Let $\mathcal {D},\mathcal {E}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (or $\mathcal {D},\mathcal {E}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$) be 2-functors, where C is any 2-category. If $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ is a 2-transformation such that, for each object c of C, the 2-functor $\Gamma _c:\mathcal {D}_c\rightarrow \mathcal {E}_c$ is a weak equivalence of 2-categories, then the induced map on classifying spaces

is a homotopy equivalence.

Proof

By Theorem 3.1, we can argue with $\mathcal {B}_C-$ instead of $\int _\mathcal {C}-$. Since $\Gamma$ is objectwise a weak equivalence, for any integer $p\ge 0$ the induced 2-functor $\mathcal {B}_C\mathcal {D}_p\rightarrow \mathcal {B}_C\mathcal {E}_p$,

$$\begin{aligned}&\coprod _{c_0,\ldots ,c_p} \mathcal {D}_{\!c_0}\!\times C(c_0,c_1)\times \cdots \times C(c_{p-1},c_p) \\&\quad \longrightarrow \coprod _{c_0,\ldots ,c_p} \mathcal {E}_{c_0}\!\times C(c_0,c_1)\times \cdots \times C(c_{p-1},c_p), \end{aligned}$$

is a weak equivalence. Then, by Fact 2.1, $|\!|\!|\mathcal {B}_C\mathcal {D}|\!|\!|=|[p]\mapsto |\!|\mathcal {B}_C\mathcal {D}_p|\!|| \simeq |[p]\mapsto |\!|\mathcal {B}_C\mathcal {E}_p|\!||= |\!|\!|\mathcal {B}_C\mathcal {E}|\!|\!|$. $\square$

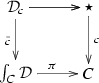
If $\mathrm {Ct}D:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ denote the constant 2-functor on a 2-category C given by a 2-category D, then the Grothendieck construction on it just gives the product 2-category of C and D, that is,

In particular, for $D=\star$ the terminal 2-category, $\int _C\,\mathrm {Ct}\star =C\times \star \cong C$. We use this elemental observation in the proof of the following corollary.

Corollary 3.1

Let C be a 2-category and $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (or $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$) a 2-functor such that, for any object c of C, the 2-category $\mathcal {D}_{\!c}$ is weakly contractible. Then, the projection 2-functor (9), $\pi : \int _C\mathcal {D}\rightarrow C$, is a weak equivalence.

Proof

By Theorem 3.2, the induced 2-functor by the collapse 2-transformation $\mathcal {D}\Rightarrow \mathrm {Ct}\star$, $\int _C\mathcal {D}\rightarrow \int _C\,\mathrm {Ct}\star$ is a weak equivalence. As the projection 2-functor $\pi$ is the composite $\int _C\mathcal {D}\rightarrow \int _C\,\mathrm {Ct}\star =C\times \star \cong C$, the result follows. $\square$

4 Theorems A and B

In this section, we state and prove extensions of Theorems 2.3 and 2.4 for 2-transformations between 2-diagrams of 2-categories.

For any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (or $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$) and any object $c\in C$, let

denote the embedding 2-functor

If $\mathcal {D},\,\mathcal {E}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ are 2-functors and $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ is a 2-transformation, for any objects $c\in C$ and $y\in \mathcal {E}_c$, there is a canonical commutative square of 2-categories

(22)

which, keeping the notations in squares (10), is the composite of the squares

and we have the theorem below.

Theorem 4.1

(Theorem $\mathrm {B}_l$ for 2-transformations) Let $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ be a 2-transformation, where $\mathcal {D},\,\mathcal {E}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ are 2-functors. The following properties are equivalent:

• (a) For any object c in C and any object y in $\mathcal {E}_c$, the square (22) is a homotopy pullback.

• (b) The 2-functor $\int _C\Gamma :\int _C\mathcal {D}\rightarrow \int _C\mathcal {E}$ has the property $\mathrm {B}_l$.

• (c) The two conditions below hold.

  • $\mathrm {B1}_l$: For each object c of C, the 2-functor $\Gamma _c:\mathcal {D}_c\rightarrow \mathcal {E}_c$ has the property $\mathrm {B}_l$.

  • $\mathrm {B2}_l$: For each 1-cell $h:c\rightarrow c'$ in C and any object $y\in \mathcal {E}_c$, the induced 2-functor

    

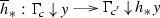
    is a weak equivalence.

• (d) The two conditions below hold.

  • $\mathrm {B1}_l$  For each object c of C, the 2-functor $\Gamma _c:\mathcal {D}_c\rightarrow \mathcal {E}_c$ has the property $\mathrm {B}_l$.

  • $\mathrm {B2}'_l$  For each 1-cell $h:c\rightarrow c'$ in C, the square

    

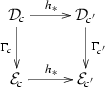    (23)

    is a homotopy pullback.

Proof

In order to prove the result, first we show that, for any object c in C and any object y in $\mathcal {E}_c$, there is a weak equivalence

(24)

Here, R is the 2-functor acting on cells of the 2-category $\int _C\!\Gamma \! \downarrow \!(c,y)$ in the following way: On objects ((a, x), (p, v)), where a is an object of C, x an object of $\mathcal {D}_a$, $p:a\rightarrow c$ is a 1-cell in C, and $v:p_*\Gamma _{\!a}x=\Gamma _{\!c}p_*x\rightarrow y$ is a 1-cell in $\mathcal {E}_c$,

$$\begin{aligned} R((a,x),(p,v))=(p_*x,v). \end{aligned}$$

On 1-cells

$$\begin{aligned} ((f,u),(\alpha ,\psi )):((a,x),(p,v))\rightarrow ((a',x'),(p',v')), \end{aligned}$$

(25)

where $f:a\rightarrow a'$ is in C, $u:f_*x\rightarrow x'$ in $\mathcal {D}_a$, $\alpha :p\Rightarrow p'\circ f$ in C, and $\psi :v\Rightarrow v'\circ p'_*\Gamma _{\!a'}u\circ \alpha _*\Gamma _{\!a}x$ in $\mathcal {E}_c$,

$$\begin{aligned} R((f,u),(\alpha ,\psi ))=(p'_*u\circ \alpha _*x,\psi ):(p_*x,v)\rightarrow (p'_*x',v'). \end{aligned}$$

And, for a 2-cell $(\beta ,\phi ):((f,u),(\alpha ,\psi ))\Rightarrow ((f',u'),(\alpha ',\psi '))$, where $\beta :f\Rightarrow f'$ is in C and $\phi :u\Rightarrow u'\circ \beta _*x$ in $\mathcal {D}_a$, satisfying the corresponding conditions,

$$\begin{aligned} R(\beta ,\phi )=p'_*\phi \circ 1_{\alpha _*x}:(p'_*u\circ \alpha _*x,\psi )\Rightarrow (p'_*u'\circ \alpha '_*x,\psi '). \end{aligned}$$

This 2-functor R is actually a retraction, with a section given by the induced 2-functor on homotopy-fibre 2-categories

(26)

making the diagram below commutative:

Explicitly, $\bar{c}$ in (26) acts on objects (x, v), where x is an object of $\mathcal {D}_c$ and $v:\Gamma _{\!c}x\rightarrow y$ is a 1-cell of $\mathcal {E}_c$, by

$$\begin{aligned} \bar{c}(x,v)=((c,x),(1_c,v)), \end{aligned}$$

on 1-cells $(u,\psi ):(x,v)\rightarrow (x',v')$, where $u:x\rightarrow x'$ is in $\mathcal {D}_c$ and $\psi :v\Rightarrow v'\circ \Gamma _{\!c}u$ in $\mathcal {E}_c$, by

$$\begin{aligned} \bar{c}(u,\psi )=((1_c,u),(1_{1_c},\psi )):((c,x),(1_c,v))\rightarrow ((c,x'),(1_c,v')), \end{aligned}$$

and, on a 2-cell $\phi :(u,\psi )\Rightarrow (u',\psi ')$,

$$\begin{aligned} \bar{c}(\phi )=(1_{1_c},\phi ):((1_c,u),(1_{1_c},\psi ))\Rightarrow ((1_c,u'),(1_{1_c},\psi ')). \end{aligned}$$

It is plain to see that $R\,\bar{c}=1$. Furthermore, there is an oplax transformation $1\Rightarrow \bar{c}\,R$ given, on any object ((a, x), (p, v)) of $\int _C\!\Gamma \! \downarrow \!(c,y)$, by the 1-cell

$$\begin{aligned} ((p,1_{p_*x}),(1_p,1_v)): ((a,x),(p,v))\rightarrow ((c,p_*x),(1_c,v)), \end{aligned}$$

and whose naturality component at any 1-cell as in (25) is

Hence, for the maps induced by R and $\bar{c}$ on classifying spaces, we have $|\!|R|\!|\,|\!|\bar{c}|\!|=1$ and, by Fact 2.2, $1\simeq |\!|\bar{c}|\!|\,|\!|R|\!|$. Thus, it follows that both 2-functors R and $\bar{c}$ are weak equivalences.

Let us now observe that the square (22) is the composite of the squares

Therefore, as both vertical 2-functors $\bar{c}$ are weak equivalences, the square (22) is a homotopy pullback if and only if the square (I) above is as well. Thus, by Theorem 2.3, it follows that $(a)\Leftrightarrow (b)$.

To prove $(b)\Leftrightarrow (c)$, let us observe that, for any 1-cell $(h,w):(c,y)\rightarrow (c',y')$ in $\int _C\mathcal {E}$, there is a commutative diagram of 2-functors

where both vertical 2-functors R are weak equivalences. If the 2-transformation $\Gamma$ has the properties $\mathrm {B1}_l$ and $\mathrm {B2}_l$, then both 2-functors $\bar{h}_*$ and $w_*$ in the bottom of the diagram above are weak equivalences, and therefore the 2-functor $\overline{(h,w)}_*$ at the top is also a weak equivalence. That is, the 2-functor $\int _C\Gamma$ has the property $\mathrm {B}_l$.

Conversely, assume that $\int _C\Gamma$ has the property $\mathrm {B}_l$. Then, for any object c of C and any 1-cell $w:y\rightarrow y'$ of $\mathcal {E}_c$, the above commutative square for the case where $h=1_c$ proves that the 2-functor $w_*:\Gamma _{\!c}\!\downarrow \!y\rightarrow \Gamma _{\!c}\!\downarrow \!y'$ is a weak equivalence; that is, $\Gamma _{\!c}:\mathcal {D}_c\rightarrow \mathcal {E}_c$ has the property $\mathrm {B}_l$. Similarly, the commutativity of the above square for $w=1_y$ implies that, for every 1-cell $h:c\rightarrow c'$ on C and any object $y\in \mathcal {E}_c$, the 2-functor $\bar{h}_*:\Gamma _{\!c}\!\downarrow \!y\rightarrow \Gamma _{\!c'}\!\downarrow \!h_*y$ is a weak equivalence.

Finally, the equivalence $(c)\Leftrightarrow (d)$ is consequence of the homotopy fibre characterization of homotopy pullbacks of spaces (hence of 2-categories, see Sect. 2.2): For any 1-cell $h:c\rightarrow c'$ in C and any object $y\in \mathcal {E}_c$, we have the equality of composite squares $(I)+(II)=(III)+(IV)$, where

Under the hypothesis $\mathrm {B1}_l$, the squares (I) and (IV) are both homotopy pullbacks (where, recall, the comma 2-categories $\mathcal {E}_{\!c}\!\downarrow \!y$ and $\mathcal {E}_{\!c'}\!\downarrow \!h_*y$ are weakly contractible). Then, as the square $(II)=(23)$ is a homotopy pullback if and only if, for any object $y\in \mathcal {E}_y$, the square $(I)+(II)=(III)+(IV)$ is a homotopy pullback, we conclude that the square (23) is a homotopy pullback if and only if the square (III) is as well, which holds if and only if the 2-functor $\bar{h}_*:\Gamma _{\!c}\!\downarrow \!y\rightarrow \Gamma _{\!c'}\!\downarrow \!h_*y$ is a weak equivalence. $\square$

Similarly, if $\mathcal {D},\,\mathcal {E}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$ are 2-functors and $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ is a 2-transformation, for any objects $c\in C$ and $y\in \mathcal {E}_{c}$, there is a commutative square

(27)

defined as the composite of the squares

and we have the theorem below.

Theorem 4.2

(Theorem $\mathrm {B}_r$ for 2-transformations) Let $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ be a 2-transformation, where $\mathcal {D},\,\mathcal {E}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$ are 2-functors. The following properties are equivalent:

• (a) For any object c in C and any object y in $\mathcal {E}_c$, the square (27) is a homotopy pullback.

• (b) The 2-functor $\int _C\Gamma :\int _C\mathcal {D}\rightarrow \int _C\mathcal {E}$ has the property $\mathrm {B}_r$.

• (c) The two conditions below hold.

  • $\mathrm {B1}_r$: For each object c of C, the 2-functor $\Gamma _c:\mathcal {D}_c\rightarrow \mathcal {E}_c$ has the property $\mathrm {B}_r$.

  • $\mathrm {B2}_r$: For each 1-cell $h:c\rightarrow c'$ in C and any object $y'\in \mathcal {E}_{c'}$, the induced 2-functor

    

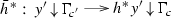
    is a weak equivalence.

• (d) The two conditions below hold.

  • $\mathrm {B1}_r$: For each object c of C, the 2-functor $\Gamma _c:\mathcal {D}_c\rightarrow \mathcal {E}_c$ has the property $\mathrm {B}_r$.

  • $\mathrm {B2}'_r$: For each 1-cell $h:c\rightarrow c'$ in C, the square

    

    is a homotopy pullback.

Proof

This is parallel to the proof of Theorem 4.1 given above, and we leave it to the reader. We simply note that, in this case, the weak equivalence

(28)

for each objects $c\in C$ and $y\in \mathcal {E}_c$, is defined as below.

On objects $((x,a),(p,v))\in (c,y)\! \downarrow \!\int _C\!\Gamma$, where a is an object of C, x an object of $\mathcal {D}_a$, $p:c\rightarrow a$ is a 1-cell in C and $v:y\rightarrow p^*\Gamma _{\!a}x=\Gamma _{\!c}p^*x$ is a 1-cell in $\mathcal {E}_c$,

$$\begin{aligned} R((a,x),(p,v))=(p^*x,v). \end{aligned}$$

On 1-cells $((f,u),(\alpha ,\psi )):((a,x),(p,v))\rightarrow ((a',x'),(p',v'))$ where $f:a\rightarrow a'$ is in $\mathcal {C}$, $u:x\rightarrow f^*x'$ in $\mathcal {D}_a$, $\alpha : f\circ p\Rightarrow \circ p'$ in C, and $\psi : \alpha ^*\Gamma _{\!a'}x'\circ p^*\Gamma _{\!a}u\circ v \Rightarrow v'$ in $\mathcal {E}_c$,

$$\begin{aligned} R((f,u),(\alpha ,\psi ))=(\alpha ^*x'\circ p^*u,\psi ):(p^*x,v)\rightarrow (p'^*x',v'), \end{aligned}$$

and, for a 2-cell $(\beta ,\phi ):((f,u),(\alpha ,\psi ))\Rightarrow ((f',u'),(\alpha ',\psi '))$, where $\beta :f\Rightarrow f'$ is in C and $\phi :\beta ^*x'\circ u\Rightarrow u'$ in $\mathcal {D}_a$,

$$\begin{aligned} R(\beta ,\phi )= 1_{\alpha '^*x'}\circ p^*\phi :(\alpha ^*x'\circ p^*u,\psi )\Rightarrow ( \alpha '^*x'\circ p^*u',\psi '). \end{aligned}$$

$\square$

Observe that, in the particular case where $C=\star$ the terminal 2-category, Theorems 4.1 and 4.2 state exactly the same as Theorem 2.3.

Furthermore, in the specific case where $\mathcal {E}=\star$ is the constant terminal 2-category, for any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ or $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the projection 2-functors $\pi$ are actually isomorphisms $\Gamma _{\!c}\!\downarrow \!\star \cong \mathcal {D}_{\!c}\cong \star \!\downarrow \!\Gamma _{\!c}$, and Theorems 4.1 and 4.2 give as a corollary the following 2-categorical version of the relevant Quillen’s detection principle for homotopy pullback diagrams  [29, Lemma in p. 14] (see  [11, Theorem 4.3] for a more general bicategorical result). Let us also stress that the weak equivalences (24) and (28), in this case where $\mathcal {E}=\star$, establish weak equivalences

between the homotopy-fibre 2-categories of the projection 2-functor $\pi :\int _C\mathcal {D}\rightarrow C$ over the objects of C and the 2-categories attached by the 2-diagram to these objects.

Corollary 4.1

(Detecting homotopy pullbacks) Let C be a 2-category. For any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (resp. $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$), the following statements are equivalent:

• (a) For any object c in C the square

  

  (29)

  is a homotopy pullback.

• (b) The projection 2-functor $\pi :\int _C\mathcal {D}\rightarrow C$ has the property $\mathrm {B}_l$ (resp. $\mathrm {B}_r$).

• (c) For each 1-cell $h:c\rightarrow c'$ of C, the 2-functor $h_*:\mathcal {D}_{\!c}\rightarrow \mathcal {D}_{\!c'}$ (resp. $h^*:\mathcal {D}_{\!c'}\rightarrow \mathcal {D}_{\!c}$) is a weak equivalence.

The following consequence of Theorems 4.1 and 4.2 is closely related to Theorems 3.2 and 2.4.

Corollary 4.2

(Theorem A for 2-diagrams) Let $\Gamma :\mathcal {D}\Rightarrow \mathcal {E}$ be a 2-transformation, where $\mathcal {D},\,\mathcal {E}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (resp. $\mathcal {D},\,\mathcal {E}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$) are 2-functors. The following statements are equivalent:

• (a) The 2-functor $\int _C\Gamma :\int _C\mathcal {D}\rightarrow \int _C\mathcal {E}$ is homotopy left (resp. right) cofinal.

• (b) For any object $c\in C$, the 2-functor $\Gamma _{\!c}:\mathcal {D}_c\rightarrow \mathcal {E}_c$ is homotopy left (resp. right) cofinal.

5 Changing the indexing 2-category

If $F:A\rightarrow C$ is a 2-functor between 2-categories, then any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, or $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$, gives rise to a pullback of 2-categories

(30)

where $\bar{F}$ is given by

(31)

Our first result here completes Corollary 4.1:

Theorem 5.1

Let C be a 2-category and $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (resp. $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$) a 2-functor. The following statements are equivalent:

• (a) For any 2-functor $F:A\rightarrow C$, the square (30) is a homotopy pullback.

• (b) For any 1-cell $h:c\rightarrow c'$ in C, the 2-functor $h_*:\mathcal {D}_{\!c}\rightarrow \mathcal {D}_{\!c'}$ (resp. $h^*:\mathcal {D}_{\!c'}\rightarrow \mathcal {D}_{\!c}$) is a weak equivalence.

Proof

Suppose (a) holds. Let $c:\mathrm { pt}\rightarrow C$ be the 2-functor given by any object $c\in C$. As we have quite an obvious isomorphism $\int _{\star }c^*\mathcal {D}\cong \mathcal {D}_{\!c}$, the square

(32)

is, by hypothesis, a homotopy pullback. Hence, the result follows from Corollary 4.1.

Conversely, assume (b) holds. Again by Corollary 4.1, for any object $c\in C$, the square (32) above is a homotopy pullback. Since, for any given 2-functor $F:A\rightarrow C$, the 2-functor $F^*\!\mathcal {D}:A\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (resp. $F^*\!\mathcal {D}:A^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$) trivially is under the same hypothesis (b) as $\mathcal {D}$, it follows that, for any object $a\in A$, both the left side and the composite square in the diagram

are homotopy pullbacks. Then, from the homotopy fibre characterization of homotopy pullbacks, it follows that the right side square above is a homotopy pullback, as required. $\square$

Next, we state the complementary counterpart to the theorem above. If $F:A\rightarrow C$ and $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$ are 2-functors, for any objects $c\in C$ and $z\in \mathcal {D}_{\!c}$, let

be the 2-functor defined on cells by

(33)

Theorem 5.2

For a 2-functor $F:A\rightarrow C$, the following statements are equivalent:

• (a) $F:A\rightarrow C$ has the property $\mathrm {B}_l$.

• (b) For any 2-functor $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the 2-functor $\bar{F}:\int _AF^*\mathcal {D}\rightarrow \int _C\mathcal {D}$ has the property $\mathrm {B}_l$.

• (c) For any 2-functor $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$, and any objects $c\in C$ and $z\in \mathcal {D}_{\!c}$, the commutative square

  

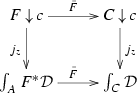  (34)

  is a homotopy pullback.

• (d) For any 2-functor $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the square (30)

  

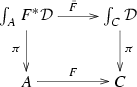
  is a homotopy pullback.

Proof

For any objects $c\in C$ and $z\in \mathcal {D}_{\!c}$, let

(35)

be the induced 2-functor on homotopy-fibre 2-categories making the diagram below commutative:

Explicitly, this $\bar{\pi }$ acts on objects ((a, x), (p, v)), where a is an object of A, x an object of $\mathcal {D}_{F\!a}$, $p:Fa\rightarrow c$ is a 1-cell in C and $v:x\rightarrow p^*z$ is a 1-cell in $\mathcal {D}_{Fa}$, by

$$\begin{aligned} \bar{\pi }((a,x),(p,v))=(a,p). \end{aligned}$$

On 1-cells

$$\begin{aligned} ((f,u),(\phi ,\beta )):((a,x),(p,v))\rightarrow ((a',x'),(p',v')), \end{aligned}$$

(36)

where $f:a\rightarrow a'$ is a 1-cell of A, $u:x\rightarrow (Ff)^*x'$ of $\mathcal {D}_{F\!a}$, $\phi :p\Rightarrow p'\circ Ff$ a 2-cell of C, and $\beta :\phi ^*z\circ v\Rightarrow (Ff)^*v'\circ u$ a 2-cell of $\mathcal {D}_{F\!a}$,

$$\begin{aligned} \bar{\pi }((f,u),(\phi ,\beta ))=(f,\phi ):(a,p)\rightarrow (a',p'), \end{aligned}$$

and, on a 2-cell $(\alpha ,\psi ):((f,u),(\phi ,\beta ))\Rightarrow ((f',u'),(\phi ',\beta '))$, where $\alpha :f\Rightarrow f'$ is a 2-cell of A and $\psi :(F\alpha )^*x'\circ u\Rightarrow u'$ a 2-cell in $\mathcal {D}_{Fa}$, satisfying the corresponding conditions,

$$\begin{aligned} \bar{\pi }(\alpha ,\psi )=\alpha :(f,\phi )\Rightarrow (f',\phi '). \end{aligned}$$

The 2-functor $\bar{\pi }$ is actually a retraction, with a section given by the 2-functor

which acts on objects by

$$\begin{aligned} i_z(a,p)=((a,p^*z),(p,1_{p^*z})), \end{aligned}$$

on a 1-cell $(f,\phi ):(a,p)\rightarrow (a',p')$ by

$$\begin{aligned} i_z(f,\phi )=((f,\phi ^*z),(\phi ,1_{\phi ^*z})):((a,p^*z),(p,1_{p^*z})) \rightarrow ((a',p'^*z),(p',1_{p'^*z})), \end{aligned}$$

and on a 2-cell $\alpha :(f,\phi )\Rightarrow (f',\phi ')$ by

$$\begin{aligned} i_z(\alpha )=(\alpha ,1_{\phi ^*z}):((f,\phi ^*z),(\phi ,1_{\phi ^*z}))\Longrightarrow ((f',\phi '^*z),(\phi ',1_{\phi '^*z})). \end{aligned}$$

It is clear that $\bar{\pi }\,i_z=1$. Furthermore, there is an oplax transformation $1\Rightarrow i_z\,\bar{\pi }$ given, on any object ((a, x), (p, v)) of $\bar{F}\!\downarrow \!(c,z)$, by the 1-cell

$$\begin{aligned} ((1_a,v),(1_p,1_v)): ((a,x),(p,v))\rightarrow ((a,p_*z),(p,1_{p^*z})), \end{aligned}$$

and whose naturality component at any 1-cell as in (36) is

Hence, for the maps induced by $\bar{\pi }$ and $i_z$ on classifying spaces, $|\!|\bar{\pi }|\!|\,|\!|i_z|\!|=1$ and, by Fact 2.2, $1\simeq |\!|i_z|\!|\,|\!|\bar{\pi }|\!|$. Therefore, both 2-functors $\bar{\pi }$ and $i_z$ are weak equivalences.

Let us now observe that the square (34) is the composite of the squares

where both vertical 2-functors $i_z$ are weak equivalences. It follows that the square (34) is a homotopy pullback if and only if the square (I) above is as well. As, by Theorem 2.3, the squares (I) are homotopy pullbacks, for all objects (c, z) of $\int _C\mathcal {D}$, if and only if the 2-functor $\bar{F}:\int _AF^*\mathcal {D}\rightarrow \int _C\mathcal {D}$ has the property $\mathrm {B}_l$, the equivalence $(b)\Leftrightarrow (c)$ is proven.

The equivalence $(a)\Leftrightarrow (b)$ follows from the fact that, for any 1-cell $(h,w):(c,z)\rightarrow (c',z')$ in $\int _C\mathcal {D}$, the square of 2-functors

commutes, where, recall, both vertical 2-functors $\bar{\pi }$ are weak equivalences. So, the 2-functors $\overline{(h,w)}_*$ at the top are weak equivalences if and only if the 2-functors $\bar{h}_*$ at the bottom are as well. This directly means that $(a)\Rightarrow (b)$, and the converse follows from taking any $\mathcal {D}$ such that $\mathcal {D}_c\ne \emptyset$ for all $c\in C$.

Next, we prove that $(c)\Rightarrow (d)$: For any object (c, z) of $\int _C\mathcal {D}$, we have the squares

whose composite is the left square in (10), and where $j_z(1_c)=(c,z)$. By hypothesis, the left square is a homotopy pullback. Furthermore, as F has the property $\mathrm {B}_l$, owing to the already proven implication $(c)\Rightarrow (a)$, Theorem 2.3 implies that the composite square is also a homotopy pullback. Therefore, by the homotopy fibre characterization, the right square above is a homotopy pullback as well.

Finally, $(d)\Rightarrow (a)$ is easy: For any object $c\in C$ take $\mathcal {D}=C(-,c):C^{\mathrm {op}}\rightarrow {\underline{\mathbf{Cat}}}\subseteq$ ${\underline{\mathbf{2Cat}}}$. Then, by hypothesis, the square

is a homotopy pullback, whence the result follows from Theorem 2.3. $\square$

Likewise, if $F:A\rightarrow C$ and $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ are 2-functors, for any objects $c\in C$ and $z\in \mathcal {D}_{\!c}$, we have the 2-functor

given by

and the result below holds.

Theorem 5.3

For a 2-functor $F:A\rightarrow C$, the following statements are equivalent:

• (a) $F:A\rightarrow C$ has the property $\mathrm {B}_r$.

• (b) For any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the 2-functor $\bar{F}:\int _AF^*\mathcal {D}\rightarrow \int _C\mathcal {D}$ has the property $\mathrm {B}_r$.

• (c) For any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, and any objects $c\in C$ and $z\in \mathcal {D}_{\!c}$, the commutative square

  

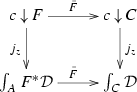
  is a homotopy pullback.

• (d) For any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the square (30)

  

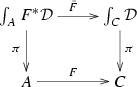
  is a homotopy pullback.

A main consequence is the corollary below.

Corollary 5.1

(Homotopy Cofinality Theorem) Let $F:A\rightarrow C$ be a 2-functor between 2-categories. The statements below are equivalent.

• (a) $F:A\rightarrow C$ is homotopy left (resp. right) cofinal.

• (b) For any 2-functor $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (resp. $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$) the induced 2-functor $\bar{F}:\int _AF^*\mathcal {D}\rightarrow \int _C\mathcal {D}$ is homotopy left (resp. right) cofinal.

• (c) For any 2-functor $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$ (resp. $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$) the induced 2-functor $\bar{F}:\int _AF^*\mathcal {D}\rightarrow \int _C\mathcal {D}$ is a weak equivalence.

Proof

The equivalence $(a)\Leftrightarrow (b)$ follows from Theorems 5.2 and 5.3. The implication $(b)\Rightarrow (c)$ follows from Theorem 2.4. To prove the remaining $(c)\Rightarrow (a)$, take, for any object c of $\mathcal {C}$, the 2-functor $\mathcal {D}=C(-,c):C^{\mathrm {op}}\rightarrow {\underline{\mathbf{Cat}}}\subseteq {\underline{\mathbf{2Cat}}}$. Then, by hypothesis, the 2-functor

is a weak equivalence. Therefore, $F\!\downarrow \!c$ is weakly contractible as $C\!\downarrow \!c$ is, by Lemma 2.1. $\square$

Next, we show conditions on a 2-category C in order for the square (30) to always be a homotopy pullback.

Corollary 5.2

Let C be a 2-category. Then, the following properties are equivalent:

• (i) For any 1-cell $h:c\rightarrow c'$ and any object x of C, the functor $h_*:C(x,c)\rightarrow C(x,c')$ is a weak equivalence.

• (i’) For any 1-cell $h:c\rightarrow c'$ and any object x of C, the functor $h^*:C(c',x)\rightarrow C(c,x)$ is a weak equivalence.

• (ii) For any two objects $c,c'\in C$, the canonical square

  

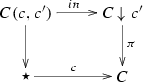
  is a homotopy pullback.⁸

• (ii’) For any two objects $c,c'\in C$, the canonical square

  

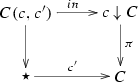
  is a homotopy pullback.

• (iii) For any 2-functor $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the 2-functor ${h}_*:\mathcal {D}_{\!c}\rightarrow \mathcal {D}_{\!c'}$ induced for any 1-cell $h:c\rightarrow c'$ of C is a weak equivalence.

• (iii’) For any 2-functor $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the 2-functor ${h}^*:\mathcal {D}_{\!c'}\rightarrow \mathcal {D}_{\!c}$ induced for any 1-cell $h:c\rightarrow c'$ of C is a weak equivalence.

• (iv) For any 2-functors $F:A\rightarrow C$ and $\mathcal {D}:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the square

  

  is a homotopy pullback.

• (iv’) For any 2-functors $F:A\rightarrow C$ and $\mathcal {D}:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$, the square

  

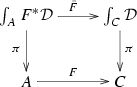
  is a homotopy pullback.

• (v) Any 2-functor $F:A\rightarrow C$ has the property $\mathrm {B}_r$.

• (v’) Any 2-functor $F:A\rightarrow C$ has the property $\mathrm {B}_l$.

Proof

$(\mathrm{i})\Leftrightarrow (\mathrm{ii})$:⁹ Let $c:\star \rightarrow C$ be the 2-functor given for any object $c\in C$. Then, for any object $x\in C$, there is quite an obvious natural isomorphism

between the homotopy-fibre 2-category (actually a category) of $c:\star \rightarrow C$ over x and the hom-category C(c, x). Then, any 1-cell $h:x\rightarrow y$ in C induces a weak equivalence $h_*:c\!\downarrow \!x\rightarrow c\!\downarrow \!y$ if and only if the induced $h_*:C(c,x)\rightarrow C(c,y)$ is a weak equivalence. It follows that the 2-functor $c:\star \rightarrow C$ has the property $\mathrm {B}_l$ if and only if the hypothesis in $(\mathrm{i})$ holds. On the other hand, by Theorem 2.3, the 2-functor $c:\star \rightarrow C$ has the property $\mathrm {B}_l$ if and only if, for any object $c'\in C$, the square

is a homotopy pullback, that is, if and only if $(\mathrm{ii})$ holds.

$(\mathrm{iii})\Rightarrow (\mathrm{i})$: For any object $x\in C$, the result follows by applying the hypothesis in $(\mathrm{iii})$ to the 2-functor $\mathcal {D}=C(x,-):C\rightarrow {\underline{\mathbf{Cat}}}$.

$(\mathrm{i})\Rightarrow (\mathrm{v})$  By Theorem 5.1, for any 2-functor $F:A\rightarrow C$ and any object $c\in C$, the square

is a homotopy pullback. Then, F has the property $\mathrm {B}_r$ by Theorem 2.3.

$(\mathrm{v})\Rightarrow (\mathrm{iv})$  This follows from Theorem 5.3.

$(\mathrm{iv})\Rightarrow (\mathrm{iii})$  This follows from Theorem 5.1.

Thus, we have $(\mathrm{i})\Leftrightarrow (\mathrm{ii})\Leftrightarrow (\mathrm{iii})\Leftrightarrow (\mathrm{iv})\Leftrightarrow (\mathrm{v})$ and, similarly, we also have the equivalences $(\mathrm{i}')\Leftrightarrow (\mathrm{ii}')\Leftrightarrow (\mathrm{iii}')\Leftrightarrow (\mathrm{iv}')\Leftrightarrow (\mathrm{v}')$.

Furthermore, for any given 2-functor $F:A\rightarrow C$, the application of the hypothesis in $(\mathrm{iii})$ to the homotopy-fibre 2-functor $F\!\downarrow \!-:C\rightarrow$ ${\underline{\mathbf{2Cat}}}$ just says that F has the property $\mathrm {B}_l$. Hence, $(\mathrm{iii})\Rightarrow (\mathrm{v}')$. Likewise, for any 2-functor $F:A\rightarrow C$, the hypothesis on $-\!\downarrow \!F:C^{\mathrm {op}}\rightarrow$ ${\underline{\mathbf{2Cat}}}$ implies that F has the property $\mathrm {B}_r$, whence $(\mathrm{iii}')\Rightarrow (\mathrm{v})$, and the proof is complete. $\square$

Remark 1

If $\phi :A\rightarrow C$ and $\phi ':A'\rightarrow C$ are continuous maps between spaces, its homotopy-fibre product $A\times ^{_\mathrm {h}}_CA'$ is the subspace of the product $A\times B^I\!\times A'$, where $I=[0,1]$ and $C^{I}$ is taken with the compact-open topology, whose points are triples $(a,\gamma ,a')$ with $a\in A$, $a'\in A'$, and $\gamma : \phi a\rightarrow \phi 'a'$ a path in C joining $\phi a$ and $\phi ' a'$, that is, $\gamma :I\rightarrow C$ is a path with $\gamma 0=\phi a$ and $\gamma 1=\phi ' a'$.

There is a subtle 2-categorical emulation of the homotopy-fibre product of spaces: Any pair of 2-functors $F:A\rightarrow C$ and $F':A'\rightarrow C$, where A, C, and $A'$ are 2-categories, has associated a comma 2-category $F\!\downarrow \!F'$, whose 0-cells are triples $(a,f,a')$ with $f:Fa\rightarrow F'a'$ a 1-cell in C, whose 1-cells $(u,\beta ,u'):(a_0,f_0,a'_0)\Rightarrow (a_1,f_1,a'_1)$ are triples consisting of 1-cells $u:a_0\rightarrow a_1$ in A and $u':a'_0\rightarrow a'_1$ in $A'$, together with a 2-cell $\beta : F'u'\circ f_0\Rightarrow f_1\circ Fu$ in C, and 2-cells $(\alpha ,\alpha '):(u,\beta ,u')\Rightarrow (v,\gamma ,v')$ pairs given by 2-cells $\alpha :u\Rightarrow v$ in A and $\alpha ':u'\Rightarrow v'$ in $A'$ such that $(1_{f_1}\circ F\alpha )\cdot \beta =\gamma \cdot (F'\alpha '\circ 1_{f_0})$. This 2-category $F\!\downarrow \!F'$ comes with a canonical map from its classifying space to the homotopy-fibre product space of the induced maps $|\!|F|\!|:|\!|A|\!|\rightarrow |\!|C|\!|$ and $|\!|F'|\!|:|\!|A'|\!|\rightarrow |\!|C |\!|$,

$$\begin{aligned} |\!|F\!\downarrow \!F'|\!|\rightarrow |\!|A|\!|\times ^{_\mathrm h}_{|\!|C|\!|}|\!|A|\!|, \end{aligned}$$

which, by  [15, Theorem 3.8], is a homotopy equivalence whenever the equivalent conditions of Corollary 5.2 on the 2-category C hold.

To finish, let us remark that the class of 2-categories satisfying the conditions in Corollary 5.2 above includes those 2-categories C where, for each 1-cell $f:c\rightarrow c'$, there exists a 1-cell $f':c'\rightarrow c$ such that $[f'\circ f]=[1_c]\in \pi _0C(c,c)$ and $[f\circ f']=[1_{c'}]\in \pi _0C(c',c')$. In particular, the result applies to 2-groupoids, whose 1-cells are all invertible, which, recall, are equivalent to crossed modules over groupoids by Brown and Higgins  [8].