A short-time drift propagator approach to the Fokker–Planck equation

Abstract

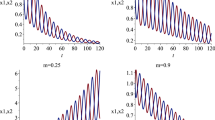
The Fokker–Planck equation is a partial differential equation that describes the evolution of a probability distribution over time. It is used to model a wide range of physical and biological phenomena, such as diffusion, chemical reactions, and population dynamics. Solving the Fokker–Planck equation is a difficult task, as it involves solving a system of coupled nonlinear partial differential equations. In general, analytical solutions are not available and numerical methods must be used. In this research, we propose a novel approach to the solution of the Fokker–Planck equation in a short time interval. The numerical solution to the equation can be obtained iteratively using a new technique based on the short-time drift propagator. This new approach is different from the traditional methods, as the state-dependent drift function has been removed from the multivariate Gaussian integral component and is instead presented as a state-shifted element. We evaluated our technique employing a fundamental Wiener process with constant drift components in both one- and two-dimensional space. The results of the numerical calculation were found to be consistent with the exact solution. The proposed approach offers a promising new direction for research in this area.