Abstract
When the available pressure at the nodes becomes less than the minimum pressure, the network is said to be in pressure-deficient condition, and under such a condition the demand at the nodes cannot be satisfied. In the pressure-deficient condition, as such, the demand-driven solver does not work and the solution requires that the node flow equation should be embedded either internally or externally in the demand-driven solver. In the last decade, researchers have focused considerable attention on the solution of pressure-deficient conditions using a demand-driven solver. The objective of the study is to compare the methods for the solution of pressure-deficient networks using either artificial reservoirs or emitter features of the demand-driven solver. Both the approaches are applied to three different benchmark water distribution networks, data for which are adopted from literature. In any real-world water distribution network, the field observed data for validation of results of simulation are normally not available because of different demand conditions in real time, condition of the existing pipe, the variation of hydraulic pressure, etc. Thus, this comparative study would be useful for water distribution network practitioners and field engineers to validate the results obtained by one method. It is found that both methods have some common structures that can be utilized in the validation of the results. The comparative study further shows that a simple modification in the structure of one method of solution yields the solution by another method. The results show that the pressure-deficient network can be analyzed successfully using either the artificial reservoir or emitter feature of the graphical user interface of EPANET 2.0. Under the condition of a very small difference between the required and minimum head values at a node, it is found that both the approaches provide a similar result for the water distribution network considered. However, the approach based on the emitter is found to be more flexible in handling the nodal head–flow relation, provided appropriate emitter coefficient and emitter exponent are used. Moreover, it has been observed that in a network, the pressure-deficient nodes are not fixed and change during the simulation period depending on the demand pattern, reservoir level, etc., and hence cannot be identified at the beginning of the simulation.














Similar content being viewed by others
References
R. Gupta, P.R. Bhave, Comparison of methods for predicting pressure-deficient-network performance. J. Water Resour. Plann. Manage. 122(3), 214–217 (1996)
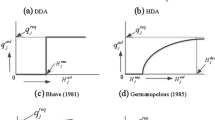
P.R. Bhave, Node flow analysis of water distribution systems. J. Transp. Eng. 107(4), 457–467 (1981)
S.S. Ozger, L.W. Mays, A Semi-Pressure Driven Approach to Reliability Assessment of Water Distribution Network (Proc. IAHR Congress, Aristoteleio Panepistimio Thessalonikis, Thessaloniki, Greece, 2003), pp. 345–352
Z.Y. Wu, R.H. Wang, T.M. Walsiki, S.Y. Yang, D. Bowdler, C.C. Baggett, Extended global gradient algorithm for pressure-dependent water distribution analysis. J. Water Resour. Plann. and Manage. 135(1), 13–22 (2009)
T. Tanyimboh, A.B. Templeman, Seamless pressure-deficient water distribution system model. Proc. ICE. Water Manage. 163(8), 389–396 (2010)
C. Siew, T.T. Tanyimboh, Pressure-dependent EPANET extension. Water Resour. Manag. 26(6), 1477–1498 (2012)
Ho Min Lee, Do Guen Yoo, Kim Joong Hoon, Doosun Kang, Hydraulic simulation techniques for water distribution networks to treat pressure-deficient conditions. J. Water Resour. Plann. Manage. 142(4), 06015003 (2016)
W.K. Ang, P.W. Jowitt, Solution for water distribution systems under pressure-deficient conditions. J. Water Resour. Plann. Manage. 132(3), 175–182 (2006)
C.R. Suribabu, T.R. Neelakantan, Balancing reservoir based approach for a solution to pressure-deficient water distribution networks. Int. J. Civ. Struct. Eng. 2(2), 639–647 (2011)
K.S. Jinesh Babu, S. Mohan, Extended period simulation for pressure-deficient water distribution network. J. Comput. Civ. Eng. 26(4), 498–505 (2012)
P. Sivakumar, R.K. Prasad, Simulation of water distribution network under pressure-deficient condition. Water Resour. Mange. 28(10), 3271–3290 (2014)
D. Paez, C.R. Suribabu, Y. Fillon, Method for extended period simulation of water distribution network with pressure-driven demands. Water Resour. Mange. 32(8), 2837–2846 (2018)
L. A. Rossman, EPANET 2.0 user’s manual. Risk Reduction Engineering Laboratory, US Environmental Protection Agency, Cincinnati (2000)
E. Todini, S. Pilati, A Gradient Method for the Analysis of Pipe Networks Proc Computer Applications for Water Supply and Distribution (U. K, Leicester Polytechnic, 1978), pp. 8–10
L. A. Rossman, H. Woo, M. Tryby, F. Shang, R. Junke, and T. Haxton. EPANET 2.2 user’s manual. U.S. Environmental Protection Agency Cincinnati, (2020)
N.B. Gorev, V.N. Gorev, I.F. Kodzhespirova, I.A. Shediovsky, P. Sivakumar, Technique for pressure-driven analysis of water distribution networks with flow and pressure-regulating valves. J. Water Resour. Plann. Manage. 147(5), 06021005 (2021)
Z.Y. Wu, Discussion of ‘Solution for water distribution systems under pressure-deficient conditions’ by W. K. Ang and P. W. Jowitt. J Water Resour Plann Manage 133(6), 567–568 (2007)
N.B. Gorev, I.F. Kodzhespirova, Non-iterative implementation of pressure-dependent demands using the hydraulic analysis engine of EPANET 2. Water Resour. Mange. 27(10), 3623–3630 (2013)
J.M. Wagner, U. Shamir, D.H. Marks, Water distribution reliability: Simulation methods. J. Water Resour. Plann. Manage. 114(3), 276–294 (1988)
P. Sivakumar, R.K. Prasad, Extended period simulation of pressure-deficient networks using a pressure reducing valves. Water Resour. Manag. 29(5), 1719–1730 (2015)
L.A. Rossman, Discussion of ‘Solution for water distribution systems under pressure-deficient conditions’ by W. H. Ang and P. W. Jowitt. J Water Resour Plann Manage 133(6), 566–567 (2007)
M.A.H. Abdy Sayyed, R. Gupta, T.T. Tanyimboh, Non-iterative application of EPANET 20 for pressure-dependent modeling of water distribution systems. Water Resour. Mange 29(9), 3227–3242 (2015)
C.R. Suribabu, Emitter-based approach for estimation of nodal outflow to pressure-deficient water distribution networks under pressure management. Sci. Iran. Trans. 22, 1765–1778 (2015)
C.R. Suribabu, T.R. Neelakantan, P. Sivakumar, Diego Paez, Analysis of water distribution network under pressure-deficient conditions through emitter setting. Drink. Water Eng. Sci. 12, 1–13 (2019)
H.A. Mahmoud, D. Savic, Z. Kapelan, New pressure-driven approach for modeling water distribution networks. J. Water Resour. Plann. Manage. 143(8), 04017031 (2017)
T.R. Neelakantan, K. Rohini, Simplified pressure-driven analysis of water distribution network and resilience estimation. J. Water Resour. Plann. Manage. 147(3), 06021002 (2021)
G. Germanopoulos, A technical note on the inclusion of pressure-dependent and leakage term in water supply network models. Civ. Eng. Syst. 2(3), 171–179 (1985)
J. Chandapillai, K.P. Sudheer, S. Saseendran, Design of water distribution network for equitable supply. Water Resour. Manage. 26(2), 391–406 (2012)
R. Gupta, M.A.H. Abdy Sayyed, T.T. Tanyimboh, Discussion of ‘New pressure-driven approach for modeling water distribution networks’ by H. A. Mahmoud, D. Savic, and Z. Kapelan. J. Water Resour. Plann. Manage. 144(6), 07018006 (2018)
Funding
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Prasad, R.K., Kamda, G. Comparison of Methods for the Solution of Pressure-Deficient Networks using Artificial Elements. J. Inst. Eng. India Ser. A 102, 959–972 (2021). https://doi.org/10.1007/s40030-021-00560-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40030-021-00560-x