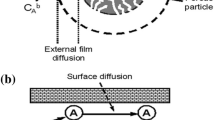
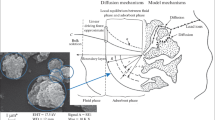
Abstract
Cadmium(II) is a toxic hazardous cation, whose presence in the environment causes great concern because of its bioaccumulation in organisms and bioamplification along food chain. Hence, the removal of cadmium compounds from industrial waters and wastewaters is particularly essential, which requires intensive experimental and modelling studies to deal with the problem. In this work, the ion exchange of Cd2+ ions from aqueous solution using microporous titanosilicates (ETS-4 and ETS-10) has been modelled using adapted Maxwell–Stefan equations for the ions transport inside the sorbent particles. The fundamentals of the Maxwell–Stefan equations along with correlations for the convective mass transfer coefficients have been used with advantage to reduce the number of model parameters. In the whole, the model was able to represent successfully the kinetic behaviour of 11 independent and very distinct curves of both studied systems (Cd2+/Na+/ETS-4 and Cd2+/Na+/ETS-10). The predictive capability of the model has been also shown, since several uptake curves were accurately predicted with parameters fitted previously to different sets of experimental data.




Similar content being viewed by others
References
Armenante PM, Kirwan DJ (1989) Mass-transfer to microparticles in agitated systems. Chem Eng Sci 44(12):2781–2796
Barreira LD, Lito PF, Antunes BM, Otero M, Lin Z, Rocha J, Pereira E, Duarte AC, Silva CM (2009) Effect of pH on cadmium(II) removal from aqueous solution using titanosilicate ETS-4. Chem Eng J 155(3):728–735
Camarinha ED, Lito PF, Antunes BM, Otero M, Lin Z, Rocha J, Pereira E, Duarte AC, Silva CM (2009) Cadmium(II) removal from aqueous solution using microporous titanosilicate ETS-10. Chem Eng J 155(1–2):108–114
Chanda M, Rempel GL (1995) Sorption of sulfide on a macroporous, quaternized poly(4-vinyl pyridine) in alkaline medium. React Polym 24(3):203–212
Choi JH, Kim SD, Kwon YJ, Kim WJ (2006) Adsorption behaviors of ETS-10 and its variant, ETAS-10 on the removal of heavy metals, Cu2+, Co2+, Mn2+ and Zn2+ from a waste water. Microporous Mesoporous Mater 96(1–3):157–167
Cincotti A, Mameli A, Locci AM, Orru R, Cao G (2006) Heavy metals uptake by Sardinian natural zeolites: experiment and modeling. Ind Eng Chem Res 45(3):1074–1084
Clark RB, Frid C, Attrill M (2001) Marine pollution. Oxford press, Oxford
Dabrowski A, Hubicki Z, Podkoscielny P, Robens E (2004) Selective removal of the heavy metal ions from waters and industrial wastewaters by ion-exchange method. Chemosphere 56(2):91–106
Dolgonosov AM, Khamizov RK, Krachak AN, Prudkovsky AG (1995) Macroscopic model for multispecies ion-exchange kinetics. React Funct Polym 28(1):13–20
Ferreira TR, Lopes CB, Lito PF, Otero M, Lin Z, Rocha J, Pereira E, Silva CM, Duarte A (2009) Cadmium(II) removal from aqueous solution using microporous titanosilicate ETS-4. Chem Eng J 147(2–3):173–179
Graham EE, Dranoff JS (1982a) Application of the Stefan–Maxwell equations to diffusion in ion-exchangers. 1. Theory. Ind Eng Chem Fundam 21(4):360–365
Graham EE, Dranoff JS (1982b) Application of the Stefan–Maxwell equations to diffusion in ion-exchangers. 2. Experimental results. Ind Eng Chem Fundam 21(4):365–369
Helfferich F (1995) Ion exchange. Dover, New York
Hogendoorn JA, AJVd Veen, JHGVd Stegen, Kuipers JAM, Versteeg GF (2001) Application of the Maxwell–Stefan theory to the membrane electrolysis process: model development and simulation. Comput Chem Eng 25:1251–1265
Jackson R (1977) Transport in porous catalysts. Elsevier, Amsterdam
Kraaijeveld G, Sumberova V, Kuindersma S, Wesselingh H (1995) Modeling electrodialysis using the Maxwell–Stefan description. Chem Eng J Biochem Eng J 57(2):163–176
Krishna R, Wesselingh JA (1997) Review article number 50—the Maxwell–Stefan approach to mass transfer. Chem Eng Sci 52(6):861–911
Kulov NN, Nikolaishvili EK, Barabash VM, Braginski LN, Malyusov VA, Zhavoronkov NM (1983) Dissolution of solid particles suspended in agitated vessels. Chem Eng Commun 21(4–6):259–271
Lito PF, Silva CM (2008) Comparison between Maxwell–Stefan and Nernst–Planck equations to describe ion exchange in microporous materials. Defect Diffus Forum 273–276:776–781
Lito PF, Cardoso SP, Loureiro JM, Silva CM (2012). Ion-exchange equlibria and kinetics. In: Inamuddin S, Luqman M (eds) Ion-exchange technology: theory, materials and applications, chap 3, pp 51–120. Springer, Berlin
Lopes CB, Otero M, Coinbra J, Pereira E, Rocha J, Lin Z, Duarte A (2007) Removal of low concentration Hg2+ from natural waters by microporous and layered titanosilicates. Micropor Mesopor Mat 103(1–3):325–332
Lopes CB, Otero M, Lin Z, Silva CM, Rocha J, Pereira E, Duarte AC (2009) Removal of Hg2+ ions from aqueous solution by ETS-4 microporous titanosilicate - Kinetic and equilibrium studies. Chem Eng J 151(1–3):247–254
Lito PF, Aniceto JPS, Silva CM (2013) Modelling ion exchange kinetics in zeolyte-type materials using Maxwell–Stefan approach. Desalination Water Treat. doi:10.1080/19443994.2013.815682
Lv L, Wang K, Zhao XS (2007) Effect of operating conditions on the removal of Pb2+ by microporous titanosilicate ETS-10 in a fixed-bed column. J Colloid Interface Sci 305(2):218–225
Miller SA, Amber CM, Bennet RC, Dahlstrom DA, Darji JD, Emmet RC, Gray JB, Gurnham CF, Jacobs LJ, Klepper RP, Michalson AW, Oldshue JY, Silverblatt CE, Smith JC, Todd DB (1984) Liquid–solid systems. In: Perry RH, Green D (eds) Perry’s chemical engineers’ handbook. McGrow-Hill, Singapore
Misic DM, Sudo Y, Suzuki M, Kawazoe K (1982) Liquid-to-particle mass-transfer in a stirred batch adsorption tank with non-linear isotherm. J Chem Eng Jpn 15(1):67–70
Økland TE, Wilhelmsen E, Solevåg Ø (2005) A study of the priority substances of the Water Framework Directive, monitoring and need for screening. Bergfald & Co., Norway
Otero M, Lopes CB, Coimbra J, Ferreira TR, Silva CM, Lin Z, Rocha J, Pereira E, Duarte AC (2009) Priority pollutants (Hg2+ and Cd2+) removal from water by ETS-4 titanosilicate. Desalination 249(2):742–747
Patzay G (1995) A simplified numerical solution method for the Nernst–Planck multicomponent ion exchange kinetics model. React Funct Polym 27(1):83–89
Pinto NG, Graham EE (1987) Characterization of ionic diffusivities in ion-exchange resins. Ind Eng Chem Res 26(11):2331–2336
Rodriguez JF, Valverde JL, Rodrigues AE (1998) Measurements of effective self-diffusion coefficients in a gel-type cation exchanger by the zero-length-column method. Ind Eng Chem Res 37(5):2020–2028
Rodriguez JF, de Lucas A, Leal JR, Valverde JL (2002) Determination of intraparticle diffusivities of Na+/K+ in water and water/alcohol mixed solvents on a strong acid cation exchanger. Ind Eng Chem Res 41(12):3019–3027
Samson E, Marchand J (1999) Numerical solution of the extended Nernst–Planck model. J Colloid Interface Sci 215(1):1–8
Schiesser WE (1991) The numerical method of lines. Academic Press, USA
Siegel FR (2002) Environmental geochemistry of potentially toxic metals. Springer, Berlim
Silva CM, Lito PF (2007) Application of the Maxwell–Stefan approach to ion exchange in microporous materials. Batch process modelling. Chem Eng Sci 62(23):6939–6946
Slater MJ (1991) Principles of ion exchange technology. Butterworth-Heinemann, Great Britain
Smith TG, Dranoff JS (1964) Film diffusion-controlled kinetics in binary ion exchange. Ind Eng Chem Fundam 3(3):195–200
Treybal RE (1981) Mass-transfer operations. McGraw-Hill International Editions, Singapore
Valverde JL, De Lucas A, Carmona M, Gonzalez M, Rodriguez JF (2004) A generalized model for the measurement of effective diffusion coefficients of heterovalent ions in ion exchangers by the zero-length column method. Chem Eng Sci 59(1):71–79
van der Stegen JHG, van der Veen AJ, Weerdenburg H, Hogendoorn JA, Versteeg GF (1999) Application of the Maxwell–Stefan theory to the transport in ion-selective membranes used in the chloralkali electrolysis process. Chem Eng Sci 54(13–14):2501–2511
Varshney KG, Pandith AH (1999) Forward and reverse ion-exchange kinetics for some alkali and alkaline earth metal ions on amorphous zirconium(IV) aluminophosphate. Langmuir 15(22):7422–7425
Varshney KG, Gupta PA, Tayal N (2003) Kinetics of ion exchange of alkaline earth metal ions on, acrylamide cerium(IV) phosphate: a fibrous ion exchanger. Colloids Surf B Biointerfaces 28(1):11–16
Wesselingh JA, Vonk P, Kraaijeveld G (1995) Exploring the Maxwell–Stefan description of ion-exchange. Chem Eng J Biochem Eng J 57(2):75–89
Acknowledgments
Patrícia F. Lito wishes to thank Fundação para a Ciência e Tecnologia (Portugal) for the Grant (SFRH/BPD/63214/2009) provided for this study.
Author information
Authors and Affiliations
Corresponding author
Appendices
Nomenclature
- \(A\) :
-
External particle surface area (m)
- \({\text{AARD}}\) :
-
Average absolute relative deviation
- \(\left[ B \right]\) :
-
Matrix with MS diffusivities
- \(C_{i}\) :
-
Molar concentration of \(i\) in bulk solution (mol/m3)
- \(d_{\text{p}}\) :
-
Particle diameter (m)
- \(D_{i}\) :
-
Self-diffusion coefficient of species \(i\) (m2/s)
- \(D_{\text{Aw}}\) :
-
Diffusivity of the solute in solution (m2/s)
- \(D_{ij}\) :
-
Interdiffusion coefficient of pair \(i{ - }j\) (m2/s)
- Đ ij :
-
MS surface diffusivity of pair \(i{ - }j\) (m2/s)
- Đ is :
-
MS surface diffusivity of pair \(i\)-fixed ionic charges (m2/s)
- \({\text{F}}\) :
-
Faraday constant (C/mol)
- \(k_{\text{f}}\) :
-
Film mass transfer coefficient (m/s)
- \(K_{\text{LF}}\) :
-
Langmuir–Freundlich parameter
- \([L]\) :
-
\(= [B]^{ - 1}\)
- \(n\) :
-
Langmuir–Freundlich parameter
- \(N_{j}\) :
-
Molar flux of counter ion j (mol/m2 s)
- \(q_{j}\) :
-
Molar concentration of counter ion j in the particle, (mol/m3)
- \(q_{\text{t}}\) :
-
Total concentration of ionic species in the particle (mol/m3)
- \(\bar{q}_{j}\) :
-
Average concentration of j in the particle (mol/m3)
- \(Q\) :
-
Ion exchanger molar capacity (mol/m3)
- \(r\) :
-
Radial position in the particle (m)
- \(Sc\) :
-
Schmidt number
- \(Sh\) :
-
Sherwood number
- \(\Re\) :
-
Gas constant (J/mol K)
- \(R\) :
-
Particle radius (m)
- \(Re\) :
-
Reynolds number
- \(t\) :
-
Time, s (and h in the figures)
- \(T\) :
-
Absolute temperature (K)
- \(u_{i}\) :
-
Velocity of i relative to the solid, (m/s)
- \(V_{\text{L}}\) :
-
Volume of fluid phase (m3)
- \(V_{\text{s}}\) :
-
Volume of solid phase (m3)
- \(x_{i}\) :
-
Molar fraction of i in bulk solution
- \(y_{j}\) :
-
Molar fraction of counter ion j in the particle
- \(z_{i}\) :
-
Charge of component \(i\)
Greek letters
- \(\varepsilon\) :
-
Mixer power input per unit of fluid mass
- \(\gamma_{{i,{\text{sol}}}}\) :
-
Activity coefficient of counter ion \(i\) in a solution in equilibrium with particle
- \(\varphi\) :
-
Electrostatic potential (V)
- \(\left[ \varGamma \right]\) :
-
Matrix of thermodynamic factors
- \(\xi_{i}\) :
-
Related with the electrostatic potential gradient
- \(\nu\) :
-
Kinematic viscosity
- \(\mu_{i}\) :
-
Chemical potential of \(i\) (J/mol)
Subscripts
- A:
-
Counter ion initially present in bulk solution (Cd2+)
- B:
-
Counter ion initially present in particle (Na+)
- S:
-
Fixed charged groups of the particle
- \(\infty\) :
-
Final equilibrium condition of experiment
Rights and permissions
About this article
Cite this article
Lito, P.F., Aniceto, J.P.S. & Silva, C.M. Maxwell–Stefan based modelling of ion exchange systems containing common species (Cd2+, Na+) and distinct sorbents (ETS-4, ETS-10). Int. J. Environ. Sci. Technol. 12, 183–192 (2015). https://doi.org/10.1007/s13762-013-0438-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13762-013-0438-2