Lagrangian decompositions for the two-level FTTx network design problem

Abstract

We consider the design of a passive optical telecommunication access network, where clients have to be connected to an intermediate level of distribution points (DPs) and further on to some central offices (COs) in a tree-like fashion. Each client demands a given number of fiber connections to its CO. Passive optical splitters installed at the DPs allow $k$ connections to share a single common fiber between the DP and the CO. We consider fixed charge costs for the use of an edge of the underlying street network, of a DP, and of a CO and variable costs for installing fibers along the street edges and for installing splitters at the DPs. We present two Lagrangian decomposition approaches that decompose the problem based on the network structure and on the cost structure, respectively. The subproblems are solved using mixed integer programming (MIP) techniques. We report computational results for realistic instances and compare the efficiency of the Lagrangian approaches to the solutions of an integrated MIP model.

Introduction

Motivation In the deployment of passive optical networks (PONs), optical splitters are used to enable a single optical fiber to serve multiple premises. Optical line terminals (OLTs) are placed at the service provider’s central offices (COs) and a number of optical network units (ONUs) is placed either at the location of end users (FTTH deployment) or close to them (FTTC/FTTB deployment). Splitters of different types (e.g., 1:16, 1:32, or 1:64) are placed at the distribution points (DPs) between ONUs and OLTs and several splitters can be aggregated in a single cabinet. A great advantage of PONs compared to point-to-point network architectures is that it reduces the amount of fiber and the overall set-up costs required for serving the end premises. Telecommunication providers are interested in minimizing the investment costs for building a PON, while providing the required services. The main planning task consists of deciding on the location and capacity of ONUs and DPs and the routing paths to lay down the optical fiber, so that the required services are available at the end premises. This problem is of great relevance for the deployment of new generation telecommunication networks. In this paper, we will introduce a new network design problem that we will refer to as the Two-Level FFTx Network Design Problem (2FTTx). This problem captures the most important optimization aspects of the deployment of PONs with a single layer of splitters between ONUs and OLTs. At the same time, our problem simplifies the very complex costs and capacity structure stemming from the modular cable and duct types installed on the links. Rather than assuming that the cable cost of each link is a stepwise increasing function of the number of optical fibers, we linearize those values and assume that a fixed price has to be paid for each single fiber installed on an edge. In terms of cost, we only distinguish between fibers connecting ONUs to DPs and DPs to OLTs to account for the typically different cable and duct configurations used in these subnetworks. We will refer to the end premises as the end customers. A subnetwork containing the routing paths between COs and DPs is called the feeder network (FN), and a subnetwork containing the routing paths between DPs and end customers is called the distribution network (DN). In our setting, we assume that both the feeder network and the distribution network must have tree (or, more precisely, forest) topologies. Although there are no technological reasons for this restriction, this requirement is typically imposed by the network operator for practical reasons. With a tree-like network structure, deployment, upgrade and maintenance of a PON become much simpler and less error-prone in practice. For the same reason, operators usually also forbid to use the same cable (fiber bundle) for both feeder network and distribution network fibers, for fibers heading into different directions, or for fibers heading towards different COs. Figure 1 illustrates an example instance.

Fig. 1

a An example of the input graph. Triangles are customers, squares are potential DPs, pentagons are potential COs and circles are the remaining nodes. Numbers below triangles are customer demands. b A feasible solution. Two COs and three DPs are opened. Numbers next to the DPs are the splitter ratios—one splitter per DP location is installed. Consequently, flow along thick edges is one

Our main goal in this paper is to develop computational methods that enable practitioners to (approximately) solve very large instances of the 2FTTx problem with very little computing time. Such methods are of particular interest in the early stages of the long-term strategic network planning, when numerous planning scenarios with varying technological assumptions and demand, cost, or revenue predictions are evaluated. These are then used to identify the most important parameters and make the global strategic decisions concerning technology vendors, the use of existing or the building of new infrastructures, or the long-term evolution of the network, for example. These case studies require methods that are able to solve the 2FTTx network design problem for very large network regions consisting of several PON areas very fast and with a sufficiently small optimality gap, but not necessarily to optimality. The proposed Lagrangian decomposition approaches perfectly meet these requirements. They are also very useful to quickly compute good bounds and approximate solutions in later planning stages. For the final network and hardware configuration planning, which is typically performed only once for each of the much smaller single PON areas, it is, however, advisable and computationally feasible to use a more accurate model of the various technical elements (such as the different duct and cable types) to fully exploit all potential savings.

Problem definition

More formally, the 2FTTx is defined as follows: We are given an undirected graph $G=(V,E)$ with the set of nodes $V$ partitioned into customers ($V_\mathrm{{C}}$), potential distribution points ($V_\mathrm{{D}}$), potential central offices ($V_\text {CO}$) and the remaining nodes ($V_\mathrm{{O}}$). At least one central office has to be opened, and each customer $v \in V_\mathrm{{C}}$ has to be provided with at least $d_v \ge 0$ fibers. Fiber connections run from a CO, following a path through at least one DP, until they reach an end customer. Splitters are installed at DPs so that every single fiber emanating from a CO can be split into multiple fibers continuing towards customers according to the splitting ratios of the given splitter types. A fiber path emanating from a CO must pass through exactly one splitter at some DP on its way towards a customer. This splitter ’splits’ the path into its feeder sub-path between the CO and the DP where this splitter is located and the distribution sub-path between the DP and the customer. Other DPs that are installed along the fiber path are bypassed by the feeder and the distribution sub-path. Note that we assume the node sets $V_\mathrm{{C}}$, $V_\mathrm{{D}}$, and $V_\text {CO}$ to be disjoint in our input to properly model the different functionalities and costs associated with the elements at ONUs, splitters and OLTs in the considered two-level hierarchy. A network location that may contain a central office or a distribution point or both, for example, is represented by two co-located (and connected) nodes belonging to $V_\mathrm{{C}}$ and $V_\mathrm{{D}}$, respectively. The approach of using different nodes representing the different functionalities that a network location may have is extremely powerful, as it enables practitioners to selectively permit or forbid such combinations depending on the individual location. Also note that (some of the) fibers can simply bypass nodes in $V_\mathrm{{D}}$ or in $V_\mathrm{{C}}$ and $V_\text {CO}$ without being split or without being terminated, respectively.

We consider various capacities and fixed and variable costs related to the setup of the infrastructure and to the installation of fibers and components of the network. Along each edge (trail) $e\in E$, at most $u_e$ fibers can be installed in the feeder network and at most $u_e$ fibers can be installed in the distribution network. The fixed-charge cost for setting up edge $e\in E$ is $c_e$. The cost of installing a single feeder network fiber along edge $e\in E$ is $c_e^f$ and the cost of a single distribution network fiber is $c_e^g$. We assume different costs for feeder and distribution fibers to account for the typically different cable and duct configurations used in these subnetworks in practice.

At the potential distribution point and each central office, we consider the following capacity restrictions and costs. At each CO $v\in V_\text {CO}$, a total number of at most $u_v$ feeder fibers may be terminated. Setting up CO $v\in V_\text {CO}$ induces a fixed cost of $c_v$. As each fiber that emanates from a CO is terminated (or, more precisely, split) by exactly one splitter at some DP, we do not introduce an individual parameter for the cost of terminating a single fiber at a CO. Instead, this cost is included in the cost of the splitter device that necessarily has to be installed at the other end of the fiber.

Similarly, at each DP $v\in V_\mathrm{{D}}$, a total number of at most $u_v$ distribution fibers may be terminated (or, more precisely, connected to a splitter) and setting up $v\in V_\mathrm{{D}}$ costs $c_v$. Using different values for $u_v$ and $c_v$, different classes of DPs, such as street cabinets or underground closures, can be easily modeled. If several classes are possible at the same location, these can be modeled via different co-located nodes in the graph. Let $T$ denote the set of all available splitter types that can be installed in any of the considered potential DPs. For each $t\in T$, let $s_t$ be the splitter ratio. As not all splitter types can be installed in all DPs, given node-dependent upper bounds $J_{t,v}$, $t\in T$ and $v\in \mathrm{{DP}}$, describe how many splitters of which type can be installed at the different potential DPs. The costs of installing one splitter of type $t\in T$ at DP $v\in \mathrm{{DP}}$ is $c_{t,v}$. Recall that this cost also includes the termination cost at the CO for the feeder fiber supplying this splitter.

Our model also permits to limit the number of chosen DPs and COs, which has been of practical interest, especially in multi-period network deployment studies. For this, the input parameters $N_\mathrm{{D}}$ and $N_\text {CO}$ express the maximum total number of allowed DPs and COs, respectively. In the computational experiments reported in this paper, however, these parameters are infinity.

The optimization goal consists of deciding which COs and which DPs to open, which splitters to install at the DPs, and how to route paths in the FN and the DN so that demands of all customers are satisfied at minimum cost. Thereby, DP and CO locations can be traversed as intermediate nodes, in which case, no opening costs need to be paid for them. In addition, even if the feeder and the distribution network both use the same edge, the fixed-charge cost $c_e$ is paid only once. Moreover, FN and DN are required to have tree topologies.

Related Literature. There are several problems studied in the literature that deal with the design of FTTx networks. Connected Facility Location, for example, considers the design of a tree–star network, where facilities (e.g., splitters) are connected to customers in a star-like fashion. There are no splitter- or edge-capacities and fiber costs are discarded, so that the optimization goal consists of determining the network topology that minimizes the facility opening plus edge set-up costs. This problem has been studied in Eisenbrand et al. (2010), Gollowitzer and Ljubić (2011), Leitner and Raidl (2011), to mention a few recent references.

Another related problem that combines network design and facility location aspects is the Two Level Network Design (TLND) problem. In this problem, we are given two technologies and two types of nodes that need to be served by them, and the goal consists of building a tree–tree network such that facilities are installed at the transition points between the two technologies (see Gollowitzer et al. (2013)). In Balakrishnan et al. (1994), the two level network design problem without facilities is studied. The 2FTTx can be seen as a generalization of the TLND problem: if sufficiently large splitter- and edge-capacities are assumed, and the fiber costs are zero, the 2FTTx reduces to the TLND problem.

The Local Access Network Design (LAND) problem is a problem that combines the topological design of the network with the decisions on routing the fibers in order to serve customer demands, while respecting edge capacities (see, e.g., Salman 2000, Putz 2012). This problem captures the capacity aspects of our problem, but assumes that there are no splitters installed on the way between the COs and the end premisses.

Finally, we point out that there are also other works in the literature focusing on other designing aspects of FTTx networks. For example, in recent works presented in Gualandi et al. (2010a), 2010b, Kim et al. (2011), Chardy et al. (2012), the authors concentrate on splitter location and dimensioning aspects by assuming that the routing paths are given and, therefore, can be replaced by assignment arcs.

More practice-oriented approaches have been studied in Martens et al. (2009). Using a two-step approach with suitable mixed integer programming (MIP) formulations, it is possible to optimize fiber-optic networks in realistic scenarios (see Martens et al. 2010). Also Orlowski et al. (2011) conducted various practice-oriented case studies that originated from planning scenarios by a German carrier. Finally, a survey by Grötschel et al. (2013) provides a comprehensive overview on optimization approaches used in the deployment of optical access networks.

Our Contribution. We first propose an integrated MIP model (cf. “MIP model”) and present families of strengthening valid inequalities for it. To deal with the size and complexity of the problem, we then propose two Lagrangian decomposition approaches for solving the 2FTTx (cf. “Lagrangian decomposition into feeder and distribution part” and “Lagrangian decomposition into fixed-charge and flow-cost part”). The first approach decomposes the problem based on the network structure and the second approach decomposes the problem based on the cost structure. The subproblems are solved using MIP techniques. A combination of Lagrangian heuristics (presented in “Lagrangian Framework and Heuristics”) and MIP techniques allows us to solve some of the real-world network planning instances within a few percent of optimality. Detailed computational results are shown in “Computational results”.

MIP model

Let $A$ be the set of arcs obtained by bidirecting edges from $E$. We will use binary variables $x_v \in \{0,1\}$ for each $v \in V_\mathrm{{D}}$ to indicate whether splitters are installed at location $v$ or not. Similarly, binary variables $z_v \in \{0,1\}$ will indicate whether a central office $v \in V_\text {CO}$ is opened or not. The number of splitters of type $t$ installed at the DP location $v \in V_\mathrm{{D}}$ will be counted using integer variables $y_{t,v}$. Finally, for each edge $e \in E$, binary variables $w_e$ will indicate whether the edge $e$ is used or not, and the number of fibers in the DN and the FN installed along arc $a\in A$ is counted using variables $g_a$ and $f_a$, respectively. Using these variables, our objective function can be described as follows:

Objective function

$$\begin{aligned} \min \; \sum _{v \in V_\text {CO}} c_v z_v + \sum _{v \in V_\mathrm{{D}}} c_v x_v + \sum _{e \in E} c_e w_e + \sum _{v \in V_\mathrm{{D}}} \sum _{t \in T} c_{t,v} y_{t,v} + \sum _{a \in A} ( c_a^\text {f} f_a + c_a^\text {g} g_a ) \end{aligned}$$

The first two terms are the installation costs for COs and DPs, followed by the installation costs for the edges, followed by the splitter installation costs. The last summation corresponds to the total fiber costs installed in the DN and the FN.

Bounds on splitter installations, DPs and COs. The bounds regarding the total number of allowed DPs and COs are expressed using constraints (1) and (2), respectively, and the bounds regarding the maximal number of splitters of type $t$ at the DP node $v$ are expressed using (3):

$$\begin{aligned} \sum _{v \in V_\mathrm{{D}}} x_v&\!\!\!\!\! \le N_\mathrm{{D}} \end{aligned}$$

(1)

$$\begin{aligned} \sum _{v \in V_\text {CO}} z_v&\!\!\!\! \le N_\text {CO} \end{aligned}$$

(2)

$$\begin{aligned} y_{t,v}&\le J_{t,v} x_v&v \in V_\mathrm{{D}}, t \in T \end{aligned}$$

(3)

Each splitter installed at a DP location requires a single fiber from a CO (where a transceiver needs to be placed). The overall number of splitters installed at a DP determines its upstream-fiber demand. The overall number of fibers available in the DN and obtained after splitting at a certain DP location determines its downstream-fiber supply. Before we present the remaining constraints of our MIP model, we introduce auxiliary variables that help simplify the notation:

$$\begin{aligned} \begin{array}{l@{\quad }l@{\quad }l} F_v \in \mathbb Q &{} \forall v \in V_\mathrm{{D}} &{} \hbox {the number of upstream-fibers at the DP} v \\ G_v \in \mathbb Q &{} \forall v \in V_\mathrm{{D}} &{} \hbox {the number of downstream-fibers at the DP} v \\ H_v \in \mathbb Q &{} \forall v \in V_\text {CO}&{} \hbox {the number of transceivers installed at the CO} v\\ w^f_{a} \in \{0,1\} &{} \forall a \in A &{} 1\,\hbox {if the arc}\,a\,\hbox {is used by the}\,f{\hbox {-flow}} \\ w^g_{a} \in \{0,1\} &{} \forall a \in A &{} 1\,\hbox {if the arc}\,a\,\hbox {is used by the}\,g{\hbox {-flow}} \\ \end{array} \end{aligned}$$

Flow conservation in distribution and feeder network. To ensure a feasible routing in the DN, the following flow-preservation constraints (4) are used. They also state that the total customer demand has to be satisfied using the supply of the downstream fibers that are available at distribution points. Constraints (5) and (6) make sure that the $g$-flow is routed along $e$ only if the edge $e$ is installed.

$$\begin{aligned} \sum _{a \in \delta ^-(v)} g_a - \sum _{a \in \delta ^+(v)} g_a \;&= \left\{ \begin{array}{l@{\quad }l} d_v &{} ~ v \in V_\mathrm{{C}} \\ -G_v &{} ~ v \in V_\mathrm{{D}} \\ 0 &{} ~ \text {else} \end{array} \right. \qquad v \in V \end{aligned}$$

(4)

$$\begin{aligned} g_{ij}&\le u_ew^g_{ij} \quad \quad (i,j) \in A \end{aligned}$$

(5)

$$\begin{aligned} w^g_{ij} + w^g_{ji}&\le w_e \quad \qquad ~\, \{i,j\} \in E \end{aligned}$$

(6)

At the first glance, variables $w^g_a$ can be omitted. However, they are used later on to derive cuts that will strengthen the LP relaxation.

To make sure that the routing between COs and DPs is feasible, we consider constraints (7). These constraints also make sure that the overall upstream-demand at distribution points (expressed using $F_v$ variables) is to be satisfied by installing a sufficient number of transceivers at the corresponding COs ($H_v$ variables). Constraints (8) and (9) make sure that the $f$-flow is routed along $e$ only if the edge $e$ is installed.

$$\begin{aligned} \sum _{a \in \delta ^-(v)} f_a - \sum _{a \in \delta ^+(v)} f_a \;&= \left\{ \begin{array}{l@{\quad }l} F_v &{} ~ v \in V_\mathrm{{D}} \\ -H_v &{} ~ v \in V_\text {CO}\\ 0 &{} ~\text {else} \end{array} \right. \qquad v \in V \end{aligned}$$

(7)

$$\begin{aligned} f_{ij}&\le u_ew^f_{ij}\quad \quad (i,j) \in A \end{aligned}$$

(8)

$$\begin{aligned} w^f_{ij} + w^f_{ji}&\le w_e \quad \qquad ~\, \{i,j\} \in E \end{aligned}$$

(9)

Notice that in this model, since $f$ ($g$) is a single commodity flow, the flows of the opposite directions cancel out. However, it might happen that along an edge $e=\{i,j\}$, $f$ sends flow in direction $(i,j)$ and $g$ sends flow in direction $(j,i)$ (see Fig. 1b where this happens along the edge $\{u,v\}$).

Moreover, the tree topologies of FN and DN are guaranteed using the following in-degree constraints:

$$\begin{aligned} \sum _{a \in \delta ^-(i)} w^f_a&\le 1,&\quad i\in V \end{aligned}$$

(10)

$$\begin{aligned} \sum _{a \in \delta ^-(i)} w^g_a&\le 1,&\quad i\in V \end{aligned}$$

(11)

Upstream-demand and downstream-capacity at DPs. For each installed splitter at a DP $v \in V_\mathrm{{D}}$, a single fiber in the FN is required, and the total upstream-demand at $v$ is calculated using constraints (12). The number of downstream-fibers available at the DP $v$ is bounded by the total number of installed splitters and their capacity, see (13):

$$\begin{aligned} F_v&= \sum \limits _{t \in T} y_{t,v}\quad \quad v\in V_\mathrm{{D}} \end{aligned}$$

(12)

$$\begin{aligned} G_v&\le \sum _{t \in T} s_t y_{t,v}\quad v \in V_\mathrm{{D}} \end{aligned}$$

(13)

Note that these constraints link the distribution network and the feeder network. The total flow arriving at the customer nodes in the distribution network can never exceed the flow into the distribution points, except by factors introduced by the splitting ratios of the splitters available in the model.

Finally, the number of available downstream fibers at DPs and COs $v$ is also bounded by $u_v$, i.e.,:

$$\begin{aligned} G_v&\le u_v x_v&\quad v \in V_\mathrm{{D}} \end{aligned}$$

(14)

$$\begin{aligned} H_v&\le u_v z_v&\quad v \in V_\text {CO} \end{aligned}$$

(15)

Without loss of generality, we assume that $u_v \le \sum _{t\in T}s_tJ_{t,v}$.

The set of feasible 2FTTx solutions is completely described using constraints (1)–(15). This MIP model will be called the aggregated MIP model. It contains a large number of variables and constraints and, therefore, it is quite unrealistic that using this model one will be able to solve instances arising in the practical application. Besides, the lower bounds obtained by this model may be quite weak, due to involved “bigM”-constraints: (5), (8), (14), (15). To overcome the problems with the weak lower bounds, in the following subsection, we will first present families of strengthening valid inequalities. In the second half of the paper, to deal with the size and complexity of the problem, we will propose two Lagrangian decomposition approaches. These will enable us to solve some of the real-world network planning instances very close to optimality.

Valid inequalities for the aggregated MIP model

Connectivity constraints

Connectivity constraints in the DN. We observe that the flow conservation constraints (4) together with the capacity constraints (5) define a single-commodity flow problem in the distribution network. For the problem to be feasible, for each customer $v\in V_\mathrm{{C}}$, $d_v$ units of flow need to be transported from a distribution point with $x_k=1$ to $v$. This also implies that the distribution network has to be connected. The following connectivity constraints in the DN are, therefore, valid for our problem. Solutions to the problem have to fulfill them for every node subset $W$ that contains at least one customer node.

$$\begin{aligned} \sum _{k \in W \cap V_\mathrm{{D}}} x_k + \sum _{(i,j) \in \delta ^-(W)} w^g_{ij} \ge 1 \quad W \subset V, W \cap V_\mathrm{{C}} \ne \emptyset \end{aligned}$$

(16)

Here, $W$ is an arbitrary node subset that contains at least one customer node. These constraints basically state that for each customer $i$ there has to exist an open DP $k$ such that they can be connected by a directed path from $k$ to $i$ in the subgraph of $G$ induced by $w^g$ variables. These inequalities are not implied by the previous model and can be used to strengthen the LP bounds (see, e.g., Ljubić et al. 2012).

Connectivity constraints in the FN. Similarly, the flow conservation constraints (7) together with the capacity constraints (8) define a single-commodity flow problem in the feeder network. For the problem to be feasible, for each DP $k\in V_\mathrm{{D}}$, $F_k$ flow units need to be transported from a central office with $z_\ell =1$ to $k$. As above, the following connectivity constraints in the FN are, therefore, valid. Solutions to the problem have to fulfill them for every node subset $W$ that contains at least one distribution point:

$$\begin{aligned} \sum _{\ell \in W \cap V_\text {CO}} z_\ell + \sum _{(i,j) \in \delta ^-(W) } w^f_{ij} \ge x_k \quad W \subset V, k \in W \cap V_\mathrm{{D}} \end{aligned}$$

(17)

They ensure that open COs and open DPs belong to a connected network, and even more, that for each open DP $k$ there has to exist an open CO $\ell$ such that they can be connected by a directed path from $\ell$ to $k$ in the subgraph of $G$ induced by $w^f$ variables. Also these inequalities are not implied by the previous model and can be used to strengthen the LP bounds.

Global connectivity constraints. These constraints are based on the observation that the overall solution has to be connected. Furthermore, since the edges $e \in E$ can be oriented in one or the other direction, and the costs for the installation are paid only once, no matter if the same edge is used twice (once in the FN, and once in the DN), the following directed connectivity cuts are valid and are not implied by the previously introduced cuts. Solutions to the problem have to fulfill them for every node subset $W$ that contains at least one customer node:

$$\begin{aligned} \sum _{\ell \in W \cap V_\text {CO}} z_\ell + \sum _{(i,j) \in \delta ^-(W)} w^f_{ij} \ge 1 \quad W \subset V, W \cap V_\mathrm{{C}} \ne \emptyset \end{aligned}$$

(18)

These inequalities make sure that for each customer $i \in V_\mathrm{{C}}$ there is a directed path between an open CO $\ell$ and $i$ in the subgraph induced by $w^f$ variables. That way, the variables $w^f$ that are originally intended to model only the arcs of the FN are used to “push-up” the capacities of fractional edge variables in the DN.

Lemma 1

Constraints (16), (17) and (18) can be separated in polynomial time.

proof

We will explain how to separate (16), the remaining separation algorithms follow the same idea. Given the values $\tilde{x}$ and $\tilde{w}^g$ of a fractional LP solution to the aggregated MIP, we can separate constraints (16) in an auxiliary graph $G_g=(V_g,A_g)$ that is generated as follows. Artificial root node $r$ is added to $V$ and connected to all distribution points $v\in V_\mathrm{{D}}$, i.e., $V_g = \{r\} \cup V , A_g = A \cup {(r,k) \mid k \in V_\mathrm{{D}}}$. In the resulting digraph $G_g$, for each $v\in V_\mathrm{{C}}$, there has to be a flow of value not less than 1 from $r$ to $v$. We treat the values of $\tilde{w}^g_{ij}$ as the capacity on the arc $(i,j)$ and $\tilde{x}_k$ as capacity on the arc $(r,k)$. If the value of the maximum flow is less than one, the associated minimum cut, projected into the space of $x$ and $w^g$ variables, corresponds to a violated  (16) inequality. $\square$

In the following, let

$$\begin{aligned} \mathcal{G}&:= \bigl \{ (g,G,w^g\!,w) \in \mathbf R _+^{|A|+|V_\mathrm{{D}}|}\times \{0,\!1\}^{|A|+|E|} \mid \nonumber \\&(g,G,w^g\!,w)\,\text {satisfies~(4)--(6), (11), (16)} \bigr \}, \quad \text {and} \end{aligned}$$

(19)

$$\begin{aligned} \mathcal{F}&:= \bigl \{ (f,H,F,w^f\!,w) \in \mathbf R _+^{|A|+|V_\text {CO}|+|V_\mathrm{{D}}|}\times \{0,\!1\}^{|A|+|E|} \mid \nonumber \\&(f,\!H,F,w^f\!,\!w) \text { satisfies (7)--(9), (10), (17)}\bigr \}. \end{aligned}$$

(20)

The following section illustrates how the problem can be decomposed in an intuitive way, so that the subproblems associated with $\mathcal G$ and $\mathcal F$ can be treated separately.

Lagrangian decomposition into feeder and distribution part

Our first Lagrangian decomposition approach decomposes the problem in the most intuitive way: the design of the FN and the design of the DN. To obtain this decomposition, we have to relax constraints that couple both networks. We proceed as follows:

• 1. Duplicate $y_{t,v}$ variables: introduce a copy of $y_{t,v}$ variables (denoted by $y'_{t,v}$) and then replace $y_{t,v}$ by $y'_{t,v}$ in equations (12).

• 2. Duplicate $x_v$ variables: Introduce a copy denoted by $x'_v$.

• 3. Duplicate $w_e$ variables: Introduce a copy denoted by $w'_e$.

• 4. Extend the previous model with the following inequalities, associate dual variables $\lambda$, $\alpha$ and $\beta$ to them and relax them in a Lagrangian fashion:

  $$\begin{aligned} \begin{array}{rll@{\quad }l} \sum _{t\in T} y'_{t,v} &{} \ge \sum _{t \in T} y_{t,v} &{} \qquad v\in V_\mathrm{{D}} &{} \ldots (\lambda _v) \\ w_e &{} = w'_e &{} \qquad e\in E &{} \ldots (\alpha _e) \\ x_v &{} = x'_v &{} \qquad v\in V_\mathrm{{D}} &{} \ldots (\beta _v) \end{array} \end{aligned}$$

The whole problem decomposes into two subproblems that will be referred to as the Feeder Problem (F) and the Distribution Problem (D). Figure 2 illustrates this decomposition.

Fig. 2

Lagrangian decomposition into the feeder and distribution part: a distribution network (DN), and b feeder network (FN)

The Feeder Network Problem

After substituting $F_v := \sum _{t\in T} y'_{t,v}$, for each $v \in V_\mathrm{{D}}$, and adding back constraints (3), the feeder network subproblem is given as:

$$\begin{aligned} (\mathrm{F}) \quad \min \sum _{v \in V_\text {CO}} c_v z_v&- \sum _{v \in V_\mathrm{D}}\lambda _vF_v + \sum _{a \in A} c_a^\text {f} f_a- \sum _{v\in V_\mathrm{D}}\beta _vx'_v - \sum _{e \in E}\alpha _{e} w'_{e} \nonumber \\ H_v&\le u_v z_v \qquad \qquad \qquad v \in V_\text {CO} \end{aligned}$$

(21)

$$\begin{aligned} F_v&\le \sum _{t\in T} J_{t,v}x'_v \qquad \quad \, v\in V_\mathrm{{D}} \end{aligned}$$

(22)

$$\begin{aligned} \sum _{v \in V_\text {CO}} z_v&\le N_\text {CO} \end{aligned}$$

(23)

$$\begin{aligned} (z,x')&\in \{0,1\}^{|V_\text {CO}|+ |V_\mathrm{{D}}|}, \; (f, H, F,w^f,w') \in \mathcal{F} \end{aligned}$$

The Distribution Network Problem

$$\begin{aligned} \mathrm{{(D)}} \; \min \! \sum _{v \in V_\mathrm{{D}}} \!\! (c_v\! +\! \beta _v) x_v + \sum _{e \in E} (c_e\! +\! \alpha _{e}) w_{e} + \!\sum _{v \in V_\mathrm{{D}}}\sum _{t \in T}(c_{t,v} \!+\!\lambda _v) y_{t,v}+ \sum _{a \in A} c_a^\text {g} g_a \end{aligned}$$

$$\begin{aligned} G_v&\le \min \{ u_v x_v, \sum _{t \in T} s_t y_{t,v} \} v \in V_\mathrm{{D}} \qquad \end{aligned}$$

(24)

$$\begin{aligned} y_{t,v}&\le J_{t,v} x_v \quad \quad \quad \quad \quad v \in V_\mathrm{{D}} \end{aligned}$$

(25)

$$\begin{aligned} \sum _{v \in V_\mathrm{{D}}} x_v&\le N_\mathrm{{D}} \end{aligned}$$

(26)

$$\begin{aligned} (x,y) \in \{0,1\}^{|V_\mathrm{{D}}|}&\times&\mathbb Z _+^{|T||V_\mathrm{{D}}|}, \; (g,G,w^g,w) \in \mathcal{G} \end{aligned}$$

Observe that both problems, (F) and (D) are NP-hard. However, they are structurally significantly simpler than the starting problem and, therefore, easier to solve from the practical perspective. The problems are generalizations of the capacitated network design problem with single source. We solve these problems using a branch-and-cut (B&C) approach whose main ingredients are outlined in “Computational results”. One of the advantages of the B&C approaches is that warm start features (i.e., initializations of upper bounds and valid inequalities) can be re-used from iteration to iteration (via solution pools and cut pools, respectively).

When solving this decomposition, we extend the model (F) with the global connectivity cuts (18) that make sure that customers are connected with open COs. These constraints restrict the set of feasible solution for the (F) model, but they do not cut off global optimal solution(s). In addition, these constraints strengthen the Lagrangian bounds obtained by this decomposition. Finally, to make sure that global connectivity cuts are also associated with edge set-up costs, Lagrangian multipliers are initialized as $\alpha _e := -c_e$, for all $e \in E$. The remaining Lagrangian multipliers are initialized with zero values. We will refer to this decomposition as the “(F) + (D)” decomposition approach.

Lagrangian decomposition into fixed-charge and flow-cost part

In this section, we propose an alternative Lagrangian decomposition approach in which we decompose the problem according to the classification of variables by cost types. In other words, we decompose the problem into:

• 1. the Fixed Charge Subproblem, which captures all set-up costs associated with fixed-charge variables, $w_e$, $x_v$ and $z_v$, and

• 2. the Flow Subproblem, which captures all variable (flow) costs associated with splitter-installation variables $y_{t,v}$ and flow variables $f_a$ and $g_a$.

Fig. 3

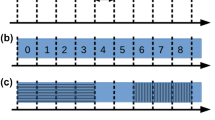
Lagrangian decomposition into a fixed cost, and b variable cost part for the input instance given in Fig. 1 (but here we assume that all customer demands are equal to 32). Thick dashed lines show the $g$-flow, continuous lines show the f-flow. One unit of f-flow is sent along each arc in the FN, and 32 units of flow are sent along each arc in the DN, except between DP $i$ and customer $j$, where g-flow is equal to 64

To the constraints that contain variables of both types, we associate dual variables $\lambda$, $\mu$ and $\nu$, and relax them in Lagrangian fashion:

$$\begin{aligned} \begin{array}{ll@{\quad }ll} y_{t,v} &{} \le J_{t,v}x_v &{} ~ t\in T, v\in V_\mathrm{{D}} \quad &{} \quad \quad \dots (\lambda _{t,v}) \\ G_v &{} \le u_v x_v &{} ~ v \in V_\mathrm{{D}} \quad &{} \quad \quad \dots ( \mu _v) \\ H_v &{} \le u_v z_v &{} ~ v \in V_\text {CO}\quad &{} \quad \quad \dots (\mu _v) \\ g_{ij} &{}\le u_ew^g_{ij} &{} ~ \{i,j\} \in E \quad &{} \quad \quad \dots (\nu ^g_a) \\ f_{ij} &{}\le u_ew^f_{ij} &{} ~ \{i,j\} \in E \quad &{} \quad \quad \dots (\nu ^f_a) \end{array} \end{aligned}$$

Figure 3 illustrates this decomposition approach. We obtain two subproblems, that we will refer to as the Fixed Charge Subproblem (FC) and the Flow Subproblem (FP).

The Fixed Charge Subproblem (FC)

The subproblem that captures the fixed costs of the 2FTTx is given as follows:

$$\begin{aligned} (\mathrm FC ) \quad \min \sum _{v \in V_\text {CO}} (c_v-\mu _vu_v) z_v&+ \sum _{v\in V_\mathrm{{D}}} (c_v-\left( \sum _{t\in T}\lambda _{t,v}J_{t,v}+\mu _vu_v)\right) x_v\nonumber \\&+\sum _{e\in E}c_ew_e - \sum _{a\in A}u_a \left( \nu _a^fw^f_{a}+\nu _a^gw^g_{a}\right) \sum _{v \in V_\mathrm{{D}}} x_v \le N_\mathrm{{D}} \end{aligned}$$

(27)

$$\begin{aligned} \sum _{v \in V_\text {CO}} z_v&\le N_\text {CO}\end{aligned}$$

(28)

$$\begin{aligned} w^f_{ij} + w^f_{ji}&\le w_e \qquad e = \{i,j\}\in E \end{aligned}$$

(29)

$$\begin{aligned} w^g_{ij} + w^g_{ji}&\le w_e \qquad e = \{i,j\}\in E \end{aligned}$$

(30)

$$\begin{aligned} \sum _{a \in \delta ^-(i)} w^f_a&\le 1\qquad i\in V \end{aligned}$$

(31)

$$\begin{aligned} \sum _{a \in \delta ^-(i)} w^g_a&\le 1\qquad i\in V \end{aligned}$$

(32)

$$\begin{aligned} (x,z,w,w^f,w^g)&\in \{0,1\}^{|V_\mathrm{{D}}|+|V_\text {CO}| + |E| + 2|A|} \end{aligned}$$

The Flow Subproblem (FP)

The other subproblem, that captures the variable costs of the 2FTTx, is:

$$\begin{aligned}&\mathrm{{(FP)}} \quad \min \sum \limits _{v\in V_\mathrm{{D}}}\sum \limits _{t\in T} (c_{t,v}+ \lambda _{t,v})y_{t,v} + \sum \limits _{v\in V_\mathrm{{D}}}\mu _vG_v + \sum \limits _{V\in V_{CO}}\mu _vH_v \\&\quad + \sum \limits _{a \in A} (c_a^\text {f} + \nu ^f_a)f_a + \sum \limits _{a \in A} (c_a^\text {g} + \nu ^g_a)g_a \end{aligned}$$

$$\begin{aligned} \sum _{a \in \delta ^-(v)} g_a - \sum _{a \in \delta ^+(v)} g_a \;&= \left\{ \begin{array}{ll} d_v &{} \quad v \in V_\mathrm{{C}} \\ -G_v &{} \quad v \in V_\mathrm{{D}} \\ 0 &{} \quad v \in V_\text {CO}\cup V_\mathrm{{O}} \end{array} \right. \qquad \, v \in V \end{aligned}$$

(33)

$$\begin{aligned} \sum _{a \in \delta ^-(v)} f_a - \sum _{a \in \delta ^+(v)} f_a \;&= \left\{ \begin{array}{ll} F_v &{} \quad v \in V_\mathrm{{D}} \\ -H_v &{} \quad v \in V_\text {CO}\\ 0 &{} \quad v \in V_\mathrm{{C}} \cup V_\mathrm{{O}} \end{array} \right. \quad \qquad v \in V \end{aligned}$$

(34)

$$\begin{aligned} F_v&= \quad \sum _{t\in T}y_{t,v} \qquad \qquad \qquad \qquad \qquad \quad v\in V_\mathrm{{D}} \end{aligned}$$

(35)

$$\begin{aligned} G_v&\le \sum _{t \in T} s_t y_{t,v} \qquad \qquad \qquad \qquad \qquad \quad v \in V_\mathrm{{D}} \end{aligned}$$

(36)

$$\begin{aligned} (f,g,F,G,H,y)&\in \left( \mathrm R _+^{2|A|+2|V_\mathrm{{D}}|+|V_\text {CO}|}, \mathrm Z _+^{|T||V_\mathrm{{D}}|}\right) \end{aligned}$$

Observe that (FC) is a trivial subgraph selection problem. Edge selections can simply be made by the sign of the coefficient. Similarly, we can simply select the nodes with the largest negative coefficients until reaching the bounds on the total number of DPs and COs. Obviously, there is not much gain if the problem is decomposed into one hard and one trivial subproblem. To strengthen the models, we insert the connectivity constraints (16)–(18) in the original MIP model. After the Lagrangian relaxation, these end up in the (FC) subproblem. That way, we end up with a non-trivial subproblem (FC) which makes this decomposition approach useful.

Despite the fact that also in this decomposition both subproblems, (FC) and (FP), are NP-hard, they are significantly simpler than the original problem. The problem (FP) is NP-hard since the packing subproblem has to be solved at each of the installed distribution points. After adding the connectivity constraints, the problem (FC) becomes NP-hard, since it assembles the structure of the cardinality constrained Steiner arborescence problem with node and arc weights. To solve the subproblem (FC), we develop a branch-and-cut algorithm (see “Computational results”) in which solution- and cut-pools are used as warm start features. The subproblem (FP) is solved as a compact MIP model by a black-box MIP solver with an additional advantage that solution pools are used to initialize starting solutions in each Lagrangian iteration. We will refer to this decomposition as the “(FC) + (FP)” decomposition.

Further valid inequalities

When solving the (FC) subproblem, notice that the only way more than one DP/CO is opened is if the costs of the DPs/COs become negative due to the setting of the corresponding dual multipliers. Therefore, the bounds obtained by solving the (FC) subproblem can further be strengthened by additional inequalities that make sure that the capacity of open DPs/COs is sufficient to service customer demands. These inequalities can also reduce the number of iterations of the Lagrangian decomposition. The following inequalities are used for this purpose:

$$\begin{aligned} \sum _{v\in V_\mathrm{{D}}} u_vx_v&\ge \sum _{v\in V_\mathrm{{C}}}d_v \end{aligned}$$

(37)

$$\begin{aligned} \sum _{v\in V_\text {CO}} \left\{ \max _{t\in T}s_t\right\} u_vz_v&\ge \sum _{v\in V_\mathrm{{C}}}d_v \end{aligned}$$

(38)

$$\begin{aligned} \sum _{v\in V_\text {CO}}u_vz_v+\sum _{v\in V_\mathrm{{D}}}x_v\sum _{t\in T}(s_t-1)J_{t,v}&\ge \sum _{v\in V_\mathrm{{C}}}d_v \end{aligned}$$

(39)

Constraints (37) make sure that a sufficient number of downstream fibers is provided, and constraints (38) make sure that a sufficient number of transceivers is installed at COs, so that customer demands can be satisfied (assuming the highest possible splitting ratio). Finally, constraints (39) combine the latter two using the fact that each splitter requires exactly one fiber coming from a CO (and therefore we have $s_t-1$ in the second summation).

Strengthening by splitter-counting

One could aggregate variables $y_{t,v}$ as follows:

$$\begin{aligned} \sum _{v\in V_{DP}}y_{t,v} = y_t \qquad t \in T \end{aligned}$$

These newly introduced integer variables $y_t$ count the number of splitters of type $t \in T$ installed across all DPs. Adding the latter equality into the aggregated MIP brings no benefits; however, in the context of our second Lagrangian relaxation, it helps in solving the (FC) subproblem. After associating dual multipliers $\pi _t$ and relaxing these constraints, the new variables are added to (FC) and an additional term of $-\sum _{t \in T} \pi _ty_t$ is added in the objective function.

Then, the following inequalities are used to further strengthen the (FC) subproblem:

$$\begin{aligned} \sum _{t\in T} s_ty_t&\ge \sum _{v\in V_\mathrm{{C}}}d_v \end{aligned}$$

(40)

$$\begin{aligned} \sum _{v\in V_\text {CO}}u_vz_v+\sum _{t\in T}(s_t-1)y_t&\ge \sum _{v\in V_\mathrm{{C}}}d_v\end{aligned}$$

(41)

$$\begin{aligned} \sum _{v\in V_\mathrm{{D}}} J_{t,v}x_v&\ge y_t\quad \forall t\in T \end{aligned}$$

(42)

$$\begin{aligned} \sum _{v\in V_\text {CO}} u_vz_v&\ge \sum _{t\in T}y_t \end{aligned}$$

(43)

Constraint (40) states that at least as many fibers have to leave the distribution points into the distribution network as are needed to fulfill the total demand.

The first term of (41) is an upper bound on the number of fibers leaving the central offices. The next term counts precisely how many fibers are added to this number by splitting at the distribution points. So the left-hand side is an upper bound on total flow number of the distribution network. The inequality states that this upper bound needs to exceed the total demand or the solution will not be feasible.

The left-hand side of (42) upper-bounds the total number of splitters of a fixed type that can be installed in the network. The inequality states that we need to open at least $\lceil \frac{y_t}{J_{t,v}}\rceil$ distribution points to install $y_t$ splitters of type $t$ without violating the splitter installation bounds.

Finally, (43) states that enough central offices have to be opened to be able to supply all installed splitters with fibers from the feeder network.

Lagrangian framework and heuristics

In this section, we first describe the generic Lagrangian decomposition framework that is applied to both approaches. In this framework, lower bounding and upper bounding procedures are incorporated. Lower bounding procedures are based on solving lower bounds of associated MIP models, and upper bounding procedures are heuristics that we describe below. For each of the proposed decomposition approaches, we develop appropriate heuristics. They solve each of the subproblems independently, using the current Lagrangian multipliers in the objective function. Hence, in all the following heuristics, solving the subproblem always refers to the Lagrangian-modified objective functions, unless it is stated differently.

Generic Lagrangian framework

Relaxing the constraints linking the feeder and the distribution network part as described in “Lagrangian decomposition into feeder and distribution part”, we obtain the Lagrangian function

$$\begin{aligned} L(\Lambda ) := L_\mathrm{{F+D}}(\Lambda ) = L_\mathrm{{F}}(\Lambda ) + L_\mathrm{{D}}(\Lambda ), \end{aligned}$$

where $\Lambda :=(\lambda ,\alpha ,\beta )\in \mathbb R _+^{|V_\mathrm{{D}}|}\times \mathbb R ^{|E|}\times \mathbb R ^{|V_\mathrm{{D}}|}$ is the vector of Lagrangian dual multipliers for the (in)equalities linking the variables $y$, $w$, and $x$ to their copies $y'$, $w'$, and $x'$, respectively. The two functions $L_\mathrm{{F}}(\Lambda )$ and $L_\mathrm{{D}}(\Lambda )$ yield the optimal solution value of the two integer linear problems (F) (augmented with global connectivity cuts (18)) and (D), respectively, for the given dual multipliers $\Lambda$.

Analogously, the decomposition into fixed charge and flow cost-dependent variables described in “Lagrangian decomposition into fixed-charge and flow-cost part” yields the Lagrangian function

$$\begin{aligned} L(\Lambda ) := L_{FC+FP}(\Lambda ) = L_{FC}(\Lambda ) + L_{FP}(\Lambda ), \end{aligned}$$

with dual multipliers $\Lambda :=(\lambda ,\mu ,\nu ,\pi )\in \mathbb R _+^{|V_\mathrm{{D}}||T| + |V_\mathrm{{D}}| + |T| +|V_{CO}| + 2|E|}$ (assuming we introduce the extra splitter count variables $y_t$ as described in “Further valid inequalities”). Here, $L_\mathrm{{FC}}(\Lambda )$ represents the optimal solution value of (FC) after adding constraints (16)–(18) and (37)–(43), while $L_\mathrm{{FP}}(\Lambda )$ represents the optimal solution value of (FP).

It is well known that for each dual vector $\Lambda$, the value $L(\Lambda )$ is a lower bound for the optimal value of original aggregated model (1)–(15) and, hence, also $L^*:=\max _{\Lambda } L(\Lambda )$ is a valid lower bound. As there are only finitely many (basic) solutions to the original model and to each of the subproblems (D), (F), (FC), and (FP), the corresponding dual functions $L_\mathrm{{F}}$, $L_\mathrm{{D}}$, $L_\mathrm{{FC}}$ and $L_\mathrm{{FP}}$ are piece-wise linear and concave in $\Lambda$. Hence, convex function optimization techniques can be applied to find dual multipliers $\Lambda ^*$ that yield the best possible lower bound $L^*$.

In our implementation, we employ a bundle method. Bundle methods typically converge relatively fast requiring only a few evaluations of the dual function(s), which is very attractive in our application, where each evaluation (in principle) requires the solution of an integer linear program. Furthermore, they permit the use of an independent bundle of subgradients for each of the two sub-functions $L_\mathrm{{F}}$ and $L_\mathrm{{D}}$ or $L_\mathrm{{FC}}$ and $L_\mathrm{{FP}}$ involved in the respective Lagrangian function, potentially leading to a further reduction in (sub-)function evaluations. Finally, general purpose implementation of these methods is available, such as ConicBundleHelmberg (2012), Helmberg and Kiwiel (2002), which has already proved its practicability and efficiency in the solution of large scale problems (see, e.g., Helmberg 2009).

The basic theory of bundle methods is explained in Hiriart-Urruty and Lemaréchal (1993) and Bonnans et al. (2003), for example. In principle, given a starting point for the dual multipliers, the bundle method iteratively determines the next candidate as an optimizer of a quadratic model with the current point as a stability center and (dual) constraints stemming from a set (bundle) of previous optimal solutions. If the value of the optimal solution of this quadratic model improves sufficiently over the value at the stability center, the method performs a descent step and proceeds. Otherwise a null step not changing the stability center but improving the quadratic model with the new subgradient is performed.

For the initial dual multipliers and after each descent step of the bundle algorithm, we apply one of the heuristics described in the following sections to compute feasible primal solutions for the overall problem.

To reduce the run time of the two proposed Lagrangian relaxation approaches in practice, we also decided to avoid the solution of the integer linear programs (F), (D), (FC), and (FP) via branch-and-bound in the evaluation of the corresponding (sub-)functions. Instead, we stop after processing the root node of the corresponding branch-and-bound trees. Conceptually, this also can be regarded as the solution of an (appropriately defined) linear relaxation of the respective subproblems, namely a relaxation that includes all those constraints that are implicitly enforced via the simple preprocessing techniques and cutting planes of the ILP solver at the root node and that relaxes all other integrality constraints. Unfortunately, however, it was necessary to disable most of the heuristic preprocessing and cutting plane generation techniques that are implemented in the ILP solver to avoid inconsistencies in their application and resulting numerical instabilities in the bundle algorithm. The resulting bounds will, of course, be weaker than those that can be obtained by optimally solving the integer programming subproblems. Yet, the bounds are very satisfactory from a practical point of view.

Lagrangian heuristic for the (F) + (D) decomposition

For the first decomposition approach, we develop a heuristic that we refer to as the Feeder-Distribution-Feeder Heuristic. Pseudo-code of this heuristic is given in Algorithm 1. The heuristic consists of three stages: in the first stage we solve the feeder subproblem (F) extended by global connectivity cuts (18). That way, we obtain a preliminary topology of our network that makes sure that all customers are connected to each other and to at least one open CO. In the second stage, the edges of this network are used “for free” (cf. Step 1) for solving the distribution subproblem. The last stage is a transition from the distribution subproblem into the feeder subproblem. Solution of (D) is denoted by $S_D$. Edges that belong to $S_D$ are now taken in the solution of (F). In addition, open DPs and their demands are uniquely determined by $S_D$ and these parameters (the values for $F_v$ and $x'_v$) are transferred as inputs for the feeder subproblem (F). If the last stage returns a feasible solution for (F), after merging it with $S_D$, we obtain a feasible 2FTTx solution. The advantage of calling the (F) subproblem at the beginning is that it gives us a “global view” to the problem, by incorporating the global connectivity requirements.

Each of the subproblems in this procedure is solved as a branch-and-cut, reusing the cuts and feasible solutions from the previous iterations. Since these B&C algorithms are called as heuristic procedures, we do not search for the optimal solution, but we stop the execution of these frameworks as soon as two feasible solutions are found.

Lagrangian heuristic for the (FC) + (FP) decomposition

Pseudo-code of this heuristic is given in Algorithm 2. This heuristic first solves the fixed charge subproblem (FC), including all connectivity constraints (16)–(18), and inequalities (37)–(43). That way, the topology of the network is determined, and it only remains to make capacity and routing decisions. To do so, we create a subgraph $\tilde{G}$ of $G$, induced by the given topology, and resolve the whole aggregated MIP on it. This aggregated MIP also contains constraints (16)–(18) and (37)–(39), but solving it is usually much faster than solving the original aggregated MIP, due to the fixing of variables.

Computational results

Branch-and-cut (B&C) algorithms

Each of the problems, the aggregated MIP with connectivity constraints (16)–(18), the distribution subproblem (D), the feeder subproblem (F), and the fixed-charge subproblem (FC), is solved using branch-and-cut algorithms. In this section, we explain the main ingredients of these algorithms, which are implemented in C++ using Cplex 12.4 callable library.

Separation of connectivity cuts

Connectivity constraints are separated using maximum flows, as explained in the proof of Lemma 1. The maximum flow is calculated using the push-relabel procedure (see, e.g., Cherkassky and Goldberg 1997). To speed-up the separation, we exploit the idea of backward cuts to detect more diverse cuts, further away from the artificial root node. The idea, applied to constraints (16), for example, is as follows: First, the arcs of the original graph are reversed. Then, the maximum flow from a customer towards the artificial root node is calculated. If violated, the arcs of the associated minimum cut are reversed and the corresponding connectivity cut is added to the model. We enforce generation of sparse cuts by adding an $\varepsilon$ value to each edge, and use nested cuts to generate more cuts in less iterations (see, e.g., Ljubić et al. 2006). At each call of the separation callback, we generate a new random ordering of the customers to avoid separating cuts corresponding to the same (already satisfied) customers over and over. The cut separation is not executed for another customer during a run if the number of already generated cuts exceeds $100$. The cut separator is called at the root node of the branch-and-bound tree and at every further node with quadratic index. The cut separator is also used to check feasibility of integral solutions in the course of which lazy constraints are generated.

Cut pools and warm start

Since branch-and-cut algorithms are called in each iteration of the Lagrangian decomposition approach, our implementation of the (F), (D), and (FC) models uses cut pools to store previously detected violated cuts and reuse them in each new iteration in a warm-start fashion. This is possible because from iteration to iteration only the objective function changes (due to the new dual multipliers), and the polytopes associated with feasible solutions remain the same. Hence, connectivity cuts (16)–(18) detected in earlier iterations can be reused without the computational effort of (re-)computing maximum flows.

Similarly, the best solution among the ones found in previous iterations is set as the initial feasible solution at the beginning of each branch-and-cut execution, which substantially reduces the time required to solve the subproblems.

Primal heuristics

Cplex’s default heuristics were turned on, and for the branch-and-cut runs called from within the Lagrangian heuristics Cplex’s parameters were set to emphasize finding feasible solutions.

In addition, we enhance the search for upper bounds of the (FC) model by our own upper bounding procedure. This procedure is a LP-rounding heuristics based on the following approach: (i) First, a set of terminals is determined, depending on the fractional values of $x$ and $z$ variables; (ii) Then, a Steiner tree is built to connect those terminals; and (iii) finally, the remaining variables are calculated using an auxiliary MIP in which the Steiner tree edges are fixed to one $(w_e :=1)$, and the remaining edges are fixed to zero $(w_e :=0)$.

To determine the subset of terminals, we apply an LP-rounding technique: Terminals are customers plus all nodes $v \in V_\mathrm{{D}} \cup V_\text {CO}$ whose corresponding LP values $x_v$ and $z_v$ are greater or equal to a given threshold $\pi$. In the default implementation, $\pi$ is set to $1/2$.

For calculating the Steiner tree on a given set of terminals, we apply the distance network heuristic (see, e.g., Mehlhorn 1988): First, we build a distance network, which is a weighted complete graph spanning the terminals. The weights of the edges in the distance network are the lengths of shortest paths between the corresponding terminals in the original graph $G$ using the values of the $w_e$ variables as edge lengths. Then, we compute a minimum spanning tree (MST) in the distance network and map its edges back to the paths in the original network. The resulting graph spans all terminals, but still may contain cycles. To obtain a Steiner tree, we then compute a MST in this graph and finally prune non-terminal leaves from this tree.

MIP initialization

All valid inequalities mentioned for models (F), (D), (FC), and the aggregated MIP are added at the very beginning to the MIP, except the connectivity constraints (16)–(18), which are separated during the execution of the branch-and-cut algorithms. To strengthen the (initial) linear relaxations and speed-up the cutting plane phase of the algorithm, we add some further simple but effective inequalities to the initial formulations.

The models (D) and the aggregated MIP models are additionally initialized with:

$$\begin{aligned} \sum _{(i,j) \in A, i \ne k} w^g_{ij} + x_j&\ge w^g_{jk},\quad \text {for all } (j,k) \in A, \quad j \in V_\mathrm{{D}}~, \end{aligned}$$

(44)

$$\begin{aligned} \sum _{(i,j) \in A, i \ne k} w^g_{ij}&\ge w^g_{jk},\quad \text {for all } (j,k) \in A, \quad j \not \in V_\mathrm{{D}},\quad \text {and} \end{aligned}$$

(45)

$$\begin{aligned} \sum _{(i,j) \in \delta ^-(j)} w^g_{ij}&\ge 1,\quad \quad \,\, \text {for all } j \in V_\mathrm{{C}}. \end{aligned}$$

(46)

The models (F), (FC) and the aggregated MIP models are additionally initialized with:

$$\begin{aligned} \sum _{(i,j) \in A, i \ne k} w^f_{ij} + z_j&\ge w^f_{jk},\quad \text {for all } (j,k) \in A, \, j \in V_\text {CO}~, \end{aligned}$$

(47)

$$\begin{aligned} \sum _{(i,j) \in A, i \ne k} w^f_{ij}&\ge w^f_{jk},\quad \text {for all } (j,k) \in A, \, j \not \in V_\text {CO}~, \end{aligned}$$

(48)

$$\begin{aligned} \sum _{(i,j) \in \delta ^-(j)} w^f_{ij}&\ge x_j,\quad \!\quad \text {for all } j \in V_\mathrm{{D}}~\text {, and} \end{aligned}$$

(49)

$$\begin{aligned} \sum _{(i,j) \in \delta ^-(j)} w^f_{ij}&\ge 1,\quad \,\,\quad \text {for all } j \in V_\mathrm{{C}}~. \end{aligned}$$

(50)

Inequality (44) states that for each distribution point that has a selected outgoing arc $(j,k)$, there should be an incoming $g$-arc from a node not $k$ or it should be selected as a distribution point. Inequality (45) states that each node that is not a distribution point and has a selected outgoing arc into $g$ also needs to have an incoming arc. Inequality (46) states that every customer needs to have an incoming arc selected which is necessary to satisfy his demand.

Inequalities (47)–(49) state similar things as the inequalities before, but enforce the constraints also on the feeder network. We also enforce that each customer has an incoming feeder arc via inequality (50), which was not required in the original model and has no effect on the feasible integer edge vectors $w$, but strengthens the LP relaxation after the decomposition.

Implementation details

The branch-and-cut algorithms were implemented in C++ using the Cplex 12.4 callable library. All experiments were performed on AMD Phenom II X6 machines with 8 GB RAM and 6 CPU cores running at 3.2 GHz. Our cut separators are thread-safe and we run CPLEX in a multi-threaded way to exploit the parallel computational power of modern processors. For the separation of constraints (16)–(18), we use the max-flow implementation by Goldberg (2012). The ConicBundle algorithm (available at Helmberg 2012) of Helmberg and Kiwiel (2002) is used to solve the convex optimization problem of finding the optimal Lagrangian dual multipliers. In both decomposition approaches, we use two independent bundles of subgradients to describe the dual functions corresponding either to the two problems (F) and (D) in the (F) + (D)-Decomposition or to the two problems (FC) and (FP) in the (FC) + (FP)-Decomposition. To keep the number of evaluations of the mixed-integer subproblems small, we use a large maximum bundle size of 100 for both dual functions in both decomposition approaches.

Benchmark instances

We consider a set of nine benchmark instances of different sizes originating from the German research project FTTx-Plan (2013). These instances correspond to typical regional fiber deployment planning problems—both FTTH and FTTB—in (mostly urban) regions that can be covered by 1 to 15 central offices. Some of the benchmark instances correspond to real-world planning problems provided by industry partners. For the other instances, the underlying networks are generated from publicly available street network information by considering realistic scenarios of potential customers, distribution points, and central offices in a region of typical size and creating potential connections along one or both sides of street segments depending on the street type, from the customer locations to the closest streets, and appropriate interconnection points and edges at crossings and joins. Figure 4 shows the networks of instances “a” and “c” embedded in Google Maps. Costs and capacities are obtained by mapping the very complex real-world network component costs, parameters, and installation costs of a typical GPON system to the simpler cost and capacity model used in our optimization model.

Fig. 4

Two input instances: squares, triangles and circles represent potential COs, potential DPs and customers, respectively. Maps courtesy of Google Maps

Table 1 provides the most important parameters of these benchmark instances. The number of customer locations to be served ranges from 36 in the smallest instance to 3,862 in the largest one. The average fiber demand per customer location ranges from 2.0 to 13.5. The total number of edges, which correspond to the trails or street segments that may be used by the network, ranges from approximately 800 in the smallest instance to approximately 12,500 in the largest one.

Table 1 Overview of basic instance properties

The benchmark instances used in our experiments correspond to so-called greenfield planning problems, where edges, DPs, and COs (mostly) need to be build from scratch. Accordingly, the fixed charge costs associated with the installation of an edge, of a DPs, or of a COs also contain the cost for trenching and installing ducts, cabinets, or underground closures. Table 1 also shows the average values of these fixed setup costs in our instances. The fixed setup costs for COs and DPs depend on the device type (underground closure vs. street cabinet DP, for example) and on its location and vary only moderately among the different potential CO and DP locations. The fixed setup cost of the edges, on the other hand, also depends linearly on the length of the edges and varies a lot within each instance, ranging from $0$ for edges connecting co-located nodes to $45$ times the average (instance “d”) or 20 % of the average setup cost a CO (instances “h”, “i”). In general, the average fixed charge setup cost of an edge is of the same order as the average setup cost of a DP.

The fiber installation costs depend linearly on the length of the edges in all instances. In the distribution network, a fiber installation typically uses a larger number of smaller cables and ducts with a higher fraction of dead (i.e., unused) fibers than this is the case in the feeder network. To account for this fact, the fiber installation costs in the distribution network are larger than those in the feeder network in our instances. For the smaller instances “a”, “b”, and “d”, distribution fibers cost approximately 5.3 times as much as feeder fibers per kilometer. In the other instances, they cost approximately 1.3 times as much. The fixed charge setup costs of the edges, however, highly dominate the costs for installing fibers along the edges in our greenfield planning problems. The fixed setup cost of an edge is approximately 3,000 times the cost of a single feeder fiber installed on this edge.

In all instances, we consider the same five splitter types with splitting ratios of 2, 4, 8, 16, and 32, and cost $161$, $272$, $352$, $427$, and $890$ per device, respectively. Thus, the cost of a 1:32 splitter ranges between $450$ and 4,000 times the average feeder fiber cost and between 20 and 60 % of the average DP setup cost.

In the solutions found by our algorithms, the total fixed charge setup costs for the edges, DPs, and COs clearly dominate the total flow-dependent cost for installing feeder and distribution fibers and splitters. The ratio between fixed charge costs to flow-dependent costs ranges from approximately 18:1 in instances “e” and “f” to 150:1 in instance “b”. More details on the considered technical and managerial aspects and the methodology for the generation of the original benchmark instances can be found in Martens et al. (2009, 2010), Orlowski et al. (2011).

Computations

Table 2 provides a comparison of the two decomposition approaches against the two variants of the aggregated model, one that is implemented as a branch-and-cut approach with cuts (16)–(18) (denoted by “Aggr. MIP + Cuts”) and one that is a compact aggregated MIP formulation (denoted by “Aggr. MIP”). A time limit of 2 h has been imposed on all four approaches. However, the Lagrangian decomposition approaches typically converged much faster. The column “Best UB” shows the objective value of the best solution found among all four approaches. For the two decomposition approaches (denoted by “(F) + (D) Decomp.” and “(FC) + (FP) Decomp.”, resp.), we report the final gap obtained at the end of the last iteration ($gap [\%]$), the gap of the final lower bound with respect to the global upper bound reported as “Best UB” ($gap _{ UB }[\%]$), the total number of Lagrangian iterations (#It), the total number of subproblem evaluations within the bundle method (#Evals), and the total running time [(t (s)]. Asterisk next to the running time denotes that the approach did not converge within 2 h, and the reported values are obtained in the last iteration within this time limit. For the two variants of the aggregated model, instead of the number of iterations, we report the total number of branch-and-bound nodes explored within the given time limit (#Nodes). For comparison, we also report in the column $gap _{ L }$ the relative gap obtained with the “Aggr. MIP + Cuts”-approach within the time required by “(FC) + (FP) Decomp.” to terminate and in column $t _{ L }$ the time needed by “Aggr. MIP + Cuts” to reach the same gap as “(FC) + (FP) Decomp.” at termination.

Table 2 Comparison of the two decomposition approaches, the branch-and-cut for the aggregated model and the compact aggregated model

Comparing the results provided in Table 2, we find that none of the two aggregated MIP approaches completed within 2 h. For instance “h”, the aggregated MIP approach without cuts even failed exceeding the available memory. Furthermore, we observe that the aggregated MIP approach without cuts exhibits the worst performance. For three out of nine instances, no feasible solution is found within 2 h, and for three out of remaining six, the upper bounds were above 30 %. We find that in these cases, the gaps are mainly caused by the poor quality of the bounds produced by this approach. For all instances, the number of explored branch-and-bound nodes is at least a six-figure number (with the exception of the instance “h” exceeding the memory limit).

The addition of connectivity cuts clearly improves the performance of the aggregated MIP model: The number of explored branch-and-bound nodes reduces by one to two orders of magnitude, and both the gaps and the solutions obtained after 2 h are significantly improved. However, for the large instances “e”, “f”, and “i” with more than 5,000 edges, no feasible solutions are found using the approach “Aggr. MIP + Cuts”.

In contrast to the aggregated MIP approaches, both decomposition approaches terminate much earlier with strong lower and upper bounds. The overall gaps remain below 4 % in all cases. Comparing the running times of the two decomposition approaches, we observe that (FC) + (FP) performs slightly better. Its average (median) running time is 2,369.89 (1,779) s, compared to an average (median) running time of 3,380.33 (2,365) s for (F) + (D). The quality of the solutions obtained with the two approaches is similar.

For the smaller instances, where the “Aggr. MIP + Cuts” approach was able to find feasible solutions, the final gaps obtained with this approach are slightly smaller than the ones obtained by the decomposition approaches. In these cases, the aggregated approach benefits from solving a single “global” model of the problem, which permits to fully exploit all optimization potentials via branching, while both decomposition approaches operate on a pairs of two independent submodels that are coupled only rather loosely via Lagrangian multipliers. However, we emphasize that the main purpose of the proposed Lagrangian decomposition approaches is to compute strong valid lower and upper bounds for large problem instances. This means that embedding these decomposition approaches into a (coordinated) branch-and-bound framework would further improve the obtained bounds and solutions.

To take a closer look at the performance of the proposed approaches, Figs. 5, 6, and 7 show the progress of the lower and the upper bounds for instances “d”, “e” and“f”, respectively. We observe that both decomposition approaches already reach very strong lower and upper bounds within only several minutes. In the remaining time, there is only a little progress in these values until the ConicBundle method converges (in which case the Lagrangian multipliers remain unchanged and the algorithm terminates). The two aggregated MIP models, on the other hand, improve the bounds constantly but very slowly as more branch-and-cut nodes are explored. Also, we observe that there is a significant improvement in the quality of both lower and upper bounds when adding connectivity constraints. If “Aggr. MIP + Cuts” happens to find feasible solutions, it finds them relatively early in the exploration in the branch-and-bound tree. For the aggregated MIP approach without cuts, on the other hand, good solutions are found either relatively late in the branch-and-cut process, or are not found at all.

Fig. 5

Progress of lower and upper bounds for the instance “d”: two aggregated MIP approaches (left), and two decomposition approaches (right)

Fig. 6

Progress of lower and upper bounds of four approaches on the instance “e”

Fig. 7

Progress of lower and upper bounds of four approaches on the instance “f”

When analyzing the performance of the (F) + (D) decomposition, we came to the conclusion that its convergence and the overall performance strongly depend on the initial values of Lagrangian multipliers. This can be seen from Fig. 8, which shows the progress of lower and upper bounds for the instance “a” with three different initializations of Lagrangian multipliers $\alpha _e$: (a) the installation costs of the edges are fully charged to feeder subproblem ($\alpha _e = -c_e$, $e \in E$), (b) the installation costs of the edges are fully charged to the distribution subproblem ($\alpha _e = 0$, $e \in E$), and (c) half of the installation cost of the edges is charged to both the feeder and to the distribution subproblem ($\alpha _e = -c_e/2$, $e \in E$). All other Lagrangian multipliers are initialized to zero. The presented results indicate that a “wrong” initialization of the Lagrangian multipliers can drastically slow down the overall performance.

Fig. 8

Comparison of subproblem evaluations for different settings of Lagrangian multipliers for the (F) + (D) decomposition in instance “a”

The success of the (FC) + (FP) decomposition over the (F) + (D) decomposition can be explained by the global connectivity constraints added to the fixed charge subproblem. This can be seen from Fig. 9, where we show the progress of lower and upper bounds of the (FC) + (FP) decomposition with and without adding global connectivity constraints to the fixed charge subproblem.

Fig. 9

Comparison of the (FC) + (FP) decomposition with and without global cuts in instance “a”

The results indicate that the global cuts are not only crucial for obtaining high quality lower bounds, but also for obtaining feasible solutions. When global cuts are turned off, no upper bound was found within 800 s, whereas a high quality solution is obtained in less than 100 s, otherwise. Similar behaviors to the ones reported in Figs. 8 and 9 were also observed for the remaining instances.

Recall at this point that all benchmark instances considered in this study stem from greenfield planning problems, where the setup costs of the edges include trenching costs and, thus, constitute the dominant share of the overall network cost. The impact of the global connectivity constraints may be smaller for instances stemming from planning problems where (mostly) existing edges can be used without or with only very small setup costs. Thus, the overall efficiency of the (FC) + (FP) decomposition approach observed in our experiments for greenfield planning instances may deteriorate for instances where the fixed setup cost incurred by trenching, placing closures and cabinets, opening central offices, and performing the setup activities no longer dominate the flow-dependent hardware costs for fibers and splitters in the networks.

Conclusions

In this paper, we have proposed a new combinatorial optimization problem that models a more detailed deployment of passive optical networks. To solve the problem, four mixed-integer-programming approaches were proposed: two of them consider a MIP model and solve it either as a compact MIP, or by a branch-and-cut algorithm (by adding additional valid inequalities to model connectivity). The remaining two approaches are Lagrangian decompositions whose subproblems are still NP-hard to solve, but can be efficiently tackled by branch-and-cut approaches. Our computational study has shown that the decomposition approaches outperform the aggregated MIP approaches, both with respect to the running time, and with respect to the quality of the obtained lower and upper bounds. On the other hand, design- and implementation-effort for the proposed Lagrangian decomposition approaches is much higher than for the branch-and-cut approach. Therefore, we may conclude that for a practitioner, if the running time is an issue, it pays off to develop a Lagrangian-based approach for solving 2FTTx instances; otherwise, it may be sufficient to run the (much simpler to implement) branch-and-cut approach.

Among the two decomposition approaches, a slight preference is given to the one that decomposes the problem according to its cost structure, into the fixed charge and variable cost subproblems. The reason for this is the “global view” of this approach, which is ensured by global connectivity constraints added into the fixed charge subproblem. These constraints “guide” the topology of the network throughout Lagrangian iterations. Both decomposition approaches are capable of solving realistic instances (with almost 5,000 nodes and 12,500 edges) with final gaps of only a few percents. The obtained results indicate that these decomposition approaches could be even further improved by embedding them into a branch-and-bound framework. Since the problem is new, researchers working on network design might find it interesting to consider other aspects of solving the 2-FTTx, like Benders decomposition, column generation, or to study heuristic approaches or approximation algorithms.