Revisiting Non-Parametric Maximum Likelihood Estimation of Current Status Data with Competing Risks

Abstract

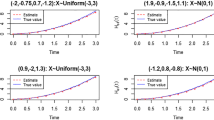
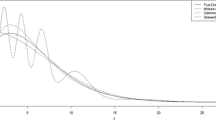
Re-parametrization is often done to make a constrained optimization problem an unconstrained one. This paper focuses on the non-parametric maximum likelihood estimation of the sub-distribution functions for current status data with competing risks. Our main aim is to propose a method using re-parametrization, which is simpler and easier to handle with compared to the constrained maximization methods discussed in Jewell and Kalbfleisch (Biostatistics. 5, 291–306, 2004) and Maathuis (2006), when both the monitoring times and the number of individuals observed at these times are fixed. Then the Expectation-Maximization (EM) algorithm is used for estimating the unknown parameters. We have also established some asymptotic results of these maximum likelihood estimators. Finite sample properties of these estimators are investigated through an extensive simulation study. Some generalizations have been discussed.

Appendix

Proof. of Theorem 1

Let us first note the following properties:

P1 : The true value of the parameter $\underset {\sim }{\lambda }$, denoted by $\underset {\sim }{\lambda _{0}}$, lies in an open set. In the present framework, we have $0 < \underset {\sim }{\lambda } < 1$ in the sense that 0 ≤ λ_ji ≤ 1, for all j, i, with some restrictions. Note that $\underset {\sim }{\lambda }= 0$ means λ_ji = 0, for all j, i, which is not of interest. Similarly$, \underset {\sim }{\lambda }= 1$ meaning λ_ji = 1, for all j, i, which is also of no interest.

P2 : Let $\underset {\sim }{\lambda }^{\prime }$ and $\underset {\sim }{\lambda }^{\prime \prime }$ be two values of the parameter vector $\underset {\sim }{\lambda }$ with $\underset {\sim }{\lambda }^{\prime } \neq \underset {\sim }{\lambda }^{\prime \prime }$. Then, there is at least one component of these two vectors which are not equal, say $, \lambda _{ji}^{\prime } \neq \lambda _{ji}^{\prime \prime }$, for some i = 1,..,k and j = 1,..,m. Also, the densities $p^{i} (\delta ^{(i)} \mid \underset {\sim }{\lambda })$’s are functions of $\lambda _{ji^{\prime }}$, for j = 1,2,..,m and i^′≤, for i = 1,...,k. Hence $,~p^{i^{\prime }} (\delta ^{(i^{\prime })} \mid \underset {\sim }{\lambda }^{\prime }) \neq p^{i^{\prime }} (\delta ^{(i^{\prime })} \mid \underset {\sim }{\lambda }^{\prime \prime })$, for i^′≥ i, and the likelihood $L(\underset {\sim }{\lambda })$, being the product of these densities $, L(\underset {\sim }{\lambda }^{\prime }) \neq L(\underset {\sim }{\lambda }^{\prime \prime })$.

P3 : For each i = 1,..,k, $E_{i,\underset {\sim }{\lambda }} \left [ \frac {\partial }{\partial \underset {\sim }{\lambda }} \log \hspace {4 pt} p^{i} (\delta ^{(i)} \mid \underset {\sim }{\lambda }) \right ] = 0$, where $E_{i,\underset {\sim }{\lambda }} \left [ \cdot \right ]$ is the expectation with respect to the density $p^{i} (\delta ^{(i)} \mid \underset {\sim }{\lambda })$. Again, differentiating with respect to $\underset {\sim }{\lambda }$, we have $E_{i,\underset {\sim }{\lambda }}\left [ \left (\frac {\partial }{\partial \underset {\sim }{\lambda }} \log \hspace {4 pt} p^{i} (\delta ^{(i)} \mid \underset {\sim }{\lambda })\right )^2 \right ] = E_{i,\underset {\sim }{\lambda }} \left [ - \frac {\partial ^2}{\partial \underset {\sim }{\lambda } \partial \underset {\sim }{\lambda }^{\text {T}}} \log \hspace {4 pt}p^{i} (\delta ^{(i)} \mid \underset {\sim }{\lambda }) \right ]$$= \mathscr{I}_i(\underset {\sim }{\lambda })$, say, which is assumed to be non-negative definite.

P4 : The density function $p^{i} (\delta ^{(i)} \mid \underset {\sim }{\lambda })$ is a polynomial in the λ_ji’s. Therefore, it is continuous in each λ_ji and admits all third order derivatives. Also, since each λ_ji is bounded above by 1, it can be shown that these third order derivatives are bounded by functions with finite expectations in a neighbourhood of the true value $\underset {\sim }{\lambda _{0}}$ of $\underset {\sim }{\lambda }$.

Let us consider a sphere Q_a with center at the true value $\underset {\sim }{\lambda _{0}}$ and radius a. We will show that, for sufficiently small value of a, log $L_I(\underset {\sim }{\lambda }) <$ log $L_I(\underset {\sim }{\lambda _{0}})$ with probability tending to 1 as n →∞ for all $\underset {\sim }{\lambda }$ on the surface of Q_a. So $, L_I(\underset {\sim }{\lambda })$ has a local maximum in the interior of Q_a and, hence, the likelihood equations have a solution within Q_a. Note that, from (4.2), we have log $L_I(\underset {\sim }{\lambda }) = {\sum }_{i = 1}^k {\sum }_{l = 1}^{n_i} p^i (\delta ^{(i)}_l \mid \underset {\sim }{\lambda })$, so that

$$\begin{array}{@{}rcl@{}} &&{}\frac{1}{n} \log L_I(\underset{\sim}{\lambda}) - \frac{1}{n}\log L_I(\underset{\sim}{\lambda_{0}})\\ &&\!\!\!\!~~= \sum\limits_{i = 1}^{k} \frac{n_{i}}{n} \times \frac{1}{n_{i}} \sum\limits_{l = 1}^{n_{i}} \left[ \log\hspace{4 pt} p^{i} (\delta^{(i)}_{l} \mid \underset{\sim}{\lambda}) - \log\hspace{4 pt} p^{i} (\delta^{(i)}_{l} \mid \underset{\sim}{\lambda_{0}}) \right]. \end{array} $$

(8.1)

Then, following the proof given in Lehmann and Casella (1998) and using the properties P1-P4, it can be proved that the maximum of (8.1), over all $\underset {\sim }{\lambda }$ on the surface of Q_a, is less than zero. This completes the proof of (i). Using Taylor’s series expansion on the likelihood equation, we have

$$\begin{array}{@{}rcl@{}} 0 \!\!\!\!&=&\!\!\!\! \frac{1}{\sqrt{n}} \sum\limits_{i = 1}^k \sum\limits_{l = 1}^{n_i} \frac{\partial}{\partial \underset{\sim}{\lambda}} \log \hspace{4 pt} p^i(\delta_l^{(i)} \mid \underset{\sim}{\lambda}) \mid_{\underset{\sim}{\lambda}= \hat{\underset{\sim}{\lambda}}}\\ \!\!\!\!&=&\!\!\!\! \sum\limits_{i = 1}^k \sqrt{\frac{n_i}{n}} \times \frac{1}{\sqrt{n_i}} \sum\limits_{l = 1}^{n_i} \frac{\partial}{\partial \underset{\sim}{\lambda}} \log\hspace{4 pt} p^i(\delta_l^{(i)} \mid \underset{\sim}{\lambda}) \mid_{\underset{\sim}{\lambda}= \underset{\sim}{\lambda_{0}}}\\ &&\!\!\!\!+\sum\limits_{i = 1}^{k} \frac{n_{i}}{n} \!\times\! \frac{1}{n_{i}} \sum\limits_{l = 1}^{n_{i}} \frac{\partial^{2}}{\partial \underset{\sim}{\lambda} \partial \underset{\sim}{\lambda}^{T}} \log \hspace{4 pt} p^{i}(\delta_{l}^{(i)} \mid \underset{\sim}{\lambda}) \mid_{\underset{\sim}{\lambda}= \underset{\sim}{\lambda_{0}}} \times \sqrt{n}(\hat{\underset{\sim}{\lambda}} - \underset{\sim}{\lambda_{0}}) + o_{p}(1).{\kern25pt} \end{array} $$

(8.2)

For a particular i, by weak law of large numbers, we have

$$\begin{array}{@{}rcl@{}} \frac{1}{n_i} {\sum}_{l = 1}^{n_i} \frac{\partial^2}{\partial \underset{\sim}{\lambda} \partial \underset{\sim}{\lambda}^T} \log {\kern4pt} p^{i}(\delta_l^{(i)} | \underset{\sim}{\lambda}){} &&|_{\underset{\sim}{\lambda}= \underset{\sim}{\lambda_{0}}} \xrightarrow{P} E\left[ \frac{\partial^2}{\partial \underset{\sim}{\lambda} \partial \underset{\sim}{\lambda}^T} \log {\kern4pt} p^i(\delta_l^{(i)} | \underset{\sim}{\lambda}) |_{\underset{\sim}{\lambda}= \underset{\sim}{\lambda_{0}}} \right]\\ &&{\kern15pt}= - \mathscr{I}_i(\underset{\sim}{\lambda_{0}}). \end{array} $$

Also, using Central Limit Theorem, we have $\frac {1}{\sqrt {n_i}} {\sum }_{l = 1}^{n_i} \frac {\partial }{\partial \underset {\sim }{\lambda }} \log {\kern 4pt} p^i(\delta _l^{(i)} | \underset {\sim }{\lambda }) | _{\underset {\sim }{\lambda }= \underset {\sim }{\lambda _{0}}} \xrightarrow {d} N(0,\mathscr{I}_i(\underset {\sim }{\lambda _{0}}))$ and $-\frac {1}{n} \frac {\partial ^2}{\partial \underset {\sim }{\lambda } \partial \underset {\sim }{\lambda }^T} \log {\kern 4pt} L_I(\underset {\sim }{\lambda })= - {\sum }_{i = 1}^{k} \frac {n_i}{n} \times \frac {1}{n_i} {\sum }_{l = 1}^{n_i} \frac {\partial ^2}{\partial \underset {\sim }{\lambda } \partial \underset {\sim }{\lambda }^T} \log {\kern 4pt} p^{i}(\delta _l^{(i)} | \underset {\sim }{\lambda })$$\xrightarrow {p} {\sum }_{i = 1}^{k} w_i \mathscr{I}_i(\underset {\sim }{\lambda })= \mathscr{I}(\underset {\sim }{\lambda }),$ say. Using these results and Slutsky’s theorem, we have from (8.2), $\sqrt {n}(\hat {\underset {\sim }{\lambda }} - \underset {\sim }{\lambda _{0}}) \xrightarrow {d} N(0,\mathscr{I}^{-1}(\underset {\sim }{\lambda _{0}}))$. This completes the proof of (ii). Note that, since $\hat {\underset {\sim }{\lambda }}$ is a consistent estimate, using the weak law of large numbers, as before$, -\frac {1}{n} \frac {\partial ^2}{ \partial \underset {\sim }{\lambda } \partial \underset {\sim }{\lambda }^T} \log \hspace {4 pt} L_I(\underset {\sim }{\lambda })$ evaluated at $\underset {\sim }{\lambda }= \hat {\underset {\sim }{\lambda }}$ can be taken as a consistent estimate of $\mathscr{I}(\underset {\sim }{\lambda _{0}}) ={\sum }_{i = 1}^k w_i \mathscr{I}_i(\underset {\sim }{\lambda })$.