Skip to main content

Advertisement

SpringerLink
Log in

Mechanical Analysis and Energy Cycle of Chen Chaotic System

  • General and Applied Physics
  • Published:
Brazilian Journal of Physics Aims and scope Submit manuscript

Abstract

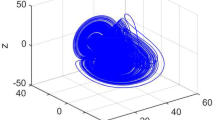
This paper formulates the Chen chaotic system to the extended Kolmogorov system, thereby investigating the physical meaning and energy cycle of Chen system. The Casimir function is introduced to analyze the system dynamics, and its time derivation is chosen to formulate energy cycle. The bound of chaotic attractor is obtained by the Casimir function and Lagrange multiplier. The Casimir function reflects the energy conversion and the distance between the orbit and the equilibria. These relationships are illustrated by numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. E. Lorenz, Deterministic nonperiodic flow. J. Atmos. Sci. 20(2), 130 (1963)

    Article  ADS  Google Scholar 

  2. D. D’Humieres, B.M. R., B.A. Humberman, A. Libchaber, Chaotic states and routes to chaos in the forced pendulum. Phys. Rev. A. 26(6), 3483 (1982)

    Article  ADS  Google Scholar 

  3. F.A. Hopf, D.L. Kaplan, H.M. Gibbs, R.L. Shoemaker, Bifurcations to chaos in optical bistability. Phys. Rev. A. 25(4), 2172 (1982)

    Article  ADS  MathSciNet  Google Scholar 

  4. H.G. Schuster, W. Just. Deterministic Chaos: An Introduction, 4th edn (WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2005)

    Book  MATH  Google Scholar 

  5. R.H. Simoyi, A. Wolf, H.L. Swinney, One-dimensional dynamics in a multicomponent chemical reaction. Phys. Rev. Lett. 49(4), 245 (1982)

    Article  ADS  MathSciNet  Google Scholar 

  6. H.L. Swinney, J.P. Gollub. Hydrodynamic Instabilities and the Transition to Turbulence (Springer, Berlin-Heidelberg-New York-Tokyo, 1981)

    Book  MATH  Google Scholar 

  7. A. Hernández-García, A. Fernández Barbero, O. Sotolongo-Costa, Non-steady wall-bounded flows of viscoelastic fluids under periodic forcing. Braz. J. Phys. 44(4), 315 (2014)

    Article  ADS  Google Scholar 

  8. R.M. May, Simple mathematical models with very complicated dynamics. Nature. 261, 459 (1976)

    Article  ADS  Google Scholar 

  9. E.D. Souza, M. Lyra, I. Gleria, Critical behavior of the delay-induced chaos transition in a nonlinear model for the immune response. Braz. J. Phys. 39, 431 (2009)

    Article  ADS  MATH  Google Scholar 

  10. G. Chen, T. Ueta, Yet another chaotic attractor. Int. Bifurcat, J., Chaos. 9(7), 1465 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  11. J. Lu, G. Chen, A new chaotic attractor coined. Int. Bifurcat, J., Chaos. 12(3), 659 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  12. G. Qi, G. Chen, M.A.V. Wyk, B.J.V. Wyk, Y. Zhang, A four-wing chaotic attractor generated from a new 3-D quadratic autonomous system. Chaos Soliton. Fract. 38(3), 705 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. J. Lu, G. Chen, X. Yu, H. Leung, Design and analysis of multiscroll chaotic attractors from saturated function series. IEEE Trans. Circuits Syst. I. 51(12), 2476 (2005)

    Article  MathSciNet  Google Scholar 

  14. G. Qi, G. Chen, S.S.Z. Du, Z. Chen, Z. Yuan, Analysis of a new chaotic system. Physica A. 352 (2), 295 (2005)

    Article  ADS  Google Scholar 

  15. Z. Wang, Y. Sun, B.J. van Wyk, G. Qi, M.A. van Wyk, A 3-D four-wing attractor and its analysis. Braz. Phys, J.,. 39, 547 (2009)

  16. A. Pasini, V. Pelino, A unified view of Kolmogorov and Lorenz systems. Phys. Lett. A. 275, 435 (2000)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. V. Pelino, F. Maimone, A. Pasini, Energy cycle for the Lorenz attractor. Chaos Soliton. Fract. 64, 67 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. A. Gluhovsky, Energy-conserving and Hamiltonian low-order models in geophysical fluid dynamics. Nonlinear Processes Geophys. 13(2), 125 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  19. E. Pavlovskaia, M. Wiercigroch, C. Grebogi, Modeling of an impact system with a drift. Phys. Rev. E. 64(2), 056224 (2001)

    Article  ADS  Google Scholar 

  20. Z. Lu, C. Jarzynski, E. Ott, Apparent topologically forbidden interchange of energy surfaces under slow variation of a Hamiltonian. Phys. Rev. E. 91(5), 052193 (2015)

    Article  MathSciNet  Google Scholar 

  21. R. Fitzpatrick, An introduction to celestial mechanics: Cambridge University Press (2012)

  22. J. Marsden, T. Ratiu. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, 2nd edn (Springer, Berlin, 2002)

    MATH  Google Scholar 

  23. V. Arnold, Kolmogorov’s hydrodynamic attractors. Proc. Soc, R., Lond. A. 434, 19 (1991)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. G. Qi, X. Liang, Mechanical analysis of Qi four-wing chaotic system. Nonlinear Dyn. 86(2), 1095 (2016)

    Article  MathSciNet  Google Scholar 

  25. C.R. Doering, J.D. Gibbon, On the shape and dimension of the Lorenz attractor. Dyn. Stab. Syst. 10(3), 255 (1995)

    MathSciNet  MATH  Google Scholar 

  26. P.J. Morrison, Thoughts on brackets and dissipation: Old and new. Journal of Physics: Conference Series. 169 (1), 012006 (2009)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Science and School of Mechanical Engineering, Tianjin Polytechnic University, Tianjin, 300387, China

    Xiyin Liang

  2. Tianjin Key Laboratory of Advanced Technology of Electrical Engineering and Energy, Tianjin Polytechnic University, Tianjin, 300387, China

    Guoyuan Qi

Authors
  1. Xiyin Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guoyuan Qi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guoyuan Qi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liang, X., Qi, G. Mechanical Analysis and Energy Cycle of Chen Chaotic System. Braz J Phys 47, 288–294 (2017). https://doi.org/10.1007/s13538-017-0495-y

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13538-017-0495-y

Keywords

Search

Navigation