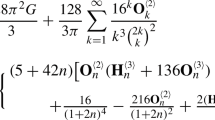Skip to main content
SpringerLink
Log in

Infinite series on quadratic skew harmonic numbers

  • Original Paper
  • Published:
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas Aims and scope Submit manuscript

Abstract

By combining hypergeometric series computations with partial fraction decompositions, we present full solutions to the evaluation problems about two classes of infinite series involving squared central binomial coefficients and quadratic skew harmonic numbers. Two further series of similar type are also examined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

Not appilicable.

References

  1. Adamchik, V.: Thirty-three representations of Catalan’s constant. https://library.wolfram.com/infocenter/Demos/109/

  2. Bailey, W.N.: Generalized Hypergeometric Series. Cambridge University Press, Cambridge (1935)

    MATH  Google Scholar 

  3. Campbell, J.M.: Ramanujan-like series for \(\frac{1}{\pi }\) involving harmonic numbers. Ramanujan J. 46(2), 373–387 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  4. Campbell, J.M.: A Wilf-Zeilberger-based solution to the Basel problem with applications. Discrete Math. Lett. 10, 21–27 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  5. Campbell, J.M., D’Aurizio, J., Sondow, J.: On the interplay among hypergeometric functions, complete elliptic integrals, and Fourier–Legendre expansions. J. Math. Anal. Appl. 479(1), 90–121 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chu, W., Campbell, J.M.: Harmonic sums from the Kummer theorem. J. Math. Anal. Appl. 501(2), Article 125179; pp. 37 (2021)

  7. Nimbran, A. S., Levrie, P., Sofo, A.: Harmonic-binomial Euler-like sums via expansions of \((\text{ arcsin }\,x)^p\). RACSAM 116(23), 23 (2022). https://doi.org/10.1007/s13398-021-01156-7

    Article  MATH  Google Scholar 

  8. Rainville, E.D.: Special Functions. The Macmillan Company, New York (1960)

    MATH  Google Scholar 

  9. Ramanujan, S.: Notebooks of Srinivasa Ramanujan, vol. 1. Tata Institute of Fundamental Research, Bombay (1957)

    MATH  Google Scholar 

  10. Wang, X.Y., Chu, W.: Further Ramanujan-like series containing harmonic numbers and squared binomial coefficients. Ramanujan J. 52(3), 641–668 (2020). https://doi.org/10.1007/s11139-019-00140-5

  11. Wang, X., Chu, W.: Series with harmonic-like numbers and squared binomial coefficients. Rocky Mt. J. Math. (2022). https://projecteuclid.org/journals/rmjm/rocky-mountain-journal-of-mathematics/DownloadAcceptedPapers/210216-Wang-2.pdf

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Zhoukou Normal University, Zhoukou, Henan, China

    Wenchang Chu

  2. Department of Mathematics and Physics, University of Salento, 73100, Lecce, Italy

    Wenchang Chu

Authors
  1. Wenchang Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenchang Chu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chu, W. Infinite series on quadratic skew harmonic numbers. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 117, 75 (2023). https://doi.org/10.1007/s13398-023-01407-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s13398-023-01407-9

Keywords

Mathematics Subject Classification

Search

Navigation