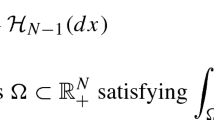Minimizer of an isoperimetric ratio on a metric on ${\mathbb {R}}^2$ with finite total area

Abstract

Let $g=(g_{ij})$ be a complete Riemmanian metric on ${\mathbb {R}}^2$ with finite total area and let $I_g$ be the infimum of the quotient of the length of any closed simple curve $\gamma$ in ${\mathbb {R}}^2$ and the sum of the reciprocal of the areas of the regions inside and outside $\gamma$ respectively with respect to the metric g. Under some mild growth conditions on g we prove the existence of a minimizer for $I_g$. As a corollary we obtain a proof for the existence of a minimizer for $I_{g(t)}$ for any $0<t<T$ when the metric $g(t)=g_{ij}(\cdot ,t)=u\delta _{ij}$ is the maximal solution of the Ricci flow equation $\partial g_{ij}/\partial t=-2R_{ij}$ on ${\mathbb {R}}^2\times (0,T)$ (Daskalopoulos and Hamilton in Commun Anal Geom 12(1):143–164, 2004) where $T>0$ is the extinction time of the solution. This existence of minimizer result is assumed and used without proof by Daskalopoulos and Hamilton (2004).

1 Introduction

Isoperimetric inequalities arises in many problems in analysis and geometry such as the study of partial differential equations and Sobolev inequality [1, 17]. In [8, 11], Gage and Hamilton studied isoperimetric inequalities arising from the curve shortening flow. In [2] Daskalopoulos and Hamilton assumed the existence of a minimizer for an isoperimetric inequality corresponding to the maximal solution of the finite mass 2-dimensional Ricci flow on ${\mathbb {R}}^2$ and studied various properties of this isoperimetric inequality. However there is no proof of the existence of this minimizer in [2] and there is also no proof of this important existence result in other papers. In [3, 4, 6], Daskalopoulos, Hamilton, Del Pino and Sesum used these properties to study the behaviour of ancient solution of Ricci flow and the extinction behavior of finite mass maximal solution of Ricci flow, which is an important tool in the classification of manifolds [14,15,16, 18].

Since the existence of such minimizer is crucial to the proof of various theorems in [2, 3, 5, 6], in this paper I will give a rigorous proof of this important existence result. In fact my existence result holds for any metrics that satisfies some structural conditions which include the maximal finite mass solution of the 2-dimensional Ricci flow as a special case.

Let $g=(g_{ij})$ be a complete Riemannian metric on ${\mathbb {R}}^2$ with finite total area $A=\int _{{\mathbb {R}}^2}\,dV_g$ satisfying

$$\begin{aligned} \lambda _1(|x|)\delta _{ij}\le g_{ij}(x)\le \lambda _2(|x|)\delta _{ij}\quad \forall |x|\ge r_0 \end{aligned}$$

(1.1)

for some constant $r_0>1$ and positive monotone decreasing functions $\lambda _1(r)$, $\lambda _2(r)$, on $[r_0,\infty )$ that satisfy

$$\begin{aligned}&\int _r^{c_0r}\sqrt{\lambda _1(\rho )}\,d\rho \ge \pi r\sqrt{\lambda _2(r)} \quad \forall r\ge r_0, \end{aligned}$$

(1.2)

$$\begin{aligned}&r\sqrt{\lambda _1(c_0r)}\ge b_1\int _r^{\infty }\rho \lambda _2(\rho ) \,d\rho \quad \forall r\ge r_0, \end{aligned}$$

(1.3)

$$\begin{aligned}&\int _r^{r^2}\sqrt{\lambda _1(\rho )}\,d\rho \ge b_2\quad \forall r\ge r_0, \end{aligned}$$

(1.4)

and

$$\begin{aligned} \lambda _1(c_0r)\ge \delta \lambda _2(r)\quad \forall r\ge r_0 \end{aligned}$$

(1.5)

for some constants $c_0>1$, $b_1>0$, $b_2>0$, $\delta >0$, where |x| is the distance of x from the origin with respect to the Euclidean metric. For any closed simple curve $\gamma$ in ${\mathbb {R}}^2$, let (cf. [2])

$$\begin{aligned} I(\gamma ) =L(\gamma )\left( \frac{1}{A_{in}(\gamma )}+\frac{1}{A_{out}(\gamma )}\right) , \end{aligned}$$

(1.6)

where $L(\gamma )$ is the length of the curve $\gamma$, $A_{in}(\gamma )$ and $A_{out}(\gamma )$ are the areas of the regions inside and outside $\gamma$ respectively, with respect to the metric g. Let

$$\begin{aligned} I=I_g=\inf _{\tiny \begin{array}{c}\gamma \end{array}}I(\gamma ) \end{aligned}$$

(1.7)

where the infimum is over all closed simple curves $\gamma$ in ${\mathbb {R}}^2$. In this paper we will prove that there exists a constant $b_0>0$ such that if $I_g<b_0$, then there exists a closed simple curve $\gamma$ satisfying $I_g=I(\gamma )$. As a corollary we obtain a proof for the existence of a minimizer for the isoperimetric ratio $I_{g(t)}$ for any $0<t<T$ when the metric $g(t)=g_{ij}(\cdot ,t)=u\delta _{ij}$ is the maximal solution of the Ricci flow [2]

$$\begin{aligned} \frac{\partial }{\partial t}g_{ij}=-2R_{ij}\quad \text{ on } {\mathbb {R}}^2\times (0,T), \end{aligned}$$

where $T>0$ is the extinction time of the solution and u is a solution of

$$\begin{aligned} u_t=\Delta \log u\quad \text{ on } {\mathbb {R}}^2\times (0,T). \end{aligned}$$

(1.8)

We will adapt and modify the techniques in [11, 12] to prove the result. Since the domain under consideration in [11, 12], is either the sphere $S^2$ ([12]) or a bounded domain, the minimizing sequences for the infimum of the isoperimetric ratios considered in those cases stay in a compact set. On the other hand since the isoperimetric ratio (1.6) is for any curve $\gamma$ in ${\mathbb {R}}^2$, the minimizing sequence of curves for the infimum of the isoperimetric ratio (1.7) may not stay in a compact subset of ${\mathbb {R}}^2$ and may not have a limit at all. The technique for compact manifold [12] is not sufficient to prove this result. New technique and ideas are used in this paper to prove the result. We will show that there exists a constant such that this is impossible when $I_g$ is less than this constant. After this we will use the curve shortening flow technique of [12] to modify the minimizing sequence of curves and show that they will converge to a minimizer of (1.7).

For any $x_0\in {\mathbb {R}}^2$ and $r>0$ let $B_r(x_0)=\{x\in {\mathbb {R}}^2:|x-x_0|<r\}$ and $B_r=B_r(0)$. The main results of the paper are as follows.

Theorem 1.1

Suppose g satisfies (1.1) for some constant $r_0>1$ where $\lambda _1(r)$, $\lambda _2(r)$, are positive monotone decreasing functions on $[r_0,\infty )$ that satisfy (1.2), (1.3), (1.4) and (1.5) for some constants $c_0>1$, $b_1>0$, $b_2>0$ and $\delta >0$. Then there exists a constant $b_0>0$ depending on $b_1$, $b_2$ and A such that the following holds:

If

$$\begin{aligned} I_g<b_0, \end{aligned}$$

(1.9)

then there exists a closed simple curve $\gamma$ in ${\mathbb {R}}^2$ such that $I_g=I(\gamma )$. Hence $I_g>0$.

Proposition 1.2

Suppose $g=(g_{ij})$ satisfies

$$\begin{aligned} \frac{C_1}{r^2(\log r)^2}\delta _{ij}\le g_{ij} \le \frac{C_2}{r^2(\log r)^2}\delta _{ij}\quad \forall r\ge r_1 \end{aligned}$$

for some constants $C_2\ge C_1>0$, $r_1>1$. Then there exist constants $c_0>1$, $\delta >0$, $b_1>0$, $b_2>0$, and $r_0\ge r_1$ such that (1.2), (1.3), (1.4) and (1.5) hold.

Corollary 1.3

Let $g_{ij}(x,t)=u(x,t)\delta _{ij}$ where u is the maximal solution of (1.8) with initial value $0\le u_0\in L^p({\mathbb {R}}^2)\cap L^1({\mathbb {R}}^2)$, $u_0\not \equiv 0$, for some $p>1$ satisfying

$$\begin{aligned} u_0(x)\le \frac{C}{|x|^2 (\log |x|)^2}\quad \forall |x|>1 \end{aligned}$$

(1.10)

given by [4, 13] where $T=(1/4\pi )\int _{{\mathbb {R}}^2}u_0\,dx$. Then for any $0<t_1<T$ there exists a constant $b_0>0$ such that the following holds:

For any $t_1\le t<T$, if $I_{g(t)}<b_0$, then there exists a closed simple curve $\gamma$ that satisfies $I_{g(t)}=I(\gamma )$.

By an argument similar to the proof of Proposition 1.2 we also have the following result.

Remark 1.4

Suppose $g=(g_{ij})$ satisfies

$$\begin{aligned} \frac{C_1}{r^2(\log r)^2(1+\log r)^2}\delta _{ij}\le g_{ij} \le \frac{C_2}{r^2(\log r)^2(1+\log r)^2}\delta _{ij}\quad \forall r\ge r_1 \end{aligned}$$

for some constants $C_2\ge C_1>0$, $r_1>1$. Then there exist constants $c_0>1$, $\delta >0$, $b_1>0$, $b_2>0$, and $r_0\ge r_1$ such that (1.2), (1.3), (1.4) and (1.5) hold. The growth condition for g here is different from that of Proposition 1.2. Hence Theorem 1.1 is more general than the minimizer result used by Daskalopoulos and Hamilton [2].

2 The proof of the main results

Proof of Proposition 1.2

Let $\lambda _i(r)=C_i(r\log r)^{-2}$, $i=1,2$,

$$\begin{aligned} c_0=2e^{\pi \sqrt{C_2/C_1}}, \end{aligned}$$

(2.1)

and $\delta =C_1/(2c_0^2C_2)$. We choose $r_2\ge r_1$ such that

$$\begin{aligned} \frac{\log r}{\log (c_0r)}\ge \frac{1}{\sqrt{2}}\quad \forall r\ge r_2. \end{aligned}$$

(2.2)

Then by (2.1) and (2.2),

$$\begin{aligned} \frac{\lambda _1(c_0r)}{\lambda _2(r)}=\frac{C_1}{c_0^2C_2} \left( \frac{\log r}{\log (c_0r)}\right) ^2\ge \frac{C_1}{2c_0^2C_2}=\delta \quad \forall r\ge r_2. \end{aligned}$$

(2.3)

We next note that

$$\begin{aligned} \lim _{r\rightarrow \infty }\left( (\log r)\log \left( \frac{\log (c_0r)}{\log r}\right) \right) =\lim _{z\rightarrow 0}\frac{\log ((\log c_0)z+1)}{z}=\log c_0. \end{aligned}$$

(2.4)

By (2.1) and (2.4) there exists $r_0\ge r_2$ such that

$$\begin{aligned} (\log r)\log \left( \frac{\log (c_0r)}{\log r}\right) >\pi \sqrt{C_2/C_1} \quad \forall r\ge r_0. \end{aligned}$$

(2.5)

By (2.3) and (2.5), we get (1.2) and (1.5). By (2.2) and a direct computation (1.3) and (1.4) holds with $b_1=\sqrt{C_1}/(\sqrt{2}c_0C_2)$, $b_2=\sqrt{C_1}\log 2$, and the proposition follows. $\square$

Proof of Corollary 1.3

By (1.10) and the results of [7] there exists a constant $C_2>0$ such that

$$\begin{aligned} u(x,t)\le \frac{C_2}{|x|^2(\log |x|)^2}\quad \forall |x|>1,0<t<T \end{aligned}$$

(2.6)

and for any $t_0\in (0,T)$ there exists a constant $r_1>1$ such that

$$\begin{aligned} u(x,t)\ge \frac{(3/2)t}{|x|^2(\log |x|)^2}\quad \forall |x|\ge r_1,0<t\le t_0. \end{aligned}$$

(2.7)

By (2.6), (2.7), Theorem 1.1 and Proposition 1.2, the corollary follows. $\square$

Henceforth we will assume that g is a metric on ${\mathbb {R}}^2$ with finite total area that satisfies (1.1), (1.2), (1.3), (1.4) and (1.5) for some constants $r_0>1$, $c_0>1$, $b_1>0$, $b_2>0$, $\delta >0$ where $\lambda _1(r)$, $\lambda _2(r)$, are positive monotone decreasing functions on $[r_0,\infty )$. Let $b_0=\min (b_1,4b_2/A)$. Suppose (1.9) holds. Let $\{\gamma _k\}_{k=1}^{\infty }$ be a sequence of closed simple curves on ${\mathbb {R}}^2$ such that

$$\begin{aligned} I(\gamma _k)\rightarrow I\quad \text{ as } k\rightarrow \infty \quad \text{ and } \quad I(\gamma _k)<b_0\quad \forall k\in {\mathbb {Z}}^+. \end{aligned}$$

(2.8)

We will show that the sequence $\{\gamma _k\}_{k=1}^{\infty }$ is contained in some compact set of ${\mathbb {R}}^2$. Let $\Omega _k$ be the region inside $\gamma _k$ and $r_k=\min _{x\in \gamma _k} |x|$. Let $L_e(\gamma _k)$ be the length of $\gamma _k$ and $|\Omega _k|$ be the area of $\Omega _k$ with respect to the Euclidean metric. We choose $r_0'>r_0$ such that

$$\begin{aligned} \text{ Vol }_g\left( {\mathbb {R}}^2{\setminus } B_{r_0'}\right) \le \frac{A}{4}\quad \forall k\in {\mathbb {Z}}^+. \end{aligned}$$

(2.9)

Lemma 2.1

The sequence $r_k$ is uniformly bounded.

Proof

Suppose the lemma is not true. Then there exists a subsequence of $r_k$ which we may assume without loss of generality to be the sequence itself such that

$$\begin{aligned} r_k>r_0'\quad \forall k\in {\mathbb {Z}}^+ \end{aligned}$$

(2.10)

and $r_k\rightarrow \infty$ as $k\rightarrow \infty$. Let $\widetilde{\gamma }_k=\partial B_{r_k}$. We choose a point $x_k\in \gamma _k\cap \partial B_{r_k}$ and let $\gamma _k:[0,2\pi ]\rightarrow {\mathbb {R}}^2$ be a parametrization of the curve $\gamma _k$ such that $x_k=\gamma _k(0)=\gamma _k(2\pi )$. Since for any $k\in {\mathbb {Z}}^+$ either $0\in \Omega _k$ or $0\in {\mathbb {R}}^2{\setminus } \Omega _k$ holds, thus either

$$\begin{aligned} 0\in \Omega _k\quad \text{ for } \text{ infinitely } \text{ many } \text{ k } \end{aligned}$$

(2.11)

or

$$\begin{aligned} 0\in {\mathbb {R}}^2{\setminus }\Omega _k\quad \text{ for } \text{ infinitely } \text{ many } \text{ k } \end{aligned}$$

(2.12)

holds. We need the following result for the proof of the lemma.

Claim 1

There exists only finitely many k such that $\gamma _k\cap ({\mathbb {R}}^2{\setminus }\overline{B}_{c_0r_k})\ne \emptyset$.

Proof of Claim 1

Suppose claim 1 is false. Then there exists infinitely many k such that $\gamma _k\cap ({\mathbb {R}}^2{\setminus }\overline{B}_{c_0r_k})\ne \emptyset$. Without loss of generality we may assume that

$$\begin{aligned} \gamma _k\cap \left( {\mathbb {R}}^2{\setminus }\overline{B}_{c_0r_k}\right) \ne \emptyset \quad \forall k\in {\mathbb {Z}}^+. \end{aligned}$$

(2.13)

By (2.13) there exists $\phi _0\in (0,2\pi )$ such that

$$\begin{aligned} |\gamma _k(\phi _0)|>c_0r_k. \end{aligned}$$

Hence there exists $0<\phi _1<\phi _0<\phi _2<2\pi$ such that

$$\begin{aligned} \gamma _k(\phi _1)=\gamma _k(\phi _2)=c_0r_k \end{aligned}$$

and

$$\begin{aligned} r_k\le |\gamma _k(\phi )|\le c_0r_k\quad \forall \phi \in (0,\phi _1) \cup (\phi _2,2\pi ). \end{aligned}$$

Then by (1.1),

$$\begin{aligned} L(\gamma _k)=&\int _0^{2\pi }\left( g_{ij}\overset{.}{\gamma }_k^i \overset{.}{\gamma }_k^j\right) ^{\frac{1}{2}}\,d\phi \nonumber \\ \ge&\left( \int _0^{\phi _1}+\int _{\phi _2}^{2\pi }\right) \left( g_{ij}\overset{.}{\gamma }_k^i\overset{.}{\gamma }_k^j\right) ^{\frac{1}{2}} \,d\phi \nonumber \\ \ge&\left( \int _0^{\phi _1}+\int _{\phi _2}^{2\pi }\right) \sqrt{\lambda _1(r)}\sqrt{\biggl (\frac{dr}{d\phi }\biggr )^2 +r^2\biggl (\frac{d\theta }{d\phi }\biggr )^2}\,d\phi \nonumber \\ \ge&2\int _{r_k}^{c_0r_k}\sqrt{\lambda _1(r)}\,dr \end{aligned}$$

(2.14)

and

$$\begin{aligned} 2\pi r_k\sqrt{\lambda _1(r_k)} \le L(\widetilde{\gamma }_k)=\int _0^{2\pi } \left( g_{ij}\overset{.}{\widetilde{\gamma }_k^i}\overset{.}{\widetilde{\gamma }_k^j}\right) ^{\frac{1}{2}} \,d\phi \le 2\pi r_k\sqrt{\lambda _2(r_k)}. \end{aligned}$$

(2.15)

By (1.2), (2.14) and (2.15),

$$\begin{aligned} L(\widetilde{\gamma }_k)\le L(\gamma _k). \end{aligned}$$

(2.16)

Suppose (2.11) holds. Without loss of generality we may assume that $0\in \Omega _k$ for all $k\in {\mathbb {Z}}^+$. Then $B_{r_k}\subset \Omega _k$ for all $k\in {\mathbb {Z}}^+$. Hence by (2.9), (2.10),

$$\begin{aligned} A_{out}(\gamma _k)\le \text{ Vol }_g\left( {\mathbb {R}}^2{\setminus } B_{r_k}\right) \le \frac{A}{4} \quad \forall k\in {\mathbb {Z}}^+ \end{aligned}$$

(2.17)

and

$$\begin{aligned} \frac{3A}{4}\le \text{ Vol }_g\left( B_{r_k}\right) \le A_{in}(\gamma _k)\le A \quad \forall k\in {\mathbb {Z}}^+. \end{aligned}$$

(2.18)

We will now show that the circle $\widetilde{\gamma }_k=\partial B_{r_k}$ satisfies

$$\begin{aligned} I(\widetilde{\gamma }_k)\le I(\gamma _k). \end{aligned}$$

(2.19)

Let $\varepsilon =A_{out}(\widetilde{\gamma }_k)-A_{out}(\gamma _k)$. Then $\varepsilon =A_{in}(\gamma _k)-A_{in}(\widetilde{\gamma }_k)$. Since $\widetilde{\gamma }_k\subset \overline{\Omega }_k$ and the region between $\gamma _k$ and $\widetilde{\gamma }_k$ is contained in ${\mathbb {R}}^2{\setminus } B_{r_k}$, by (2.17),

$$\begin{aligned} 0\le \varepsilon \le \frac{A}{4}. \end{aligned}$$

(2.20)

Hence by (2.17) and (2.20),

$$\begin{aligned} \frac{1}{A_{in}(\widetilde{\gamma }_k)}+\frac{1}{A_{out}(\widetilde{\gamma }_k)} =&\frac{A}{A_{in}(\widetilde{\gamma }_k)A_{out}(\widetilde{\gamma }_k)} =\frac{A}{(A_{in}(\gamma _k)-\varepsilon )(A_{out}(\gamma _k)+\varepsilon )}\nonumber \\ \le&\frac{A}{A_{in}(\gamma _k)A_{out}(\gamma _k)} =\frac{1}{A_{in}(\gamma _k)}+\frac{1}{A_{out}(\gamma _k)}. \end{aligned}$$

(2.21)

By (2.16) and (2.21) we get (2.19). Now by (1.1),

$$\begin{aligned} A_{out}(\widetilde{\gamma }_k)=\int _{{\mathbb {R}}^2{\setminus } B_{r_k}}\sqrt{\text{ det }g_{ij}}\,dx \le 2\pi \int _{r_k}^{\infty }\rho \lambda _2(\rho )\,d\rho . \end{aligned}$$

(2.22)

By (1.3), (2.15), (2.19) and (2.22),

$$\begin{aligned} I(\gamma _k)\ge \frac{L(\widetilde{\gamma }_k)}{A_{out}(\widetilde{\gamma }_k)} +\frac{L(\widetilde{\gamma }_k)}{A_{in}(\widetilde{\gamma }_k)}\ge b_1. \end{aligned}$$

(2.23)

Letting $k\rightarrow \infty$ in (2.23),

$$\begin{aligned} I\ge b_1. \end{aligned}$$

(2.24)

This contradicts (1.9) and the definition of $b_0$. Hence (2.11) does not hold.

Suppose (2.12) holds. Without loss of generality we may assume that $0\in {\mathbb {R}}^2{\setminus }\Omega _k$ for all $k\in {\mathbb {Z}}^+$. Then by (2.10) $0\in {\mathbb {R}}^2{\setminus } \overline{\Omega }_k$ and $B_{r_k}\subset {\mathbb {R}}^2{\setminus }\overline{\Omega }_k$ for any $k\in {\mathbb {Z}}^+$. By an argument similar to the proof of (2.17) and (2.18) but with the role of $A_{in}(\gamma _k)$ and $A_{out}(\gamma _k)$ being interchanged in the proof we get

$$\begin{aligned} \left\{ \begin{aligned}&A_{in}(\gamma _k)\le \text{ Vol }_g\left( {\mathbb {R}}^2{\setminus } B_{r_k}\right) \le \frac{A}{4} \quad \forall k\in {\mathbb {Z}}^+\\&\frac{3A}{4}\le A_{out}(\gamma _k)\le A\qquad \qquad \quad \forall k\in {\mathbb {Z}}^+. \end{aligned}\right. \end{aligned}$$

(2.25)

Similarly by interchanging the role of $A_{in}(\gamma _k)$ and $A_{out}(\gamma _k)$ and replacing $\varepsilon$ by $\varepsilon ' =A_{out}(\widetilde{\gamma }_k)-A_{in}(\gamma _k)=A_{out}(\gamma _k) -A_{in}(\widetilde{\gamma }_k)$ in the proof of (2.19)–(2.23) above, we get that $0\le \varepsilon '\le A/4$ and (2.19), (2.23), still holds. Letting $k\rightarrow \infty$ in (2.23), we get (2.24). This again contradicts (1.9) and the definition of $b_0$. Thus (2.12) does not hold and Claim 1 follows. $\square$

We will now continue with the proof of the lemma. By Claim 1 there exists $k_0\in {\mathbb {Z}}^+$ such that

$$\begin{aligned}&\gamma _k\cap \left( {\mathbb {R}}^2{\setminus }\overline{B}_{c_0r_k}\right) =\emptyset \quad \forall k\ge k_0 \nonumber \\&\quad \Rightarrow \gamma _k\subset \overline{B}_{c_0r_k}{\setminus } B_{r_k} \quad \forall k\ge k_0. \end{aligned}$$

(2.26)

Note that either (2.11) or (2.12) holds. Suppose (2.11) holds. Without loss of generality we may assume that $0\in \Omega _k$ for all $k\ge k_0$. Then $B_{r_k}\subset \Omega _k$ for all $k\ge k_0$. Hence by (1.1) and (2.26),

$$\begin{aligned} L(\gamma _k)=&\int _0^{2\pi }\left( g_{ij}\overset{.}{\gamma }_k^i\overset{.}{\gamma }_k^j\right) ^{\frac{1}{2}}\,d\phi \nonumber \\ \ge&\sqrt{\lambda _1(c_0r_k)} \int _0^{2\pi }\left( \left( \frac{dr}{d\phi }\right) ^2+r^2\left( \frac{d\theta }{d\phi }\right) ^2\right) ^{\frac{1}{2}}\,d\phi \nonumber \\ \ge&2\pi r_k\sqrt{\lambda _1(c_0r_k)}\quad \forall k\ge k_0 \end{aligned}$$

(2.27)

and

$$\begin{aligned} A_{out}(\gamma _k)\le \int _{{\mathbb {R}}^2{\setminus } B_{r_k}}\sqrt{\text{ det }g_{ij}}\,dx \le 2\pi \int _{r_k}^{\infty }\rho \lambda _2(\rho )\,d\rho \quad \forall k\ge k_0. \end{aligned}$$

(2.28)

By (1.3), (2.27) and (2.28),

$$\begin{aligned} I(\gamma _k)\ge \frac{L(\gamma _k)}{A_{out}(\gamma _k)} \ge \frac{r_k\sqrt{\lambda _1(c_0r_k)}}{\int _{r_k}^{\infty }\rho \lambda _2(\rho )\,d\rho }\ge b_1\quad \forall k\ge k_0. \end{aligned}$$

(2.29)

Letting $k\rightarrow \infty$ in (2.29), we get (2.24). Since (2.24) contradicts (1.9) and the definition of $b_0$, (2.11) does not hold. Hence (2.12) holds. By (2.10) and (2.12) we may assume without loss of generality that $0\in {\mathbb {R}}^2{\setminus }\overline{\Omega }_k$ for all $k\ge k_0$. Then $B_{r_k}\subset {\mathbb {R}}^2{\setminus }\overline{\Omega }_k$ for all $k\ge k_0$. Hence $\Omega _k$ is contractible to a point in $\overline{B}_{c_0r_k}{\setminus } B_{r_k}$ for all $k\ge k_0$. By (1.1),

$$\begin{aligned} L(\gamma _k)=\int _0^{2\pi }\left( g_{ij}\overset{.}{\gamma }_k^i\overset{.}{\gamma }_k^j\right) ^{\frac{1}{2}}\,d\phi \ge \sqrt{\lambda _1(c_0r_k)}L_e(\gamma _k)\quad \forall k\ge k_0. \end{aligned}$$

(2.30)

By the isoperimetric inequality,

$$\begin{aligned} 4\pi |\Omega _k|\le L_e(\gamma _k)^2. \end{aligned}$$

(2.31)

Then by (2.30) and (2.31),

$$\begin{aligned} L(\gamma _k)\ge 2(\pi \lambda _1(c_0r_k)|\Omega _k|)^{\frac{1}{2}} \quad \forall k\ge k_0. \end{aligned}$$

(2.32)

Now

$$\begin{aligned} A_{in}(\gamma _k)=\int _{\Omega _k}\sqrt{\text{ det }g_{ij}}\,dx \le \lambda _2(r_k)|\Omega _k|\quad \forall k\ge k_0. \end{aligned}$$

(2.33)

By (1.5), (2.32) and (2.33),

$$\begin{aligned}&L(\gamma _k)\ge 2\pi ^{\frac{1}{2}}\left( \frac{\lambda _1(c_0r_k)}{\lambda _2(r_k)}\right) ^{\frac{1}{2}}A_{in}(\gamma _k)^{\frac{1}{2}} \ge 2(\pi \delta )^{\frac{1}{2}}A_{in}(\gamma _k)^{\frac{1}{2}} \quad \forall k\ge k_0\nonumber \\&\quad \Rightarrow \quad I(\gamma _k)\ge \frac{L(\gamma _k)}{A_{in}(\gamma _k)} \ge 2(\pi \delta )^{\frac{1}{2}}A_{in}(\gamma _k)^{-\frac{1}{2}} \quad \forall k\ge k_0. \end{aligned}$$

(2.34)

Since $\Omega _k\subset {\mathbb {R}}^2{\setminus } B_{r_k}$,

$$\begin{aligned} A_{in}(\gamma _k)\rightarrow 0\quad \text{ as } k\rightarrow \infty . \end{aligned}$$

(2.35)

Letting $k\rightarrow \infty$ in (2.34) by (2.35) we get $I=\infty$. This contradicts (1.9). Hence (2.12) does not hold and the lemma follows. $\square$

By Lemma 2.1 there exists a constant $a_1>r_0$ such that

$$\begin{aligned} r_k\le a_1\quad \forall k\in {\mathbb {Z}}^+. \end{aligned}$$

(2.36)

Lemma 2.2

$\gamma _k\in \overline{B}_{a_1^2}\quad \forall k\in {\mathbb {Z}}^+$.

Proof

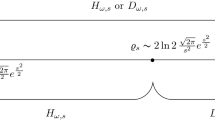
Let $\rho _k=\max _{\gamma _k}|x|$. Suppose the lemma does not hold. Then there exists a subsequence of $\rho _k$ which we may assume without loss of generality to be the sequence itself such that

$$\begin{aligned} \rho _k>a_1^2\quad \forall k\in {\mathbb {Z}}^+. \end{aligned}$$

(2.37)

By (1.1), (1.4), (2.36), (2.37) and an argument similar to the proof of (2.14),

$$\begin{aligned} L(\gamma _k)\ge \int _{a_1}^{a_1^2}\sqrt{\lambda _1(\rho )}\,d\rho \ge b_2 \quad \forall k\in {\mathbb {Z}}^+. \end{aligned}$$

(2.38)

Hence by (2.38),

$$\begin{aligned}&I(\gamma _k)=\frac{AL(\gamma _k)}{A_{in}(\gamma _k)A_{out}(\gamma _k)} \ge \frac{Ab_2}{(A/2)^2}=\frac{4b_2}{A}\quad \forall k\in {\mathbb {Z}}^+\\&\quad \Rightarrow I\ge \frac{4b_2}{A}\quad \text{ as } k\rightarrow \infty . \end{aligned}$$

This contradicts (1.9) and the definition of $b_0$. Hence the lemma follows. $\square$

Let $L_k=L(\gamma _k)$. Since $\overline{B}_{a_1^2}$ is compact, there exists constants $c_2>c_1>0$ such that

$$\begin{aligned} c_1\delta _{ij}\le g_{ij}\le c_2\delta _{ij}\quad \text{ on } \overline{B}_{a_1^2}. \end{aligned}$$

(2.39)

Lemma 2.3

There exists a constant $\delta _1>0$ such that $L_k\ge \delta _1\quad \forall k\in {\mathbb {Z}}^+$.

Proof

By (2.39),

$$\begin{aligned} \left\{ \begin{aligned}&c_1^{\frac{1}{2}}L_e(\gamma _k)\le L_k\le c_2^{\frac{1}{2}} L_e(\gamma _k)\quad \forall k\in {\mathbb {Z}}^+\\&c_1|\Omega _k|\le A_{in}(\gamma _k)\le c_2|\Omega _k|\quad \forall k\in {\mathbb {Z}}^+. \end{aligned}\right. \end{aligned}$$

(2.40)

By (2.8), (2.31) and (2.40),

$$\begin{aligned}&b_0>\frac{L_k}{A_{in}(\gamma _k)}\ge \frac{c_1^{\frac{1}{2}}L_e(\gamma _k)}{c_2|\Omega _k|}\ge \frac{c_1^{\frac{1}{2}}}{c_2}\cdot \frac{L_e(\gamma _k)}{(L_e(\gamma _k)^2/4\pi )}\ge \frac{4\pi c_1^{\frac{1}{2}}}{c_2L_e(\gamma _k)} \quad \forall k\in {\mathbb {Z}}^+\\&\Rightarrow \quad L_k\ge c_1^{\frac{1}{2}}L_e(\gamma _k) \ge \frac{4\pi c_1}{c_2b_0}\quad \forall k\in {\mathbb {Z}}^+ \end{aligned}$$

and the lemma follows. $\square$

By the proof of Lemma 2.3 we have the following corollary.

Corollary 2.4

For any constant $C_1>0$ there exists a constant $\delta _1>0$ such that

$$\begin{aligned} L(\gamma )>\delta _1 \end{aligned}$$

for any simple closed curve $\gamma \subset \overline{B}_{a_1^2}$ satisfying

$$\begin{aligned} I(\gamma )<C_1. \end{aligned}$$

(2.41)

By (1.6) and Corollary 2.4 we have the following corollary.

Corollary 2.5

For any constant $C_1>0$ there exists a constant $\delta _2>0$ such that

$$\begin{aligned} A_{in}(\gamma )>\delta _2\quad \text{ and } \quad A_{out}(\gamma )>\delta _2 \end{aligned}$$

for any simple closed curve $\gamma \subset \overline{B}_{a_1^2}$ satisfying (2.41).

Lemma 2.6

There exists a constant $C_2>0$ such that the following holds. Suppose $\beta \subset \overline{B}_{a_1^2}$ is a closed simple curve. Then under the curve shrinking flow

$$\begin{aligned} \frac{\partial \beta }{\partial \tau }(s,\tau )=k\vec {N} \end{aligned}$$

(2.42)

with $\beta (s,0)=\beta (s)$ where for each $\tau \ge 0$, $k(\cdot ,\tau )$ is the curvature, $\vec {N}$ is the unit inner normal, and s is the arc length of the curve $\beta (\cdot ,\tau )$ with respect to the metric g, there exists $\tau _0\ge 0$ such that the curve $\beta ^{\tau _0} =\beta (\cdot ,\tau _0)\subset \overline{B}_{a_1^2}$ satisfies $I(\beta ^{\tau _0}) \le I(\beta )$ and

$$\begin{aligned} \int k(s,\tau _0)^2\,ds\le C_2. \end{aligned}$$

Proof

Since the proof is similar to the proof of [2] and the Lemma on P.197 of [12], we will only sketch the proof here. Let $\beta ^{\tau } =\beta (\cdot ,\tau )$ and write

$$\begin{aligned} L(\tau )=L_g(\beta (\cdot ,\tau )),\,\, I(\tau )=I(\beta ^{\tau }) =I_g(\beta (\cdot ,\tau )), \end{aligned}$$

and the areas

$$\begin{aligned} A_{in}(\tau )=A_{in}(\beta (\cdot ,\tau )),\,\, A_{out}(\tau ) =A_{out}(\beta (\cdot ,\tau )), \end{aligned}$$

with respect to the metric g. Let $T_1>0$ be the maximal existence time of the solution of (2.42). Then

$$\begin{aligned} \beta ^{\tau }\subset \overline{B}_{a_1^2}\quad \forall 0\le \tau <T_1. \end{aligned}$$

(2.43)

Similar to the result on P.196 of [12] we have

$$\begin{aligned} \frac{\partial A_{in}}{\partial \tau }=-\int k\,ds, \quad \frac{\partial A_{out}}{\partial \tau } =\int k\,ds,\quad \frac{\partial L}{\partial \tau }=-\int k^2\,ds \end{aligned}$$

(2.44)

and

$$\begin{aligned} \int k\,ds+\int _{\Omega (\tau )} KdV_g=2\pi \end{aligned}$$

(2.45)

by the Gauss-Bonnet theorem where K is the Gauss curvature with respect to g and $\Omega (\tau )\subset \overline{B}_{a_1^2}$ is the region enclosed by the curve $\beta (s,\tau )$. Let $C_1=2I(\beta )$. By continuity there exists a constant $0<\delta _0<T_1$ such that

$$\begin{aligned} I(\tau )<C_1\quad \forall 0\le \tau \le \delta _0. \end{aligned}$$

(2.46)

By (2.46), Corollary 2.4, and Corollary 2.5 there exist constants $\delta _1>0$, $\delta _2>0$, such that

$$\begin{aligned} L(\tau )>\delta _1,\quad A_{in}(\tau )>\delta _2,\quad A_{out}(\tau )>\delta _2 \quad \forall 0\le \tau \le \delta _0. \end{aligned}$$

(2.47)

Now

$$\begin{aligned} \frac{\partial }{\partial \tau }(\log I(\tau ))=\frac{1}{L}\frac{\partial L}{\partial \tau } -\frac{1}{A_{in}}\frac{\partial A_{in}}{\partial \tau }-\frac{1}{A_{out}}\frac{\partial A_{out}}{\partial \tau }+\frac{1}{A}\frac{\partial A}{\partial \tau }. \end{aligned}$$

(2.48)

By (2.43) and (2.45) $\int k\,ds$ is uniformly bounded for all $0\le \tau <T_1$. Then by (2.44), (2.45), (2.47), and (2.48), there exists a constant $C_2>0$ independent of $\delta _0$ such that

$$\begin{aligned} \frac{\partial }{\partial \tau }(\log I(\tau ))<0 \end{aligned}$$

for any $\tau \in (0,\delta _0]$ satisfying

$$\begin{aligned} \int k(s,\tau )^2\,ds>C_2. \end{aligned}$$

If

$$\begin{aligned} \int k(s,0)^2\,ds\le C_2, \end{aligned}$$

we set $\tau _0=0$ and we are done. If

$$\begin{aligned} \int k(s,0)^2\,ds>C_2, \end{aligned}$$

then either there exists $\tau _0\in (0,\delta _0]$ such that

$$\begin{aligned} \int k(s,\tau _0)^2\,ds=C_2\quad \text{ and } \quad \int k(s,\tau )^2\,ds>C_2 \quad \forall 0\le \tau <\tau _0 \end{aligned}$$

(2.49)

or

$$\begin{aligned} \int k(s,\tau )^2\,ds>C_2\quad \forall 0\le \tau \le \delta _0. \end{aligned}$$

(2.50)

If (2.49) holds, since $I(\tau _0)\le I(0)$ we are done. If (2.50) holds, since $I(\delta _0)\le I(0)$ we can repeat the above the argument a finite number of times. Then either

(a) there exists $\tau _0\in (0,T_1)$ such that (2.49) holds

or

(b)

$$\begin{aligned} \int k(s,\tau )^2\,ds>C_2\quad \forall 0\le \tau <T_1 \end{aligned}$$

(2.51)

holds.

If (b) holds, then similar to the proof of the Lemma on P.197 of [12] by (2.47) we get a contradiction to the Grayson theorem ([9, 10, 12]) for curve shortening flow. Hence (a) holds. Since $I(\tau _0)\le I(0)$, the lemma follows. $\square$

To complete the proof of Theorem 1.1 we also need the following technical lemma (see [12]).

Lemma 2.7

For any positive numbers $\alpha _1,\alpha _2,A_1,A_2,A_3$ we have

$$\begin{aligned} (\alpha _1+\alpha _2)\left( \frac{1}{A_2}+\frac{1}{A_1+A_3}\right) \ge \min \left\{ \alpha _1\left( \frac{1}{A_1}+\frac{1}{A_2+A_3}\right) , \alpha _2\left( \frac{1}{A_3}+\frac{1}{A_1+A_2}\right) \right\} .\nonumber \\ \end{aligned}$$

(2.52)

Proof

Suppose (2.52) does not hold. Then

$$\begin{aligned}&(\alpha _1+\alpha _2)\left( \frac{1}{A_2}+\frac{1}{A_1+A_3}\right) \le \alpha _1\left( \frac{1}{A_1}+\frac{1}{A_2+A_3}\right) \nonumber \\&\quad \Rightarrow \quad \frac{A_1(A_2+A_3)}{A_2(A_1+A_3)} \le \frac{\alpha _1}{\alpha _1+\alpha _2} \end{aligned}$$

(2.53)

and

$$\begin{aligned}&(\alpha _1+\alpha _2)\left( \frac{1}{A_2}+\frac{1}{A_1+A_3}\right) \le \alpha _2\left( \frac{1}{A_3}+\frac{1}{A_1+A_2}\right) \nonumber \\&\quad \Rightarrow \quad \frac{A_3(A_1+A_2)}{A_2(A_1+A_3)} \le \frac{\alpha _2}{\alpha _1+\alpha _2}. \end{aligned}$$

(2.54)

Summing (2.53) and (2.54),

$$\begin{aligned} \frac{2A_1A_3}{A_2(A_1+A_3)}\le 0\quad \Rightarrow \quad A_1=0 \text{ or } A_3=0. \end{aligned}$$

Contradiction arises. Hence (2.52) holds and the lemma follows. $\square$

We are now ready for the proof of Theorem 1.1.

Proof of Theorem 1.1

Since the proof is similar to the proof of [11, 12] we will only sketch the argument here. Let $C_2>0$ be given by Lemma 2.6 and $\delta _1>0$ be given by Corollary 2.4 with $C_1=b_0$. By Lemma 2.2, Lemma 2.3, Corollary 2.4, Lemma 2.6 and an argument similar to the proof of [12] for each $j\in {\mathbb {Z}}^+$ there exists a closed simple curve $\overline{\gamma }_j\subset \overline{B}_{a_1^2}$ satisfying

$$\begin{aligned} I(\overline{\gamma }_j)\le I(\gamma _j)\quad \text{ and }\quad L(\overline{\gamma }_j) \ge \delta _1\quad \forall j\in {\mathbb {Z}}^+ \end{aligned}$$

and

$$\begin{aligned} \int _{\overline{\gamma }_j}k^2\,ds\le C_2, \end{aligned}$$

(2.55)

where k is the curvature of $\overline{\gamma }_j$. By (2.55) and the same argument as that on P. 197-199 of [12] $\overline{\gamma }_j$ are locally uniformly bounded in $L_2^1$ and $C^{1+\frac{1}{2}}$. Hence $\overline{\gamma }_j$ has a sequence which we may assume without loss of generality to be the sequence itself that converges uniformly in $L_p^1$ for any $1<p<2$ and in $C^{1+\alpha }$ for any $0<\alpha <1/2$ as $j\rightarrow \infty$ to some closed immersed curve $\gamma \subset \overline{B}_{a_1^2}$. Moreover $\gamma$ satisfies

$$\begin{aligned} I=I(\gamma )\quad \text{ and } \quad L(\gamma )\ge \delta _1. \end{aligned}$$

Since $\gamma$ is the limit of embedded curves, $\gamma$ cannot cross itself and at worst it will be self tangent. Suppose $\gamma$ is self tangent. Without loss of generality we may assume that $\gamma$ is only self tangent at one point. Then $\gamma =\beta _1\cup \beta _2$ with $\beta _1\cap \beta _2$ being a single point where $\beta _1$, $\beta _2$, are simple closed curves. Then $A_{in}(\gamma )=A_{in}(\beta _1)+A_{in}(\beta _2)$, $A_{out}(\beta _1)= A_{out}(\gamma )+A_{in}(\beta _2)$, $A_{out}(\beta _2)= A_{out}(\gamma )+A_{in}(\beta _1)$, and $L(\gamma )=L(\beta _1)+L(\beta _2)$. Let $L_1=L(\beta _1)$ and $L_2=L(\beta _2)$. By Lemma 2.7,

$$\begin{aligned}&(L_1+L_2)\left( \frac{1}{A_{out}(\gamma )} +\frac{1}{A_{in}(\beta _1)+A_{in}(\beta _2)}\right) \\&\quad \ge \min \left\{ L_1 \left( \frac{1}{A_{in}(\beta _1)}+\frac{1}{A_{out}(\gamma )+A_{in}(\beta _2)}\right) , L_2\left( \frac{1}{A_{in}(\beta _2)}+\frac{1}{A_{out}(\gamma ) +A_{in}(\beta _1)}\right) \right\} . \end{aligned}$$

Hence

$$\begin{aligned}&L(\gamma )\left( \frac{1}{A_{out}(\gamma )}+\frac{1}{A_{in}(\gamma )}\right) \\&\quad \ge \min \left\{ L_1\left( \frac{1}{A_{in}(\beta _1)}+\frac{1}{A_{out}(\beta _1)} \right) , L_2\left( \frac{1}{A_{in}(\beta _2)}+\frac{1}{A_{out}(\beta _2)}\right) \right\} \\&\quad \Rightarrow \quad I(\gamma )\ge \min (I(\beta _1),I(\beta _2))\\&\quad \Rightarrow \quad I(\gamma )=\min (I(\beta _1),I(\beta _2)). \end{aligned}$$

Without loss of generality we may assume that $I(\gamma )=I(\beta _1)$. Then by Corollary 2.4 $\beta _1$ is a simple closed curve which attains the minimum. Similar to the proof of [12], by a variation argument $\beta _1$ has constant curvature

$$\begin{aligned} k=L\left( \frac{1}{A_{in}}-\frac{1}{A_{out}}\right) . \end{aligned}$$

Hence $\beta _1$ is smooth and the theorem follows. $\square$