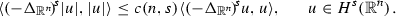Abstract
We study the Nemytskii operators \(u\mapsto |u|\) and \(u\mapsto u^{\pm }\) in fractional Sobolev spaces \(H^s({\mathbb {R}}^n)\), \(s>1\).
Similar content being viewed by others
1 Introduction and main result
In this paper we discuss the relation between the map \(u\mapsto |u|\) and the Dirichlet Laplacian. Recall that the Dirichlet Laplacian  of order \(s>0\) of a function \(u\in L^2({\mathbb {R}}^n)\), \(n\ge 1\), is the distribution
of order \(s>0\) of a function \(u\in L^2({\mathbb {R}}^n)\), \(n\ge 1\), is the distribution

where

is the Fourier transform in \({\mathbb {R}}^n\). The Sobolev–Slobodetskii space
naturally inherits an Hilbertian structure from the scalar product

The standard reference for the operator  and functions in \(H^s({\mathbb {R}}^n)\) is the monograph [8] by Triebel.
and functions in \(H^s({\mathbb {R}}^n)\) is the monograph [8] by Triebel.
For any positive order \(s\notin \mathbb N\) we introduce the constant

Notice that
where \( \lfloor s\rfloor \) stands for the integer part of s. It is well known that for \(s\in (0,1)\) and \(u,v\in H^s({\mathbb {R}}^n)\) one has

Let us recall some known facts about the Nemytskii operator \(|\cdot |: u\mapsto |u|\).
-
1.
\(|\cdot |\) is a Lipschitz transform of \(H^0({\mathbb {R}}^n)\equiv L^2({\mathbb {R}}^n)\) into itself.
-
2.
Let \(0<s\le 1\). Then \(| \cdot |\) is a continuous transform of \(H^s({\mathbb {R}}^n)\) into itself, by general results about Nemytskii operators in Sobolev/Besov spaces, see [7, Theorem 5.5.2/3]. Also it is obvious that for \(u\in H^1({\mathbb {R}}^n)\)
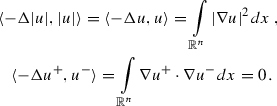
Here and elsewhere \(u^{\pm }=\max \{\pm u,0\}=\frac{1}{2}(|u|\pm u)\), so that \(u=u^+-u^-\), \(|u|=u^++u^-\). On the other hand, for \(s\in (0,1)\) and \(u\in H^s({\mathbb {R}}^n)\) formula (3) gives
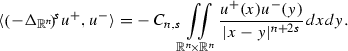 (4)
(4)From (4) we infer by the polarization identity
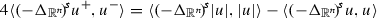
that if u changes sign then
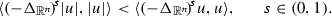 (5)
(5)We mention also [4, Theorem 6] for a different proof and explanation of (5), that includes the case when
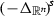 is replaced by the Navier (or spectral Dirichlet) Laplacian on a bounded Lipschitz domain \(\Omega \subset {\mathbb {R}}^n\).
is replaced by the Navier (or spectral Dirichlet) Laplacian on a bounded Lipschitz domain \(\Omega \subset {\mathbb {R}}^n\). -
3.
Let \(1<s<\frac{3}{2}\). The results in [2] and [6] (see also Section 4 of the exhaustive survey [3]) imply that \(| \cdot |\) is a bounded transform of \(H^s({\mathbb {R}}^n)\) into itself. That is, there exists a constant c(n, s) such that
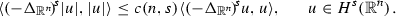
In particular, \(|\cdot |\) is continuous at \(0\in H^s({\mathbb {R}}^n)\).
It is easy to show that the assumption \(s<\frac{3}{2}\) can not be improved, see Example 1 below and [2, Proposition p. 357], where a more general setting involving Besov spaces \(B^{s,q}_p({\mathbb {R}}^n)\), \(s\ge 1+\frac{1}{p}\), is considered.
At our knowledge, the continuity of \(|\cdot |: H^s({\mathbb {R}}^n)\rightarrow H^s({\mathbb {R}}^n)\), \(s\in (1,\frac{3}{2})\), is an open problem. We can only point out the next simple result.
Proposition 1
Let \(0<\tau<s<\frac{3}{2}\). Then \(|\cdot |:H^s({\mathbb {R}}^n)\rightarrow H^\tau ({\mathbb {R}}^n)\) is continuous.
Proof
Recall that \(H^s({\mathbb {R}}^n)\hookrightarrow H^\tau ({\mathbb {R}}^n)\) for \(0<\tau <s\). Actually, the Hölder inequality readily gives the well known interpolation inequality

Since \(|\cdot |\) is continuous \(L^2({\mathbb {R}}^n)\rightarrow L^2({\mathbb {R}}^n)\) and bounded \(H^s({\mathbb {R}}^n)\rightarrow H^s({\mathbb {R}}^n)\), the statement follows immediately. \(\square \)
Now we formulate our main result. It provides the complete proof of [5, Theorem 1] for s below the threshold \(\frac{3}{2}\) and gives a positive answer to a question raised in [1, Remark 4.2] by Nicola Abatangelo, Sven Jahros and Albero Saldaña.
Theorem 1
Let \(s\in (1,\frac{3}{2})\) and \(u \in H^s({\mathbb {R}}^n)\). Then formula (4) holds. In particular, if u changes sign then

Our proof is deeply based on the continuity result in Proposition 1. The knowledge of continuity of \(|\cdot |: H^s({\mathbb {R}}^n)\rightarrow H^s({\mathbb {R}}^n)\) could considerably simplify it.
We denote by c any positive constant whose value is not important for our purposes. Its value may change line to line. The dependance of c on certain parameters is shown in parentheses.
2 Preliminary results and proof of Theorem 1
We begin with a simple but crucial identity that has been independently pointed out in [5, Lemma 1] and [1, Lemma 3.11] (without exact value of the constant). Notice that it holds for general fractional orders \(s>0\).
Theorem 2
Let \(s>0\), \(s\notin \mathbb N\). Assume that \(v,w\in H^s({\mathbb {R}}^n)\) have compact and disjoint supports. Then

Proof
Let \(\rho _h\) be a sequence of mollifiers, and put \({w}_h:={w}*\rho _h\). Formula (3) gives

Since for large h the supports of v and \(w_h\) are separated, we have

Here we can integrate by parts. Using (1) one computes for \(a>0\)
and obtains (6) with \(w_h\) instead of w.
Since the supports of v and w are separated, it is easy to pass to the limit as \(h\rightarrow \infty \) and to conclude the proof. \(\square \)
Remark 1
Motivated by (6) and (2), A.I. Nazarov conjectured in [5] that

for any not integer exponent \(s>0\) and for any changing sign function \(u\in H^s({\mathbb {R}}^n)\) such that \(u^\pm \in H^s({\mathbb {R}}^n)\).
Lemma 1
Let \(s\in (1,\frac{3}{2})\) and \(\varepsilon >0\). If a function \(u\in H^s({\mathbb {R}}^n)\) has compact support then \((u-\varepsilon )^+\in H^s({\mathbb {R}}^n)\), and

Proof
Take a nonnegative function \(\eta \in \mathcal{C}^\infty _0({\mathbb {R}}^n)\) such that \(\eta \equiv 1\) on \(\mathrm{supp}(u)\). Clearly \(u-\varepsilon \eta \in H^s({\mathbb {R}}^n)\). Hence, by Item 3 in the Introduction we have that \((u-\varepsilon \eta )^+=(u-\varepsilon )^+\in H^s({\mathbb {R}}^n)\) and

The proof is complete. \(\square \)
In order to simplify notation, for \(u:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) and \(s>0\) we put

Lemma 2
Let \(s\in (1,\frac{3}{2})\) and \(u\in H^s({\mathbb {R}}^n)\cap \mathcal{C}^0_0({\mathbb {R}}^n)\). Then (4) holds, and in particular \(\displaystyle {\Phi ^s_u\in L^1({\mathbb {R}}^n\times {\mathbb {R}}^n)}\).
Proof
Thanks to Lemma 1 we have that \((u^--\varepsilon )^+ \in H^s({\mathbb {R}}^n)\cap \mathcal{C}^0_0({\mathbb {R}}^n)\) for any \(\varepsilon >0\). Next, the supports of the functions \(u^+\) and \((u^--\varepsilon )^+\) are compact and disjoint. Thus we can apply Theorem 2 to get

Take a decreasing sequence \(\varepsilon \searrow 0\). From Lemma 1 we infer that \((u^--\varepsilon )^+\rightarrow u^-\) weakly in \(H^s({\mathbb {R}}^n)\), as \((u^--\varepsilon )^+\rightarrow u^-\) in \(L^2({\mathbb {R}}^n)\). Hence the duality product in (7) converges to the the duality product in (4). Next, the integrand in the right-hand side of (7) increases to \(\Phi ^s_u\) a.e. on \({\mathbb {R}}^n\times {\mathbb {R}}^n\). By the monotone convergence theorem we get the convergence of the integrals, and the conclusion follows immediately. \(\square \)
Lemma 3
Let \(s\in (1,\frac{3}{2})\) and \(u\in H^s({\mathbb {R}}^n)\). Then \(\displaystyle {\Phi ^s_u\in L^1({\mathbb {R}}^n\times {\mathbb {R}}^n)}\).
Proof
Take a sequence of functions \(u_h\in \mathcal{C}^\infty _0({\mathbb {R}}^n)\) such that \(u_h\rightarrow u\) in \(H^s({\mathbb {R}}^n)\) and almost everywhere. Since \(\displaystyle {\Phi ^s_{u_h}\rightarrow \Phi ^s_u}\) a.e. on \({\mathbb {R}}^n\times {\mathbb {R}}^n\), Fatou’s Lemma, Lemma 2 for \(u_h\) and the boundeness of \(v\mapsto v^\pm \) in \(H^s({\mathbb {R}}^n)\) give

that concludes the proof. \(\square \)
Proof of Theorem 1
Take a sequence \(u_h\in \mathcal{C}^\infty _0({\mathbb {R}}^n)\) such that \(u_h\rightarrow u\) in \(H^s({\mathbb {R}}^n)\) and almost everywhere. Consider the nonnegative functions
Then \(v_h, w_h\in H^s({\mathbb {R}}^n)\). Next, take any exponent \(\tau \in (1,s)\). By Proposition 1 we have that \(u^\pm -u^\pm _h\rightarrow 0\) in \(H^\tau ({\mathbb {R}}^n)\); hence \((u^\pm -u^\pm _h)^+\rightarrow 0\) in \(H^\tau ({\mathbb {R}}^n)\) by Item 3 in the Introduction. Thus,
Now we take a small \(\varepsilon >0\). Recall that \((v_h-\varepsilon )^+ \in H^\tau ({\mathbb {R}}^n)\) by Lemma 1. Moreover, from \(0\le v_h \le u_h^+\), \(0\le w_h\le u_h^-\) it follows that
In particular, the functions \((v_h-\varepsilon )^+, w_h\) have compact and disjoint supports. Thus we can apply Theorem 2 to infer

We first take the limit as \(\varepsilon \searrow 0\). The argument in the proof of Lemma 2 gives

Next we push \(h\rightarrow \infty \). By (8) we get

Further, since the integrand in the right-hand side of (9) does not exceed \(\Phi ^\tau _u(x,y)\), Lemma 3, (8) and Lebesgue’s theorem give

Thus, we proved (4) with s replaced by \(\tau \). It remains to pass to the limit as \(\tau \nearrow s\). By Lebesgue’s theorem, we have

Now we fix \(\tau _0\in (1,s)\) and notice that \(0\le \Phi ^\tau _u \le \max \{\Phi ^{\tau _0}_u,\Phi ^s_u\}\) for any \(\tau \in (\tau _0,s)\). Therefore, Lemma 3 and Lebesgue’s theorem give

The proof of (4) is complete. The last statement follows immediately from (4), polarization identity and (2). \(\square \)
Example 1
It is easy to construct a function \(u\in \mathcal{C}^\infty _0({\mathbb {R}}^n)\) such that \(u^+\in H^s({\mathbb {R}}^n)\) if and only if \(s<\frac{3}{2}\).
Take \(\varphi \in \mathcal{C}^\infty _0({\mathbb {R}})\) satisfying \(\varphi (0)=0, \varphi '(0)> 0\) and \(x\varphi (x)\ge 0\) on \({\mathbb {R}}\). By direct computation one checks that \(\varphi ^+=\chi _{(0,\infty )}\varphi \in H^s({\mathbb {R}})\) if and only if \(s<\frac{3}{2}\). If \(n=1\) we are done. If \(n\ge 2\) we take \(u(x_1,x_2,\dots , x_n)=\varphi (x_1)\varphi (x_2)\dots \varphi (x_n)\).
References
Abatangelo, N., Jarohs, S., Saldaña, A.: On the maximum principle for higher-order fractional Laplacians, preprint arxiv:1607.00929 (2016)
Bourdaud, G., Meyer, Y.: Fonctions qui opèrent sur les espaces de Sobolev. J. Funct. Anal. 97(2), 351–360 (1991)
Bourdaud, G., Sickel, W.: Composition operators on function spaces with fractional order of smoothness. In: Ozawa, T., Sugimoto, M. (eds.) Harmonic Analysis and Nonlinear Partial Differential Equations, pp. 93–132 RIMS Kokyuroku Bessatsu, B26, Res. Inst. Math. Sci. (RIMS), Kyoto (2011)
Musina, R., Nazarov, A.I.: On the Sobolev and Hardy constants for the fractional Navier Laplacian, Nonlinear Anal. 121 (2015), 123–129. http://www.sciencedirect.com/science/article/pii/S0362546X14003113
Nazarov, A.I.: Remark on fractional Laplacians, SPbMS El. Prepr. archive:N 2016-01. p.4
Oswald, P.: On the boundedness of the mapping \(f\rightarrow \vert f\vert \) in Besov spaces. Comment. Math. Univ. Carolin. 33(1), 57–66 (1992)
Runst, T., Sickel, W.: Sobolev Spaces of Fractional Order, Nemytskij Operators, and Nonlinear Partial Differential Equations, de Gruyter Series in Nonlinear Analysis and Applications, 3. de Gruyter, Berlin (1996)
Triebel, H.: Interpolation Theory, Function Spaces, Differential Operators. Deutscher Verlag Wissensch, Berlin (1978)
Acknowledgements
The first author wishes to thank Université Libre de Bruxelles for the hospitality in February 2016. She is grateful to Denis Bonheure, Nicola Abatangelo, Sven Jahros and Albero Saldaña for valuable discussion on this subject.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ari Laptev.
Roberta Musina: Partially supported by Miur-PRIN 2015233N54.
Alexander I. Nazarov: Supported by RFBR Grant 17-01-00678.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Musina, R., Nazarov, A.I. A note on truncations in fractional Sobolev spaces. Bull. Math. Sci. (2017). https://doi.org/10.1007/s13373-017-0107-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13373-017-0107-8




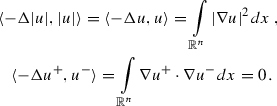
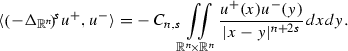
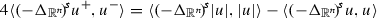
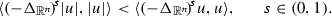
 is replaced by the Navier (or spectral Dirichlet) Laplacian on a bounded Lipschitz domain
is replaced by the Navier (or spectral Dirichlet) Laplacian on a bounded Lipschitz domain