Effective Prandtl Number Model Influences on the $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {H}}_2 {\hbox {O}}$ and $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {C}}_2 {\hbox {H}}_6 {\hbox {O}}_2$ Nanofluids Spray Along a Stretching Cylinder

Abstract

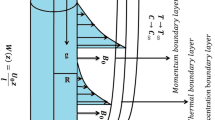
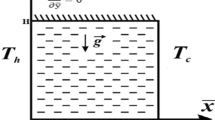
The flow of common fluids (water, oils and ethylene glycol etc.) is diluted by adding different small particles of metals, and their oxides are more powerful to reduce the scientific issues related to quicker heat transfer. According to this indication, we have contemplated finite film of $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {H}}_2 {\hbox {O}}$ and $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {C}}_2 {\hbox {H}}_6 {\hbox {O}}_2$ nanoliquid sprayed on an extending cylinder. In this scenario, uniform magnetic field $B_0$ and constant reference temperature are employed on the stream of thin film nanofluid. The impact of effective Prandtl number, viscosity and thermal conductivity is derived from the experimental data (Sheikhzadeh et al. in J Appl Fluid Mech 10:209–219, 2017; Lee et al. in J Heat transf 121:280–289, 1992; Wang et al. in J Thermo Phys Heat Transf 13:474–480, 1999; Hamilton and Crosser in Ind Eng Chem Fundam 1:187–191, 1962; Maiga et al. in Super Lattices Microstruct 35:543–55, 2004; Hayat et al. in J Mol Liq. https://doi.org/10.1016/j.molliq.2018.06.029, 2018). The model problem is excellently converted into a set of proper self-comparable forms with the assistance of possible transformations. Analytical results of velocity and thermal profile are computed using homotopy analysis method for both $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {H}}_2 {\hbox {O}}$ and $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {C}}_2 {\hbox {H}}_6 {\hbox {O}}_2$ nanoliquid. Furthermore, during coating analysis, rate of spray, pressure distribution, skin friction coefficient (surface drag force) $C_{\mathrm{f}}$ and Nusselt number (the rate of heat transfer) Nu for both nanofluids are also intended. The impact of additional ingrained quantities like magnetic parameter M, volume fraction of nanoparticles $\varphi$, Grashof number Gr, fluid thickness parameter $\beta$, Prandtl number Pr and Reynolds number Re is portrayed numerically and graphically for both alumina particles. The key observation indicates that the temperature of $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {C}}_2 {\hbox {H}}_6 {\hbox {O}}_2$ nanoliquid leading on $\gamma {\hbox {Al}}_2 {\hbox {O}}_3$–${\hbox {H}}_2 {\hbox {O}}$ nanoliquid during the study. Due to greater viscosity and thermal conductivity, ${\hbox {C}}_2 {\hbox {H}}_6 {\hbox {O}}_2$-based nanofluid is observed as upgraded common base fluid assimilated to ${\hbox {H}}_2$O.