Abstract
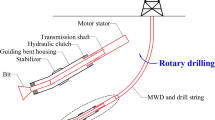
Abundant drilling activities had confirmed that the fully rotary drilling can improve the rate of penetration effectively. However, the fully rotary drilling has brought some challenges for the trajectory control ability of the bottom hole assembly (BHA). One of the reasons is the effect of drill-string rotation was ignored in the existing methods, where the bent-housing positive displacement motor (PDM) was regarded as the prebending beam. According to the D’Alembert principle, the dynamical centrifugal force, generated by drill-string rotation, was equivalent to a quasi-static problem. The mechanical model of BHA with bent-housing PDM was established based on the Timoshenko beam theory. The calculated formula of bit side force (BSF) and resultant steering force (RSF) was deduced. The influences of inclination, rotational speed of drill-string, bend angle, eccentricity, stabilizer, weight on bit (WOB) and elbow position on the average BSF and RSF were investigated. The results show that the rotational speed of drill-string has a significant influence on the steering ability. The average BSF increases with the rotational speed of drill-string, while the RSF increases firstly and decreases subsequently. The controlling factor is the transverse component of drill-string gravity in a low rotational speed, while it is the centrifugal force in a high rotational speed. The BSF climbs up and then declines with WOB and rotational speed of drill-string. When the rotational speed of drill-string exceeds 100 RPM or WOB is higher than 80 kN, the BSF will decrease, resulting in a decline in angle buildup. The present method can be utilized to optimize the drilling parameters, BHA configuration and structure of bent-housing PDM.
Similar content being viewed by others
Abbreviations
- ABPV:
-
Arrow back pressure valve
- AKO:
-
Adjustable kick-off
- BHA:
-
Bottom hole assembly
- BSF:
-
Bit side force
- CA:
-
Closured azimuth
- CD:
-
Closured displacement
- DC:
-
Drill collar
- DKF:
-
Double kick-off
- DTU:
-
Double-tilted universal
- FAB:
-
Fixed angle build
- HWDP:
-
Heavy weight drill pipe
- MD:
-
Measured depth
- MWD:
-
Measurement while drilling
- NMDC:
-
Non-magnetic drill collar
- NPT:
-
Nonproductive time
- PDM:
-
Positive displacement motor
- PDC:
-
Polycrystalline diamond compact
- ROP:
-
Rate of penetration
- RPM:
-
Revolutions per minute
- RSF:
-
Resultant steering force
- RSDS:
-
Rotary steerable drilling system
- TVD:
-
True vertical depth
- WOB:
-
Weight on bit
- \(\gamma \) :
-
Bending angle \(({^{\circ }})\)
- \(\alpha \) :
-
Inclination angle of well \(({^{\circ }})\)
- \(\theta \) :
-
The angle between the drill-string and borehole axis \(({^{\circ }})\)
- c :
-
The length between the elbow point and first stabilizer (m)
- e :
-
Eccentricity (mm)
- F :
-
Equivalent concentrated force of bent-housing PDM (N)
- b :
-
The distance between the load F and first stabilizer (m)
- E :
-
Young’s modulus (GPa)
- \(F_\mathrm{cen}\) :
-
Concentrated centrifugal force (N)
- y :
-
Deflection of drill-string (mm)
- \(P_{1}\) :
-
Axial force of the first stabilizer (N)
- \(P_{2}\) :
-
Axial force of the second stabilizer (N)
- \(F_{1}\), \(F_{2}\) :
-
Support reaction of the 1st and 2nd stabilizer (N)
- \(m_{1}\), \(m_{2}\), \(m_{3}\) :
-
Linear density of the 1st, 2nd and 3rd span (kg/m)
- w :
-
Rotational speed (rpm)
- \(l_{1}\), \(l_{2}\), \(l_{3}\) :
-
Length of the 1st, 2nd and 3rd span (m)
- \(P_{b}\) :
-
WOB (kN)
- \(q_{2}\) :
-
Uniform transverse load of drill-string (N/m)
- M(x):
-
Bending moment of any position \((\hbox {N}\cdot \hbox {m})\)
- \(X(u_{i})\) :
-
Transcendental function about \(u_{i}\)
- \(Y(u_{i})\) :
-
Transcendental function about \(u_{i}\)
- \(Z(u_{i})\) :
-
Transcendental function about \(u_{i}\)
- \(u_{i}\) :
-
Stability coefficient of drill-string
- i :
-
The order of the span
- \(M_{0}\), \(M_{3}\) :
-
Bending moment on the drill bit and upper tangent point (N \(\cdot \) m)
- \(M_{1}\), \(M_{2}\) :
-
Internal moment acted on the 1st and 2nd stabilizer (N \(\cdot \) m)
- \(D_{w}, \, D_{b}\),:
-
Diameter of the wellbore and drill bit (mm)
- \(D_{s1}\), \(D_{s2}\) :
-
Diameter of the 1st and 2nd stabilizer (mm)
- \(D_\mathrm{dc}\) :
-
Diameter of the drill collar (mm)
- \(e_{0}\), \(e_{3}\) :
-
Eccentricity locates at the drill bit and drill collar (mm)
- \(e_{1}\), \(e_{2}\) :
-
Eccentricity locates at the 1st and 2nd stabilizer (mm)
- \(I_{1}\), \(I_{2}\), \(I_{3}\) :
-
Inertia moment of the 1st, 2nd and 3rd span \((\hbox {m}^{4})\)
- \(P_{a}\) :
-
BSF value (N)
- \(\beta \) :
-
The angle between BSF and n-direction \(({^{\circ }})\)
- \(M_{o1}^n , M_{o1}^v \) :
-
Component of bending moment (N \(\cdot \) m)
- \(P_a ^{n}, P_a^v \) :
-
Component of BSF (N)
- \(\bar{{P}}_a \) :
-
Average BSF (N)
- \(F_{a}\) :
-
RSF value (N)
- \(L_{1}\) :
-
The distance between bent-sub and first stabilizer (m)
- \(L_{2}\) :
-
The distance between bent-sub and second stabilizer (m)
- \(R_{1}\) :
-
The radius of drill-string between bent-sub and first stabilizer (m)
- \(R_{2}\) :
-
The radius of drill-string between bent-sub and second stabilizer (m)
- \(d_{1}\) :
-
Maximum deflection between bent-sub and first stabilizer (m)
- \(d_{2}\) :
-
Maximum deflection between bent-sub and second stabilizer (m)
- N :
-
Node number of a circle
- \(\theta _{1}\) :
-
The angle of the segment between bent-sub and first stabilizer \(({^{\circ }})\)
- \(\theta _{2}\) :
-
The angle of the segment between bent-sub and second stabilizer \(({^{\circ }})\)
- k :
-
Buildup rate (\({^{\circ }}\)/30m)
References
Ma, T.; Chen, P.; Yang, C.; Zhao, J.: Wellbore stability analysis and well path optimization based on the breakout width model and Mogi–Coulomb criterion. J. Petrol. Sci. Eng. 135, 678–701 (2015)
Zou, C.; Zhai, G.; Zhang, G.; Wang, H.; Zhang, G.; Li, J.; Wang, Z.; Wen, Z.; Ma, F.; Liang, Y.; Yang, Z.; Li, X.; Liang, K.: Formation, distribution, potential and prediction of global conventional and unconventional hydrocarbon resources. Petrol. Explor. Dev. 42(1), 14–28 (2015)
Chen, P.: Drilling and Completion Engineering, 2nd edn. Petroleum Industry Press, China (2011)
Han, Z.: Design and Calculation of Directional Drilling, 2nd edn. China University of Petroleum Press, China (2011)
Gupta, V.P.; Yeap, A.H.P.; Fischer, K.M.; Mathis, R.S.; Egan, M.J.: Expanding the extended reach envelope at Chayvo Field, Sakhalin Island. In: IADC/SPE Drilling Conference and Exhibition. Society of Petroleum Engineers, SPE 168055 (2014)
Liu, Y.; Chen, P.; Wang, X.; Ma, T.: Modeling friction-reducing performance of an axial oscillation tool using dynamic friction model. J. Nat. Gas Sci. Eng. 33, 397–404 (2016)
Ma, T.; Chen, P.; Zhao, J.: Overview on vertical and directional drilling technologies for the exploration and exploitation of deep petroleum resources. Geomech. Geophys. Geo-Energy Geo-Resourc. 2(3), 365–395 (2016)
Ma, T.; Chen, P.; Zhang, Q.; Zhao, J.: A novel collapse pressure model with mechanical–chemical coupling in shale gas formations with multi-weakness planes. J. Nat. Gas Sci. Eng. 36, 1151–1177 (2016)
Ma, T.; Zhang, Q.B.; Chen, P.; Yang, C.; Zhao, J.: Fracture pressure model for inclined wells in layered formations with anisotropic rock strengths. J. Petrol. Sci. Eng. 149, 393–408 (2017)
Wang, X.; Chen, P.; Ma, T.; Liu, Y.: Modeling and experimental investigations on the drag reduction performance of an axial oscillation tool. J. Nat. Gas Sci. Eng. 39, 118–132 (2017)
Zhang, J.; Liang, Z.; Han, C.: Failure analysis and finite element simulation of key components of PDM. Eng. Fail. Anal. 45, 15–25 (2014)
Lubinski, A.: A study of the buckling of rotary drilling strings. In: Drilling and Production Practice. American Petroleum Institute, API-50-178 (1950)
Walker, B.H.; Friedman, M.B.: Three-dimensional force and deflection analysis of a variable cross section drill string. J. Pressure Vessel Technol. 99(2), 367–373 (1977)
Ho, H.S.: General formulation of drillstring under large deformation and its use in BHA analysis. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, SPE 15562 (1986)
Birades, M.: Static and dynamic three-dimensional bottomhole assembly computer models. SPE Drill. Eng. 3(2), 160–166 (1988)
Li, Z.; Liu, X.: Static behavior of bottom hole assembly under large deflection in 3-D curved borehole. J. Univ. Petrol. China 18(4), 37–42 (1994)
Gao, D.; Xu, B.: Three-dimensional analysis of the static behavior of BHA under large deflection. Chin. J. Appl. Mech. 12(1), 53–62 (1995)
Li, Z.: Theory of Well Trajectory Control. Petroleum Industry Press, China (1996)
Li, Z.: Research advances and debates on tubular mechanics in oil and gas wells. Acta Petrol. Sinica 37(4), 531–556 (2016)
Di, Q.; Yue, Y.; Peng, G.: Sliding guide assembly composite drilling force calculation and impact parameters. Petrol. Drill. Tech. 29(3), 56–57 (2001)
Di, Q.; Zhu, W.; Yao, J.; Zou, H.: The dynamical model of pre-bending BHA. Acta Petrol. Sinica 28(6), 118–121 (2007)
Di, Q.; Wang, W.; Yao, Y.; Zhu, W.; Yao, J.; Hu, Y.: Dynamics model of BHA and the characteristics simulation of vortex motion. J. China Univ. Petrol. (Edition of Natural Sciences) 34(3), 53–56 (2010)
Li, C.; Ding, T.; Wang, P.: An experimental rig for near-bit force measurement and drillstring acoustic transmission of BHA. Measurement 44(4), 642–652 (2011)
Hu, Y.; Di, Q.; Zhu, W.; Chen, Z.; Wang, W.: Dynamic characteristics analysis of drillstring in the ultra-deep well with spatial curved beam finite element. J. Petrol. Sci. Eng. 82(2), 166–173 (2012)
Ertas, D.; Bailey, J.R.; Wang, L.; Pastusek, P.E.: Drillstring mechanics model for surveillance, root cause analysis, and mitigation of torsional vibrations. SPE Drill. Complet. 29(4), 405–417 (2014)
Hareland, G.; Wu, A.; Lei, L.: The field tests for measurement of downhole weight on bit (DWOB) and the calibration of a real-time DWOB Model. In: International Petroleum Technology Conference. International Petroleum Technology Conference, IPTC 17503 (2014)
Yin, H.; Si, M.; Wang, R.; Liu, H.: A model based on orthogonal regression analysis for prediction of build rates in compound drilling in long horizontal section. Pak. J. Stat. 30(6), 1081–1092 (2014)
Wood, D.A.: Drilling and borehole techniques relevant to natural gas exploration and development: a collection of published research (2009–2015). J. Nat. Gas Sci. Eng. 26, 396–408 (2015)
Hu, L.; Gao, D.: A new orientation design model and numerical solution for coiled tubing drilling. J. Nat. Gas Sci. Eng. 22, 656–660 (2015)
Huang, W.; Gao, D.; Wei, S.; Li, X.: A generalized quasi-static model of drill string system. J. Nat. Gas Sci. Eng. 23, 208–220 (2015)
Huang, W.; Gao, D.; Wei, S.: Local mechanical model of down-hole tubular strings constrained in curved wellbores. J. Petrol. Sci. Eng. 129, 233–242 (2015)
Millheim, K.K.; Apostal, M.C.: The effect of bottomhole assembly dynamics on the trajectory of a bit. J. Petrol. Technol. 33(12), 2323–2338 (1981)
Bai, J.; Su, Y.: Theory and Practice of Well Deviation Control. Petroleum Industry Press, China (1990)
Gao, D.: Down-Hole Tubular Mechanics and its Application. University of Petroleum Press, Dongying (2006)
Li, Z.; Zhang, C.; Song, G.: Research advances and debates on tubular mechanics in oil and gas wells. J. Petrol. Sci. Eng. 151, 194–212 (2016)
Su, Y.; Tang, X.; Chen, Z.: Equivalent loading method for solving beam-column with initial bending and its application in drilling engineering. Mech. Eng. 26(1), 42–44 (2004)
Tang, X.; Su, Y.; Chen, Z.: Beam-column theory for bent housing PDM assemblies with medium-short radius of building capability. Mech. Eng. 33(3), 20–24 (2011)
Liu, X.: A practical method for calculating the geometric build-up rate of steerable BHA. Nat. Gas. Ind. 25(11), 50–52 (2005)
Acknowledgements
This work was financially supported by the Major National Science and Technology Projects of China (Grant No. 2016ZX05022-001), the 973 Program of China (Grant No. 2013CB228003), the Science and Technology Support Program of Sichuan Province (Grant No. 2015SZ0003), and the Funds of State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation of Southwest Petroleum University (Grant Nos. PLN201611 and G201604).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Liu, H., Ma, T., Chen, P. et al. Mechanical Behaviors of Bottom Hole Assembly with Bent-Housing Positive Displacement Motor Under Rotary Drilling. Arab J Sci Eng 44, 6029–6043 (2019). https://doi.org/10.1007/s13369-017-2564-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13369-017-2564-5