Skip to main content
SpringerLink
Log in

Boundary smoothness of analytic functions

  • Published:
Analysis and Mathematical Physics Aims and scope Submit manuscript

Abstract

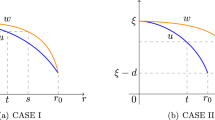
We consider the behaviour of holomorphic functions on a bounded open subset of the plane, satisfying a Lipschitz condition with exponent \(\alpha \), with \(0<\alpha <1\), in the vicinity of an exceptional boundary point where all such functions exhibit some kind of smoothness. Specifically, we consider the relation between the abstract idea of a bounded point derivation on the algebra of such functions and the classical complex derivative evaluated as a limit of difference quotients. We obtain a result which applies, for example, when the open set admits an interior cone at the special boundary point.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Dolzhenko, E.P.: On removal of singularities of analytic functions. Uspehi Mat. Nauk 18, no. 4 (112), 135–42 (1963) [English transl., AMS Translations (2) 97 (1971) 33–41]

  2. Federer, H.: Geometric Measure Theory. Springer, Berlin (1969)

  3. Hormander, L.: The Analysis of Linear Partial Differential Operators I. Springer, New York (1983)

  4. Lord, D., O’Farrell, A.G.: J. d’Analyse Math. (Jerusalem) 63, 103–19 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  5. O’Farrell, A.G.: Equiconvergence of Derivations. Pac. J. Math. 53, 539–554 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  6. O’Farrell, A.G.: Annihilators of rational modules. J. Funct. Anal. 19, 373–389 (1975)

    Article  MATH  MathSciNet  Google Scholar 

  7. Schwartz, L.: Théorie des distributions, 2nd edn. Hermann, Paris (1966)

    MATH  Google Scholar 

  8. Sherbert, D.R.: The structure of ideals and point derivations in Banach algebras of Lipschitz functions. Trans. AMS 111, 240–272 (1964)

    Article  MATH  MathSciNet  Google Scholar 

  9. Zalcman, L.: Null sets for a class of analytic functions. Am. Math. Mon. 75, 462–470 (1968)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematics and Statistics, NUI, Maynooth, Maynooth, Co.Kildare, Ireland

    Anthony G. O’Farrell

Authors
  1. Anthony G. O’Farrell
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anthony G. O’Farrell.

Additional information

Dedicated to Lawrence Zalcman on the occasion of his $$70$$ 70 th birthday.

Rights and permissions

Reprints and permissions

About this article

Cite this article

O’Farrell, A.G. Boundary smoothness of analytic functions. Anal.Math.Phys. 4, 131–144 (2014). https://doi.org/10.1007/s13324-014-0074-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13324-014-0074-0

Keywords

Mathematics Subject Classification (2000)

Search

Navigation