Skip to main content
SpringerLink
Log in

Formulas for Stress Concentration Factors in T&Y Steel Tubular Joints Stiffened with FRP under Bending Moments

  • Published:
International Journal of Steel Structures Aims and scope Submit manuscript

Abstract

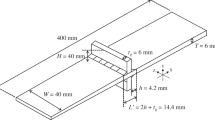
Stress concentration factors (SCF) of steel tubular T/Y-joints strengthened with different types of fiber reinforces polymer (FRP) materials were studied thoroughly under the action of in-plane bending (IPB) and out-of-plane bending (OPB) moments. A comprehensive FE study was carried out through examining different elements for steel substrate and FRP material along with the corresponding contact modeling to attain reliable results substantiated by existing SCF experiments. Shell-to-Solid contact using the node-sharing technique showed the best performance in conformity with the SCF experimental results. Such benchmark modeling was substantiated with additional verifications against the available experimental data on SCFs in T, Y, and K connections. Numerous FE models were then developed to put the most affecting FRP and joint parameters into perspective, while previous studies lack addressing all in one go. It was found that the geometry of the connection has a significant influence on the level of FRP effectiveness. For instance, the sensitivity of SCF in a Y-joint to FRP strengthening is less than a T-joint with similar geometry, due to the different brace-to-chord angles. Justified with analytical interpretations, cumulative effects of all parameters were carefully evaluated to derive SCF formulas for FRP strengthened tubular T/Y-joints under both IPB and OPB moments. Their accuracy and applicability were checked with the well-known statistical indices, and it was seen that the correlation of coefficients was higher than 95%. Moreover, the proposed SCF formulas meet all the acceptance criteria of the Fatigue Guidance Review Panel.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27

Similar content being viewed by others

Abbreviations

D :

Chord outside diameter (mm)

d :

Brace outside diameter (mm)

T:

Chord wall thickness (mm)

t :

Brace wall thickness (mm)

L:

Chord length (mm)

l :

Brace length (mm)

α :

Chord length parameter = 2L/D (–)

β :

Diameter ratio = d/D (–)

γ:

Chord thickness ratio = D/2T (–)

τ :

Wall thickness ratio = t/T (–)

θ :

Brace inclination angle with respect to chord for Y-joints (°)

E 11 :

Longitudinal modulus of elasticity of FRP (GPa)

E 22 :

Transverse modulus of elasticity of FRP (GPa)

ν 12 :

Poisson’s ratio of FRP (–)

G 12 :

Shear modulus along the first and second principal directions of FRP (GPa)

G 13 :

Shear modulus along the first and third principal directions of FRP (GPa)

G 23 :

Shear modulus along the second and third principal directions of FRP (GPa)

SCFs :

Stress concentration factor of FRP-strengthened joint (–)

SCFu :

Stress concentration factor of unstrengthened joint (–)

E s :

Steel modulus of elasticity (GPa)

ν s :

Steel Poisson’s ratio (–)

E p :

Putty modulus of elasticity (GPa)

ν p :

Putty Poisson’s ratio (–)

θ f :

General term which stands for FRP fibers orientation (°)

θ C :

Chord FRP fibers orientation (°)

θ B :

Brace FRP fibers orientation (°)

\(\overline{\theta }\) :

Equivalent FRP fibers orientation (°)

L f :

FRP length on chord (–)

l f :

FRP length on brace (–)

η C :

Chord FRP thickness ratio = thickness of FRP/T (–)

η B :

Brace FRP thickness ratio = thickness of FRP/t (–)

ξ :

Ratio of elasticity modulus of FRP to that of steel = E11/Es (–)

M :

Moment magnitude on the brace (N.m)

σ per :

Geometrical stress in the direction perpendicular to the weld toe (MPa)

σ w :

Geometrical stress at the weld toe (MPa)

σ n :

Nominal stress at brace (MPa)

σ x :

Normal stress component (x direction) (MPa)

σ y :

Normal stress component (y direction) (MPa)

σ z :

Normal stress component (z direction) (MPa)

τ xy :

Shear stress component (xy plane) (MPa)

τ yz :

Shear stress component (yz plane) (MPa)

τ xz :

Shear stress component (xz plane) (MPa)

l 1 :

x-Component of the stress conversion matrix (–)

m 1 :

y-Component of the stress conversion matrix (–)

n 1 :

z-Component of the stress conversion matrix (–)

x n :

x-Component of stress extraction point on the joint in Cartesian coordinates (mm)

y n :

y-Component of stress extraction point on the joint in Cartesian coordinates (mm)

z n :

z-Component of stress extraction point on the joint in Cartesian coordinates (mm)

x w :

x-Component of the weld toe point on the joint in Cartesian coordinates (mm)

y w :

y-Component of the weld toe point on the joint in Cartesian coordinates (mm)

z w :

z-Component of the weld toe point on the joint in Cartesian coordinates (mm)

Δ:

Three-dimensional distance between stress extraction point and weld toe point (mm)

References

  • ABAQUS/Standard User’s Manual. (2014). Version 6.14. Providence. Simulia.

  • Aguilera, J., & Fam, A. (2013). Retrofitting tubular steel T-joints subjected to axial compression in chord and brace members using bonded FRP plates or through-wall steel bolts. Engineering Structures, 48, 602–610.

    Article  Google Scholar 

  • API (American Petroleum Institute). (2014). Recommended practice for planning, designing and constructing fixed offshore platforms—Working stress design, API RP 2A WSD, 22nd edn.

  • AWS (American Welding Society). (2010). Structural welding code, AWS D 1.1:2010 (22nd ed.). Miami: Welding Society Inc.

    Google Scholar 

  • Bao, S., Wang, W., Chai, Y. H., & Li, X. (2020). Hot spot stress parametric equations for three-planar tubular Y-joints subject to in-plane bending moment. Thin-Walled Structures, 149, 106648. https://doi.org/10.1016/j.tws.2020.106648

    Article  Google Scholar 

  • Chang, E., & Dover, W. D. (1996). Stress concentration factor parametric equations for tubular X and DT joints. International Journal of Fatigue, 18(6), 363–387. https://doi.org/10.1016/0142-1123(96)00017-5

    Article  Google Scholar 

  • Chang, E., & Dover, W. D. (1999). Prediction of stress distributions along the intersection of tubular Y and T-joints. International Journal of Fatigue, 21(4), 361–381. https://doi.org/10.1016/S0142-1123(98)00083-8

    Article  Google Scholar 

  • Efthymiou, M. (1988). Development of SCF formulae and generalised influence functions for use in fatigue analysis. In Proceedings of the conference on recent developments in tubular joints technology (pp. 1–13).

  • Fatigue Guidance Review Panel—MaTSU. (1996). Fatigue background guidance document. In HSE books as a offshore technology report.

  • Fu, Y., Tong, L., He, L., & Zhao, X.-L. (2016). Experimental and numerical investigation on behavior of CFRP-strengthened circular hollow section gap K-joints. Thin-Walled Structures, 102, 80–97. https://doi.org/10.1016/j.tws.2016.01.020

    Article  Google Scholar 

  • Hectors, K., & De Waele, W. (2021). Influence of weld geometry on stress concentration factor distributions in tubular joints. Journal of Constructional Steel Research, 176, 106376. https://doi.org/10.1016/j.jcsr.2020.106376

    Article  Google Scholar 

  • Hellier, A. K., Connolly, M. P., & Dover, W. D. (1990). Stress concentration factors for tubular Y- and T-joints. International Journal of Fatigue, 12(1), 13–23. https://doi.org/10.1016/0142-1123(90)90338-F

    Article  Google Scholar 

  • Hosseini, A. S., Bahaari, M. R., & Lesani, M. (2019). Parametric study of FRP strengthening on stress concentration factors in an offshore tubular T-joint subjected to in-plane and out-of-plane bending moments. International Journal of Steel Structures, 19(6), 1755–1766.

    Article  Google Scholar 

  • Hosseini, A. S., Bahaari, M. R., & Lesani, M. (2020). Experimental and parametric studies of SCFs in FRP strengthened tubular T-joints under axially loaded brace. Engineering Structures, 213, 110548.

    Article  Google Scholar 

  • IIW-XV-E. (1999). Recommended fatigue design procedure for welded hollow section joints. Paris: International Institute of Welding Paris.

    Google Scholar 

  • Lesani, M., Bahaari, M. R., & Shokrieh, M. M. (2014). Experimental investigation of FRP-strengthened tubular T-joints under axial compressive loads. Construction and Building Materials, 53, 243–252. https://doi.org/10.1016/j.conbuildmat.2013.11.097

    Article  Google Scholar 

  • Lloyd’s Register of Shipping. (1997). UK health and safety executive. OTH 354: stress concentration factors for simple tubular joints—Assessment of existing and development of new parametric formulae. London, UK.

  • Morgan, M. R., & Lee, M. M. (1998). Parametric equations for distributions of stress concentration factors in tubular K-joints under out-of-plane moment loading. International Journal of Fatigue, 20(6), 449–461. https://doi.org/10.1016/S0142-1123(98)00011-5

    Article  Google Scholar 

  • Nassiraei, H., & Rezadoost, P. (2021). Stress concentration factors in tubular T/Y-connections reinforced with FRP under in-plane bending load. Marine Structures, 76, 102871.

    Article  Google Scholar 

  • N’Diaye, A., Hariri, S., Pluvinage, G., & Azari, Z. (2007). Stress concentration factor analysis for notched welded tubular T-joints. International Journal of Fatigue, 29(8), 1554–1570. https://doi.org/10.1016/j.ijfatigue.2006.10.030

    Article  Google Scholar 

  • Potvin, A. B., Kuang, J. G., Leick, R. D., & Kahlich, J. L. (1977). Stress concentration in tubular joints. Society of Petroleum Engineers Journal, 17(04), 287–299.

    Article  Google Scholar 

  • Sadat Hosseini, A., Bahaari, M. R., & Lesani, M. (2019). Stress concentration factors in FRP-strengthened offshore steel tubular T-joints under various brace loadings. Structures. https://doi.org/10.1016/j.istruc.2019.07.004

    Article  Google Scholar 

  • Sadat Hosseini, A., Bahaari, M. R., Lesani, M., & Hajikarimi, P. (2021a). Static load-bearing capacity formulation for steel tubular T/Y-joints strengthened with GFRP and CFRP. Composite Structures, 268, 113950. https://doi.org/10.1016/j.compstruct.2021.113950

    Article  Google Scholar 

  • Sadat Hosseini, A., Zavvar, E., & Ahmadi, H. (2021b). Stress concentration factors in FRP-strengthened steel tubular KT-joints. Applied Ocean Research, 108, 102525. https://doi.org/10.1016/j.apor.2021.102525

    Article  Google Scholar 

  • Standards Norway. (2004). NORSOK: N-004: Design of steel structures. The Norwegian Oil Industry Association (OLF) and Federation of Norwegian Manufacturing Industries.

  • Teng, J. G., Yu, T., & Fernando, D. (2012). Strengthening of steel structures with fiber-reinforced polymer composites. Journal of Constructional Steel Research, 78, 131–143. https://doi.org/10.1016/j.jcsr.2012.06.011

    Article  Google Scholar 

  • Tong, L., Xu, G., Zhao, X.-L., Zhou, H., & Xu, F. (2019). Experimental and theoretical studies on reducing hot spot stress on CHS gap K-joints with CFRP strengthening. Engineering Structures, 201, 109827. https://doi.org/10.1016/j.engstruct.2019.109827

    Article  Google Scholar 

  • Xu, G., Tong, L., Zhao, X.-L., Zhou, H., & Xu, F. (2020). Numerical analysis and formulae for SCF reduction coefficients of CFRP-strengthened CHS gap K-joints. Engineering Structures, 210, 110369. https://doi.org/10.1016/j.engstruct.2020.110369

    Article  Google Scholar 

  • Zhao, X. L., Herion, S., Packer, J. A., Puthli, R. S., Sedlacek, G., Wardenier, J. (2001). CIDECT: Design guide for circular and rectangular hollow section joints under fatigue loading. In CIDECT, Comité. International pour le développement et l'etude de la. construction tubulaire.

Download references

Funding

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Author information

Authors and Affiliations

  1. School of Civil Engineering, College of Engineering, University of Tehran, Tehran, Iran

    Alireza Sadat Hosseini & Mohammad Reza Bahaari

  2. School of Civil Engineering, Sadra Institute of Higher Education, Tehran, Iran

    Mohammad Lesani

Authors
  1. Alireza Sadat Hosseini
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammad Reza Bahaari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Lesani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohammad Reza Bahaari.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sadat Hosseini, A., Bahaari, M.R. & Lesani, M. Formulas for Stress Concentration Factors in T&Y Steel Tubular Joints Stiffened with FRP under Bending Moments. Int J Steel Struct 22, 1408–1432 (2022). https://doi.org/10.1007/s13296-022-00651-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13296-022-00651-w

Keywords

Search

Navigation