Network structures of urban ride-pooling problems and their properties

Abstract

Travellers, when sharing their rides in a so-called ride-pooling system, form complex networks. Despite being the algorithmic backbone to the ride-pooling problems, the shareability graphs have not been explicitly analysed yet. Here, we formalise them, study their properties and analyse relations between topological properties and expected ride-pooling performance. We introduce and formalise two representations at the two crucial stages of pooling analysis. On the NYC dataset, we run two simulations with the link generation formulas. One is when we increase discount offered to the travellers for shared rides (our control variable) and observe the phase transition. In the second, we replicate the non-deterministic behaviour of travellers in ride-pooling. This way, we generate probabilistic, weighted networks. We observed a strong correlation between the topological properties of ride-pooling networks and the system performance. Introduced class of networks paves the road to applying the network science methods to a variety of ride-pooling problems, like virus spreading, optimal pricing or stability analysis.

1 Introduction

An increasingly popular urban mobility alternative is ride-pooling, where travellers share a vehicle to reach their destination, as illustrated in Fig. 1. By pooling, travellers can reduce their travel costs (thanks to discounted fare), mobility platforms (like Uber and Lyft) can use their fleets more efficiently, and cities can reduce emissions (via reduce mileage). As identified in the seminal work of Santi et al. (2014) and Alonso-Mora et al. (2017), travellers who decide to share their trips form graph structures. Although the so-called shareability networks are central to solving the challenging ride-pooling problems, hitherto they have not been explicitly analysed.

Fig. 1

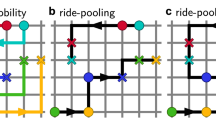
Ride-pooling illustrated. Three travellers request to travel from their origins (marked with $\times$) to destinations (marked with a $\nabla$). Apart from offering them three separate solo rides (marked with grey), ride-hailing platform (like Uber) offers to pool them together and serve with a single trip (red). Such pooled ride can be expressed as a network, where nodes are travellers, linked when they travel together. As we demonstrate, several meaningful network representations can arise (Color figure online)

From a network perspective, ride-pooling can be seen as the connection between two or more nodes. The node is a traveller, or more precisely, her trip request (her origin, destination and request time). The link is established on two levels. First, when travellers agree to travel together (in our case, this means that the shared trip is attractive to all co-travellers). Second, when they actually travel together (when each traveller is uniquely assigned to a particular trip).

These two interpretations of the links lead to two different network structures (the second being a subgraph of the first). We will refer to the first representation as shareability, i.e. the potential to travel together, and the second as matching, i.e. actual travel together. In the former, the link generation is on one side driven by the spatio-temporal similarity of pooled trips (trips from nearby origins to nearby destinations, close temporary) and on the other, by the behaviour (travellers’ willingness-to-share and value-of-time). Shareability between two travellers is asymmetrical, i.e. it may be attractive for me to travel with you, yet it is not necessarily attractive for you to travel with me. Here, we assume that the link is formed only when the attractiveness is bidirectional (making the graph undirected). While an individual can be the part of multiple pooled rides, she can travel only with one selected ride. Represented as the matching, a sub-graph of the shareability and the links that remain are part of the optimal solution such that each traveller is uniquely assigned to a ride and the total cost of rides is minimised (typically total distance or time).

Such network representation, despite being meaningful, is ambiguous. For instance, three pairwise connected travellers form a triangle on the shareability graph, yet we cannot tell if they can form a triple and travel together, or not. To this end, we propose an alternative, bipartite formulation. We introduce a new type of node: the trip, which can be interpreted as a vehicle trip during which co-travellers travel together. In the bipartite network, the links are formed between travellers and rides. We will refer to the former as simple networks and the latter as bipartite networks.

These two levels of twofold distinction lead to four types of networks, which we explore in this paper. We run two simulations to understand the significance of those networks. To understand how the network properties evolve with the control variable, we gradually increase the discount offered for pooled rides. This directly impacts the link generation formula in the shareability network, since the travellers’ willingness to ride together is incentivised at lower costs. We not only observe the transition, but also their strong correlations with ride-pooling system performance indicators. Then, we explore the stability of networks and their properties with non-deterministic ride-pooling behaviour. In that case, the link generation depends on non-deterministic willingness-to-share between two travellers. In reality, despite the spatio-temporal similarity of trips, the travellers may be unwilling to share (due to their behavioural traits), or vice versa wanting to share despite high detours and delays. We incorporate such a notion (using recent empirical findings on heterogeneous ride-pooling behaviour) and generate the probabilistic, weighted version of the shareability graphs.

Such weighted shareability and matching graphs, consistent with the actual travel behaviour, can be useful not only for a deeper understand of the still challenging ride-pooling problems, but also instrumental in the variety of practical problems with established network-science techniques, like: community detection, discriminative pricing, vital nodes or virus spreading in ride-pooling networks.

1.1 Related literature

Shareability networks were introduced in ride-pooling by Santi et al. (2014), who used networks to translate spatio-temporal problems into a graph framework. The graph representation was simplified by the algorithm constraint, which allowed matching at most two travellers (here we allow any ride degree). The network representation was further extended by Alonso-Mora et al. (2017) allowing for higher degree trips. In their study, nodes were both travellers and vehicles linked when they were travelling together (similar to our bipartite networks).

Many authors have proposed real-time algorithms to solve the ride-pooling problem. Most of them rely on fixed time or distance windows (Santi et al. 2014; Ke et al. 2021; Shah et al. 2020; Bilali et al. 2020; Wang et al. 2021). Pooling passengers are governed with the hard constraints, i.e. when the delay and detour are within the given bounds travellers are pooled, which can be seen as a link generation formula of the underlying network. In our study, we use the ExMAS algorithm proposed by Kucharski and Cats (2020). It is an off-line method applied from the perspective of the traveller; it uses the behavioural utility-based link generation formula and allows finding an exact solution for real-size ride-pooling problems.

Recent studies reported that attitude towards pooling varies among heterogeneous individuals (Krueger et al. 2016; Lavieri and Bhat 2019; Alonso-González et al. 2020). Ranging from with pooling enthusiasts, who prefer shared rides due to environmental benefits, up to sceptics who are time-sensitive and unwilling to travel in a crowded vehicle (Alonso-González et al. 2020). Such an approach makes the link generation formula probabilistic, dependent on the latent behaviour of individual travellers. To estimate the probabilities of links and nodes, we introduce weighted ride-pooling networks, which often represent reality better than their unweighted counterparts (e.g. Squartini et al. 2011; Aftabuddin and Kundu 2006; De Montis et al. 2007). We introduce the probabilistic part in the utility formula, remaining consistent with discrete choice theory Ortúzar and Willumsen (2011).

Introducing the class of network structures within the formulation of ride pooling problem should allow for the application of a wide spectrum of complex networks techniques. The exemplary applications are: studies on virus spreading mitigation while maintaining the service effectiveness (Zareie and Sakellariou 2022); social network interventions which consider topological relationships existing between communities (Corcoran et al. 2022); day-to-day virus spreading via pooling system (Kucharski et al. 2021); multi-objective optimisation to identify key players in large social networks which can be applied to find crucial travellers for the service performance (Gunasekara et al. 2015).

The network structures introduced by Santi et al. (2014) and Alonso-Mora et al. (2017) were used in the algorithms, but not explicitly analysed. In our study, we formalise simple and bipartite representation. We tried to quantify the networks with a standard measures; however, certain properties, such as the clustering coefficient [introduced in Watts and Strogatz (1998)], cannot be calculated in the usual way for the bipartite network, as recognised by Lind et al. (2005). Hence, we use the approach proposed by Zhang et al. (2008).

In this study, we reveal the potential of ride-pooling networks towards better understanding the challenges of ride-pooling. We formalise the networks and experimentally show not only that they well approximate the key performance indicators of ride-pooling, but also provide rich meaningful structures, instrumental for a series of opened ride-pooling problems.

2 Methodology

We start with a brief introduction of the ride-pooling algorithm that we use to generate our networks. We focus on the link generation formula, which governs creating the shareability networks. Then, we formalise the four network structures that emerge while solving the ride-pooling problem. We introduce the network measures that we find meaningful to observe in our simulations. We consider two versions of the link-generation formula: deterministic and probabilistic. Thus, in the last stage, we formalise the probabilistic link-generation formula and the resulting estimates of probabilistic networks.

2.1 Ride-pooling algorithm

Exact matching of attractive shared rides (ExMAS) is a utility-based algorithm introduced by Kucharski and Cats (2020). It is an offline algorithm that allows finding an optimal solution to the ride-pooling problem. Unlike many real-time algorithms, the traveller is placed in the middle. We do not assume any hard constraints (time window, detour length), but we compute whether the trip is attractive to the user. To assess whether a shared ride is attractive to the traveller, we compare its perceived utility with the utility of a private ride by applying the formulas:

$$\begin{aligned} \begin{aligned}&U^{ns}_i = \beta _c \lambda l_i + \beta _t t_i \\&U^s_{i, r_k} = \beta _c (1 - \lambda _s)\lambda l_i + \beta _t \beta _s ({\hat{t}}_i + \beta _d {\hat{t}}^p_i) + \varepsilon , \end{aligned} \end{aligned}$$

(1)

where $U^s_{i, r_k}$, $U^{ns}_i$ denote, respectively, utility of shared ride (for i-th traveller, ride $r_k$) and utility of non-shared ride (for i-th traveller). $\lambda$ stands for price, while $\lambda _s$ denotes discount for sharing a ride. Both are controlled by the operator, yet in the simulations we play only with the discount. $\beta ^c$, $\beta ^t$, $\beta ^s$ $\beta ^d$ are the exogenous behavioural parameters: cost sensitivity, value of time, sharing discomfort and delay sensitivity, respectively. $t_i$ and ${\hat{t}}_i$ stand for travel time of non-shared and shared ride, respectively, ${\hat{t}}^p_i$ is a pick-up delay associated with pooling and $\varepsilon$ is a random term.

Utility formulas determine the sign of the difference $U^s_{i, r_k} - U^{ns}_i$. In the simulation process, in each run, we sample the random term (epsilon) hence obtaining a specific utility value for each ride for each traveller. If the sign is positive, we say that the ride is attractive for the traveller. If a ride is attractive for all its participants, we say that the ride is feasible. Notably, from our network’s perspective, the utility-formula can be interpreted as the link generation formula in the shareability graph. We assume that the only endogenous variable is the price and discount ($\lambda$’s controlled by the platform provider) and other components are exogenous and not directly controlled, including the behavioural traits $\beta$s, random term $\varepsilon$ and detour ${\hat{t}}_i$ and delay ${\hat{t}}^p_i$ (which depend on the particular ride realisation—as illustrated in Fig. 1).

ExMAS first determines the set of feasible rides. The ride is defined as any subset of travellers’ trips (including a solo ride) with the specific order of pick-ups and drop-offs of co-travellers. We start by assuming that a private trip is always feasible for the traveller. Next, we determine the set of pairs (rides comprising two travellers), which already creates the shareability graph [which, in the original ExMAS algorithm, is a directed-multigraph (Kucharski and Cats 2020)]. From the rides in the pair-wise shareability graph, we gradually search for rides of higher degree. Potential rides of higher degree are identified as cliques and searched recursively. Feasible triples are composed of feasible pairs, quadruple of triples and so on. This approach allows us to reduce the search space, and the proposed algorithm remains exhaustive. (All attractive rides are found.)

From the set of all feasible pooled rides, we find the optimal subset that maximises our objective function. Notably, the matching is done by the operator. Travellers are already satisfied with the potential assignments as the set of the feasible rides comprises only attractive rides and the operator is free to identify the optimal matching within the attractive rides. In the study, the objective is the total mileage (distance travelled). By solving the bipartite matching problem, we find the optimal subset that satisfies the condition that each traveller is served exactly with a single ride. The final solution is the set of rides which is referred to as matching.¹

2.2 Shareability networks

The shareability graphs emerging while solving ride-pooling problems were introduced already in the seminal paper by Santi et al. (2014). Here, we formalise it in more detail. The first representation (further denoted as a simple) is a network where nodes represent travellers and links represent feasible rides. Two nodes are connected if a trip comprising the two travellers is attractive to both of them. The network is easy to interpret, but the underlying information is ambiguous. For example, if three nodes form a triangle, we do not know whether the whole triple constitutes a feasible ride of third degree, or just all of three connected pairs are feasible. To avoid this ambiguity, we propose an alternative representation. We construct a bipartite network where nodes are formed not only with travellers but also with feasible rides. Travellers are connected to all feasible trips in which they participate. Ride is connected with all the travellers that participate in it.

Both formulations of the shareability graph, despite meaningful, are unfeasible in practice. Namely, each traveller may be part of multiple feasible rides, while in practice she can travel only in one of them. The physical implementation of ride pooling is a matching graph, which contains only links being part of the optimal matching. The constraint on bipartite matching is that each traveller is uniquely assigned to exactly one ride, and the objective is to minimise the total mileage. The optimal matching can be formed as a subset of both a simple and bipartite network. The resulting four types of networks are summarised in Table 1 and visualised for the case study of 147 NYC trip requests in Fig. 2.

Table 1 Four networks of ride pooling. Simple and bipartite representations at the two levels: all the feasible rides (shareability) and the optimal solution (matching)

Fig. 2

Four representations of networks of the ride-pooling problem solved for the case of 147 pooling travellers in NYC (detailed in the results). The shareability network (a) is highly connected, many nodes (travellers) are linked with multiple other potential co-travellers. However, when travellers are uniquely assigned to vehicles in the matching network (b) the structure becomes dramatically more sparse. The bipartite forms of those two networks have similar structures. Travellers (top) are linked with rides (bottom). Among multiple potentially feasible links (c), only a few remain the part of actual matching (d). For illustration, we highlighted a single traveller with red for all the structures. One sample traveller can share a ride with 10 other travellers (a); in 23 different shared rides and a single solo ride (c). She is matched to the ride of degree 3 (b) which is uniquely represented in the lower side of the bipartite matching network (d)

Mind that while the utility formulas in Eq. 1 can be seen as the link generation formula for the graphs, it is not straightforward. In the simple shareability network, the link between nodes i and j is formed if and only if both i and j opt to participate in a shared ride. As the utility formula determines the feasibility of rides, in the bipartite matching network, Eq. 1 conditions the existence of (rides) nodes among which the optimal matching is selected. Matching structures are subsets of the shareability counterparts (hence indirectly impacted by the utility formula); however, the subsetting process is subject to objective maximisation (mileage reduction) and irrespective of the utility values. Nonetheless, while we do not derive an explicit link generation formula, the utility equations remain the main driver of the ride-pooling networks’ structures.

2.3 Topological measures

We measure topologies of the networks with the following set of state-of-the-practice indicators. We selected meaningful and interpretable indicators which were either correlated with performance indicators or evolved nicely along the transition of the system.

We start with average node degrees (the averaged number of connections that a node has to other nodes in the network), reported in three forms: for travellers in the simple networks, for travellers and for rides in the bipartite networks. Average degree in simple shareability network represents the number of feasible rides one passenger has. In the simple matching graph, the average degree represents the number of assigned co-travellers. In bipartite representation, the degree of traveller node denotes the number of feasible rides in the shareability network and is, by the definition, always equal to 1 in the matching network. Degree of the ride node is the number of travellers participating in the ride.

For both networks, we report the coverage of the largest component, i.e. the fraction of nodes that forms the largest connected subnetwork. Formally, given the graph with n nodes, we find its largest connected component, which has m nodes ($m <= n$). Hence, we define coverage of the largest component as the fraction m/n. While the relative size (coverage) of the largest component has no direct physical interpretation, it demonstrates network connectivity and the values significantly differ between the simple and bipartite network representations.

To understand how many travellers cannot share any ride, we compute either number of isolate nodes (node of degree 0 in the simple graphs) or the number of isolated links (pair traveller-ride in the bipartite networks, where both nodes are of degree 1).

Finally, we report various forms of clustering coefficients. We define clustering coefficient $c_v$ of a node v as

$$\begin{aligned} c_v = \frac{2T(v)}{\deg (v)(\deg (v) - 1)}, \end{aligned}$$

(2)

where T(v) denotes number of triangles through the node v, and $\deg (v)$ is the degree of the node v. For the simple network the classic method is applicable, yet not for the bipartite network. Therefore, we use the formula suggested by Zhang et al. (2008):

$$\begin{aligned} C_4(v) = \frac{\sum _{u=1}^{k_v} \sum _{w=u+1}^{k_v} q_v(u,w)}{\sum _{u=1}^{k_v} \sum _{w=u+1}^{k_v} [a_v(u,w) + q_v(u,w)]}, \end{aligned}$$

(3)

where $C_4(v)$ is the square clustering of the node v, $k_v$ is its degree, $q_v(u,w)$ is the number of common neighbours of u and w, $a_v(u,w) = k_u - (1+q_v(u,w)+\theta _{uv}) + k_w - (1+q_v(u,w)+\theta _{u,w})$, where $\theta _{u,w}$ is a binary variable indicating whether u and w are connected. We report average clustering coefficients for two sides of nodes in bipartite networks of nodes: travellers and rides. We also distinguish between nodes corresponding to shared rides (or travellers who can share) and solo rides (or travellers who are restricted to private rides only). Clustering coefficient of a node in the simple network represents a probability that two neighbours of the node are connected. Square clustering coefficient of a node in the bipartite network denotes probability that for the two neighbours of the node, there is another common neighbour.

2.4 Non-deterministic link generation formula

Despite the random term $\varepsilon$ in the link generation formula (Eq. 1), we hitherto assumed the resulting networks are deterministic ($\varepsilon =0$). Yet, recent empirical findings Alonso-González et al. (2020) suggest that attitudes towards pooling vary across the population. To account for the fact, we have adopted a probabilistic model with utility composed of two parts: deterministic and the random term $\varepsilon$ following the normal distribution. The formulation yields the so-called probit model [detailed, e.g. in Ortúzar and Willumsen (2011)]. Determining whether a traveller accepts a shared ride (and forms a link in the shareability network) is now probabilistic. According to the probit formulation, we can say that the probability that the traveller i chooses to participate in the shared ride $r_j$ is given by:

$$\begin{aligned} {\textbf{P}}(t_i \in r_j)= \, & {} {\textbf{P}}(U^s_{i, r_j} - U^{ns}_i> 0) = {\textbf{P}}({\hat{U}}^s_{i, r_j} + \varepsilon - U^{ns}_i> 0) \nonumber \\= \, & {} {\textbf{P}}({\hat{U}}^s_{i, r_j} - U^{ns}_i > -\varepsilon ) = \Phi _{0, \sigma }({\hat{U}}^s_{i, r_j} - U^{ns}_i), \end{aligned}$$

(4)

where $\Phi _{0, \sigma }$ is the cumulative distribution function (CDF) of the normal distribution with mean 0 and standard deviation $\sigma$ and ${\hat{U}}^s_{i, r_j}$ is the deterministic part of $U^s_{i, r_j}$.

For the simulation purposes, from the formulation ${\textbf{P}}({\hat{U}}^s_{i, r_j} - U^{ns}_i > -\varepsilon )$ in Eq. 4 and symmetry of $\varepsilon$ in 0, we can notice that the problem is equivalent to setting a normally distributed threshold $T_i$ such that, if for deterministic ${\hat{U}}^s_{i, r_j}$, ${\hat{U}}^s_{i, r_j} - U^{ns}_i > T_i$, the ride $r_j$ is attractive to the i-th traveller. We assume the traveller has a consistent attitude. It means that the threshold $T_i$ is fixed for the i-th traveller in a single replication of the random process.

2.5 Non-deterministic shareability networks

Introducing the random element into the utility formula (Eq. 1) enriches the underlying network structures. In general, the networks become probabilistic and those described in Sect. 2.2 are barely a single realisation of the random process. With the probabilistic nature of the link-generating formula, we can propose a new representation of ride-pooling networks.

Unfortunately, the analytic derivation of probabilistic networks is impossible, since long tails of normal distribution will make the shareability networks complete (each ride has a positive probability of being feasible, no matter how small). While adopting a probabilistic model to pairwise shareability may still remain feasible for practical problems, it becomes impossible for greater degrees. We would have to consider the power set of travellers, as well as the permutation of the order of pick-ups from origins and the permutation of the order of drop-offs at destinations (Fielbaum et al. 2022). Enumerating all the potential rides and finding the optimal (probabilistic) solution in such space is computationally unfeasible.

Thus, we resort to reproducing the networks experimentally, via replications. We replicate the sampling to obtain a sufficient number of realisations of the variables and in this way approximate the true, probabilistic results. We propose weighted networks, where nodes and links are the union of all nodes and links that appeared in graphs across replications. Each link is assigned a weight reflecting the number of replications in which it occurred and further loosely interpreted as an estimate of its probability.

Network structures vary across replications due to the probabilistic link-generating formula. In the simple networks, the nodes remain intact (travellers and their requests are assumed fixed), yet links are formed probabilistically. For bipartite networks, the traveller nodes do not change compared to deterministic representation, but the set of feasible rides (ride nodes) changes across replications.

3 Results

3.1 Simulation design

We experiment with the dataset of trips actually requested within half an hour in New York City in January 2016.² Each of the 147 requests links an origin with a destination at a given time (illustrated in Fig. 3).

We solve the ride-pooling problem for that demand with ExMAS, specifically we solve the off-line version of the ride-pooling problem (demand is assumed to be known in advance), do not explicitly handle individual vehicles and focus on the shareability between travellers instead. We assumed a realistic parametrisation of utility formula (Eq. 1) with fare $\lambda$ of 1.5 $/km [consistent with NYC Taxi & Limousine Commission (2022)], a sharing discount $\lambda _s$ of $30\%$ [in the range suggested by Shaheen and Cohen (2019)], a time value of $\beta _t=16.56\$/h$, willingness to share $\beta _s=1.148$ [which is the weighted averages of the mean values reported in the empirical study of Alonso-González et al. (2020)] and we set no additional penalty for delay, i.e. $\beta _d = 1$.

We run two simulations for analyses. First when we trace the transition in the shareability graph by increasing the probability in link generation formula (via the discount $\lambda _s$ offered for sharing in Eq. 1) and second when we assume link-generation formula is probabilistic and we replicate the ride-polling problem solutions to obtain weighted probabilistic networks. (Link is generated with a probability given with Eq. 4.)

In the former, we gradually increase the discount from 0 to $50\%$ with the fixed demand structure. In the latter, we assume that $\varepsilon$ in Eq. 1 follows the standard normal distribution (mean of 0, variance of 1) and is once drawn per replication for each traveller. We replicate the sampling 1000 times to obtain a meaningful approximation of link probabilities.

Fig. 3

Demand dataset for simulations: 147 trip requests from Jan 2016 in Manhattan, NYC. Green dots represent origins, orange—destinations (Color figure online)

3.2 Transition via increasing ride-pooling discount

System settings, along with demand structure, determine the topology of the ride-pooling networks. We investigate the relation between the sharing discount and network characteristics. From the traveller’s perspective, sharing discount constitutes the positive side of ride-pooling. The discomfort associated with sharing and the extension of the total travel time (which we do not control) must be sufficiently compensated, with a discount (which we control) in the utility formula (Eq. 1).

Figure 4 demonstrates the impact of the sharing discount on the structure of the shareability graphs and on the efficiency of the system.

Fig. 4

Transition in the graph structures induced by increasing ride-pooling discount. The average node degree of both travellers and rides increases as the network becomes more densely connected with greater discount (Fig. 4a); however, the shapes and values are different, the number of trips to which a traveller can be matched (green) increases exponentially and reaches several hundred feasible rides. The average degree of rides (blue) increases linearly and reaches an average degree of 3.5. Clustering coefficient in the bipartite network starts increasing both for travellers and rides for discounts greater than 20% (Fig. 4b). Figure 4c demonstrates, for the simple network, the average degree (green), which denotes with how many other co-travellers one can share a ride and the average clustering coefficient (blue) denotes the probability that your neighbours are also connected. Figure 4d depicts the impact of the sharing discount on two economical properties: the profitability of the ride-pooling system and the number of rides. The profitability represents how the discounted fares (reduced profits) are compensated with the reduced costs (lower mileage). It is positive when the mileage reduction is greater the fare discount

When no discount is offered, travellers do not share rides, the network composed of isolated nodes. When the discount is high, the number of feasible rides increases sharply, shifting towards a connected regime (when most pairs of travellers would be happy to share a ride). Increasing the sharing discount makes shared rides more attractive and, in the network interpretation, new links appear. In the bipartite structure (Fig. 4a), the degree of a traveller node is the number of different rides he is willing to participate in. The degree of a ride is the number of travellers assigned to it. Hence, the average degree of the ride node is the expected occupancy of a ride. In Fig. 4a, we can see that the $10\%$ discount level marks the critical point. In the subcritical regime, below this level, none of the shared rides is feasible (node degree equal to 1). For discount higher than 10%, complex rides (high degree rides) appear and passengers become more flexible. The space of feasible rides grows rapidly (about 16000 feasible rides for sharing discounts at the level of $50\%$), transitioning the networks towards the supercritical regime. The growth indicates a great increase in computational complexity, as was observed in computation times of ride-pooling problem under high discounts.

We did not observe the fully connected regime, where all nodes are part of the largest component. Some trip pairs remained incompatible regardless of the high discount, since they would require detours and delays which cannot be compensated even with 50% discounts. As we observed, rides which require high discounts to appear in the shareability graphs are rarely part of the optimal solution (matching), as they induce high detours.

Figure 4b demonstrates the distribution of the average square clustering coefficient. The coefficient calculated for shared rides represents the probability that there is an alternative trip for two of its participants. For the traveller, it demonstrates the probability that two of his feasible rides are shared with another passenger (the same co-traveller for both). The square clustering coefficient remains zero when the first trips of the second degree appear. Notably, this measure increases later, only when discount exceeds 15% and reaches 0.13 for travellers and 0.09 for rides.

The topological properties of the simple shareability network are shown in Fig. 4c. Here, the degree is the number of feasible co-travellers and the clustering coefficient is the probability that, for the given node, two of its neighbours can share a ride. For a regular discount of $30\%$, the average node degree is 6.5, while for a discount of $50\%$ it reaches over 20. The clustering coefficient initially grows relatively faster than the degree. Later, the growth of the degree is more pronounced, which could suggest linking between communities. At the maximum discount level, the average probability for a node that two of its neighbours are connected reaches 0.5.

In Fig. 4d, we plot the pooling profitability and the number of rides. For the lowest values of sharing discount ($\le 10\%$), none of the shared rides is feasible. Feasible rides which appear for the low sharing discount (10–20%) are highly profitable. Travellers who jointly recognise such combinations attractive are highly compatible. In the simulation settings, the most profitable system was obtained for the discount at the level of 0.18. As expected, with increasing sharing discount travellers become more flexible and are easier to pool in shared rides (decrease in the number of rides). However, the saved mileage does not sufficiently compensate for the income reduction associated with increased discount, and thus, for high discount levels ($>20\%$), the generated benefits are outbalanced by the reduced profits.

3.3 Shareability graph as a proxy to key performance indicators

Here, we verify if the shareability network properties correlate with ride-pooling performance. In Table 2, we show correlation between network properties and pooling performance obtained for discount levels increasing gradually to 50%. We selected three performance indicators for the ride-pooling system. The operator’s and environmental’s perspective is reported as a reduction in vehicle mileage (lower total distance due to pooling). From the user’s perspective, we measure aggregated satisfaction gain (improved utility of pooling, as in Eq. 1). The last indicator is a fraction of travellers who effectively share a ride in the system (effectiveness). We see how well they correlate with the nine selected network properties, as described in Sect. 2.3.

Table 2 Correlation between topological properties of the bipartite shareability graph and performance indicators of the ride-pooling system. Obtained for gradually increasing discount levels between 0 and 50%. Mileage reduction is best described with average clustering of shared rides, utility gains with average degree of rides and fraction of shared rides with isolated nodes

In most of the cases, the correlation coefficient exceeds 0.9, suggesting a close to linear relation. This is an indication that the topological properties of the shareability graph can be used as a proxy to estimate the pooling performance.

Fig. 5

Relation between topological properties of the bipartite shareability graph (average degree of ride nodes in the first row and average degree of traveller nodes in the second row) and system’s performance indicators (mileage reduction, sharing ratio and utility gain in columns, respectively). Each graph contains 51 points obtained for increasing discounts (marked with colour). Each relation is strong and can be well approximated with linear, exponential or logarithmic trends—which offers a variety of strong predictors (Color figure online)

To further explore the shape of those strong relations, we investigate shapes of the selected regression plots in Fig. 5. The high correlation coefficients shown in Table 2 are expressed in a very clear trend. With linear to logarithmic trend in the subfigures in the first row, where the average degree of ride node represents the mean number of travellers in a feasible ride and three respective ride-pooling indicators are shown in the columns. The mean value of the traveller node degree in the second row informs how many feasible assignments one traveller has on average. We see the values grow strongly in the beginning. Later, however, the trend becomes weaker. Above a certain discount level, travellers are willing to share a trip under very unfavourable conditions, which are usually also not attractive from the perspective of mileage reduction. As a result, additional feasible trips are often discarded at the matching stage, which well explains the non-linearities in the second row of Fig. 2.

3.4 Variability introduced by the random term

In the second simulation, we want to understand stability of the shareability networks under fixed settings, yet with the probabilistic link generation formula. We assume the random term $\varepsilon$ in Eq. 1 is normally distributed and replicate the ride-pooling problem 1000 times for the same demand set.

We first look at the properties of the ride-pooling networks and their stability across replications in Table 3. Some properties of the networks remain constant by definition. For example, the number of nodes in the simple networks is equal to the number of travellers. Similarly, the number of links in bipartite matching. However, examining different structural properties reveals interesting patterns.

Table 3 General properties and their variability in 1000 replications (standard deviation in brackets) for the four introduced graph structures

For the simple networks, we can see that there is a significant deviation in the number of edges in the shareability graph. This finding highlights the significance of the random term at the early stage of the pooling algorithm (finding feasible pairs). The matching networks (mirroring the pooling realisation) are significantly less variable and much more stable. The matching network results from the optimisation, which is deterministic; thus, the random link generation has a limited impact. The matching changes only when the link being part of the optimal solution is not generated. The average degree of the traveller node in the bipartite shareability network, corresponding to the number of feasible trips, has a notable deviation. It highlights the significance of the random term in finding feasible rides of a higher degree.

For better understanding of this random process, let us consider the two tails of the underlying process: favourable (when travellers are willing to share) and unfavourable (the opposite). Under unfavourable pooling conditions, travellers either travel alone or match into rides of low degree. However, connectivity in the simple network can already reach high levels as it is based only on pairwise relation. Rides of degree three and higher do not impact the shareability graph structure. Conversely, the major part of the bipartite network corresponds to complex, high degree rides. Hence, the size of the largest component greater in the bipartite network than in the simple network indicates that there are many complex rides present within the largest component.

3.5 Weighted shareability networks

Probabilistic approach gives a rise to more complex network structures. We visualise the weighted graphs as the generalisation of their deterministic counterparts, in Fig. 6. The weight of the link (thickness) is an indicator of its probability. Highly probable links can be interpreted as stable matches, such links are present even if the sampled attitude towards pooling ($\varepsilon$) is unfavourable. Low weight links represent trips that only occur in favourable outcome of the probabilistic process, when their participants are pooling enthusiasts.

Figure 6 demonstrates the proposed four weighted network structures. Shareability networks (Fig. 6a, c) aggregate feasible connections from all replications, while matching networks (Fig. 6b, d) physical realisations. Simple networks (Fig. 6a, b) allow to easily asses travellers’ compatibility and network density, while bipartite networks (Fig. 6c, d) reveal complete information, which becomes illegible for such dense network wirings.

Weighted network structures allow us to investigate connectiveness and stability of links. We can determine whether passengers’ temporal and spatial positioning coordinates well with others. In the simple matching network, we find 13 isolated nodes. Those correspond to travellers who rejected all possible shared rides, regardless of the sampled $\varepsilon$. In contrast, we find a single traveller who always shared a ride. He participates in 90 different shared rides during the simulation. Other passengers either formed shared rides frequently or only under favourable conditions. The most stable pooled ride occurred in 567 replications. We find that 48% of travellers effectively shared a ride in at least half of the replications. These results highlight the sensitivity of the pooling system to the individual preferences.

Fig. 6

Weighted network structures. Simple form in the first row, exact in the second. Shareability networks in the first column, matching networks in the second. Link thickness denotes the link probability (share of occurrences across the replications)

3.6 Evolution of probabilistic ride-pooling networks

Here, we report how the graph structures evolve across the replications. We analyse how the average degree and size of the greatest component change when the ride-pooling problem is replicated. The weighted structures accumulate all previous replications. Therefore, they are (weakly) growing networks. (New links and nodes may appear in consecutive replications.) Here, we report on this growth.

The evolution of the two measures with replications is shown in Fig. 7. The stabilising trend of the greatest component (blue) suggests that 1000 replications are sufficient, yet the average degree (green) increases even in the latter replications.

Fig. 7

Evolution of the topological properties of the simple matching graph in respective replications

To determine stability of the higher-order rides, we consider the exact, bipartite network representation. Figure 8 demonstrates the evolution of the bipartite matching networks, snapshot after 1, 5, 10, 100 and 900 replications. Number of rides increased twofold (from 732 to 1512) between 100-th and 900-th step indicating a high sensitivity of the pooling system. This, combined with results from the previous figure, suggests that final matches are not stable and new rides appear even after sufficiently high number of replications.

Fig. 8

Evolution of the bipartite matching between travellers (left) and rides (right)—snapshots after respective number of replications

4 Conclusions and discussion

In our study, we formalise and explicitly analyse network structures of ride-pooling. First, the network is constructed at the stage of finding feasible rides; second, at the stage of identifying the optimal solution. At both stages, we distinguish between simple and exact representations. We first consider deterministic networks (where link generation function is deterministic), which we further extend to the probabilistic cases where networks become probabilistic and the number of occurrences in replications is interpreted as the link probability. All four network structures have significantly different properties and interpretations, jointly creating a complex insights into ride-pooling problems. The already different properties of the networks have different variabilities when the networks become probabilistic.

We run two simulations with the implicit link generation formula, to better understand the network properties. First, we keep the demand fixed and incrementally increase the sharing discount (which makes the network evolve from sparse, disconnected towards fully wired) and observe transition in the topology. We find a high correlation between the topological properties and the ride-pooling system performance. Correlations above 0.9 are observed, indicating a close to linear relation. Our results suggest that the shareability networks itself can be a powerful proxy for estimating pooling performance, which has a great potential, e.g. for large-scale problems for which solving the ride-pooling problem becomes computationally expensive or impossible.

We investigated properties of probabilistic networks when uncertainty at the traveller level was introduced into our model. Random variable represents different attitudes towards pooling across travellers. We find that a relatively small random terms in link generation formulas have a significant impact on networks and pooling performance. Next, we introduce weighted networks obtained via different realisations of the variables, where links are no longer binary (present or absent), but also have a weight (corresponding to the probability of their occurrence). We study not only the shareability structures, which represent an algorithmic step but also the matching structures representing the actual realisation of the pooling. We analyse the evolution of the weighted networks and the stability of certain links, observing on one hand huge numbers of low-probability links (number of rides increased twofold between 100-th and 900-th replication), and on the other the stable links with high probability (the most frequently occurring shared ride appeared in 56% of the replications).

Strong correlation between graph properties and ride-pooling performance indicators is an important highlight with the variety of applications, including, e.g. machine learning techniques. For the purpose of training, one should define an easily computable function. While the exact solution is time-requiring, simple approximations based on graph topology could be a valuable proxy to this complex problem.

Formalising a class of networks allows for a broad spectrum of graph theory methods to be applied in the context. Different representations of the underlying network structures facilitate spreading analyses. One can use it, e.g. in the graph decomposition problems, involving deep graph neural networks, such that the pooling performance (measurable on the matching network) is not hindered and simultaneously communities become isolated reducing virus spreading (measurable on the shareability network).

The stochastic approach in the utility formulation, resulting in the proposed weighted networks, leads to novel assessment methods. Edges can be now assigned a probability of their occurrence in the system, which allows to apply rich methodology on weighted probabilistic networks, e.g. to better estimate the expected ride-pooling performance.

In the future, this analysis shall be extended to better reflect the heterogeneity of ride-pooling behaviour reported in recent studies. Also, this analysis was performed on a single demand pattern, which is not necessarily generalisable for other demand levels and spatio-temporal distributions of trip requests.