1 Introduction

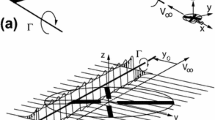
In 1937, Henrich Focke gave a lecture about the development of his helicopter FW-61 in the AVA (Aerodynamic Research Institute in Göttingen, Germany, nowadays DLR) see [1]. In this lecture, he discussed in detail the various measures to compensate the reaction torque of helicopter rotors. The original sketch from Focke’s talk is presented in Fig. 1: Two counter-rotating rotors on top of each other’s, realized by Breguet, d’Askanio, Pescara, Asboth (a), two rotors behind each other, Cornu or four rotors at the edge of a square, de Bothezat, Oehmichen (b); two counter-rotating rotors side by side, Focke, Berliner and Kaman, Flettner with intermeshing rotors (c); two equal rotating rotors with the shaft set such, that the total moment is compensated, Florine, Belgian Government (d); a large rotor with small propellers on the blades, Isacco, Curtis-Bleeker (e); actuation of the rotor blades by flapping motion, Küssner (f); a single rotor with a tail rotor, Sikorsky, Baumhauer, Holl (g); backwards blowing propellers with guiding vanes in their slip stream, Hirtenberger Austria (h); guiding vanes directly inside the rotor slip stream, Hafner, Nagler (i); jet propulsion used to rotate the single rotor, Dornier, Papin, Roully, France (k).

Fig. 1
figure 1

Methods to compensate the reaction moment, after H. Focke, [1]

Full size image

In the present paper, special emphasis will be placed on case (f): a helicopter body with only one single rotor.

In [2] Küssner has described the details of his concept. Creating a flapping motion of the rotor blades, he constructed a device which mechanically forced the rotor blades to run in a plane tilted rigidly to the rotor axis by an angle say ϑ. It has to be kept in mind that the aircraft has to be trimmed particularly in roll.

This means for each blade section to experience a 1/rev flapping motion with a flapping amplitude depending on the radius of the section: r ϑ, the flapping period coincides with one cycle of the rotor rotation, thus rotor rotation frequency and flapping frequency coincide.

Küssner constructed a wind tunnel model with variable tilt angle ϑ of the rotor and was able to show that the torque as a function of ϑ could be reduced to zero, thus fulfilling his objectives. However, it should be mentioned at this point that the rotor working under zero torque condition could not automatically fulfill the problem of creating the necessary rotor thrust to keep the model aloft.

Using numerical calculations, at various blade sections, [3] and combining the results with the simple blade element theory, [4] a remarkable agreement with Küssner´s experimental data was found.

But it was obvious that a pure flapping motion was not sufficient to meet both goals:

  1. (1)

    Torque compensation

  2. (2)

    Sufficient rotor thrust

Careful study of animal flight has shown, that pure flapping motion is not sufficient to fly efficiently. Investigations of a flapping model rotor (the Ornicopter Project, [5]) have shown that the reaction moment of the rotor could be compensated; however, it was not possible creating the necessary rotor thrust at the same time to lift the model from the ground. Major drawbacks of the original design have been corrected, see [6, 7].

A 1/rev Pitching motion has to be added including a special phase difference between pitch and plunge. First results are documented in [8].

In the present paper, the physical aspects of the flapping rotor problem will be highlighted more in detail: A first and important step to understand the problems will be the investigation of a blade set with pure plunging motion. It will be shown that flow separation is the limiting factor here. Following this, the combination of pitch and plunge is investigated. It is shown that the ratio of both induced incidence amplitude of the plunge motion and the amplitude of the pitch motion as well as a necessary phase shift between both motions is of crucial importance for a successful construction.

2 Flapping (plunging) motion

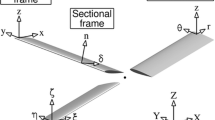
Figure 2 show the blade arrangement and notations. The rotor plane is tilted against the rotor axis by the tilt angle ϑ. The vertical displacement of a blade section at radius r becomes:

$$z = r\;R\;{\text{sin}}(\vartheta )\;{\text{cos}}(\omega t)$$
(1)

with the flapping frequency ω = Ω (Ω = Rotation-frequency). Differentiation of (1) with respect to time gives the velocity of flapping motion:

$$\partial z/\partial t = - \omega \;r\;R\;{\text{sin}}(\vartheta )\;{\text{sin}}(\psi)$$
(2)
Fig. 2
figure 2

a Sketch of blade motion (υ ≡ ω, ψ = ωt) z normal to horizontal plane. b: Angle of attack during start of up-stroke red airfoil at α = 0o

Full size image

In a blade fixed frame of reference, the sign in (2) has to be changed (Fig. 2b), to be consistent with the definition of boundary conditions in the calculations. In a space fixed frame, the kinematic velocity ∂z/∂t is positive upwards. A viewer in the blade fixed system however “sees” a negative, i.e., downward velocity. The same holds for the horizontal velocity: u is defined positive in the blade fixed system, although the rotation speed points in the negative direction, Fig. 2b.

In dimensionless terms, with:

$$\omega^*\left(r\right) = \omega \;c/\left( {r\;R\;\Omega } \right) = c/\left( {r \, R} \right);T\left( r \right) = tr\;R\;\Omega /c$$
(3)

as the section reduced frequency (the most important unsteady flow parameter and input for the Navier–Stokes calculations).

With ∂z/∂t, the vertical flapping speed and u = r R Ω, the horizontal section speed:tan θh = ∂z/∂t/u and with (2)

$$\theta_{{\text{h}}} = {\text{arctan}}\left[ {{\text{sin}}\left( \vartheta \right)\;{\text{sin}}\left( \psi \right)} \right],\;\psi = {2}\pi {\text{Time}}{.}$$
(4)

The flapping angle θh represents a sin-wave with a positive maximum at 25% of the rotation period and a minimum at 75% respectively.

3 Pitching motion

The pitching motion of each blade is represented by two different terms:

$$\theta_{{\text{p}}} = \alpha + \theta_{{\text{c}}} \,{\text{cos}}\,(\omega^*T + \phi)$$
(5)

With a steady part α, and a time-dependent part (amplitude θc). Φ is the phase shift between pitch and plunge motions.

Taking into account a linear twist of the blade, its steady angle is further defined as:

$$\alpha = \theta_{0} + \theta_{{{\text{tw}}}} r$$
(6)

With θ0 as the steady blade pitch angle (at r = 0) and θtw as the linear (negative) twist rate, [4]. The phase shift Φ is assumed to be 90° which has been shown to be close to an optimum, [8].

4 Combination of plunge and pitch motions

Adding Eqs. (4) and (5) and considering a uniform inflow, yields

$$\theta = \theta_{{\text{h}}} + \theta_{{\text{p}}} - \lambda /r$$
(7)

where λ represents the inflow ratio. The negative sign of λ in Eq. 7 is caused by the flow through the rotor disk downwards, i.e., the corresponding angle is negative. λ/r adds to the steady part α of Eqs. 5 and 6. Within the scope of blade element theory and the assumption of hover flight condition, the inflow ratio is defined as

$$\lambda =\frac{\sigma \times a}{16}\times \left[\sqrt{\left(1+\frac{64\times {\theta }_{.75}}{3\times \sigma \times a}\right)}-1\right]$$
(8)

with [4]:a = airfoil lift slope σ =  rotor solidity θ.75 =  collective pitch angle at 75% rotor radius R.

The term λ/r can be assumed as a steady correction angle due to the induced flow downward through the rotor disk representing a negative incidence correction. θp in Fig. 2b includes the steady term λ/r

5 Blade element theory, [4]

Notations are taken from [4]. Exception is the blade thrust due to blade flapping which has to be combined with the drag force to get Ct(r).

The mean section force parallel to the reference plane is defined as:

$${C}_{t}(r)={\int }_{0}^{1}{c}_{t}\left(r,\mathrm{Time}\right)\, d\, \mathrm{Time}$$
(9)

Mean section power coefficient:

$${C}_{p}(\mathrm{r})={\int }_{0}^{1}{c}_{P}(r,\mathrm{Time})\,d\,{ \mathrm{Time}}$$
(10)

etc.with Time as the normalized time (referred to one period of rotation).

The time-averages are then integrated along the blade radius:

5.1 Rotor thrust

$${C}_{T} = \sigma /2\int_{0}^{B} {C_{l} (r)r^{2} dr} ;$$
(11)

With Cl (r) = section lift force. The effective outer boundary B = 0.95, takes care of tip losses, [4].

5.2 Torque

$${C}_{Q} = \lambda {C}_{T} - \sigma /2\int_{0}^{1} {C_{t} (r)r^{3} dr}$$
(12)

CQ in Eq. (12) can be expressed by the two terms: CQ = CQi – CQ0 with CQi = λCT as induced power loss, [4]. Different to [4], CQ0 now represents the sum of drag and blade thrust of the flapping blade and determines the sign of CQ0 (negative if drag is dominant and positive if blade thrust dominates). The upper boundary of integration for the skin friction drag (as part of Ct) has to be extended to 1.

6 Results

6.1 Pure flapping

First studies are focused on the rotor with pure flapping blades to show the limitations of this arrangement. In this case, the reaction moment can be compensated due to the development of sufficient blade thrust.

However, the necessary rotor thrust may not be large enough to lift the body weight from the ground. The investigations are concentrated on hover conditions as the most critical flight condition.

The calculations are carried out in 3 different steps:

  1. (1)

    Navier–Stokes calculations, [9] at four selected radial blade sections:

Section 1: r = 0.29

Section 2: r = 0.48

Section 3: r = 0.60

Section 4: r = 0.86

  1. (2)

    Spline interpolation of the section coefficients between r = 0.2 and r = B.

  2. (3)

    Integration of blade coefficients for a complete four-bladed rotor.

The OA209 airfoil section has been selected for the present calculations. This airfoil has been used for several helicopter projects. The coordinates are freely available in literature. For simplicity, the Mach and Reynolds numbers are assumed to be constant with Ma = 0.1 and Re = 105. The numerical calculations are done fully turbulent taking into account the Spalart/Allmaras turbulence model, [10].

Figure 3 shows the angles of attack and lift of the airfoil Section 4 (r = 0.86) with pure flapping motion. The blades are twisted with θ0 = 16° and θtw = – 8°. Using Eq. (8) with σ = 0.1273 and a = 5.556 (lift slope of OA209 at zero lift) the inflow ratio λ = 0.0664 and the effective steady angle αe = α – λ/r = 4.7° (steady part of Eq. (7) with θp = αe and θc = 0, Eqs. (5) and (6).

Fig. 3
figure 3

Incidence variation, pure plunge, ϑ = 8o

Full size image

The green curve in Fig. 3 represents the flapping angle θh, the blue curve is the sum of θ = θh + αe. The magenta curve represents the lift curve (multiplied by a factor of ten for better visibility). The lift curve shows already the start of separation at about Time = 0.5.

In Fig. 4 (ϑ = 12°), the angle θ exceeds 15° at Time = 0.25 and the lift curve shows a severe breakdown due to flow separation. The section lift reduces from Cl = 0.42 to Cl = 0.34.

Fig. 4
figure 4

Incidence variation, pure plunge, ϑ = 12o

Full size image

Figures 5 and 6 present the various coefficients: ct(r, T) = – cx(r, T) (blue, green), cP(r, T) (magenta), etc. in correspondence to Fig. 3. The terms: cxf and cxp represent skin friction drag and pressure drag respectively. η means section efficiency: η = Ct/Cp. Integrating these terms with respect to time, the section coefficients Ct and Cp are obtained. There is no sign of flow separation, different to Fig. 3 (showing a small deviation of cl from a sin-wave).

Fig. 5
figure 5

Section coefficients, pure plunge, ϑ = 8o

Full size image
Fig. 6
figure 6

Section coefficients, pure plunge, ϑ = 12o

Full size image

At tilt angle ϑ = 12°, Fig. 6, the first half of the period shows severe separation effects corresponding to Fig. 4. The efficiency ɳ (ratio of Ct/Cp) is reduced from 0.53 (Fig. 5) to only 0.43. Further, Eqs. (11) and (12) are applied, i.e., integrate the section forces and moments along the radius of the 4 rotor blades. As an example, Fig. 7 shows the integrands of Eq. (12) versus radius for a set of tilt angles ϑ. The 4 radial section coefficients have first been interpolated by a spline interpolation procedure (Akima splines, dashed lines) and then integrated between r = 0.2 and r = 1. The results are CQ0 values are listed in Fig. 7. Up to ϑ = 10°, the curves are smoothly increasing, at ϑ = 12° the corresponding curve shows reductions in the tip region which are again a consequence of flow separation (see Figs.4 and 6). Finally, the induced power loss CQi = λCT is calculated. Then applying Eq. (12), the combined results are plotted in Fig. 8. The red curve in Fig. 8 represents the rotor torque CQ which cuts the zero line at ϑ = 8.4°. At this tilt angle, the rotor rotates without reaction torque. It remains to be shown how large the lift coefficient is at this tilt angle. This will be investigated in the following sections.

Fig. 7
figure 7

Example of radial integration for CQ0

Full size image
Fig. 8
figure 8

Power and torque for 4-bladed rotor, pure plunge

Full size image

Figure 9 presents the surface pressure distributions (for these figures also named: cp) as results from the Navier–Stokes calculations (along the blade upper surface at time instants Time = 0.30 and 0.32). In both cases, separation is severe at tilt angle ϑ = 14°, (right margin of Fig. 8). This can also be detected in Figs. 9: A pressure low (pressure signs in Figs. 9 are multiplied by – 1) is formed at the leading edge of the blade close to the blade tip. This pressure low moves over the upper surface and disappears into the wake. At the remainder of the upper blade surfaces, the flow is smooth. On the lower surface (not shown), no separation is present.

Fig. 9
figure 9

Surface pressure distributions, a Time = 0.30, upper blade surface, ϑ = 14°. b Time = 0.32, upper blade surface, ϑ = 14°

Full size image

6.2 Combined flapping and pitching motions

In the previous section, a single rotor with pure flapping motion was investigated. It was demonstrated that the reaction torque could be compensated at a rotor tilt angle of ϑ = 8.6°. In the tip region of the rotor blade, the maximum angle of attack is already close to flow separation. In this case, the corresponding rotor thrust is not sufficient to lift the attached body weight from the ground.

7 To reach the objectives, a 1/rev pitching motion with phase offset is added

Two parameters have to be specified in particular:

  1. (a)

    A phase shift between plunge and pitch: Φ in Eq. (5).

  2. (b)

    A proper ratio between the induced flapping and pitching amplitudes ϑ/θc.

The vertical displacement of the airfoil section due to flapping yields z ~ cos(ψ) (Eq. 1). The angle variation of the pitching motion corresponds to θp ~ cos (ψ + Φ), Eq. (5). It has been outlined in [8] that a phase shift of Φ = 90° leads to optimum results. Therefore, Φ = 90° has been chosen in the present paper as a fixed parameter although this is not necessary. With a phase shift of 90°, it is obvious that plunge motion and pitch motion are 90° out of phase where pitch leads plunge.

Figure 10 shows the time variations of the different angles and the lift (multiplied by a factor of 10). In particular, the red curve (cyclic pitch) is now varying with time, different to Figs.3 and 4 where this term was zero. At Time equal zero in Fig. 10, the red (and blue) curves have an offset of αe = 4.73° due to the steady part of the pitch angle.

Fig. 10
figure 10

Incidence variation, pitch/plunge, ϑ = 20°

Full size image

As before a linear blade twist has been applied again: α = θ0 + θtwr, Eq. (6). With θ0 = 16° and θtw = – 8°, θ.75 = 10°.θ.75 is used in Eq. (8) to determine the constant inflow rate λ of the rotor, here λ = 0.0664.

The most important effect of the phase shift in Eq. (5) leads to a sectional time variation for θp ̴ cos (ω*T + Φ) = – sin (ω*T). The corresponding time variation of the flapping motion yields θh ̴ + sin (ω*T) (Eq. 4). Both pitching and flapping angles are 180° out of phase which is shown in Fig. 10 as red and green curves. The result is the difference of both curves (blue curve) including the steady parts: αe = α – λ/r (α from Eq. (6), λ/r from Eqs. (7), (8)). The magenta curve represents the lift variation (multiplied by 10). The lift shows first signs of separation at a maximum flapping angle of almost ϑ = 20°.

The pitching amplitude reduces the effective incidence to about 14°.

The section lift: Cl = 0.42 in Fig. 10 is in the same order of magnitude as for the pure plunging case of Figs. 3 and 4. But now θc (pitch amplitude) can be varied within a wider margin to adjust the section lift and therefore the rotor thrust to higher values.

Figure 11 displays the various section coefficients versus one time period. Of special concern is the ratio Ct/CP: section thrust versus section power which is indicated in Fig. 11 as ɳ = 0.808. This is a very high value at the high flapping incidence of ϑ = 20 o and obviously at the start of flow separation which can be seen in Fig. 10 for the section lift. The lift curve shows clearly deviations from a sin-curve between Time = 0.4 and 0.6.

Fig. 11
figure 11

Section coefficients, pitch/plunge, ϑ = 20°

Full size image

For the next step, the section coefficients are again integrated along the blade radius, taking into account Eqs. (11) and (12) respectively. The results are included in Fig. 12 showing two distinct regions which will be specified next:

Fig. 12
figure 12

Power and torque for 4-bladed rotor, pitch/plunge, θc = 10°, θ.75 = 10o

Full size image

It has already been mentioned in the introduction, that the ratio of flapping and pitching incidence–amplitudes ϑ/θc are of special concern. In the present case, θc = 10°. Therefore, at ϑ = 10°, the energy transfer changes its direction. For ϑ < 10°, energy is transferred from the fluid into the oscillating system as has already been outlined in [11]. Although this area is not of concern for the present study, it is necessary to understand the correlations. Two problems may be important in this regime:

  1. (1)

    The flutter problem i.e., torsion bending of an airplane wing or control surface where energy from the fluid increases the flapping amplitude to dangerous conditions.

  2. (2)

    The problem to harvest energy from the fluid under optimized conditions, [12].

For ϑ > θc, the energy transfer changes direction, energy is now transferred from the flapping system into the fluid. This transfer is coincident with the development of blade thrust. Increasing blade thrust creates torque CQ in direction of rotation. The torque due to blade thrust counteracts the reaction torque until zero (total) torque is realized (the red curve in Fig. 12 cuts the zero line). The zero point is reached at ϑ = 15.0o

The black dashed curve in Fig. 12 represents the power consumption due to the flapping blade motion. The black solid curve is the total power consumption adding the power at ϑ = 0°: CP0. Finally, the green curve is the sum of CQ + CP and represents the power to be provided by a motor driving the rotor (aerodynamic part). This curve is surprisingly slightly lower than CP0 and increases beyond ϑ = 20° when the flow at the blade tips starts to separate.

The following steps are necessary to increase the level of rotor thrust: Increase the steady blade pitch angle of the twisted blade at 75% radius to θ.75 = 12° and adjust the pitch amplitude to θc = 12°.

The results are displayed in Fig. 13. In this case, data are only plotted for the region ϑ > θc. In the present investigation, this restriction is sufficient: The cut of the zero line for total torque CQ (CQ = 0 at ϑ = 17.6°) is of major concern.

Fig. 13
figure 13

Power and torque for 4-bladed rotor, pitch/plunge, θc = 12°, θ.75 = 12o

Full size image

A further case with θc = 12° and θ.75 = 14° is displayed in Fig. 14. In this case, CQ is cutting the zero line at ϑ = 18.8°. In all cases, the compensation of the reaction torque is definitely within the non-separated flow regime of the rotor blades.

Fig. 14
figure 14

Power and torque for 4-bladed rotor, pitch/plunge, θc = 12°, θ.75 = 14o

Full size image

To confirm that separation does not take place even at tilt angles higher than 20°, Fig. 15a and b again shows the pressure distributions on the upper surface of the blade. Now flapping and pitching motions are combined.

Fig. 15
figure 15

Surface pressure distributions, a Time = 0.30, upper blade surface, ϑ = 22°, θ c = 12°, θ.75 = 12°. b Time = 0.32, upper blade surface, ϑ = 22°, θ c = 12°, θ.75 = 12°

Full size image

The parameter combination of Fig. 13:θc = 12°, θ.75 = 12°has been selected. At both time instants (Time = 0.30 and 0.32), the surface pressures along the blade radius are very continuous which is quite different to the pure flapping cases displayed in Fig. 9a and b where severe separation is present. Now only the trailing edge area at the blade root (lower surface) shows the beginning of a small separation area which does not have a larger influence on the blade forces and moments (not shown).

Finally, in Fig. 16, the blade loads CT/σ versus the tilt angle ϑ are plotted for all cases investigated.

Fig. 16
figure 16

Blade loadings, all cases investigated

Full size image

In all curves, the points of zero CQ (torque compensated) are indicated (square symbols). The magenta curves belong to the pure flapping case and show a different behavior compared to the pitch/plunge combinations. For the latter cases, the zero CQ-points are aligned along the black dashed curve in Fig. 16.

It is obvious that the increase in the pitch amplitudes θc from 10° to 12° combined with the increase of the steady blade pitch angles θ.75 step by step, is lifting the level of rotor thrust up to a blade loading of CT/σ > 0.09. In all cases, severe flow separation is completely avoided.

In Fig. 16, the most important result of all calculations can be studied: zero torque (square symbols) can be adjusted to higher rotor thrust levels.

This meets the objectives to develop a single rotor which:

  1. (a)

    Compensates its reaction torque and

  2. (b)

    At the same time develops enough rotor thrust to lift the attached body from the ground.

The two magenta curves in Fig. 16 represent pure plunging motion at zero blade twist (dashed curve) and with linear twist (solid curve). In both cases, the blade loadings remain very low although the reaction torques could also be compensated in these cases.

8 Lessons learned from the present investigations

It has been pointed out in the preceding sections that a flapping motion with one per rev flapping frequency is sufficient to compensate the reaction torque of a single rotor. However, the blade lift, forming the rotor thrust, will hardly be sufficient to lift a body from the ground.

To change this deficiency, a 1/rev pitching motion of the blades, has to be added. If flapping and pitching motions are 90° out of phase, the flapping and pitching angles are in anti-phase.

The situations can best be seen in the section angle of attack variations of the different parts. If only flapping is involved, the flapping angle during a time period is added to the effective steady angle of attack αe = α – λ/r with α as the steady blade pitch angle of the twisted blade and λ/r as the inflow correction. In Fig. 3, the flapping amplitude is only ϑ = 8°, the steady effective angle of attack is αe = 4.70°. The sum θ is almost 13° at Time = 0.25 which is at the edge of flow separation. The section lift remains on a low level, Cl ≈ 0.42 with a corresponding low level of blade loading (see Fig. 16).

The situation changes completely if cyclic pitch is added (see Fig. 10). Flapping and pitching angles are in anti-phase (red and green curves in Fig. 10). The pitching motion is acting about αe as the steady mean pitch angle. The sum of all angles is represented by the blue curve θ with the maximum at about 14°. This is at the edge of separation as the lift (magenta) curve in Fig. 10 is indicating. Torque compensation is reached at ϑ = 15.0° (see Fig. 12).

Now the steady blade pitch angle (collective pitch) α can be increased step by step as has been done in further steps. To avoid flow separation on the blades, the pitch amplitude has always to be adjusted in such a way, that the maximum angle θ of the flapping and pitching blade does not exceed about 13° to avoid flow separation. It is shown in Fig. 16 that the thrust level is increased considerably and the points of zero reaction torque are still within the secure non-separated range.

It must be kept in mind that for an airfoil with positive camber (OA209), limited negative angles of attack have to be considered to avoid that separation occurs on the lower blade surface during the second half of the oscillation period. In the present parameter variations, this limit could be realized.

Additional effort has to be taken in order to construct a real flying vehicle including flapping blade motion to develop blade thrust and a rotor torque which is sufficient to compensate the reaction torque. The present paper shows the aerodynamic principals for a successful design and shows that a design with a single rotor is possible. All other necessary questions have to be answered in addition.

In particular, a disk-tilting moment may remain which could probably be avoided by higher-harmonic prescribed motion, for example at 2/rev. A saddle-like motion of the blade tips may be seen in Fig. 1f as introduced by H. Focke (dashed line in Fig. 1f).

9 Conclusions

In the early days of helicopter development, a reasonable number of cases have been proposed to compensate the reaction torque of the rotor. The possibility to use a rotor with flapping blades has not been given much attention nowadays, but it is worth looking into the details of its working mechanism. Why and how insects and birds and other animals are able to fly was known long before helicopters could fly. It was clear that a pure up-and-down (flapping) motion of the wings is not very efficient to produce the necessary thrust for forward flight and at the same time develop enough lift to keep the body aloft.

Pitching motion with a phase shift has to be added to increase the flight envelope of the animal considerably.

With this optimized solution of nature in mind, the present investigation for rotors has been investigated: The flapping mode is realized by tilting the tip path plane of the rotor blades (flapping or plunging mode) and adding cyclic pitch with a special phase shift between modes. With this combination of plunge and pitch, it could be shown that

  1. (1)

    The point of zero torque

  2. (2)

    The necessary rotor thrust

both could be realized by changing the necessary parameters available to match the objectives. In [2], it has already been shown that pitch has to be added for a sufficient design and it was already clear at this time that animal flyers provide an excellent model.

The present results are obtained numerically. It has already been shown before, [3] that in comparison with experimental data, [2] good comparisons have been found.