Skip to main content
SpringerLink
Log in

Wind-tunnel studies on maneuvering slender bodies

  • Original Paper
  • Published:
CEAS Aeronautical Journal Aims and scope Submit manuscript

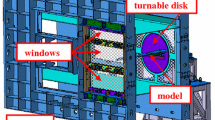
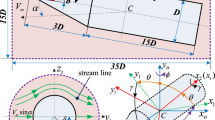
Abstract

In this paper, the first experimental results of tests with a new model support designed for simulations of high frequency and high amplitude pitching maneuvers are presented. A generic missile model with a blunt nose was used for which static test data from earlier experiments with a conventional model support were existing. At the beginning, static tests were done for comparison purposes to judge the influence of the new setup (model support, sting for the model, pivot arm) on the measured forces and moments. Afterwards, dynamic tests with sine oscillations at frequencies of \(f_{\rm a}=0.05\ldots 4\,\hbox{Hz}\) and angles of attack varying between \(\alpha = 0^{\circ} \ldots 45^{\circ}\) were performed. Beside the qualification of this new test rig, the tests were used to study the “Phantom Yaw Effect” and to prove an interactive method of its control. This phenomenon is characterized by unwanted yawing moments resulting from asymmetric vortices which can occur on slender bodies at high angles of attack. In the tests, a lee-vortex control device with symmetrically arranged longitudinal slot nozzles producing “air-jet strakes” was demonstrated to decrease the yawing moments both under static and dynamic conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Notes

  1. With "nominal amplitudes of the AoA", the nominal or target values of the rigging angle of incidence is meant. This AoA differs from the real AoA because it neglects the deflection of the sting resulting from the aerodynamic and inertial loads acting on the model.

  2. SIKA-R 30 IS: viscosity coefficient \(\alpha_{\rm perm} = 17\times 10^{-12}\,\hbox{m}^2,\) inertia coefficient \(\beta_{\rm perm} = 25\times 10^{-7}\,\hbox{m}\) (according to German DIN ISO 4022); both coefficients describe the permeability of this material.

  3. By the help of the parallel axis theorem, the mass moment of inertia of a rigid body can be determined for an axis (2) parallel to an axis (1) through the CG of the body. The mass moment of inertia has to be known for axis (1). The additional term is \(m\cdot r^2\) with m the mass of the body and r being the perpendicular distance between both axes. The resulting formula is: \(J_2 = J_1 + mr^2\) with J the mass moment of inertia.

Abbreviations

α :

Angle of attack

\(\Updelta\alpha\) :

Pitching amplitude

\(\alpha_{\rm AV}\) :

Onset angle asymmetric vortices

\(\alpha_{\rm SV}\) :

Onset angle symmetric vortices

\(\alpha_{\rm UV}\) :

Onset angle unsteady vortices

\(\alpha_{\rm N}\) :

Effective angle of attack at model’s nose

δ :

Offset angle of x-axis and radius to pivot for a POI

ω :

Angular velocity

\(\dot{\omega}\) :

Angular acceleration

σ :

Standard deviation

a :

Acceleration

\(c_x, c_y, c_z\) :

Aerodynamic force coefficients

\(c_l, c_m, c_n\) :

Aerodynamic moment coefficients

\(c_{x,{\rm {bp}}}\) :

Axial force coefficient at model base

D :

Model diameter

\(F_x, F_y, F_z\) :

Force in X-, Y- or Z-direction

\(F_{\rm act}\) :

Actuation force of hydraulic system

\(f_{\rm a}\) :

Actuation frequency

\(f_{\rm s}\) :

Sampling frequency

J :

Moment of inertia

L :

Model length

M :

Mach number

\(M_x, M_y, M_z\) :

Moment around X-, Y- or Z-axis

m :

Model mass

\(q_\infty\) :

Free stream dynamic pressure

\(p_\infty\) :

Free stream static pressure

\(p_0\) :

Stagnation pressure

\( p_{\rm B}\) :

Base pressure

\(Re_D\) :

Reynolds number (based on model diameter)

r :

Distance to the pivotal point

t :

Time

\(t_{\rm m}\) :

Measurement time

\(\Updelta x\) :

Distance between 2 points on x-axis

\(\Updelta z_0\) :

Distance wind tunnel wall to main body axis

AoA:

Angle(s) of attack

BRP:

Balance reference point

CAD:

Computer-aided design

CG:

Center of gravity

DLR:

German Aerospace Center

MCS:

Model coordinate system

MEMS:

Microelectromechanical systems

POI:

Point of interest

RCS:

Rotation coordinate system

RMS:

Root mean square

RP:

Reference point

RS:

Reference (coordinate) system

TWG:

Transonic wind tunnel Göttingen

x :

X-direction of corresponding coordinate system

y :

Y-direction of corresponding coordinate system

z :

Z-direction of corresponding coordinate system

M:

Model (coordinate system)

N:

Model nose

CG:

Center of gravity

Acc:

Accelerometer parameter

in:

Inertial

BRP:

Referring to balance reference point

bpc:

Base pressure corrected

References

  1. Ericsson, L.E., Reding, J.P.:Steady and unsteady vortex-induced asymmetric loads on slender vehicles. J. Spacecr. 18(2), 97–109 (1981)

    Article  Google Scholar 

  2. Ericsson, L.E., Reding, J.P.: Asymmetric flow separation and vortex shedding on bodies of revolution. Prog. Astronaut. Aeronaut. 141, 391–452 (1991)

    Google Scholar 

  3. Hunt, B.L.: Asymmetric vortex forces and wakes on slender bodies. AIAA Paper, 82–1336 (1982)

  4. Montividas, R., Reisenthel, P., Nagib, H.: The scaling and control of vortex geometry behind pitching cylinders. AIAA, 89–1003 (1989)

  5. Ng, T.T., Malcolm, G.N.: Forebody vortex control using small, rotatable strakes. J. Aircr. 29(4), 671–678 (1992)

    Article  Google Scholar 

  6. Patel, M.P., Tilmann, C.P., Ng T.T.: Closed-loop missile yaw control via manipulation of forebody flow asymmetries. J. Spacecr. Rocket. 41(3), 436–443 (2004)

    Article  Google Scholar 

  7. Smith, L.H., Nunn, R.H.: Aerodynamic characteristics of an axisymmetric body undergoing a uniform pitching motion. J. Spacecr. 13(1), 8–14 (1976)

    Article  Google Scholar 

  8. Zeiger, M.D., Telionis, D.P.: Vortex asymmetry over Ogive cylinders in coning and pitching motions. AIAA 96-0206 (1996)

  9. Zeiger, M.D., Telionis, D.P., Vlachos, P.P.: Unsteady separated flows over three-dimensional slender bodies. Prog. Aerosp. Sci. 40, 291–330 (2004)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. German Aerospace Center (DLR), Institute of Aerodynamics and Flow Technology (AS), Bunsenstraße 10, 37073, Göttingen, Germany

    O. Wysocki, E. Schülein & H. Rosemann

Authors
  1. O. Wysocki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Schülein
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H. Rosemann
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. Wysocki.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wysocki, O., Schülein, E. & Rosemann, H. Wind-tunnel studies on maneuvering slender bodies. CEAS Aeronaut J 4, 123–138 (2013). https://doi.org/10.1007/s13272-012-0051-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13272-012-0051-y

Keywords

Search

Navigation