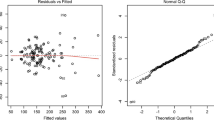
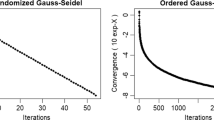
Statistical analyses of two-way tables with interaction arise in many different fields of research. This study proposes the von Mises–Fisher distribution as a prior on the set of orthogonal matrices in a linear–bilinear model for studying and interpreting interaction in a two-way table. Simulated and empirical plant breeding data were used for illustration; the empirical data consist of a multi-environment trial established in two consecutive years. For the simulated data, vague but proper prior distributions were used, and for the real plant breeding data, observations from the first year were used to elicit a prior for parameters of the model for data of the second year trial. Bivariate Highest Posterior Density (HPD) regions for the posterior scores are shown in the biplots, and the significance of the bilinear terms was tested using the Bayes factor. Results of the plant breeding trials show the usefulness of this general Bayesian approach for breeding trials and for detecting groups of genotypes and environments that cause significant genotype × environment interaction. The present Bayes inference methodology is general and may be extended to other linear–bilinear models by fixing certain parameters equal to zero and relaxing some model constraints.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Burgueño, J., Crossa, J., Cornelius, P. L., and Yang, R.-C. (2008), “Using Factor Analytic Models for Joining Environments and Genotypes Without Crossover Genotype × Environment Interaction,” Crop Science, doi:10.2135/cropsci2007.11.0632.
Chib, S. (1995), “Marginal Likelihood From the Gibbs Output,” Journal of the American Statistical Association, 90, 1313–1321.
Cornelius, P. L., and Seyedsadr, M. S. (1997), “Estimation of General Linear–Bilinear Models for Two-Way Tables,” Journal of Statistical Computation and Simulation, 58, 287–322.
Cornelius, P. L., Seyedsadr, M. S., and Crossa, J. (1992), “Using the Shifted Multiplicative Model to Search for ‘Separability’ in Crop Cultivar Trials,” Theoretical and Applied Genetics, 84, 161–172.
Cornelius, P. L., Crossa, J., and Seyedsadr, M. S. (1994), “Tests and Estimators of Multiplicative Models for Variety Trials,” in Proceedings of the 1993 Kansas State University Conference on Applied Statistics in Agriculture, Manhattan, Kansas.
Cornelius, P. L., Crossa, J., and Seyedsadr, M. S. (1996), “Statistical Tests and Estimators of Multiplicative Models for Genotype-by-Environment Interaction,” in Genotype-by-Environment Interaction, eds. M. S. Kang and H. G. Gauch, Boca Raton: CRC Press, pp. 199–234.
Crossa, J., Yang, R.-C., and Cornelius, P. L. (2004), “Studying Crossover Genotype × Environment Interaction Using Linear–Bilinear Models and Mixed Models,” Journal of Agricultural, Biological, and Environmental Statistics, 9, 362–380.
Crossa, J., Perez-Elizalde, S., Jarquin, D., Cotes, J. M., Viele, K., Liu, G., and Cornelius, P. L. (2011), “Bayesian Estimation of the Additive Main Effects and Multiplicative Interaction (AMMI) Model,” Crop Science, 51, 1458–1469.
Gabriel, K. R. (1978), “Least Squares Approximation of Matrices by Additive and Multiplicative Models,” Journal of the Royal Statistical Society. Series B, Statistical Methodology, 40, 186–196.
Gauch, H. G. (1988), “Model Selection and Validation for Yield Trials With Interaction,” Biometrics, 44, 705–715.
Gelman, A., and Rubin, D. B. (1992), “Inference From Iterative Simulation Using Multiple Sequences,” Statistical Science, 7, 457–511.
Gollob, H. F. (1968), “A Statistical Model Which Combines Features of Factor Analytic and Analysis of Variance,” Psychometrika, 33, 73–115.
Han, C., and Carlin, B. P. (2001), “Markov Chain Monte Carlo Methods for Computing Bayes Factors: A Comparative Review,” Journal of the American Statistical Association, 96, 1122–1132.
Herz, C. S. (1955), “Bessel Functions of Matrix Argument,” Annals of Mathematics, 61, 474–523.
Hoff, P. D. (2009), “Simulation of the Matrix Bingham–von Mises–Fisher Distribution, With Applications to Multivariate and Relational Data,” Journal of Computational and Graphical Statistics, 18, 438–456.
James, A. T. (1964), “Distributions of Matrix Variates and Latent Roots Derived From Normal Samples,” Annals of Mathematical Statistics, 35, 475–501.
Jeffreys, H. (1961), Theory of Probability, Oxford: Clarendon Press.
Johnson, D. E., and Graybill, G. A. (1972), “An Analysis of a Two-Way Model With Interaction and No Replication,” Journal of the American Statistical Association, 67, 862–868.
Kass, R. E., and Raftery, A. (1995), “Bayesian Factors,” Journal of the American Statistical Association, 90, 773–795.
Kempton, R. A. (1984), “The Use of Biplots in Interpreting Variety by Environment Interactions,” Journal of Agriculture Science, 103, 123–135.
Khatri, C. G., and Mardia, K. V. (1977), “The von Mises–Fisher Matrix Distribution in Orientation Statistics,” Journal of the Royal Statistical Society. Series B. Methodological, 39 (1), 95–106.
Koev, P., and Edelman, A. (2006), “The Efficient Evaluation of the Hypergeometric Function of a Matrix Argument,” Mathematics of Computation, 75, 833–845.
Liu, G. (2001). “Bayesian Computation for General Linear–Bilinear Models,” Ph.D. dissertation, Department of Statistics, University of Kentucky, Lexington, KY.
Mandel, J. (1969), “The Partitioning of Interaction in Analysis of Variance,” Journal of Research of the National Bureau of Standards, Series B, 73, 309–328.
Mandel, J. (1971), “A New Analysis of Variance Models for Non-Additive Data,” Technometrics, 13, 1–18.
Marasinghe, M. G. (1985), “Asymptotic Tests and Monte Carlo Studies Associated With the Multiplicative Interaction Model,” Communications in Statistics. Theory and Methods, 14, 2219–2231.
Mardia, K. V., Kent, J. T., and Bibbi, J. B. (1979), Multivariate Analysis, London: Academic Press.
Raftery, A. E., and Lewis, S. M. (1995), “The Number of Iterations, Convergence Diagnostics and Generic Metropolis Algorithms,” in Practical Markov Chain Monte Carlo, eds. W. R. Gilks, D. J. Spiegelhalter, and S. Richardson, London: Chapman and Hall.
Schott, J. R. (1986), “A Note on the Critical Value in Stepwise Tests of Multiplicative Components of Interactions,” Communications in Statistics. Theory and Methods, 15, 1561–1570.
Seyedsadr, M. S., and Cornelius, P. L. (1992), “Shifted Multiplicative Models for Non-additive Two-Way Tables,” Communications in Statistics. Simulation and Computation, 21, 807–822.
Viele, K., and Srinivasan, C. (2000), “Parsimonious Estimation of Multiplicative Interaction in Analysis of Variance Using Kullback–Leibler Information,” Journal of Statistical Planning and Inference, 84, 201–219.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Perez-Elizalde, S., Jarquin, D. & Crossa, J. A General Bayesian Estimation Method of Linear–Bilinear Models Applied to Plant Breeding Trials With Genotype × Environment Interaction. JABES 17, 15–37 (2012). https://doi.org/10.1007/s13253-011-0063-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13253-011-0063-9