The exact zero-divisor graph of a reduced ring

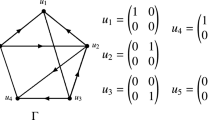
Abstract

The rings considered in this article are commutative with identity which are not integral domains. Let R be a ring. Recall that an element x of R is an exact zero-divisor if there exists a non-zero element y of R such that $Ann(x) = Ry$ and $Ann(y) = Rx$. As in Lalchandani (International J. Science Engineering and Management (IJSEM) 1(6): 14-17, 2016), for a ring R, we denote the set of all exact zero-divisors of R by EZ(R) and $EZ(R)\backslash \{0\}$ by $EZ(R)^{*}$. Let R be a ring. In the above mentioned article, Lalchandani introduced and studied the properties of a graph denoted by $E\Gamma (R)$, which is an undirected graph whose vertex set is $EZ(R)^{*}$ and distinct vertices x and y are adjacent in $E\Gamma (R)$ if and only if $Ann(x) = Ry$ and $Ann(y) = Rx$. Let R be a reduced ring such that $EZ(R)^{*}\ne \emptyset$. The aim of this article is to study the interplay between the graph-theoretic properties of $E\Gamma (R)$ and the ring-theoretic properties of R.