Abstract
Can the Spanish government generate more tax revenue by making personal income taxes more progressive? To answer this question, we build a life-cycle economy with uninsurable labor productivity risk and endogenous labor supply. Individuals face progressive taxes on labor and capital incomes and proportional taxes that capture social security, corporate income, and consumption taxes. Our answer is yes, but not much. A reform that increases labor income taxes for individuals who earn more than the mean labor income and reduces taxes for those who earn less than the mean labor income generates a small additional revenue. The revenue from labor income taxes is maximized at an effective marginal tax rate of 51.6% (38.9%) for the richest 1% (5%) of individuals, versus 46.3% (34.7%) in the benchmark economy. The increase in revenue from labor income taxes is only 0.82%, while the total tax revenue declines by 1.55%. The higher progressivity is associated with lower aggregate labor supply and capital. As a result, the government collects higher taxes from a smaller economy. The total tax revenue is higher if marginal taxes are raised only for the top earners. The increase, however, must be substantial and cover a large segment of top earners. The rise in tax collection from a 3 percentage points increase on the top 1% is just 0.09%. A 10 percentage points increase on the top 10% of earners (those who earn more than €41,699) raises total tax revenue by 2.81%.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
How much more tax revenue can the Spanish government generate by making income taxes more progressive? Three considerations motivate this question. First, the total tax collection constitutes a smaller fraction of Spanish GDP than other countries in the Euro Area (López-Rodríguez and García Ciria 2018). Table 1 documents different sources of tax revenue for Spain and Euro Area countries in 2015. The total tax collection with the personal income tax (PIT) is 7.2% of the GDP and 21.4% of total tax revenue in Spain. It represents the second largest source of tax revenue after the social security contributions. As a fraction of GDP, Spain collects around 2.3 percentage points less revenue from the PIT than the Euro Area countries, while its total tax collection is 4.8 percentage points lower.
Second, in all developed economies, economic booms are usually associated with reductions in taxes on personal income and, in particular, in the top marginal tax rates. In contrast, economic downturns are followed by tax increases (OECD 2019). Spain is not an exception. As Fig. 1 shows, with the high economic growth in the early 2000s, the top marginal tax rates were reduced by about 5 percentage points. This was reversed quickly with the 2008 financial crisis, and the top rates increased by more than 10 percentage points. Taxes were again reduced in the aftermath of the crisis.
Top marginal tax rates and GDP growth (%). Notes: This figure shows the evolution of the statutory marginal tax rates (left axis) and GDP growth (right axis). Note that there exists regional variation in top marginal rates. The figure depicts both the maximum and the minimum rates across regions. The source of GDP growth is the National Statistical Institute, see: https://bit.ly/345fXvG
Finally, there is an active public debate, both among academics and policymakers, on the most effective policies to address growing economic inequality. While many agree that there might be room for more redistribution and more extensive social programs, it is less clear whether higher progressivity of personal income taxes is the best way to generate the needed revenue (Blanchard and Rodrik 2019; Kopczuk 2019, and Saez and Zucman 2019). Since “the fundamental role of tax policy is to raise revenue to finance expenditures” (Kopczuk 2019), it is crucial to understand how much revenue can be raised by making taxes on personal income more progressive.
To understand the effects of tax progressivity on tax revenue, we build a life-cycle model with endogenous labor supply. In the model, individuals are born with permanent labor productivity differences. Each period they also face a persistent shock to their labor market productivity. These labor productivity shocks are not insurable. The combination of permanent differences and persistent shocks determine inequality among a given cohort of individuals as they age. In the face of labor productivity shocks, individuals try to smooth their consumption by adjusting their labor supply and savings. Labor and capital incomes are subject to separate progressive tax schedules. The progressivity of the labor income tax schedule provides insurance for individuals against unfavorable labor productivity shocks. The government also runs a means-tested transfer program, which provides another buffer against adverse productivity shocks. There is also an additional proportional tax on capital income, which captures the corporate income tax, and a proportional tax on consumption.
We calibrate the model economy to be consistent with both aggregate and cross-sectional targets for the Spanish economy. In particular, the model economy is able to generate distributions of labor income, total income (labor plus capital), and tax liabilities (who pays how much taxes) that are broadly in line with the microdata on tax returns. Furthermore, the model economy generates an elasticity of taxable income (ETI) that is in line with recent estimates by Almunia and Lopez-Rodriguez (2019).
In the benchmark economy, all individuals who earn more than about €11,000 pay labor income taxes according to \(t_{l}(I)=1-\lambda I^{-\tau },\) where I is labor income as multiples of mean labor income and \(t_{l}(I)\) is the average tax rate. The parameter \(\lambda \) determines the average taxes, while \(\tau \) determines the progressivity. If \(\tau =0\), \(t_{l}(I)=1-\lambda \), and everyone faces the same tax rate. When \(\tau >0\), individuals with higher incomes face a higher average tax rate. For the Spanish economy, \(\lambda =0.8919\) and \(\tau =0.1581\) provide a good description of labor income taxes (García-Miralles et al. 2019). With these parameters, individuals with mean labor income (€22,805 in 2015) face an average tax rate of 10.81% (\(1-\lambda \)). Their marginal tax rate is about 25%. The average (marginal) tax rate reaches about 36% (46%) for those who are at the top 1% of the labor income distribution (those who earn more than €94,974).
We consider two experiments that increase the progressivity of taxes on labor income. In the first experiment, we increase \(\tau \). This changes the entire tax schedule, so that all households below the mean labor income face lower average taxes, while those above the mean income face higher average taxes. Since with a higher \(\tau \), richer individuals face higher taxes, all else equal, the government collects more taxes. All else, however, is not equal since more progressive taxes lower incentives to work and save. As a result, a higher \(\tau \) might result in lower, not higher, revenue. The question is where the top of the Laffer curve is. We find that the tax revenue from labor income is maximized with \(\tau =0.19\). The increase in tax collection is, however, very small: The tax revenue from labor income increases only by 0.82% (or about 0.28% of the GDP).
The tax revenue from labor income is, however, only one part of the total tax collection. There are also taxes on capital and consumption. With \(\tau =0.19\), while the tax collection from labor income is maximized, the total tax collection declines by 1.55%. This happens since with a higher \(\tau \), the aggregate labor, capital, and output decline significantly. Indeed, the total tax collection falls for any increase in \(\tau \), and the level of \(\tau \) that maximizes total tax revenue is much lower, \(\tau =0.025\), than its benchmark value.
In the second experiment, we increase marginal tax rates for income above a threshold and keep taxes for the rest of the population intact. We experiment with higher marginal taxes on individuals who are at the top 1%, 5%, and 10% of the labor income distribution. For example, when we increase taxes on the top 1%, all individuals who earn more than €94,974 face a higher marginal tax rate on their incomes above this threshold. We consider increases in the marginal tax rates of 3, 5, and 10 percentage points.
We find that it is possible to generate higher total tax revenue by increasing taxes on the top earners. The increase in average tax rates, however, must be substantial. The additional tax collection from a 3 percentage points increase on the top 1% of earners, for example, is only 0.09%. Tax collection rises by 0.65% and 1.11% if a 3 percentage points tax increase is applied to individuals who are in the top 5% and 10% of the labor income distribution, respectively. The additional revenue is significantly higher when taxes are increased by 5 or 10 percentage points. With a 10 percentage points tax increase on the top 10% of earners (those who earn more than €41.699), for example, the total tax collection rises by 2.81%.
The main message of our quantitative exercises is that while it is possible to generate more tax revenue by making taxes more progressive, the extra revenue is not substantial. Higher progressivity has significant adverse effects on output and labor supply, which limits the room for collecting higher taxes. As a result, the only way to generate substantial revenue is with significant increases in marginal tax rates for a large group of top earners.
Related literature Our paper is related to two strands of the quantitative macro-literature that use parametric tax functions for optimal policy following the Ramsey (1927) approach.Footnote 1 The first is recent work on the Laffer curve in dynamic general equilibrium models, e.g., Trabandt and Uhlig (2011), Guner et al. (2016), Fève et al. (2018), İmrohoroğlu et al. (2018), and Holter et al. (2019). Trabandt and Uhlig (2011) study the Laffer curve in the one-sector growth model with infinitely lived representative agents. The others focus on environments with heterogeneous agents and uninsurable labor productivity risk.
Our approach follows Guner et al. (2016), who study the effect of higher progressivity on tax revenue for the USA and show that there is little room to raise revenue by making taxes more progressive. For the US economy, their benchmark parameters are \(\tau =0.053\) and \(\lambda =0.91\). They find that the tax collection from labor income is maximized at \(\tau =0.13\), with 6.8% additional revenue, while \(\tau =0.09\) would maximize the total tax revenue. They also show that the room to generate more significant revenue is smaller if average taxes (\(1-\lambda \)) are higher. We find that, for Spain, where the initial level of \(\tau \) and average taxes (\(1-\lambda \)) are higher, the extra revenue from a higher \(\tau \) is much smaller.
Holter et al. (2019), who use the same tax function specification, study a closely-related question: how the level of progressivity affects the ability of the government to collect more taxes from higher average taxes. They show that higher progressivity reduces the room to generate more revenue from higher average taxes. İmrohoroğlu et al. (2018) study optimal income taxation in a model with entrepreneurial activity. As in the current paper and Guner et al. (2016), they find that it is easier to raise extra revenue by taxing top earners.Footnote 2
The second strand is papers that study the welfare-maximizing degree of tax progressivity. Earlier papers in this literature include Ventura (1999), Bénabou (2002), Caucutt et al. (2003), Conesa and Krueger (2006), Erosa and Koreshkova (2007), and Conesa and Krueger (2009). After Diamond and Saez (2011), who suggest that the optimal marginal tax rate on the top 1% of earners should be 73%, several papers focused on the optimal taxes on top earners, e.g., İmrohoroğlu et al. (2018), Kindermann and Krueger (2018), Badel et al. (forthcoming), and Brüggemann (2019). Among them, Badel et al. (forthcoming) focus on the role of human capital accumulation, while İmrohoroğlu et al. (2018) and Brüggemann (2019) study the role of entrepreneurs.
Heathcote et al. (2017), Storesletten (2019), and Serrano-Puente (2020) study optimal progressivity with the same tax function used in this study and look for the welfare-maximizing level of \(\tau \). Among these, in a paper simultaneous to ours, Serrano-Puente (2020) studies the optimal progressivity of personal income taxes in Spain. He finds that the welfare-maximizing level of \(\tau \) is 0.15. Heathcote et al. (2017), in a model with both insurable and uninsurable risk and human capital accumulation, find that a utilitarian planner would set \(\tau =0.084\) for the US economy, a value close to the level of \(\tau \) in Guner et al. (2016) that maximizes the total tax collection. Storesletten (2019) asks how the optimal \(\tau \) should change with the underlying income inequality. He finds that \(\tau \) should be higher in the USA today than it was in 1980, while the measured \(\tau \) declined during this period.Footnote 3
Two key intuitions on the optimal level of progressivity emerge from these two strands of the literature. First, the revenue or welfare-maximizing level of progressivity depends critically on the nature of labor productivity shocks at the top of the income distribution. If being a top earner is a relatively transitory state (e.g., in Kindermann and Krueger (2018)), then it is optimal to tax top earners at a high rate, since their labor supply reaction will be limited. On the other hand, if being a top earner is a relatively permanent state (e.g., in Guner et al. (2016)) or requires human capital accumulation (e.g., in Heathcote et al. (2017) and Badel et al. (forthcoming)), there is less room to increase taxes at the top. Second, the tax base matters. If progressive taxes are applied only to labor income (e.g., in Kindermann and Krueger (2018)), then the optimal taxes on top earners are high. The taxes at the top are lower if both labor and capital incomes are taxed jointly (e.g., in Guner et al. (2016) and İmrohoroğlu et al. (2018)). In the current paper, being a top earner is a relatively permanent state, while progressive taxes are primarily applied to labor income.
The paper is organized as follows: In Sect. 2, we describe the main characteristics of the Spanish tax system. In Sect. 3, we lay out the life-cycle model that defines the benchmark economy. The calibration of the model is discussed in Sect. 4. We describe our main results in Sect. 5. Finally, Sect. 6 concludes.
2 The Spanish tax structure
In this section, we provide a brief overview of the Spanish personal income tax. We focus on 2015, the latest year for which microdata on tax returns is available. We also present estimates of effective tax functions that describe taxes paid on labor and capital income in a parsimonious way, and an effective tax-credit function. A more extended discussion can be found in García-Miralles et al. (2019). The Spanish tax system raises revenue from taxes on the income, consumption and wealth of individuals, and on profits of firms. Total tax collection was 33.6% of GDP in 2015, which was close to the OECD average (33.7%), but significantly less than the Euro-11 average (38.4%).Footnote 4 The primary source of revenue is social security contributions, which take the form of a payroll tax.Footnote 5 Individual income, both from labor and capital, is also taxed through a progressive personal income tax. Taxes on goods and services include a three-notch value-added tax and excise duties on specific goods such as fuel, electricity, tobacco, and alcohol. Firm profits are taxed through the corporate income tax.Footnote 6 Finally, some taxes are levied on the use, ownership, and transmission of assets, such as a real-estate tax, a wealth tax, inheritance and gift tax, and taxes on the transfer of real estate and other financial assets.Footnote 7 Social security contributions account for 33.5% of total tax revenue, while the personal income tax accounts for 21.4%. The share of the value-added tax, excise duties, the corporate income tax, and taxes related to the use, ownership, and transmission of assets are 19.0%, 8.6%, 7.1%, and 7.6%, respectively.Footnote 8
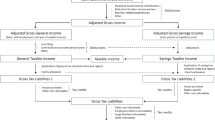
Income subject to the personal income tax, which is the main focus of this paper, consists of labor income, self-employment income, and different types of capital income. The personal income tax code classifies these income categories into two groups, which are subsequently taxed at different rates. General income includes labor income, self-employment income, and some forms of capital income (mainly real-estate income). Savings income comprises the main portion of capital income, e.g., realized capital gains, dividend payments, and interest income. Below we refer to general income simply as labor income and savings income as capital income.
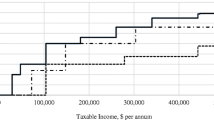
The tax schedule for labor income is highly progressive. The exact schedule depends on the taxpayer’s region and consists of between 5 and 14 tax brackets, with a top marginal rate ranging from 43.5% to 48%.Footnote 9 The capital income tax schedule is much less progressive and does not differ across regions. The number of tax brackets is three, and the top rate is 23.5%. The left-hand side of Fig. 2 shows the labor income tax schedules of the two largest regions by GDP (Madrid and Catalonia). The right-hand side shows the tax schedule on capital income.
Statutory marginal tax rates (2015). Notes: This figure shows the statutory marginal tax rates of the personal income tax in 2015 for residents in Catalonia and Madrid, the two largest Spanish regions by GDP. Panel A displays the rates applied to labor (general) income. Panel B shows the tax rates on capital (savings) income
The personal income tax also features a wide range of tax benefits that reduce tax liabilities. There are two types of benefits: deductions, which reduce the tax base (i.e., they apply to income before tax liabilities are calculated), and credits, which reduce the tax liabilities (i.e., they apply directly to tax liabilities). Examples of tax deductions are the part of social security contributions paid by the employee, a deduction for earning any labor income, business expenses associated with self-employment, a deduction for couples filing jointly, and contributions to private pension plans. Tax credits include a family allowance, which depends on the characteristics of the taxpayer and her family, such as age or number of dependent relatives, benefits granted for mortgage payments, and tax credits for employed mothers with children below age three.Footnote 10
We follow García-Miralles et al. (2019) and represent income taxes and credits with three functions. The first function, whose formulation is used, among others by Bénabou (2002), Guner et al. (2016), and Heathcote et al. (2017), applies to labor income:
where \(t_l\) is the average tax rate on labor income, \(I_l\) stands for multiples of mean labor income, and \(\widetilde{I}_l\) is an income threshold below which the labor income tax is zero. The income threshold accounts for the fact that a large share of taxpayers at the low end of the income distribution face a zero tax rate. Total tax liabilities from the labor income tax are then given by \(T_l(I_l) = t_l(I_l)\cdot I_l\cdot \bar{I}_l\), where \(\bar{I}_l\) is mean labor income (€22,805 in 2015).
The second function captures the savings tax schedule and applies to capital income:
where \(t_k\) is the average tax rate on capital income, \(I_k\) stands for multiples of mean capital income, \(\kappa \) is the capital income tax rate if \(I_k\ge \widetilde{I}_k\) and \(\widetilde{I}_k\) is a capital income threshold that provides a kink in the function. Total tax liabilities from the capital income tax are given by \(T_k(I_k) = t_k(I_k) \cdot I_k \cdot \bar{I_k}\), where \(\bar{I_k}\) is mean capital income (€1,486 in 2015).
Finally, tax credits are given by the following formula:
where the term in brackets is the level of tax credits as a fraction of individual (labor and capital) income; I stands for multiples of mean total income, and \(\bar{I}\) is mean total income (€24,291 in 2015).
Figure 3 depicts the effective taxes on labor and capital income and tax credits.Footnote 11 An individual with mean labor income faces an average tax rate of about 10%. The average tax rate reaches about 35% for a labor income that is seven times the mean (€159,635 in 2015). The average tax rate on capital income starts at 12.72%. It increases slowly, reaches 20.18% for a capital income that is about 13 times the mean capital income (€19,318 in 2015), and stays at that level afterward. Finally, the tax credits have a steep-hump shape. They start at 0.85% of gross income, reach a maximum of about 1.8% of gross income at around 80% of mean income (€19,433) and then decline quickly to the initial level by around twice mean income (€48,582). Table 2 shows the parameter values.
Parametric functions of the personal income tax. Notes: This figure plots the estimation of the three parametric tax functions of the Spanish personal income tax, namely the average general tax rate, which is applied to labor income in the model (panel A), the average savings tax rate, which is applied to capital income (panel B) and tax credits as a fraction of gross income (panel C). The parametric estimates of each function are borrowed from García-Miralles et al. (2019). Each data point corresponds to the mean average tax rate (panels A and B) or tax credit (panel C) of taxpayers whose income is larger than or equal to the point in the x-axis and less than the next point. For the last point, i.e., 9.8 (panels A and C) and 20 (panel B), the data are calculated for incomes between 9.8 and 10.2 and between 20 and 21 of mean income, respectively
3 Model
The model follows Guner et al. (2016). Consider a standard incomplete markets stationary life-cycle economy with endogenous labor supply. The model period is one year. We index age by j. Each period a continuum of agents is born. Agents live a maximum of J periods and face a probability \(s_{j}\) of surviving up to age j conditional upon being alive at age \(j-1\). The population grows at a constant rate n. The demographic structure is stationary, such that age—j agents constitute a fraction \(\mu _{j}\) of the population at any point in time. The weights \(\mu _{j}\) are normalized to sum to 1 and are given by the recursion \(\mu _{j+1}=(s_{j+1}/(1+n))\mu _{j}\). Individuals retire at age \(J_{R}.\)
Individuals are born with a given labor productivity level (a permanent shock) and receive a persistent shock to labor productivity each period. Individuals can smooth these shocks by adjusting their labor supply. They also have access to a risk-free asset, which is priced by a representative firm with a constant return to scale production technology. Individuals are born with no assets.
A government taxes individuals and provides means-tested transfers. There are four taxes: a progressive tax on labor income, another progressive tax on capital income, a flat tax on consumption, and an additional flat tax rate on capital income. The proportional tax on capital income captures the corporate income tax. Individuals also pay a proportional labor income tax to finance a pay-as-you-go social security system. Individuals receive two types of transfers from the government: nonlinear tax credits, which reduce their tax liability, and means-tested transfers, which provide direct income support for poor individuals.
Individuals have preferences over streams of consumption and hours worked and maximize:
where \(c_{j}\) and \(l_{j}\) denote the consumption and labor and the parameter \(\gamma \) is the Frisch elasticity of labor supply. The parameter \(\varphi \) controls the disutility from work.
There is a constant returns to scale production technology that transforms capital K and effective labor L into output Y:
The capital stock depreciates at rate \(\delta \). Let w and r be the market wage and interest rate, which are pinned down by the FOCs from firms’ profit maximization problem.
3.1 Labor productivity shocks
Following Storesletten et al. (2004) and Kaplan (2012), the labor market productivity of an age-j individual is given by
where
where \(\overline{e}_{j}\) is a non-stochastic labor productivity profile, which is common to all individuals, \(\theta \) is an individual-specific permanent shock, and \(z_{j}\) is a persistent, AR(1), shock. We assume that \(\eta _{j}\sim N(0,\sigma _{\eta }^{2})\).
For the permanent shock (\(\theta \)), we assume that a fraction \(\overline{\pi }\) (\(\underline{\pi }\)) of the population is endowed with \(\overline{\theta }\) (\(\underline{\theta }\)) at the start of their lives, whereas the remaining \((1-\overline{\pi }-\underline{\pi })\) fraction draws \(\theta \) from \(N(0,\sigma _{\theta }^{2}).\) The parameters \(\overline{\pi }\) and \(\underline{\pi }\) capture individuals who are at the top and bottom of the income distribution.Footnote 12 Let \(\Omega =\{\theta ,z\}\), with \(\Omega \in \mathbf {\Omega }\), \(\mathbf {\Omega } \subset \mathfrak {R}^{2}\). We represent the market return per hour of labor supplied of an age-j individual by \(we(\Omega ,j)\), where \(e(\Omega ,j)\) is a function that summarizes the combined productivity effects of age and idiosyncratic productivity shocks. Individuals who are retired have \(e(\Omega ,j)=0\) and receive a social security payment b.
3.2 Taxes and transfers
Consider an age-j individual who earns labor income \(I_{l}=we(\Omega ,j)l_{j}\) and capital income \(I_{k}={ra_{j}}\). Let \(I=I_{l}+I_{k}\). Individuals face a labor tax schedule, \(T_{l}\), and a capital tax schedule \(T_{k}\), which are increasing and convex functions. They also face a proportional labor tax, \(\tau _{ss}\), that finances the social security system, and a proportional capital tax, \(\tau _{k}\). Let
denote the total tax payments on individual income.Footnote 13 The individuals also face a proportional tax on their consumption, \(\tau _{c}\).
Individuals receive two types of transfers, tax credits, \(TR_{c}(I)\), and means-tested transfers, \(TR_{m}(I)\). Hence, the total transfers are given by
Each period, the government consumes G, which is financed by the net tax revenue. We assume that the social security budget is balanced each period. We also assume that all unintended bequests are fully taxed by the government.
3.3 Decision problem
The dynamic programming problem of an age-j individual is then given by
subject to
where
with
We provide a formal definition of equilibrium in Appendix A.
4 The benchmark economy
4.1 Calibration
Individuals start their life at age 25 and retire at age 65 \((J_{R}=40)\). All individuals die with certainty at age 100 (\(J=75)\). To characterize the labor market productivity of an age-j individual, we first estimate \(\overline{e}_{j}\), the non-stochastic age-productivity profile. Let \(w_{j,t}\) be the mean hourly wage rate for individuals of age j at time t, and consider the following regression
where \(D_{j}\) and \(D_{t}\) are age and time dummies. The non-stochastic age-productivity profile, \(\overline{e}_{j},\) is given by \(D_{j}\). To estimate Equation (8), we use data from 2004-2012 European Union Statistics on Income and Living Conditions (EU-SILC). Further details are provided in Appendix B.1.
Seven other parameters characterize the labor market productivity: \(\sigma _\theta ^2\) (the variance of the permanent shock), \(\sigma _\eta ^2\) (the variance of innovations to the persistent shock), \(\rho \) (the autocorrelation coefficient for the persistent shock), \(\underline{\pi }\), \(\overline{\pi }\), \(\underline{\theta }\) and \(\overline{\theta }\) (the fraction of individuals with high and low permanent shocks and the levels of these shocks). We calibrate these parameters in two steps. First, we choose \(\sigma _{\theta }^{2},\sigma _{\eta }^{2}\) and \(\rho ,\) such that the variance of log wages implied by Equation (6) is consistent with the data. To estimate the variance of log wages in the data, we use an equation like (8) with the variance of log wages as the dependent variable. We then simulate a large number of individuals whose wages are determined by Equation (6) and choose \(\sigma _\theta ^2, \sigma _\eta ^2\), and \(\rho \) to minimize the distance between data and model-generated age profiles of the variance of log wages. We again delegate the details to Appendix B.2.
In the second step, we set \(\underline{\pi }=0.1\) and \(\overline{\pi }=0.01\), i.e., the bottom 10% and the top 1% of the population, and given \(\sigma _\theta ^2, \sigma _\eta ^2\), and \(\rho \) values, choose \(\underline{\theta }\) and \(\overline{\theta }\) so that the model economy matches the fraction of labor income earned by the bottom 10% and the top 1% of individuals in the data. This procedure generates \(\underline{\theta }=-2.12\) and \(\overline{\theta }=2.005\). Hence, the bottom 10% and the top 1% have permanent shocks that are exp\((-2.12)=0.12\) and exp\((2.005)=7.43\) times the median productivity of individuals who are in the middle 89% of the population, respectively.
For preferences, we set the Frisch elasticity of labor supply, \(\gamma \), to 0.5. The early estimates of \(\gamma \), such as MaCurdy (1981) and Altonji (1986), were much smaller. There has emerged, however, a consensus that these early estimates were biased downward and a value around or above 0.5 is reasonable (Imai and Keane 2004; Domeij and Flodén 2006; Chetty 2012; Keane and Rogerson 2015). We set the parameter \(\varphi \) to match mean hours of work and \(\beta \) to match the capital to output ratio. In 2015, the annual average hours worked per worker was 1,700, or 0.34 when normalized by 5,000 available hours in a year.Footnote 14 For the same year, we calculate the capital-output ratio, K/Y, to be 3. For this calculation, the nominal capital stock is taken from the Capital Input File by EU-KLEMS (variable K_GFCF) and the nominal GDP is taken from the National Accounts published by the National Statistical Institute (INE).Footnote 15 The survival rates are calculated from the 2013 Spanish Life Tables published by the INE.Footnote 16 Given the low population growth rate in Spain, we set \(n=0.\)Footnote 17
We calculate the capital share, \(\alpha \), from the EU-KLEMS Basic File by dividing the capital compensation (the variable is named CAP) over the gross value added (variable VA). For 2015, the calculated value is 0.397. We then choose \(\delta =0.07\) such that the model economy matches the investment-to-output ratio. The investment-to-output ratio, I/Y, is computed as the fixed gross capital formation over GDP, where both figures are taken from the National Accounts. We use the average value for 2010-2015, 20.6%, as the target.
We are then left with parameters that determine the tax and the transfer system. For labor income taxes \(T_{l}(.)\), capital income taxes \(T_{k}(.)\), and tax credits \(T_{c}(.)\), we use the estimates from Table 2 in Sect. 2. For means-tested transfers, \(TR_{m}(.)\), we follow Guner et al. (2019), who estimate a linear transfer function,
where \(\overline{I}\) is mean income. Hence, an individual with zero income receives \(g_{0}\), which is about 4% of mean income in the economy. If an individual has positive income, she faces a schedule that starts from a lower initial point \((g_{1}=0.024)\) and transfers decline by income (\(g_{2}=-0.01)\). Individuals with incomes higher than 2.4 times the mean income (€58,298 in 2015) do not receive any transfers.Footnote 18
Bover et al. (2017) estimate effective taxes on consumption by income deciles. Their estimates show that the tax rate on consumption varies very little by income and is about 15%. Hence, we set \(\tau _{c}=0.15\). We choose \(\tau _{k}\) to match the collection of the corporate income tax, which is about 2.4% of GDP in the data.Footnote 19 Finally, we set b to reproduce a replacement rate of 59.7%, and set \(\tau _{ss}=30\%\) to balance the social security budget. We define the replacement rate in the data as the ratio of payments to new beneficiaries over average earnings in 2015. The average yearly social security income of new beneficiaries was €14,686 (€1,049 for 14 months) in 2015,Footnote 20 and average earnings was €24,593.6.Footnote 21
Table 3 shows the parameter values.
4.2 Model fit
Table 4 shows the cross-sectional inequality of labor and total income in the model and the data. The data on incomes and taxes paid come from the administrative sample of tax returns that is used to estimate effective tax and tax-credit functions. We use the share of labor income by the bottom 10% and the top 1% of taxpayers as targets to discipline \(\underline{\theta }\) and \(\overline{\theta }\). The model also does a good job matching the other moments of the labor income distribution. The share of the bottom quintile is 4.2% in the data and 5.4% in the model. The share increases sharply for higher quintiles, and the top quintile has an income share of 44.9% in the data and 41.4% in the model. The model is also able to generate the share of labor income accounted for by higher percentiles. The share accounted for by the top 5% earners in the data is about 17.6%, while the model generates 17.2%. Table 4 also reports a few aggregate measures of income inequality. The model does a good job generating 90/10, 50/10, and 90/50 percentile ratios, that are pretty much in line with the data. On the other hand, the Gini index, which is more sensitive to the middle of the income distribution, where most observations are, is smaller in the model than it is in the data.
What about the distribution of total gross (pre-tax) income? As Table 4 (columns 3 and 4) shows, the model is not able to generate the concentration of gross income at the very top of the income distribution. The top 10% of individuals have 31.5% of gross income in the data. The model counterpart is 25.8%. The difference, about 5 percentage points, is almost entirely accounted for by the lower share of gross income by the top 1%. In contrast, the individuals at the bottom of the income distribution in the model have a higher share of gross income than they do in the data. The first quintile, for example, has an income share of 8.1% in the model, in contrast to 4.6% in the data. Since we match the distribution of labor income pretty well, the gap is due to lower saving rates and capital income at the top of the income distribution. This is not surprising since the model abstracts from several features that are found to be important in the literature to generate a higher concentration of capital income at the top of the income distribution, such as bequests or entrepreneurs (see De Nardi et al. (2017) for a review of the literature).Footnote 22
In Table 5, we show how well the model matches the distribution of taxes paid. As far as income tax liabilities are concerned, i.e., the taxes on capital and labor income minus tax credits (\(T_{l}(.)+T_{k}(.)-T_{c}(.)\)), the parsimonious representation of the tax system in the model is able to generate a distribution that is in line with the data. Both in the data and the model, the distribution of tax payments is more concentrated than the distribution of total income. The first and second income quintiles do not pay any taxes in the data, while the top income quintile accounts for about 73.2% of tax payments. The shares of the top 10% and the richest 1% are 55% and 21% of tax payments, respectively. The model outcomes are broadly consistent with this pattern: The bottom quintile pays only 2% of taxes, while the top quintile generates about 65% of tax payments. The share of the top 10% in total tax revenue is about 45% in the model. The model generates a lower concentration of taxes paid at the top, which simply reflects the lower gross income share of the top 1%. In the benchmark economy, the total tax collection, including social security taxes, is about 35% of the GDP.
Table 5 also shows the distribution of consumption taxes. Consumption tax liabilities are much more equally distributed than income tax liabilities. The bottom quintile pays about 9% of consumption taxes in the data, while the top quintile’s share is 34.2%. The share is only 2.4% for the top 1%. The model does a very good job generating this pattern, which results from a proportional tax on consumption coupled with the fact that the consumption to income ratio is lower for the richer households.
5 The tax reforms
How much more tax revenue can the Spanish Government generate by making taxes more or less progressive? In this section, we answer this question by comparing counterfactual economies that have a higher or lower progressivity than the benchmark economy. We focus on the progressivity of taxes on labor income.
The parameter \(\tau \) in the labor tax function \(t_{l}(I_{l})=1-\lambda (I_{l})^{-\tau }\) controls the progressivity of taxes. As we have already noted, when \(\tau =0\), taxes are proportional and all individuals have the same average tax rate, \(t_{l}(I_{l})=1-\lambda \). When \(\tau >0\), the average tax rate is increasing in \(I_{l}\), as in Fig. 3. Furthermore, with \(\tau >0\), taxes are progressive, i.e., marginal tax rates are higher than the average ones. For this tax function, the marginal tax rate is given by \(m_{l}(I_{l})=\frac{\partial T(I_{l})}{\partial I_{l}}=1-\lambda (1-\tau )I_{l}^{-\tau }\). Then,
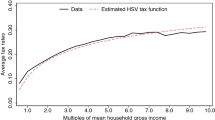
We report how tax revenue and other aggregate outcomes, such as capital, labor, and output, change across steady states for different values of \(\tau \). The other parameters of the tax system are kept at their benchmark values. The middle panel of Table 6 reports tax collection from labor income taxes, i.e., taxes collected from schedule \(T_{l}(.)\), and total taxes collected, i.e., \(T_{l}(.)+T_{k}(.)-T_{c}(.)\) plus tax collection from the proportional taxes on capital (\(\tau _{k})\) and consumption (\(\tau _{c})\). For each outcome, we normalize the benchmark value, with \(\tau =0.1581\), to 100. Figure 4 shows the tax revenue as a function of \(\tau ,\) the Laffer curve.
Tax progressivity and tax collection. Notes: This figure shows the tax collection from labor income and the total tax collection as a function of the progressivity of the labor income tax function. The variables are normalized to 100 at the benchmark value of progressivity (\(\tau =0.1581\)). This value and those corresponding to the top of the total and labor income tax curves are marked with vertical lines
As Table 6 shows, it is possible to generate higher tax collection from labor income by increasing \(\tau \). The additional tax revenue is, however, small. The top of the Laffer curve is reached when \(\tau =0.19\), where the increase in tax revenue from labor income is only 0.82%. Figure 5 shows average tax rates implied by \(t_{l}(I_{l})=1-\lambda (I_{l})^{-\tau }\) for \(\tau =0.1581\) (the benchmark value), and \(\tau =0.19\) (the value that maximizes the tax revenue from labor income). The income levels in Fig. 5 are reported as multiples of mean labor income, \(\overline{I}_{l}\). A higher value of \(\tau \) rotates the tax function around \(I_{l}=\overline{I}_{l}\), i.e., when \(\tau \) increases individuals who earn more than \(\overline{I}_{l}\) (€22,805 in 2015) pay higher taxes, while individuals who earn less than \(\overline{I}_{l}\) pay lower taxes. In 2015, this would imply higher average taxes for 38% of taxpayers. Table 7 shows how average and marginal tax rates change with \(\tau \) at the top of the income distribution. In the benchmark economy, individuals who are at the top 1% of the income distribution face an average tax rate of 36.2%. Their marginal tax rate is 46.3%. With \(\tau =0.19\), the marginal tax rate for the top 1% increases to 51.6%, an increase of about 5 percentage points. The taxes also increase for those who are at the top 5% and 10% of the income distribution, although increases are smaller.
The upper panel of Table 6 shows that capital, effective labor, and output decline monotonically with \(\tau \). Hence, as the economy moves from \(\tau =0.1581\) to \(\tau =0.19\), the government is collecting higher taxes from labor, but the aggregate labor supply and output decline. For \(\tau \) higher than 0.19, the decline in labor supply dominates and tax collection from labor income is lower. For values smaller than \(\tau =0.19\), while the economy has higher labor supply and output, the lower tax rates on high incomes result in a smaller tax collection. Table 6 also shows how the labor supply of individuals in the top 1% of the income distribution changes. The labor supply of the top 1% reacts quite strongly to tax changes. In particular, with \(\tau =0.19\), their labor supply declines by more than 5%.
Since higher values of \(\tau \) are associated with lower levels of capital, labor, and output, at \(\tau =0.19\), the total tax collection is 1.55% lower than the benchmark economy. The level of \(\tau \) that maximizes the total tax collection is 0.025, which implies significantly less progressive taxes than in the benchmark economy. As Fig. 5 and Table 7 show, at \(\tau =0.025\), the top earners face lower taxes, while individuals whose income is lower than the mean labor income face higher taxes. The average tax rate for the top 1% of earners is 15.5%, which is almost 20 percentage points lower than the benchmark economy. In the economy with \(\tau =0.025\), the aggregate capital, labor, and output increase significantly. The steady-state output, for example, is almost 11 percentage points higher than the benchmark economy. As a result, the government is able to collect higher taxes despite lowering taxes on the top earners. Indeed, the total tax collection (including social security taxes) as a fraction of GDP declines by 5.1% with \(\tau =0.025\).
Finally, the lower panel of Table 6 documents how income inequality changes. Not surprisingly, the inequality is higher (lower) with lower (higher) progressivity. At \(\tau =0.025,\) which maximizes the tax collection from total income, the Gini index increases from 0.32 to 0.34, while 90/10 percentile ratio increases from 6.99 to 8.02.Footnote 23
The relationship between tax progressivity and tax revenue depends critically on the Frisch elasticity of labor supply. Higher (lower) values of \(\gamma \) will generate smaller (or larger) additional revenue from higher progressivity, since with a higher (lower) \(\gamma \) labor supply will react more (less) to tax changes. In Appendix F, we present results for \(\gamma =1\). We find that in an economy recalibrated to match the same set of targets, the benchmark value of \(\tau =0.1581\) generates the maximum revenue from the labor income tax, i.e., there is no room to make taxes more progressive and collect higher taxes from labor income. Furthermore, total tax collection is maximized when \(\tau =0\), i.e., when taxes are proportional.
5.1 Elasticity of taxable income
In this section, we calculate the elasticity of taxable income (ETI) associated with changes in \(\tau \). To this end, let \(x=(a,\Omega )\) be the state and \(I(x,\tau )\) be the income of an individual with x under \(\tau \). Given a measure of individuals over x in an economy characterized by \(\tau \), call it \(\psi (x,\tau )\), the ETI can be calculated as
where \(m(x,\tau )\) is the marginal tax rate of individual in state x when labor taxes are characterized by \(\tau \), and \(1-m(x,\tau )\) is the net-of-tax rate.
Basically, the ETI measures how much income, labor income or total income, changes when marginal taxes change because of a higher or lower \(\tau \). In the model, the ETI is simply a summary measure of how incomes change due to labor supply and savings responses. In the data, on the other hand, the ETI measures labor supply and savings responses as well as any changes in tax avoidance or tax shifting between different income sources, and it is a challenging object to measure.Footnote 24
We calculate the ETI when the economy moves from \(\tau =0.1581\) (the benchmark value) to \(\tau =0.19\) (the value that maximizes the tax collection from labor income). We find that the ETI is 0.45 for both labor and total income. Almunia and Lopez-Rodriguez (2019) estimate the ETI for Spain by exploiting three large reforms to the Spanish personal income tax that took place between 1999 and 2014. Their most reliable estimates of the ETI are between 0.45 and 0.64. The model estimates are within this range, which provides further support for \(\gamma =0.5\) as a reasonable benchmark value. It is also assuring that the model estimates are closer to their lower-bound estimates, since the model only allows for labor supply and saving responses to tax changes.
5.2 Higher taxes only for the top incomes
As Fig. 5 illustrates, changes in \(\tau \) rotate the entire tax function around \(\overline{I}_{l}\) and average taxes increase or decrease for everyone. The public debate on tax progressivity, on the other hand, focuses on increasing taxes on top incomes without changes in other parts of the tax function. In this section, we study the effects of higher taxes on the top earners. In particular, we increase the marginal taxes on labor income by x percentage points for all labor income above a certain threshold. We consider the labor income thresholds that define the top 1, 5 and 10% of the labor income distribution in the benchmark economy. Hence, labor income tax liabilities \(T_{l}(I_{l})\) become

where the new threshold, \(\widehat{I}_{l}\) (in multiples of the mean labor income), is the income level that defines the top 1, 5 or 10% of the labor income distribution in the benchmark economy.Footnote 25 In 2015, these thresholds were €94,974, €53,778 and €41,699. We evaluate increases in the marginal tax rates by 3, 5 and 10 percentage points. We again focus on steady-state comparisons and keep the other features of the tax system intact.
Table 8 shows the results. In contrast to experiments with a higher \(\tau \), it is possible to increase the total tax collection by increasing marginal tax rates on the top earners. Yet, the tax hike has to be substantial to generate significant effects on tax collection. The rise in tax collection with a 3 percentage points increase on the top 1% of earners, for example, is only 0.09%.Footnote 26 Tax collection increases by 0.65% and 1.11% if a 3 percentage points tax increase is applied to individuals who are in the top 5% and 10% of the labor income distribution, respectively. The additional revenue is significantly higher when taxes are increased by 5 or 10 percentage points. With a 10 percentage points tax increase on the top 10% of earners, for example, the total tax collection increases by 2.81%.Footnote 27,Footnote 28
To put these experiments in perspective, we next evaluate a proposal by the new coalition government formed in early 2020.Footnote 29 The proposal increases the marginal labor income tax, \(t_{l}(I_{l})\), by 2 percentage points for people who earn above €130,000 and 4 percentage points for people with earnings above €300,000. It also increases the marginal capital income tax, \(t_{k}(I_{k})\), by 4 percentage points for all capital incomes above a capital income threshold of €140,000. Hence, with this reform total taxes on labor income, \(T_{l}(I_{l})\), will look like Equation (10) but with two, rather than one, thresholds. Similarly, total taxes on capital income will be given by \(T_{k}(I_{k})=\kappa \cdot I_{k}\cdot \overline{I}_{k}+x(I_{k}-\widehat{I}_{k})\cdot \overline{I}_{k}\), where \(\widehat{I}_{k}\) is the capital income threshold (in multiples of the mean capital income) for €140,000 in the model.
The labor income thresholds in this experiment, €130,000 and €300,000, are much higher than the income thresholds we have considered in the reforms reported in Table 8. The threshold that defines the top 1% of the labor income distribution, for example, is only €94,974. As a result, compared to Table 8, a much smaller fraction of individuals would pay higher labor taxes with this reform. In 2015, only 0.4% of taxpayers in Spain had a reported labor income above €130,000, while the fraction who earned more than €300,000 was just 0.07%. Similarly, only 0.1% of taxpayers had a reported capital income above €140,000.Footnote 30 As a result, the additional total tax collection from this reform is very small. The total tax collection increases only by 0.12%.Footnote 31
6 Conclusions
We study how much revenue can be generated by increasing the progressivity of the personal income tax in Spain. It is possible to increase the total tax collection by increasing marginal taxes on top earners. The increase in taxes, however, has to be substantial and apply to a broad group. The rise in tax revenue from a small, e.g., 3 percentage points, increase for the top 1% is minimal (0.09%). More significant additional revenue can be generated by increasing marginal taxes for the top 10% of earners (those that earned more than €41,699 in 2015). A 10 percentage points increase, for example, generates 2.81% higher revenue. A 10 percentage points increase in the marginal tax rate for such a large group is, however, a fundamental change of the current tax system.
We conclude with three caveats: First, we abstract from capital income risk that can be important to generate a more realistic wealth distribution. We also limit our analysis to personal income taxes, leaving aside potential gains from a more efficient taxation of corporate incomes (Erosa and González 2019).
Second, the analysis above focuses on the effects of tax progressivity on government revenue. A separate question is whether a higher or lower progressivity is optimal from a welfare point of view. A higher progressivity, e.g., higher \(\tau \), increases tax liabilities of rich households and lowers tax liabilities of the poor ones. Given the concavity of the utility function, this would increase aggregate welfare since after-tax income, and, as a result, consumption, will be higher for households with higher marginal utility. A higher progressivity also provides better insurance for individuals against adverse labor market productivity shocks. These potential welfare gains, however, have to be weighed against the negative effects of a higher \(\tau \) on labor supply and capital accumulation. Serrano-Puente (2020) studies the optimal progressivity of taxes in Spain. He considers an economy where total (labor plus capital) income is subject to the tax function \(t(I)=1-\lambda I^{-\tau }\) with a benchmark value of \(\tau =0.1224\). He finds that \(\tau =0.15\) maximizes the steady-state welfare.
Third, the analysis above abstracts from transitional dynamics. When a change in \(\tau \) is introduced, it will take a while for the capital stock to decline to its new steady-state value. Indeed, as highlighted by Guner et al. (2016), in the very first period, the capital stock is fixed and there could be a more substantial rise in government revenue.
Notes
Another strand of literature follows Mirrlees (1971), who characterizes optimal income taxes without imposing any constraints on the shape of the tax schedule. Diamond (1998) and Saez (2001) are more recent contributions in static models, while Farhi and Werning (2013), Golosov et al. (2016), and Heathcote and Tsujiyama (2019) extend the analysis to dynamic environments.
A related question is how the effects of tax changes depend on the underlying income and wealth inequality. For the USA, Macnamara et al. (2020) show that the impact of tax policies is more significant in a 1983-economy (with lower income and wealth inequality) than they are today.
The source is the OECD Tax Statistics, available at https://doi.org/10.1787/tax-data-en.
The payroll tax applies to monthly earnings, up to a ceiling of €4070. The tax rate is 36.25% and consists of three parts: a 28.3% tax (23.6% by employers and 4.7% by workers) to finance the social security payments, a 7.25% tax (5.7% by employers and 1.55% by workers) to fund unemployment benefits and severance payments, and a 0.7% tax (0.6% by employers and 0.1% by workers) to fund training programs.
The corporate income tax is proportional, the rate being 25%. There is, however, some heterogeneity. For instance, new firms pay a lower rate (15%), while banks face a higher tax (30%).
In terms of tax revenue, the most significant is the real-estate tax, which applies to the ownership of any real estate. Next is the transfer and stamp tax, which taxes, among other activities, the purchase and sale of real estate, and the inheritance and gift tax. The wealth tax raises relatively little revenue since it only applies to wealth beyond a high threshold, and it is zero in some regions
The remaining share of the tax collection corresponds mainly to taxes on the use of particular goods or the performance of activities, e.g., those related to motor vehicles, and customs duties collected for the EU.
There are 17 regions or autonomous communities. Two of them, the Basque Country and Navarre, have special tax regimes. The tax brackets and tax rates above correspond to the 15 remaining regions.
Some of these tax credits, such as that given to working mothers with children below three, are refundable, i.e., they are paid even if personal income tax liabilities are zero.
The dataset is a large administrative sample of 2015 tax returns, which includes almost the complete set of fiscal and socio-demographic information taxpayers provide in their returns. It allows calculating, for each taxpayer, the effective gross (i.e., before tax credits) labor income tax rate, the effective gross capital income tax rate, and tax credits as a fraction of gross income. See García-Miralles et al. (2019) for more details.
We employ this process with two mass points of \(\theta \) for two reasons. First, the productivity distribution in the data has fatter tails than the normal. Second, it is well known that heterogeneous-agents economies have trouble explaining the upper and lower end of the wealth distribution when assuming an AR(1) process with normal innovations.
Our formulation of social security taxes abstracts from the cap on social security contributions. This saves us significant computational time since to calculate the total payments to social security, all we need to know is the total labor income, and not how it is distributed. With a cap, the social security taxes would be \(\max \{{\tau }_{ss}we(\Omega ,j)l_{j},\tau _{ss}I_{cap}\}\). As we indicated above (see footnote 5), the current value of the cap is €4,070 per month or €48,840 per year. In Appendix C, we recalibrate a model economy with such a cap and document the effects of higher progressivity.
The average annual hours worked is taken from the OECD, see https://data.oecd.org/emp/hours-worked.htm.
The EU-KLEMS data can be accessed at http://www.euklems.net/. We use the September 2017 release, revised in July 2018. The methodology of the data is described in O’Mahony and Timmer (2009). The capital stock comprises ten items, including residential structures, transport, communication, computer software, or other machinery equipment. The Spanish National Accounts can be accessed at: https://bit.ly/345fXvG.
The annual population growth rate was 0.086% between 2010-2018 and 0.77% between 2000-2018. Source: The World Bank, https://data.worldbank.org/indicator/SP.POP.GROW?locations=ES&display=graph.
Guner et al. (2019) use data from the EU-SILC from 2006 to 2012. Transfer income includes old-age benefits, survivors’ benefits, sickness benefits, disability benefits, education-related allowances, family/children related allowances and housing allowances, and social exclusion not elsewhere classified.
The corporate income tax collection corresponds to 2015, and it is taken from the OECD Revenue Statistics, https://stats.oecd.org/Index.aspx?DataSetCode=REV. We take the following variables: taxes on income, profits, and capital gains of corporates.
The number is taken from page 125 of “Anexo al Informe Económico Financiero” of the 2018 Social Security budget, available at https://bit.ly/377CoRi.
Estimated as total wages over the number of wage-earners in 2015, obtained from the table Compensation of employees and employment by activity in National Accounts, see https://ine.es/en/daco/daco42/cne15/rem_empleo95_18_en.xlsx.
The concentration of wealth is quite lower in the model than it is in the data. The households at the bottom 20% of the wealth distribution have 3.3% of the total wealth, while the top 20% has 41.7% of it. The corresponding numbers in the data are 1.2% and 65.6%. The data come from the 2014 wave of the Banco de España’s Survey of Household Finances (EFF).
In Appendix C, we document how the tax revenue changes with \(\tau \) in an economy with a cap on social security contributions (see footnote 13). In the economy with a cap, total labor income taxes on high-productivity individuals are lower. As a result, higher values of \(\tau \) generate larger increases in revenue from labor income taxes. The increase in revenue from total taxes, however, is very similar to that resulting from the benchmark economy.
See Appendix D for the derivation of Eq. (10).
In these experiments, income thresholds are determined by the income distribution in the benchmark economy. For example, 1% of individuals earn above €94,974 in the benchmark economy. With higher taxes, the aggregate labor supply and output decline (see the first two rows of each panel of Table 8). As a result, the fraction of individuals who pay the additional tax, i.e., those who are above €94,974, are less than 1% in the new steady state.
These reforms lower the income inequality, but, in contrast to changes in \(\tau \), the effects are small. The Gini index for total income, for example, declines from 0.319 to 0.308 with a 10 percentage point tax increase on the top 10% of earners, and only to 0.316 with a 10 percentage point tax increase on the top 1%.
As we document in Table 5, the benchmark economy generates a lower concentration of taxes paid at the top of the income distribution. This might allow us to obtain a relatively larger increase in tax revenue from higher taxes on the top earners.
See the document “Coalición progresista. Un nuevo acuerdo para España”, available at https://bit.ly/2w78Ypf.
These statistics were computed from the administrative dataset on tax returns referred to on footnote 11. As in García-Miralles et al. (2019), we restrict the sample to taxpayers with positive total gross income, non-negative gross income from different sources (labor, capital and self-employment), and average tax rates below the maximum statutory marginal tax rate.
Monthly earnings correspond to the variable py200g in ECV, whereas hours correspond to the variable pl060.
References
Almunia M, Lopez-Rodriguez D (2019) The elasticity of taxable incomen in Spain: 1999–2014. SERIEs - J Span Econ Assoc 10:281–320
Altonji JG (1986) Intertemporal substitution in labor supply: evidence from micro data. J Polit Econ 94:S176–S215
Badel A, Hugget M, Luo W (forthcoming) Taxing top earners: a human capital perspective. Econ J. https://doi.org/10.1093/ej/ueaa021
Bénabou R (2002) Tax and education policy in a heterogeneous agent economy: what levels of redistribution maximize growth and efficiency? Econometrica 70:481–517
Blanchard O, Rodrik D (2019) We have the tools to reverse the rise in inequality, reflections on the conference on combating inequality: rethinking policies to reduce inequality in advanced economies. Peterson Institute for International Economics, October 17-18, 2019. Available at https://drodrik.scholar.harvard.edu/files/dani-rodrik/files/combating_inequality_introduction.pdf. For details of the conference, https://www.piie.com/events/combating-inequality-rethinking-policies-reduce-inequality-advanced-economies
Bover O, Casado JM, García-Miralles E, Labeaga JM, Ramos R (2017) Microsimulation tools for the evaluation of fiscal policies at Banco de España, Banco de España Occasional Paper N. 1707
Brüggemann B (2019) Higher taxes at the top: the role of entrepreneurs, Working Paper
Caucutt EM, İmrohoroğlu S, Kumar KB (2003) Growth and welfare analysis of tax progressivity in a heterogeneous-agent model. Rev Econ Dyn 6:546–577
Chetty R (2012) Bounds on elasticities with optimization frictions: a synthesis of micro and macro evidence on labor supply. Econometrica 80:969–1018
Conesa JC, Krueger D (2006) On the optimal progressivity of the income tax code. J Monet Econ 53:1425–1450
Conesa JC, Krueger SKD (2009) Taxing capital? Not a bad idea after all!. Am Econ Rev 99:25–48
De Nardi M, Fella G, Yang F (2017) Macro models of wealth inequality. In: Boushey H, DeLong B, Steinbaum M (eds) After piketty: the agenda for economics and inequality. Harvard Univeristy Press, Boston
Diamond P, Saez E (2011) The case for a progressive tax: from basic research to policy recommendations. J Econ Perspect 25:165–190
Diamond PA (1998) Optimal income taxation: an example with a U-shaped pattern of optimal marginal tax rates. Am Econ Rev 88:83–95
Domeij D, Flodén M (2006) The labor-supply elasticity and borrowing constraints: why estimates are biased. Rev Econ Dyn 9:242–262
Erosa A, González B (2019) Taxation and the life cycle of firms. J Monet Econ 105:114–130
Erosa A, Koreshkova T (2007) Progressive taxation in a dynastic model of human capital. J Monet Econ 54:667–685
Farhi E, Werning I (2013) Insurance and taxation over the life cycle. Rev Econ Stud 80:596–635
Fève P, Matheron J, Sahuc J-G (2018) The horizontally S-shaped Laffer curve. J Eur Econ Assoc 16:857–893
García-Miralles E, Guner N, Ramos R (2019) The Spanish personal income tax: facts and parametric estimates. SERIEs 10:439–477
Golosov M, Troshkin M, Tsyvinski A (2016) Redistribution and social insurance. Am Econ Rev 106:359–386
Guner N, Kaya E, Sánchez Marcos V (2019) Labor market frictions and lowest low fertility, Working Paper
Guner N, Lopez-Danieri M, Ventura G (2016) Heterogeneity and government revenues: higher taxes at the top? J Monet Econ 80:69–85
Heathcote J, Storesletten K, Violante GL (2017) Optimal tax progressivity: an analytical framework. Q J Econ 132:1693–1754
Heathcote J, Tsujiyama H (2019) Optimal income taxation: Mirrlees Meets Ramsey, Federal Reserve Bank of Minneapolis Staff Report 507
Holter HA, Krueger D, Stepanchuk S (2019) How do tax progressivity and household heterogeneity affect laffer curves? Quant Econ 10:1317–1356
Hubmer J, Krusell P, Smith AA (2018) A comprehensive quantitative theory of the U.S. Wealth Distribution, Working Paper
Imai S, Keane MP (2004) Intertemporal labor supply and human capital accumulation. Int Econ Rev 45:601–641
İmrohoroğlu A, Kumru ÇS, Nakornthab A (2018) Revisiting tax on top income, ANU Working Papers in Economics and Econometrics # 660
Kaplan G (2012) Inequality and the life cycle. Quant Econ 3:471–525
Kaymak B (2016) The evolution of wealth inequality over half a century: the role of taxes, transfers and technology. J Monet Econ 77:1–25
Keane M, Rogerson R (2015) Reconciling micro and macro labor supply elasticities: a structural perspective. Annu Rev Econ 7:89–117
Kindermann F, Krueger D (2018) High marginal tax rates on the top 1%?. Lessons from a Life Cycle Model with Idiosyncratic Income Risk, Mimeo
Kopczuk W (2019) Reflections on taxation in support of redistributive policies. Prepared for “Combating Inequality: Rethinking Policies to Reduce Inequality in Advanced Economies” (MIT Press, edited by Olivier Blanchard and Dani Rodrik)
López-Rodríguez D, García Ciria C (2018) Spain’s tax structure in the context of the European Union, Banco de España Occasional Paper 1810
Macnamara P, Pidkuyko M, Rossi R (2020) The long-run effects of marginal tax changes across time, Mimeo
MaCurdy TE (1981) An empirical model of labor supply in a life-cycle setting. J Polit Econ 89:1059–1085
Mirrlees JA (1971) An exploration in the theory of optimum income taxation. Rev Econ Stud 38:175–208
Neisser C (2018) The elasticity of taxable income: a meta-regression analysis, IZA DP No. 11958
OECD (2019) Tax policy reforms 2019: OECD and selected partner economies. OECD Publishing, Paris, France. https://doi.org/10.1787/da56c295-en
O’Mahony M, Timmer MP (2009) Output, input and productivity measures at the industry level: The EU KLEMS database. Econ J 119:374–403
Ramsey FP (1927) A contribution to the theory of taxation. Econ J 37:47–61
Saez E (2001) Using elasticities to derive optimal income tax rates. Rev Econ Stud 68:205–229
Saez E, Slemrod J, Giertz S (2012) The elasticity of taxable income with respect to marginal tax rates: a critical review. J Econ Lit 50:3–50
Saez E, Zucman G (2019) The triumph of injustice: how the rich dodge taxes and how to make them pay. W. W. Norton & Company, New York
Serrano-Puente (2020) Optimal progressivity of personal income tax: a general equilibrium evaluation for Spain, Working Paper
Storesletten K (2019) How should taxes respond to rising inequality? Presidential Address, 34th Annual Congress of the European Economic Association
Storesletten K, Telmer CI, Yaron A (2004) Consumption and risk sharing over the life cycle. J Monet Econ 51:609–633
Trabandt M, Uhlig H (2011) The Laffer curve revisited. J Monet Econ 58:305–327
Ventura G (1999) Flat tax reform: a quantitative exploration. J Econ Dyn Control 23:1425–1458
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This is a revised version of the Presidential Address delivered by the first author at the 43rd Symposium of the Spanish Economic Association in Madrid in December 2018. We thank Micole De Vera, Borja Petit, Gustavo Ventura, and seminar participants at the 43rd Symposium and Universidad Autónoma de Madrid, for comments and discussions. The views expressed in this paper are those of the authors and do not necessarily coincide with the views of the Banco de España or the Eurosystem. Guner acknowledges financial support from the Spanish Ministry of Economy and Competitiveness, Grant ECO2014-54401-P. López-Segovia gratefully acknowledges funding from the Fundación Ramón Areces and from Spain’s Ministerio de Economía, Industria y Competitividad (María de Maeztu Programme for Units of Excellence in R&D, MDM-2016-0684). The authors declare that they have no conflict of interest. This article does not contain any information that requires informed consent.
Appendices
Appendices
1.1 Appendix A: Definition of equilibrium
In this appendix, we define a stationary recursive competitive equilibrium. To this end, denote an individual’s state by \(x=(a,\Omega )\), \(x\in \mathbf {X}\), where a are asset holdings and \(\Omega \) are the idiosyncratic productivity shocks. The set \(\mathbf {X}\) is defined as \(\mathbf {X}\equiv [0,\bar{a}]\times \mathbf {\Omega }\), where \(\bar{a}\) stands for an upper bound on asset holdings. Let \(\psi _{j}\), all \(j=1,...,J\), be a probability measure on subsets of the individual state space. Let (\(\mathbf {X}\), \(B(\mathbf {X)}\), \(\psi _{j}\)) be a probability space where \(B(\mathbf {X)}\) is the Borel \(\sigma \)-algebra on \(\mathbf {X}\). In equilibrium, the probability measure \(\psi _{j}\) must be consistent with individual decision rules that determine the asset position of individual agents at a given age, given the asset history and the history of labor productivity shocks. Therefore, it is generated by the law of motion of the productivity shocks \(\Omega \) and the asset decision rule a(x, j). Let permanent shocks \(\theta \) be distributed according to a probability distribution \(\Gamma _{\theta }(\theta ),\) and the persistent shock z be represented by an age-invariant transition function \(\text {Prob}(z_{j+1}=z^{\prime }|z_{j}=z)=\Gamma _{z}(z^{\prime },z).\) These shocks are independently distributed across agents, and the law of large numbers holds.
The distribution of individual states across age-1 agents is determined by the initial exogenous distribution of labor productivity shocks \(\Gamma _{\theta }\) and persistent innovations, since agents are born with zero assets. For agents \(j>1\) periods old, the probability measure is given by the recursion
where
A stationary recursive competitive equilibrium is a collection of decision rules c(x, j), a(x, j), l(x, j), factor prices w and r, taxes paid \(T_{l}(x,j)\) and \(T_{k}(x,j)\), transfers received \(TR_{c}(x,j)\) and \(TR_{m}(x,j),\) per-capita accidental bequests A, social security transfers b, aggregate capital K, aggregate labor L, government consumption G, a payroll tax \(\tau _{ss}\), a proportional capital tax \(\tau _{k},\) a proportional consumption tax \(\tau _{c},\) and (\(\psi _{1},\psi _{2},...,\psi _{N}\)) such that:
-
1.
Given prices and the tax and transfer system, c(x, j), a(x, j) and \(l(x,j)\,\ \)are optimal decision rules determined by Equation (7).
-
2.
Factor prices are determined competitively: \(w=F_{2}(K,L)\) and \(r=F_{1}(K,L)-\delta \)
-
3.
Markets clear:
-
(a)
\(\sum _{j}\mu _{j}\int _{X}(c(x,j)+a(x,j))\mathrm{d}\psi _{j}+G=F(K,L)+(1-\delta )K\)
-
(b)
\(\sum _{j}\mu _{j}\int _{X}a(x,j)\mathrm{d}\psi _{j}=K\)
-
(c)
\(\sum _{j}\mu _{j}\int _{X}l(x,j)e(z,j)\mathrm{d}\psi _{j}=L\)
-
(a)
-
4.
Distributions are consistent with individual behavior:
$$\begin{aligned} \psi _{j+1}(B)=\int _{X}P(x,j,B)\mathrm{d}\psi _{j} \end{aligned}$$for \(j=1,...,N-1\) and for all \(B\in B(\mathbf {X})\).
-
5.
The government budget constraint is satisfied:
$$\begin{aligned} G+\sum _{j}\mu _{j}\int _{X}[T_{c}(x,j)+T_{m}(x,j)]\mathrm{d}\psi _{j}=\sum _{j}\mu _{j}\int _{X}[T_{l}(x,j)+T_{k}(x,j)]\mathrm{d}\psi _{j}+A, \end{aligned}$$where
$$\begin{aligned} A=\left[ \sum _{j}\mu _{j}(1-s_{j+1})\int _{X}(a(x,j)(1+r))\mathrm{d}\psi _{j}\right] \end{aligned}$$ -
6.
Social security benefits equal taxes:
$$\begin{aligned} \tau _{ss}wL=b\sum _{j=J_{R}+1}^{N}\mu _{j}. \end{aligned}$$
Appendix B: Calibration details
1.1 B.1: Age profiles of inequality
We use repeated cross sections of the Encuesta de Condiciones de Vida (ECV) for 2004-2012 to produce the age profile of mean and variance of log hourly wages. The ECV is an annual household survey conducted by the Spanish Statistical Institute, which provides data on income and labor status, among other items. The survey is harmonized at the European Union level, where it is known as the European Union Statistics on Income and Living Conditions (EU-SILC).Footnote 32
We compute hourly wages by dividing the total household gross monthly earnings over four times the total weekly amount of hours worked in the main job.Footnote 33 We deflate hourly wages by the CPI, obtained from the Spanish Statistical Institute.Footnote 34 The sample is restricted to households that have the main earner between age 25 and 64. We further restrict the sample to observations with hourly wages that are above 50% of the minimum wage, and total weekly hours that are at least 5. Moreover, for the computation of household aggregates, we limit the sample to household members with information on both monthly earnings and hours.
The age profile of hourly wages is the vector \(\beta _j\)’s from the following regression:
where \(\text {log }w_{jt}\) is the average log real hourly wage of households aged j in year t, where the age of the household is that of the main earner, \(D_j\) are age-fixed effects, \(D_t\) are year-fixed effects, \(j=\{25,26,...,64\}\), and \(t=\{2004,2005,...,2012\}\). We rescale the vector of \(\beta _j\)’s so that \(\beta _{25}=\frac{1}{T}\sum _{t}{\text {log }w_{25,t}}\), i.e., the first coefficient is rescaled to match the average log real hourly wage at age 25. Panel A of Fig. 6 depicts the mean log hourly wages. The life-cycle pattern features large wage increases at the beginning and a flat profile in the years close to retirement.
The age profile of the variance of log hourly wages is the vector of \(\beta _j\)’s of the following regression:
where \(\text {var}(\text {log }w_{jt})\) is the variance of log real hourly wages of households aged j in year t, and the rest of the terms are as before. The vector of \(\beta _j\)’s is again rescaled so that \(\beta _{25}=\frac{1}{T}\sum _{t}{\text {var}(\text {log }w_{25,t})}\).
1.2 B.2: Calibration of labor productivity shocks
Consider the labor market productivity of an individual i of age j:
where
The cross-sectional variance is given by
where the \(\sum _{k=0}^{j-1}\rho ^{2k}\) terms converges to \(\sigma _{\eta }^{2}/(1-\rho ^{2})\) for \(|\rho |<1.\)
As a result, the parameters \(\{\sigma _{\theta }^{2}, \rho , \sigma _{\eta }^{2}\}\) determine how \(Var(\log e_{ij})\) changes by j. In particular, \(Var(\log e_{i0})=\sigma _{\theta }\), \(\Delta _{j}Var(\log e_{ij})=\sigma _{\eta }^{2}\rho ^{2j}\), and \(\frac{\Delta _{j}^{2}Var(\log e_{ij})}{\Delta _{j}Var(\log e_{ij})}=1+\rho ^{-2}\). We calibrate \(\{\sigma _{\theta }^{2}, \rho ,\sigma _{\eta }^{2}\}\) to minimize the distance between \(Var(\log e_{ij})\) in the data and in an artificial sample of 20,000 individual wages simulated from Equation (A.3). This procedure produces \(\sigma _{\theta }^{2}=0.0897, \rho =0.9831\), and \(\sigma _{\eta }^{2}=0.0052\). Panel B of Fig. 6 shows the model fit. As we compute \({\sigma _{\theta }^{2}, \rho , \sigma _{\eta }^{2}}\) from the EU-SILC without removing the bottom 10% or the top 1% of households, this procedure assumes that the survey data on wages do not capture individuals who are at the top (those with \(\overline{\theta }\)) and the bottom (those with \(\underline{\theta }\)) of labor productivity distribution, while the administrative data on tax returns do. The Gini index for total household labor income in the EU-SILC sample was 0.33. The same statistic in the tax returns data was 0.48. As a result, once we introduce \(\overline{\theta }\) and \(\underline{\theta }\), we target income inequality from the tax returns in Table 4.
Appendix C: Economy with a cap on social security contributions
In the benchmark economy, the total tax payment of an individual is given by
where \(I_{l}=we(\Omega ,j)l_{j}\) and \(I_{k}=ra_{j}\).
An advantage of this formulation is that, to calculate total contributions to the social security system, all we need to know is the total labor income in the economy, and not how it is distributed. In practice, there is cap on social security contributions, i.e., total social security contributions cannot be larger than a certain amount. This cap is calculated as social security taxes on a maximum labor income, which is €4, 070 per month or €48, 840 per year. Then, the social security tax of an individual is given by
where in the second line we report the cap as a multiple of mean labor income in the economy.
The parameter values of the model economy with a cap on social contributions are the same as of the benchmark economy, except for the payroll tax rate, \(\tau _{ss}\), which now takes the value of 0.33, and the top and bottom values of the permanent shock, \(\bar{\theta }\) and \(\underline{\theta }\), which now take the values of 1.995 and \(-2.15\), respectively. Tables 9 and 10 show the model performance. In Table 11, we repeat our main experiment, i.e., we change \(\tau \) and report changes in tax revenue from labor and total income. With a cap on social security contributions, high-productivity individuals face lower effective taxes on labor income. As a result, in this economy there is potentially more room to make taxes more progressive. Indeed, the level of \(\tau \) that maximizes the revenue from labor income taxes is higher. The taxes from labor income are maximized with \(\tau =0.225\). The increase in tax collection from labor income is 1.7%. This increase is about twice as high as the one in the benchmark economy, where the level of \(\tau \) that maximized the revenue from labor income taxes was 0.19.
The level of \(\tau \) that maximizes the total tax collection is again much lower. In the benchmark economy without a cap on social security contributions, \(\tau =0.025\) maximized the total tax collection and the increase in taxes was 2.8% (see Table 6). Now the total tax collection is maximized at \(\tau =0.05\) and the increase in the tax revenue is 2.15%. This is very similar, indeed a little smaller, to what we obtain in an economy without a cap.
Appendix D: Derivation of Equation (10)
The total taxes on labor income are given by
Let us drop the subscript l for the ease of exposition, and let \(I=\frac{I^{*}}{\overline{I}},\) where \(I^{*}\) is labor income in euros. Treating \(\overline{I}\) as a parameter, the total taxes can be written as
The marginal tax rate for income level I is given by
With a x percentage points higher marginal tax rate for income above \(\widehat{I}\), the marginal taxes become
As a result, the total tax function under the new marginal tax schedule is given by
where \(\widehat{I^{*}}\) is the threshold in euros, i.e., \(\widehat{I^{*}}=\widehat{I}\cdot \overline{I}\). Evaluating these integrals gives
Given Equation (A.4), we get
Appendix E: Increase in taxes for high income earners
Reform of the statutory marginal tax rates. Notes: This figure plots the changes in the 2015 statutory marginal tax rates implied by a reform that increases the marginal rates at the very top of the income distribution. Specifically, the labor income marginal tax rate is increased by 2 percentage points for taxpayers earning more than €130,000 of labor income and 4 percentage points for taxpayers earning more than €300,000. Also, the capital income marginal tax rate is raised by 4 percentage points for taxpayers earning more than €140,000 of capital income
Appendix F: Economy with a higher Frisch elasticity
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guner, N., López-Segovia, J. & Ramos, R. Reforming the individual income tax in Spain. SERIEs 11, 369–406 (2020). https://doi.org/10.1007/s13209-020-00224-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-020-00224-2