From bilateral two-way to unilateral one-way flow link-formation

Abstract

We provide a model that allows for a transition between the simplest variation of two basic models of strategic network formation: Bala and Goyal’s one-way flow model without decay, where links can be unilaterally formed, and a version without decay of Jackson and Wolinsky’s connections model based on bilateral formation of links. In the transitional model introduced here, these two benchmark models appear as extreme cases. We study efficiency and Nash, strict Nash and pairwise Nash stability for the intermediate model. Dynamics are also discussed.

1 Introduction

Economic literature is paying increasing attention to the impact of network structures on economic and social situations. A network consists of nodes and edges. With different degrees of crispness and to a more or less conspicuous extent, such structures underlie a huge variety of situations in different fields.¹ Abstracting away the nature of its nodes and its edges (individuals and friendships, towns and connecting roads/trains/flights; species and trophic interactions; firms, banks or countries and commercial or financial relations,...), the mathematical skeleton of a network is a graph, an object that is both simple (it is described by a matrix) and extremely complex (that matrix may be huge). This has led to the development of tools for interpreting the complex network structures that arise in different contexts. A different line of theoretical research addresses the question of how networks form, perform and stabilize. This line of research is attracting considerable attention with significant contributions in the economic literature, among them the two basic models of strategic network formation. In Jackson and Wolinsky’s (1996) connections model, pairs of individuals may agree to form links, thus forming a network through which information (or some other good) flows. The benefit that such a network brings to an individual is the value of the information or other goods received through it, minus the cost of the links that he/she pays for. In contrast with this bilateral model of link-formation, Bala and Goyal (2000a) introduce a model where links can be formed unilaterally by any player, with two variants: the one-way flow model, where the flow through a link runs towards a player only if he/she supports it, and the two-way flow model, where the flow runs in both directions irrespective of which player supports the link. In these three models the creation of a link entails positive externalities as it contributes to easing the flow through the network.

In the simplest variants of the seminal models, efficient networks are easily characterized and conditions for their stability established. Efficient/stable structures prove to be simple and entirely different in each model (e.g., wheels, trees, stars). This is at once interesting (“emblematic” structures arise from simple models of network formation) and insufficient (in the real world, much more complex network structures occur). It should be emphasized that none of these basic models was tailored to fit any particular or specific situation of an economic or other nature. Nevertheless, they have been and continue to be instrumental in many applied works. Also, as a result of this combination of appeal and insufficiency, these models have been extended in different directions² always taking each one as a starting point. In contrast with these extensions, the originality of this research project lies in addressing the provision and study of “transitional” models which in some sense “bridge the gap” between the basic models. The motivation is manifold. These basic models represent “extreme” cases in a sense. Depending on the model, the formation of a link is either the result of collaboration between two agents or that of an individual decision. This does not cover situations where both options are feasible. In general terms, if links represent channels of transmission of any sort, it makes sense to consider situations where both options are feasible. It seems natural then to assume that the transmission through links that result from collaboration is better than through those created unilaterally. The quality of an imperfect transmission can be interpreted in two ways: as the effect of friction or “decay”, when only a fraction of the information at one node reaches the other, or as the level of “reliability”, i.e., the probability that the information at one node reaches the other.³

In other words, is it possible to unify at least partially the seminal models? If so, which structures are efficient and/or stable in such intermediate models? What is the impact of assuming both unilateral and bilateral formation of links to be feasible? Are the basic models robust w.r.t. these modifications? Is it possible to augment the repertoire of admissible actions and still keep the model tractable?⁴ This paper is a small contribution in this line of research in the wake of these benchmark models. In two previous papers we have studied two transitional models. Olaizola and Valenciano (2014) introduces a model that integrates Bala and Goyal’s one-way and two-way flow models without decay as particular extreme cases of a more general one. Olaizola and Valenciano (2015a) provides a new hybrid model which has a variant of Jackson and Wolinsky’s connections model without decay and Bala and Goyal’s two-way flow model as extreme cases. The point of this paper is to complete the “triangle”, i.e. to provide and study a transitional model between the remaining pair: the variant of Jackson and Wolinsky’s model without decay and Bala and Goyal’s one-way flow model as extreme cases. To achieve this we assume that a link resulting from collaboration of two agents provides a better channel of transmission than a link sponsored by only one agent. As this “side” of the triangle has a common “vertex” with that studied in Olaizola and Valenciano (2015a), i.e. Jackson and Wolinsky’s model without decay, this transition provides a point of comparison with the results for efficiency, stability, and dynamics in that transitional model. In particular, this evidences the different impact on efficiency and stability of assuming the feasibility of different types of unilateral link—undirected and directed—giving rise to different externalities. To shorten the paper by avoiding redundancies whenever the results essentially coincide we omit the proofs and emphasize the differences.

The rest of the paper is organized as follows. Section 2 reviews Jackson and Wolinsky’s (1996) connections model of network formation and Bala and Goyal’s (2000a) one-way and two-way flow models. Section 3 briefly presents the models that bridge the gap between any two of these. The rest of the paper concentrates on the model bridging Jackson and Wolinsky’s (1996) connections model and Bala and Goyal’s (2000a) one-way flow model. The questions of efficiency and stability in this model are addressed in Sects. 4 and 5 respectively. Section 6 is devoted to dynamics. Finally, Sect. 7 summarizes the main conclusions and indicates some lines of further research.

2 Three strategic models of network formation

Following Jackson and Wolinsky (1996) and Bala and Goyal (2000a), in fact rephrasing them in order to bridge the gap between different link-formation models, consider a scenario where individuals may invest in links with other individuals, thus creating a network. Namely, let N be the set of agents or players ⁵ who may form links with one another. A map $g_{i}:N\backslash \{i\}\rightarrow \{0,1\}$ specifies the links invested in by player i and is referred to as a strategy of player i. We write $g_{ij}:=g_{i}(j),$ and $g_{ij}=1$ ($g_{ij}=0$) means that i invests (does not invest) to form a link with j. $G_{i}:=\{0,1\}^{N\backslash \{i\}}$ denotes the set of i’s strategies and $G_{N}=G_{1}\times G_{2}\times \cdots \times G_{n}$ the set of strategy profiles. Each strategy profile $g\in G_{N}$ determines a directed graph ⁶ of invested links. When $g_{ij}=g_{ji}=1$, i.e. both players invest in a link, we say that i and j support, or are connected by, a strong link; when only one, say i, invests in it we say that i and j are connected by a weak link supported by i .

Let g be a strategy profile representing players’ link-investments, then $g^{*}$ denotes the associated graph representing the actual network that results from g. Different assumptions lead to different specifications of $g^{*}$, but generally the following assumptions are made: (1) investing in a link entails a cost $c>0$ ⁷; (2) the player at each node has a particular type of information or other good⁸ of value 1 to any other player who receives it intact⁹; (3) if g is the strategy profile and $g^{*}$ is the resulting network, the payoff of a player is given by a

$$\begin{aligned} \Pi _{i}(g)=I_{i}(g^{*})-c_{i}(g), \end{aligned}$$

(1)

where $I_{i}(g^{*})$ is the information received by i through the actual network $g^{*}$, and $c_{i}(g)=c\mu _{i}^{d}(g)$ the cost incurred by i, where $\mu _{i}^{d}(g)$ is the number of links i invests in. Different models specify $g^{*}$ and $I_{i}$ differently, but in all cases a game in strategic form is specified: $(G_{N},\{\Pi _{i}\}_{i\in N})$, where the Nash equilibrium ¹⁰ stability notion can be applied to strategy profiles.

The three basic models relating $g^{*}$ to g alluded to above are as follows:

$$\begin{aligned}&(i)\ \ g_{ij}^{*}\;{:=}\;g_{ij}^{\min }=\min \{g_{ij},g_{ji}\}. \end{aligned}$$

(2)

$$\begin{aligned}&(ii)\ \ g_{ij}^{*}\;{:=}\;g_{ij}. \end{aligned}$$

(3)

$$\begin{aligned}&(iii)\ \ g_{ij}^{*}\;{:=}\;g_{ij}^{\max }=\max \{g_{ij},g_{ji}\}. \end{aligned}$$

(4)

Under assumption (2) only strong links, i.e. those supported by both players, actually form. This is Jackson and Wolinsky’s bilateral link-formation model, where for a link to be established both players must invest in it. Under assumption (3) a directed link forms between two players as soon as one of them invests in it. Thus, in this case a player can create directed links unilaterally. This is Bala and Goyal’s one-way flow model. Finally, under (4) undirected links can be unilaterally created by players. This is Bala and Goyal’s two-way flow model. Note that in the three models strong links may form.

If every node receives intact the value of the players with whom it is connected in $g^{*}$, then, according to each of these specifications of the resulting actual network, i.e. whether $g^{*}$ is given by (2) or (3) or (4), the payoff of a player given by (1) becomes respectively:

$$\begin{aligned} \Pi _{i}^{\text {JW}}(g)= & {} \mu _{i}(g^{\min })-\mu _{i}^{d}(g)c, \end{aligned}$$

(5)

$$\begin{aligned} \Pi _{i}^{\text {BG1}}(g)= & {} \overrightarrow{\mu }_{i}(g)-\mu _{i}^{d}(g)c. \end{aligned}$$

(6)

$$\begin{aligned} \Pi _{i}^{\text {BG2}}(g)= & {} \mu _{i}(g^{\max })-\mu _{i}^{d}(g)c \end{aligned}$$

(7)

where $\mu _{i}(g^{\min })$ ($\mu _{i}(g^{\max })$) is the number of nodes connected to i by a path¹¹ in $g^{\min }$($g^{\max }$), and $\overrightarrow{\mu }_{i}(g)$ is the number of nodes connected to i by an i-oriented path in g. The model specified by (2) and (5) is a variation without decay,¹² of Jackson and Wolinsky’s connections model, i.e. assuming that the flow through a link of the actual network is perfect or without loss. Similarly, (3) and (6) specify Bala and Goyal’s one-way flow model without decay, while (4) and (7) specify Bala and Goyal’s two-way flow model without decay. Observe that in all three models the strategy profile g determines $g^{*}$ and the payoff of every player.

As a reference term, in each of these basic models we have the following results relative to efficient (i.e. maximizing the aggregate payoff) and stable structures where we make use of the following notions. $K\subset N$ is a weak component/a component/a strong component of g if for any two nodes $i,j\in K$, there is a path/an i-oriented path/a path of strong links from j to i in g, and no subset of N strictly containing K meets this condition. A strong component is isolated if none of its nodes is involved in a weak link with a link in another component. A network g is connected/weakly-connected/strongly-connected if N is the unique connected/weakly-connected/strongly-connected component.¹³ A component is minimal if the elimination of any link would increase the number of components in that sense. The size of a component is the number of nodes from which it is formed, and if it consists of a single node, it is a trivial component. A minimally strongly-connected graph is a tree of strong links where any node in the tree can be seen as the root, i.e. a reference node from which there is only one path connecting it with any other.

Proposition 1

In Jackson and Wolinsky’s connections model without decay, with payoffs given by (5):

• (i) The only efficient profiles are the empty profile and the minimally strongly-connected profiles.

• (ii) The nonempty Nash and strict Nash profiles are those where all links are strong and all strong components are minimal.

• (iii) The nonempty pairwise stable¹⁴ profiles are those minimally strongly-connected.

The proof can be seen, for instance, in Olaizola and Valenciano (2015a). As for Bala and Goyal’s well-known results we have:

Proposition 2

(Bala and Goyal 2000a) In Bala and Goyal’s one-way flow model, with payoffs given by (6):

• (i) The only efficient profiles are the empty profile and the oriented wheel.¹⁵

• (ii) The nonempty Nash profiles are those minimally connected.

• (iii) The strict Nash profiles are oriented wheels.

In both models the turning point where the empty network becomes efficient occurs when the other efficient structure also yields 0 aggregate payoff, which depends on c and the number of players.

3 Transitional models

Thus, in terms of weak (singly-supported) vs. strong (doubly-supported) links, in Jackson and Wolinsky’s (1996) connections model only strong links make sense as they are the only ones that actually form, whereas in Bala and Goyal’s (2000a) one-way and two-way flow models only weak links appear in efficient and stable strategy profiles. A transition between Jackson and Wolinsky’s (1996) model without decay and Bala and Goyal’s (2000a) two-way flow model is possible by assuming that information flows through strong links without friction in both directions, and through weak links also in both directions but with some decay. If $\alpha$ ($0\le \alpha \le 1$) is the fraction of a unit of information at a node that flows through a weak link, $\alpha =0$ means no flow and maximal decay, while $\alpha =1$ means perfect flow and no decay. This is the model introduced in Olaizola and Valenciano (2015a). Formally, in that model the actual level of information flow from node j to node i through a link between them when the players’ strategy profile is g, denoted by $g^{\text {JWBG2}}$ is given by

$$\begin{aligned} g_{ij}^{\text {JWBG2}}:=\alpha g_{ij}^{\max }+(1-\alpha )g_{ij}^{\min }, \end{aligned}$$

(8)

with $0\le \alpha \le 1$. Thus the weighted graph $g^{\text {JWBG2}}$ specifies the flow level through each link for a profile in this model.

A similar transition between Jackson and Wolinsky’s (1996) model and Bala and Goyal’s (2000a) one-way flow model is achieved by assuming that information runs through a weak link only towards the node that supports it and with some decay $\alpha$. This is formally captured by replacing $g_{ij}^{\max }$ by $g_{ij}$ in (8), that is, by

$$\begin{aligned} g_{ij}^{\text {JWBG1}}:=\alpha g_{ij}+(1-\alpha )g_{ij}^{\min }, \end{aligned}$$

(9)

with $0\le \alpha \le 1$, so that the weighted graph $g^{\text {JWBG1}}$ specifies the flow level through each link for a profile in this model.¹⁶

This motivates the notion of discounting length of a path from j to i in g, which is the number of weak links in it. Then, the discounting distance from j to i in g, denoted by $\lambda (i,j;g)$, is defined as the discounting length of the path from j to i with the shortest discounting length. Then the payoff of a player in a profile g in this model is

$$\begin{aligned} \Pi _{i}^{\text {JWBG2}}(g)=\sum _{j\in N(i;g)}\alpha ^{\lambda (i,j;g)}-c\mu _{i}^{d}(g), \end{aligned}$$

(10)

with $0\le \alpha \le 1$, where N(i; g) denotes the set of nodes connected to i by a path.

Similarly, (9) motivates the notion of discounting oriented length of a path from j to i in g , which is $\infty$ if the path is not i-oriented and otherwise is the number of oriented weak links in it. The discounting oriented distance from j to i in g, denoted by $\vec {\lambda }(i,j;g)$, is defined as the discounting oriented length of the path from j to i with the shortest discounting oriented length. Note that this distance is not symmetric. Then, the payoff of a player for a profile g in this model is given by

$$\begin{aligned} \Pi _{i}^{\text {JWBG1}}(g)=\sum _{j\in N(i;g)}\alpha ^{\vec {\lambda } (i,j;g)}-c\mu _{i}^{d}(g), \end{aligned}$$

(11)

with $0\le \alpha \le 1$. In the sequel we refer to the model specified by (8) and (10) as “JWBG2 model”, and by “JWBG1 model ” to the one specified by (9) and (11).

Figure 1 shows the “triangle” whose vertices are the benchmark models and its sides the transitional models, and where the model specified in Footnote 16 is referred to as “BG12 model”.

Fig. 1

Transitional models

Example 1

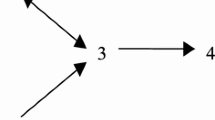
Consider the strategy profile g given by the 5-node graph below, where a strong link is represented by a thick segment, while a weak link is represented by a thin segment only touching the node that supports it.

In JWBG2: player 1 receives a fraction $\alpha$ of the unit of information from players 2 and 3, a fraction $\alpha ^{2}$ of the unit of information at 4, $\alpha ^{3}$ from 5, and pays c for one link. Thus player 1’s payoff is $\Pi _{1}^{\text {JWBG2}}(g)=$ $2\alpha +\alpha ^{2}+\alpha ^{3}-c$. Similarly, $\Pi _{2}^{\text {JWBG2}}(g)=\Pi _{3}^{\text {JWBG2}}(g)=1+2\alpha +\alpha ^{2}-c$, $\Pi _{4}^{\text {JWBG2}}(g)=3\alpha +\alpha ^{2}-2c$, $\Pi _{5}^{\text {JWBG2}}(g)=\alpha +2\alpha ^{2}+\alpha ^{3}$.

In JWBG1 the same profile yields different payoffs, namely: player 1 receives information only from players 2 and 3, a fraction $\alpha$ of the unit of information at each of these nodes, and pays for one link. Thus player 1’s payoff is $\Pi _{1}^{\text {JWBG1}}(g)=$ $2\alpha -c$. Similarly, $\Pi _{2}^{\text {JWBG1}}(g)=$ $\Pi _{3}^{ \text {JWBG1}}(g)=1-c,$ $\Pi _{4}^{\text {JWBG1}}(g)=$ $3\alpha -2c$, $\Pi _{5}^{\text {JWBG1}}(g)=0$.

Remark

• (i) In both JWBG2 and JWBG1 models, the decay matrix or weighted graph (as given by (8) and (9)) encapsulates all the relevant information about the flow through the network.

• (ii) In both models, $\alpha =0$ yields $g^{\text {JWBG1}}=g^{\text {JWBG2}}=g^{\min }$, i.e. Jackson and Wolinsky’s network formation model without decay; while for $\alpha =1$: $g^{\text {JWBG2}}=g^{\max }$ (i.e. Bala and Goyal’s two-way flow model) and $g^{\text {JWBG1}}=g$ (i.e. Bala and Goyal’s one-way flow model).

• (iii) Thus JWBG2 and JWBG1 represent two different transitional models, both starting from Jackson and Wolinsky’s model without decay, but moving away in different directions: each of them towards one of the two variants of Bala and Goyal’s model.

• (iv) In both transitional models, when a link is supported by both players $g_{ij}^{\text {JWBGk}}=g_{ji}^{\text {JWBGk}}(g)=1$ ($k=1,2$), for all $\alpha$. That is, information flows through strong links without friction in both directions.

• (v) In JWBG2 when only one player supports a link, say i, we have $g_{ij}^{\text {JWBG2}}=g_{ji}^{\text {JWBG2}}=\alpha$, i.e. flow through weak links occurs with decay in both directions.

• (vi) In JWBG1 when only one player supports a link, say i , $g_{ij}^{\text {JWBG1}}=\alpha$ and $g_{ji}^{\text {{JWBG1}}}=0$, i.e. flow through a weak link occurs with decay towards the only player supporting it and there is no flow in the opposite direction

• (vii) A comparison between these two transitional models leads to some general remarks which are employed later: both models incorporate all possibilities of Jackson and Wolinsky’s model without decay: strong links with 0-friction, but their stability differs in each of the models. Strong links are less stable w.r.t. withdrawal of support in JWBG2, where a weak link remains after withdrawal of support by one player allowing information to flow in both directions, while in JWBG1 no information flows through the remaining weak link toward the player that withdraws support. As to the stability of weak links, the situation is the opposite (w.r.t. being doubled): weak links are more stable in JWBG2, where the incentives for doubling them are smaller than in JWBG1. Concerning externalities, the externalities of weak links are greater in JWBG2 than in JWBG1.

We now focus on the JWBG1 model, but taking advantage of the results established for JWBG2 in Olaizola and Valenciano (2015a, c). We first address the question of efficiency and then that of stability with particular attention to the stability of efficient networks.

4 Efficiency

The aggregate payoff of a network g is referred to as the value of the network and denoted by v(g). A network g is said to dominate another $g^{\prime }$ if $v(g)\ge v(g^{\prime })$. A network is efficient if it dominates any other for a particular configuration of values of the parameters. In the current setting we should refer to the efficiency of strategy profiles rather than the efficiency of networks, given that different profiles may yield the same actual network. Nevertheless, we refer to efficient (actual) networks, meaning efficiently sustainable by efficient profiles.

We then have the following characterization of efficient networks in the JWBG2.

Proposition 3

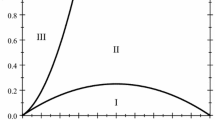
(Olaizola and Valenciano 2015c) In the JWBG2 model with $0\le \alpha <1$, the unique efficient networks are:

• (i) The minimally strongly-connected ones if

  $$\begin{aligned} c<\min \{n/2,n-2\alpha -(n-2)\alpha ^{2}\}.\quad (\text {Region I in Figure }2) \end{aligned}$$

• (ii) The all-encompassing stars of weak links if

  $$\begin{aligned} n-2\alpha -(n-2)\alpha ^{2}<c<2\alpha +(n-2)\alpha ^{2}.\quad (\text {Region II in Figure }2) \end{aligned}$$

• (iii) The empty network if

  $$\begin{aligned} c>\max \{n/2,2\alpha +(n-2)\alpha ^{2}\}.\quad (\text {Region III in Figure } 2) \end{aligned}$$

Fig. 2

Efficiency in JWBG2 $(n=20)$

The following lemma allows to draw some conclusions on efficiency in the JWBG1 model as a corollary.

Lemma 1

If g is an efficient network in the JWBG2 model that does not contain weak links then it is also efficient in the JWBG1 model.

Proof

Denote by $v^{\text {JWBG1}}(g):=\sum \nolimits _{i\in N}\Pi _{i}^{\text {JWBG1}}(g)$ and $v^{\text {JWBG2}}(g)=\sum \nolimits _{i\in N}\Pi _{i}^{\text {JWBG2}}(g)$. Let g be an efficient profile in JWBG2 without weak links. For any profile $g^{\prime }$ we have

$$\begin{aligned} v^{\text {JWBG1}}(g)\overset{(a)}{=}v^{\text {JWBG2}}(g) \overset{(b)}{\ge }v^{\text {JWBG2}}(g^{\prime })\overset{(c)}{\ge } v^{\text {JWBG1}}(g^{\prime }), \end{aligned}$$

where (a) holds whenever g has no weak links, (b) because g is efficient in JWBG2, and (c) holds for any profile because in both models strong links work and cost the same, while weak links in JWBG2 generate greater positive externalities than in JWBG1 at the same cost. Thus, g is efficient also in JWBG1. $\square$

Then we have an immediate corollary from Proposition 3:

Corollary 1

In the JWBG1 model with $0\le \alpha <1$, the empty network and those minimally strongly-connected are also efficient within the regions where they are efficient in the JWBG2 model.

Remark

Note that, unlike Proposition 3, this corollary is not a characterization. It just stems from Proposition 3 and the fact that a network without weak links which is efficient in JWBG2 must be so in JWBG1, where networks containing weak links yield smaller aggregate value than in JWBG2 because of their smaller value ($\alpha -c$ vs. $2\alpha -c$), and smaller externalities (they transmit in only one direction). Corollary 1 states that these structures continue to be efficient in regions I and III in Fig. 2, but it is possible that they are efficient in JWBG1 in wider regions.

Thus there only remains the question of efficient profiles in Region II in Fig. 2. Note that this region contains the segment where $0\le c\le n$ and $\alpha =1$, which corresponds to Bala and Goyal’s two-way flow model without decay in JWBG2 (where efficient networks are those minimally weakly-connected), while in JWBG1 corresponds to Bala and Goyal’s one-way flow model without decay, where oriented wheels are the only efficient structures. Thus one can expect efficient networks containing cycles ¹⁷ in Region II. In fact, as we presently show, oriented wheels can yield a greater aggregate value than minimally strongly-connected networks in this region. This occurs for an n-node oriented wheel if:

$$\begin{aligned} n\left( \alpha +\alpha ^{2}+\cdots +\alpha ^{n-1}\right) -nc>(n-1)(n-2c), \end{aligned}$$

which holds above the curve

$$\begin{aligned} c=\frac{n}{n-2}\left( n-1-\left( \alpha +\alpha ^{2}+\cdots +\alpha ^{n-1}\right) \right) , \end{aligned}$$

(12)

which is a concave function decreasing on $\alpha$, whose value is $n(n-1)/(n-2)$ for $\alpha =0,$ and 0 for $\alpha =1.$ It can be easily seen that for $\alpha \in (0,1)$ this curve cuts across Region II above $c=n-1-2\alpha -(n-2)\alpha ^{2},$ which according to Corollary 1 is the lower boundary of Region II. In other words: above (12) oriented wheels yield a greater aggregate payoff than minimally strongly-connected networks, and below this line and beyond Region I, where they are proven to be efficient, minimally strongly-connected networks still beat the wheel.

We have not been able to characterize efficient networks within Region II. Nevertheless, the following counterexample contradicts the conjecture according to which oriented wheels would be the only nonempty efficient structures in Region II.

Example 2

Let $g_{1}$ be a 5-node oriented wheel and $g_{2}$ a 5-node network consisting of two 3-node oriented triangles sharing a node. Then, it is easy to check that $v(g_{2})-v(g_{1})=\alpha +3\alpha ^{2}-\alpha ^{3}-3\alpha ^{4}-c$. Then, wheel $g_{1}$ is beaten by 2-cycle network $g_{2}$ whenever $c<\alpha +3\alpha ^{2}-\alpha ^{3}-3\alpha ^{4}$, which leaves room for c for all $\alpha \in (0,1)$ given that the right-hand term is positive for all $\alpha \in (0,1)$.

5 Stability

As in the JWBG2 model, in the JWBG1 model both a strictly non-cooperative approach and one admitting (or requiring) bilateral agreements to form new strong links make sense. We therefore examine the question of stability from two points of view: one purely non-cooperative, focusing on Nash and strict Nash equilibrium, and the other allowing for pairwise formation of links. Note that in the transitional models the set of options available to any player is richer than in Jackson and Wolinsky’s setting, where the only unilateral move is severing a link. A player can now create a new weak link or make an existing weak one strong. Although a weaker version is possible, we use a strong version of the pairwise stability notion referred to in the literature as pairwise Nash stability, which in fact refines both the Nash equilibrium and pairwise stability.¹⁸ A strategy profile g is pairwise Nash stable if it is a Nash equilibrium and no pair of players has incentives to form a new strong link. When the results and their proofs are very similar to those in Olaizola and Valenciano (2015a), we omit the proofs, emphasize the differences and concentrate on the intuition behind them.

5.1 Stability for $c<1$

The following lemma utilizes some remarks made in Sect. 3 comparing JWBG2 and JWBG1 models to transfer stability results for JWBG2 established in Olaizola and Valenciano (2015a) to JWBG1.

Lemma 2

Let g be a strategy profile without weak links. Then: (i) If g is a Nash (strict Nash) profile in the JWBG2 model, then g is also a Nash (strict Nash) profile in the JWBG1 model; (ii) If g is a pairwise Nash profile in the JWBG2 model, then g is also a pairwise Nash profile in the JWBG1 model.

Proof

Assume that g, without weak links, is a Nash profile in JWBG2. If g is empty, then no player has incentives to create a weak link nor do any pair of players have incentives to form a strong one, but then the same must be true in JWBG1.

If g consists of strong links only, no cycles are possible and no player involved in a strong link has incentives to break it, but then the same must be true in JWBG1, since a weak link remains after withdrawal of support by one player in JWBG2, while in JWBG1 no information flows through the remaining weak link toward the player that withdraws support. As for forming new weak or strong links, if there are no incentives to form any in JWBG2 the same must be true in JWBG1, given that an improvement achieved by a weak link in JWBG2 can be mimicked by a weak link in JWBG1, and new strong ones are equally feasible in both if pairwise coordination is assumed. The same holds for strict Nash profiles and pairwise Nash profiles only containing strong links. $\square$

The following proposition characterizes stable architectures within the region below the line $c=1-\alpha .$

Proposition 4

In the JWBG1 model, with $0<\alpha <1$ and $0<c<1-\alpha :$

• (i) If $c\ge \alpha ,$ a profile is Nash (strict Nash) stable if and only if it is minimally strongly-connected or otherwise if all links are strong, all strong components are minimal, and the maximal size of a strong component is less than or equal to (strictly less than) $c/\alpha$.

• (ii) If $c<\alpha ,$ a profile is Nash stable if and only if it is minimally strongly-connected; moreover such a profile is also strict Nash stable.

• (iii) For the whole range of values, a profile is pairwise Nash stable if and only if it is minimally strongly-connected.

The proof of an identical result for JWBG2 [Proposition 3 in Olaizola and Valenciano (2015a)] can be replicated in JWBG1 and is omitted. But note that, apart from the uniqueness (i.e. the “only if” part), the stability follows from that result and Lemma 2.

Thus Proposition 4 characterizes the Nash, strict Nash and pairwise Nash stable architectures within the region $c<1-\alpha .$ Indeed, unlike in JWBG2, the same structures remain stable above the line $c=1-\alpha$ as far as $c<1$, but they are not the only ones which are stable above this line as we shall show presently. The following lemma allows a partial characterization above that line and below $c=1$.

Lemma 3

In the JWBG1 model with $0<\alpha <1$ and $1-\alpha \le c<1,$ in a Nash profile any link which is not part of a cycle is necessarily strong. In particular, peripheral¹⁹ players are connected by strong links.

Proof

Let g be a Nash profile and let i and j be two players connected by a weak link which is not part of any cycle. Assume i is the only node supporting it, then j receives no information from i, while if j makes the link strong at a cost $c<1$, j improves its payoff in at least $1-c>0$ , which contradicts g being a Nash profile. $\square$

Comment

Note that this is false in JWBG2, where no cycle is possible in a Nash profile, and where above the line $c=1-\alpha$ a strong link connecting a peripheral node is unstable (the non peripheral player supporting it would have incentives for withdrawing its support). This is an important difference between these two models, which makes tree core-periphery profiles²⁰ unstable above $c=1-\alpha$ in JWBG1. Unlike in JWBG2 we have:

Proposition 5

In the JWBG1 model, with $0<\alpha <1$ and $1-\alpha \le c<1,$ then (i) , (ii) and (iii) in Proposition 4 remain true if it is assumed that the profile contains no cycles.

Proof

Assume g is a Nash profile with no cycles. By Lemma 3, within this range of values of $\alpha$ and c all links are strong, and no superfluous link would be supported. Therefore all strong components are minimal. Then the proof of (i), (ii) and (iii) follows the same steps as in Proposition 3 in Olaizola and Valenciano (2015a). $\square$

Fig. 3

Stability $(c<1)$

Remark

• (i) Figure 3 illustrates the situation described by Propositions 4 and 5. The left-hand side of the rectangle, i.e. $\alpha =0$, represents a version of Jackson and Wolinsky’s connections model without decay, where Nash and strict Nash profiles are those where all links are strong and all strong components are minimal, and pairwise Nash stable profiles are those which are minimally strongly-connected. In region S, above $c=s\alpha$, all minimally strongly-connected profiles as well as those described in Proposition 4-(i), where the size of the greatest strong component is less than or equal to (strictly less than) s, are Nash (strict Nash) stable. Moreover, below the straight line $c=1-\alpha$ these are the only Nash (strict Nash) structures, while above that line they are the only Nash (strict Nash) structures without cycles. As one moves right, i.e. as $\alpha$ increases, from the side $\alpha =0$, all the structures characterized in Proposition 1-(ii) as Nash and strict Nash when $\alpha =0$ remain strict Nash as long as the largest strong component (if the profile is not strongly-connected) is not large enough to make if profitable for any player in another component to form a weak link with any player in it (i.e. if it is smaller than $c/\alpha$). When $c/\alpha >1$ but this value is very close to 1, apart from minimally strongly-connected profiles only the empty network -where all strong components are singletons- remains strict Nash among such profiles. Beyond that point, i.e., when $c<\alpha$ and $c<1-\alpha$, the only Nash and strict Nash stable profiles are those minimally strongly-connected. The same is true when $c\ge 1-\alpha$ if we confine our attention to profiles with no cycles.

• (ii) Only minimally strongly-connected profiles are pairwise Nash stable below the line $c=1-\alpha ,$ and the same is true above that line for strategy profiles without cycles. But in view of Proposition 4-( ii) and Proposition 5, below the line $c=\alpha$ pairwise Nash stability adds nothing to (i.e. does not refine) Nash stability, given that in this case bilateral coordination is irrelevant because it does not really offer new chances to the players.

• (iii) A comparison with the results in Olaizola and Valenciano (2015a) for the same region is pertinent here. Below the line $c=1-\alpha$ the results are the same as in Olaizola and Valenciano (2015a). However, above $c=1-\alpha$ the results diverge. In the current model the same structures remain stable as far as $c<1$, which is not the case in Olaizola and Valenciano (2015a) above $c=1-\alpha$. Indeed new different structures appear in each model, as becomes clear when Proposition 5 is compared with the results in Olaizola and Valenciano (2015a). This difference is enhanced by the discussion in Sect. 5.3.

5.2 Stability for $c>1$

The following simple lemma has strong consequences.

Lemma 4

In the JWBG1 model with $0<\alpha <1$ and $c>1$, in a Nash profile peripheral players are connected by weak links supported by them.

Proof

Let g be a Nash profile. Assume i is peripheral in g and j is the only node with which i is involved in a link. As $c>1$, if j supported this link i’s reward for it would be $1-c$ or $\alpha -c$, depending on whether $g_{ij}=1$ or $g_{ij}=0$, but in both cases less than 0. Thus the only link in which i is involved must be weak and supported by i. $\square$

In view of this, above the line $c=1$, in equilibrium peripheral players must be harmlessly parasitical: they receive enough for them to be worth paying for the connection, but they contribute nothing to others’ welfare. Note also that all the structures whose stability below the line $c=1$ has been established in Propositions 4 and 5 are not stable above this line, because the nodes supporting strong links with peripheral nodes of a tree would withdraw support for them as soon as $c>1$. But, as shown in 5.1, other structures may be stable above the line $c=1-\alpha$, for instance, oriented wheels. Moreover, as a consequence of Lemma 4 we have the following corollary:

Corollary 2

In the JWBG1 model, with $0<\alpha <1$ and $c>1$, a nonempty Nash profile necessarily contains cycles.

Proof

Assume g is a nonempty Nash network. If g contains no cycles it must be formed by one or more trees. Without loss of generality, assume g is a tree. By Lemma 4, its peripheral nodes must be connected by weak links supported by them. Let P(g) be the set of peripheral players in g, and consider the subgraph that results from eliminating them. Given that peripheral players in that subgraph receive nothing from those peripheral ones in g, they must also support their weak links. By reiterating this reasoning, after a finite number of steps a stage must be reached where one is left with either one or two nodes. In the first case, those that support links with the single remaining node receive $\alpha <1$ and pay $c>1$ for it, which contradicts the notion that g is a Nash network. In the second case, neither player has an incentive to form either a weak or a strong link, which is a contradiction. $\square$

Thus, above $c=1$ stability entails the existence of cycles.

5.3 Stability with cycles

By Lemma 3, above the line $c=1-\alpha$, when $c<1$ in equilibrium all links are strong unless there are cycles. Nevertheless, when $c\ge 1-\alpha$ weak links may actually occur in equilibrium if there are cycles. The following discussion shows that the stability of oriented wheels (i.e. the only strict Nash architecture for Bala and Goyal’s one-way flow model without decay) when $c<1$ is confined to a region close to $\alpha =1$, i.e. to Bala and Goyal’s one-way flow model. Consider the n-player profile consisting of n weak links which form an oriented wheel. No node has an incentive to sever the one link that it is supporting out of the two in which it is involved and to double the other one if

$$\begin{aligned} \alpha +\alpha ^{2}+\alpha ^{3}+\cdots +\alpha ^{n-2}+\alpha ^{n-1}\ge 1. \end{aligned}$$

(13)

Condition (13) sets a lower bound for $\alpha .$ In particular, if $c<1$, this implies

$$\begin{aligned} \alpha +\alpha ^{2}+\alpha ^{3}+\cdots +\alpha ^{n-2}+\alpha ^{n-1}\ge c, \end{aligned}$$

(14)

which means that no node is interested in severing the only link that it supports.

No player has an incentive to double a weak link if

$$\begin{aligned} \alpha +\alpha ^{2}+\alpha ^{3}+\cdots +\alpha ^{n-2}+\alpha ^{n-1}-c\ge 1+\alpha +\alpha ^{2}+\alpha ^{3}+\cdots +\alpha ^{n-2}-2c, \end{aligned}$$

that is, if

$$\begin{aligned} c\ge 1-\alpha ^{n-1}. \end{aligned}$$

(15)

Therefore, (13) and (15) are necessary conditions for an n-player oriented wheel to be stable. Note that the greater the number of players, the less constraining the first condition becomes and the more constraining the latter will be. In general, these conditions are not sufficient. For instance, in a wheel with enough nodes it may be advantageous for a node to initiate a link with the node furthest away: assume for instance that n is odd, i.e. $n=2m+1$ for an integer m, $N=\{i_{0},i_{1},\ldots ,i_{2m}\}$ and $g_{i_{1}i_{0}}=g_{i_{2}i_{1}}=\cdots =g_{i_{2m}i_{2m-1}}=g_{i_{0}i_{2m}}=1$. Then $i_{0}$ has no incentive to initiate a link with $i_{m}$ if

$$\begin{aligned} \alpha +\alpha ^{2}+\alpha ^{3}+\cdots +\alpha ^{2m-1}+\alpha ^{2m}-c\ge 2\alpha +2\alpha ^{2}+\cdots +2\alpha ^{m}-2c, \end{aligned}$$

that is, if

$$\begin{aligned} c\ge \alpha (1-\alpha ^{m})(\alpha +\alpha ^{2}+\cdots +\alpha ^{m}). \end{aligned}$$

(16)

Fig. 4

Oriented wheel stability: necessary conditions $(n=9$)

When the number of players increases, this and previous conditions considerably constrain the region where an oriented wheel can be stable. Part of region S below $c=1$ in Fig. 4 illustrates this for $n=9.$ Condition (13) sets a lower bound on $\alpha$, and its boundary is represented by a vertical dashed line, while the other two, (15) and (16),²¹ set lower bounds for c relative to $\alpha$. Therefore, these necessary conditions constrain the possible stability of oriented wheels to two regions within the area where $c<1$ (their boundaries are shown in thick lines on the figure): a narrow strip close to $\alpha =1$ (i.e. to Bala and Goyal’s one-way flow model), along with a small piece between (13) and (16) (there is always room between) and above (15), which as n increases shrinks to a small patch close to $(\alpha ,c)=(1/2,1)$.²²

By Corollary 2, above $c=1$ stability entails the existence of cycles. By examining the necessary conditions for an oriented wheel to be stable discussed for $c>1$ we have the following. Condition (13) sets a lower bound on $\alpha$, but it is implied by (14) when $c>1$. Thus (14) is now a stringent condition which sets an upper bound on c, whereas conditions (15) and (16), set lower bounds on c. But now (15) holds trivially (it is implied by $c>1$). Thus we are left with two necessary conditions (14) and (16), which, as part of region S above $c=1$ in Fig. 4 shows, hold in a rather wide area.

On the other hand, it is clear that as the number of players in a cycle increases new conditions of the type of (16) for a cycle forming part of a stable network will appear, and presumably more complex structures with multiple cycles may arise and prove to be stable. Nevertheless, whenever cycles are feasible characterizations are problematic and we have not been able to obtain further results.²³ Nevertheless, the following example shows that cycles are actually feasible in equilibrium.

Fig. 5

Oriented 4-node wheel stability

Example 3

If $n=4$, and g consists of 4 links: 12, 23, 34 and 41. Conditions (13) and (15) become:

$$\begin{aligned} \alpha +\alpha ^{2}+\alpha ^{3}\ge 1 \quad \text {and}\quad c\ge 1-\alpha ^{3}. \end{aligned}$$

As to condition (16), no player has an incentive to initiate a new link with the node at the opposite corner of the “square” if: $\alpha +\alpha ^{2}+\alpha ^{3}-c\ge 2\alpha +\alpha ^{2}-2c$, that is, if

$$\begin{aligned} c\ge \alpha -\alpha ^{3}. \end{aligned}$$

But this is implied by $c\ge 1-\alpha ^{3}$. In fact, it can easily be shown that if conditions (13) and (15) hold no change of strategy by a single node improves its payoff. Thus, these conditions are necessary and sufficient for the 4-node oriented wheel to be a Nash network (strict Nash if both conditions hold strictly). Pairwise Nash stability further requires that no two nodes between which no link exists benefit from creating a strong one, that is $\alpha +\alpha ^{2}+\alpha ^{3}-c\ge 1+2\alpha -2c$, or

$$\begin{aligned} c\ge 1+\alpha -\alpha ^{2}-\alpha ^{3}. \end{aligned}$$

(17)

Figure 5 shows the region ($S_{1}$ and $S_{2}$) where conditions (13) and (15) hold and the 4-node oriented wheel is Nash (strict Nash in the interior): to the right of line (13) and above curve (15). Finally, the 4-node oriented wheel is pairwise Nash stable above curve (17), thick dashed in the figure (region $S_{2}$).

6 Dynamics

Bala and Goyal (2000a) provide a dynamic model that converges to strict Nash networks for the one-way flow model without decay. They consider a sequential form of best response dynamics: in each period one player chosen at random plays a best response while all other players continue to support their links. This yields a Markov chain on the state space of all networks. They prove that this dynamic model converges to an oriented wheel, the only strict Nash architecture for the one-way flow model without decay.

We only address the question of convergence of sequential dynamics for values of the parameters within the only region where a full characterization of strict Nash profiles has been achieved, i.e. only for $c<1-\alpha$. We have the following:

Proposition 6

In the JWBG1 model, with $0<\alpha <1$ and $c<1-\alpha$, sequential best response dynamics converge to a strict Nash network with probability 1.

Given that this result (and its proof) is entirely similar to Proposition 12 in Olaizola and Valenciano (2015a), we do not repeat all the details here. The intuition of why this is so is the following. Strict Nash networks in this region are the same in both models and consist of strong links only. As commented in remark (vii) in Sect. 3, strong links are more stable in the JWBG1 model than in the JWBG2 model, while for weak links the situation is the opposite. Thus it is not surprising that the same dynamics leads to the same absorbing states. However, to ensure that the paper is basically self-contained, an informal description of the way in which a sequence of best responses is produced starting from any strategy profile that yields a strict Nash profile is given below. A natural modification of the sequential best response dynamics consistent with a scenario where pairwise coordination is possible is the following: in each period a player may either play a best response or propose the formation of a new strong link to one player. This “extended” best response dynamics ensures convergence to a pairwise Nash stable profile by merely letting players keep playing once a strict Nash profile is reached until the resulting profile is strongly-connected.

Outline of the proof of Proposition 6:

• 1. After a best response from an arbitrary node i: (1) the set of nodes in the strong component of the resulting profile containing i contains the set of nodes in the strong component containing i in the previous profile; (2) no further best response will ever break a strong link in which i is involved; (3) any weak link supported by i belongs to a different strong component [similar to Lemma 7 in Olaizola and Valenciano (2015a)].

• 2. Therefore, if after an arbitrary player plays a best response another player in the same (new) strong component plays another, after a finite number of steps all players in a strong component must be playing best responses. Then either the component is isolated or one of its nodes supports a weak link with a node j in a different strong component. In the latter case, let j play a best response and restart the sequence. In this way after a finite number of best responses an isolated strong component C is generated. [see Procedure 1 and Claim 1, in Olaizola and Valenciano (2015a)].

• 3. At the end of the sequence described in 2, there are two possible cases: either $\#C\ge c/\alpha$ or not. In the latter case, apply the sequence described in 2 starting with a node in a different strong component. Reiterate the process until a component of size $\ge c/\alpha$ is generated or, otherwise, a profile consisting of isolated strong components smaller than $c/\alpha$ is generated. In the second case, a strict Nash profile is obtained [Algorithm 1, Claim 2 in Olaizola and Valenciano (2015a)]. Otherwise proceed as follows:

• 4. If at the end of 3 a strong component greater than or equal in size to $c/\alpha$ is obtained, then it is easy to show that a sequence of best responses exists that yields a profile consisting of a unique minimally strongly-connected component, i.e. a minimally strongly-connected profile, which is strict Nash in the whole region [Lemma 8 in Olaizola and Valenciano (2015a)].

7 Conclusion

The model presented in this paper completes a “triangle” whose vertices are three benchmark models of strategic formation of networks: the no-decay version of Jackson and Wolinsky’s (1996) connections model, and Bala and Goyal’s (2000a) one-way and two-way flow models without decay. Summing up, the transition from the no-decay version of Jackson and Wolinsky’s (1996) connections model (case $\alpha =0$ in ours) to Bala and Goyal’s (2000a) one-way flow model without decay (case $\alpha =1$ in ours) has similarities with the transition to Bala and Goyal’s (2000a) two-way flow model studied in Olaizola and Valenciano (2015a), but also important differences.

In the JWBG1 model studied here, for $c<1-\alpha$ everything is entirely similar to what occurs in the JWBG2 model in Olaizola and Valenciano (2015a). In both cases, there is a smooth extension of the results in Jackson and Wolinsky’s connections model in these regions. The stability of each stable profile for Jackson and Wolinsky’s connections model without decay extends up to a point: the moment when the greatest strong component is enough to make the profile unstable. In both models, for $c<\alpha$, the only Nash, strict Nash and pairwise Nash stable profiles are those minimally strongly-connected.

By contrast, for $c\ge 1-\alpha$ results differ from those in JWBG2. In both models, only stable architectures without cycles have been characterized. In the model considered here, the line $c=1-\alpha$ has no impact on the stability of the stable structures below it, which remain stable above it. But in JWBG2 above this line peripheral players must necessarily be connected through weak links in equilibrium, giving rise to the tree-core-periphery architectures. In JWBG2 the existence of cycles in equilibrium above this line is not confirmed, while in JWBG1 their existence is established for $c<1$, and their necessity is proved for $c>1$ (Sect. 5.3). Nevertheless, no characterization has been obtained.

As to efficiency, Lemma 1 makes it possible to transfer straightforwardly to JWBG1 (Corollary 1) part of the characterizing result in JWBG2. Finally, the dynamic models discussed in Sect. 7 prove convergence to strict Nash and to pairwise Nash stable profiles in the region where the characterization of strict Nash and pairwise Nash stable profiles is complete, i.e. $0<\alpha <1,$ $c<1-\alpha$.

A criticism similar to that leveled at the model in Olaizola and Valenciano (2015a) applies here too. In one sense, although the model actually bridges the two extreme models, corresponding to $\alpha =0$ and $\alpha =1$, the intermediate model lacks symmetry. The assumption that flow through strong links is always frictionless amounts to overlapping the no-decay version of Jackson and Wolinsky’s model and Bala and Goyal’s (2000a) one-way flow model with decay.

Some issues remain open. No example of “mixed” profile, i.e. containing both weak and strong links, efficient or stable has been provided, nor has the question of their existence or non-existence been settled.

An interesting line of further research could be to parallel the study conducted in Olaizola and Valenciano (2015b), which actually bridges the gap between Jackson and Wolinsky’s (1996) connections model and Bala and Goyal’s (2000a) one-way flow model, both with decay. Note that JWBG1 is consistent with a situation in which links supported by two players transmit a fraction $\delta$ of the unit of information at each node, while links supported by only one player transmit a fraction $\alpha \le \delta$ and only towards the player that supports the link. The model developed here is a stylized version which considers $\delta =1$, that is, links supported by both players work perfectly. Another potentially interesting issue would be exploring the interior of the triangle of models represented in Fig. 1.

Beyond these possible extensions, and of a more immediate interest, is the question of the applicability of the model. In this respect, it is interesting to mention a recent work of Comola and Fafchamps (2014) where they test the true nature of links in networks based by self-reported links from survey data.²⁴ They “ propose a method for testing whether survey responses can safely be interpreted as a link and, if so, whether links are generated by a unilateral or bilateral link formation process”. They even propose a “hybrid model” for the test with an additional parameter $\delta$ to represent the extent to which each respondent internalizes the other’s desire to link in his survey response. “If $\delta$ $=1$, this boils down to the bilateral link formation model. In contrast, if $\delta$ $=0$, the second term in the right-hand side becomes a constant and the regression boils down to the desire-to-link model.” The completely different settings, one where networks are based on empirical survey data and another where networks are based on an abstract model, only make the parallelism more remarkable and gives a hint about the model’s potential.