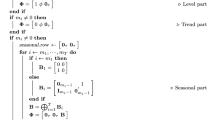Abstract
In seasonal adjustment a time series is considered as a juxtaposition of several components, the trend-cycle, and the seasonal and irregular components. The Bureau of the Census X-11 method, based on moving averages, correction of large errors and trading day adjustments, has long dominated. With the success of ARIMA modelling at the end of the 20th century, methods with better outlier detection and trading day corrections by regression with ARIMA errors have appeared, with the regARIMA module of Census X-12-ARIMA or Bank of Spain TRAMO-SEATS. SEATS consists of extracting the components by an ARIMA-model-based unobserved components approach. This means that models are used for each component such that the sum of the components is compatible with the ARIMA model for the corrected time series. The underlying theory of the SEATS program is studied in many papers but there is no complete and systematic description of its output. Our purpose is to examine SEATS text output and to explain the results in simple words and formulas. This is done on a simple example, a time series with a non-seasonal model so that the computations can be verified step by step. The principles behind SEATS are first described, including the admissible decompositions and the canonical decomposition, and the derivation of the Wiener-Kolmogorov filter. Then the example is introduced: the interest rates of US certificates of deposits. The text output from SEATS is presented in edited form in several tables. Finally, the main results are checked on the example by means of a Microsoft Excel workbook and direct computations. In particular, the forecasts and backcasts are obtained; the admissible and canonical decompositions with two components are discussed; the filters are first derived using autocorrelations of two auxiliary ARMA processes, then applied on the prolonged time series; and the characteristics of the estimates, the revisions and the growth rates are analyzed.
Similar content being viewed by others
1 Introduction
Seasonal adjustment is fundamental for the analysis and interpretation of macro-economic time series. The series is considered as a juxtaposition of several components: the trend-cycle, the seasonal component and the irregular component. A seasonally adjusted series is obtained by removing the seasonal component.
During the second half of the 20th century, the Bureau of the Census X-11 method (Shiskin and Eisenpress 1957) has dominated. It is based on a mixture of statistical techniques mainly moving averages, treatment of atypical observations and trading day adjustments. For a nice illustrated example showing the internals of X-11, see Ladiray and Quenneville (2002). An alternative approach under the form of an Excel file is available (Online Resource 1).
Statistics Canada X-11-ARIMA (Dagum 1980) has introduced autoregressive integrated moving average (ARIMA) modelling in particular to extend the series in the past and in the future in order to avoid end-adjustments in the moving averages. Census X-12-ARIMA (Findley et al. 1998) has improved on this by including a better outlier detection procedure and trading day corrections by regression with ARIMA errors, within a regARIMA module, while leaving nearly unchanged the old extraction of components by moving averages. Bank of Spain TRAMO-SEATS (Gómez and Maravall 1994, 2001a, b) has used a more powerful automatic model selection (AMS) procedure called TRAMO (Time series Regression with ARIMA noise, Missing values and Outliers), see below, before a very different signal extraction-based procedure called SEATS (Signal Extraction in ARIMA Time Series). While keeping regARIMA and the available model selection procedures, versions of X-12-ARIMA after version 0.3 have added the automdl spec based on TRAMO. Now (Time Series Research Staff 2013), the Bureau of the Census X-13ARIMA-SEATS has appeared, with few changes on regARIMA and automdl, but offering a choice between SEATS and the old X-11 decomposition procedure, with some improvements for the latter. Therefore, the paper is valid for TRAMO-SEATS but also for the SEATS part in X-13ARIMA-SEATS. It should also be valid for JDemetra+ which intends to be a re-implementation of TRAMO-SEATS and X-13ARIMA-SEATS using the same concepts and algorithms. Before going into the details, let us mention the basic ingredients of these two modules, TRAMO (or regARIMA), on the one hand, and SEATS, on the other hand.
Although TRAMO is complex and contains features which are still not always standard in statistical software packages for time series, the use of ARIMA models is now well mastered. Besides the standard ARIMA modelling stage by maximum likelihood, generally in an automated way, the following techniques are involved: regression with autocorrelated errors; treatment of extreme observations using corrections for outliers (additive outliers, level shift, and transitory change); Easter and mobile holiday’s effect and calendar effect adjustments; and treatment of missing observations. The ARIMA model will be directly used by SEATS but it serves also to extend the finite series, by computing as many forecasts and backcasts (i.e. forecasts performed backwards, also called backforecasts by Box and Jenkins in 1970, e.g. Box et al. 2008) as needed. It should be stressed that these techniques are integrated in the ARIMA modelling, although the use of a concentrated likelihood approach allows to estimate the parameters more or less separately.
The seasonal adjustment procedure derived by SEATS on the basis of the prolonged series and the model fitted is more difficult to explain, except the basic objective: a decomposition of the series a little bit like in elementary seasonal decomposition methods. However, the signal extraction procedure in SEATS is based on engineering techniques which are generally much less mastered by economists and even statisticians, with some exceptions. The underlying theory of the SEATS program is studied in many papers but there is no complete and systematic description of its output. There are a few tutorial papers, like Kaiser and Maravall (2001), but they are perhaps still too complex for the interested audience. There does not appear to be a paper showing the main concepts in a simple way. Unfortunately, even for the airline model (or an \(\hbox {ARIMA}(0,1,1){(0,1,1)}_s\) model on logarithms of the data, with s \(=\) 12 for monthly observations), the simplest realistic ARIMA model at the TRAMO or regARIMA stage, things are still too complex.
The main purpose of this paper is therefore to examine the details of SEATS text output and to explain the results in simple words and formulas. It is done on the basis of an example, with a step-by-step description of a typical output from SEATS. To keep the explanation as simple as possible, the example will not use a seasonal decomposition but will use the simpler signal extraction of a trend. The example is for a time series with a non-seasonal model so that the computations can be easily verified. Therefore the models are much simpler and fewer numbers need to be interpreted while preserving the essential. We have designed a Microsoft Excel Workbook (Online Resource 2) which shows most of the output and a document with some instructions (Online Resource 3). Using Microsoft Excel for doing statistics is not generally recommended (see the references in Mélard 2014), but it is the right tool to describe simple computations. It would be difficult to use Excel to demonstrate SEATS in a more realistic example with a seasonal component. The regARIMA or TRAMO part of the treatment are not discussed, nor the graphical output.
We have found a monthly series called TICD (also used in Mélard 2007), the interest rates of U.S. certificates of deposit, between December 1974 and December 1979, which is a non-seasonal series. We have obtained a non-seasonal but otherwise very interesting decomposition, being able to compare the results for the filter weights and most of the output with those obtained using SEATS, see Tables and Online Resource 4.
The principles behind SEATS are described in Sect. 2, including the admissible decompositions and the canonical decomposition, and a procedure to implement the derivation of the Wiener-Kolmogorov filter. In Sect. 3 the example is introduced: the time series and the text output from SEATS is presented in edited form in several tables. Finally, in Sect. 4, the main results are checked on the example by means of a Microsoft Excel workbook and direct computations. In particular, the forecasts and backcasts are obtained; the admissible and canonical decompositions with two components are discussed; the filters are first derived using autocorrelations of two auxiliary ARMA processes, then applied on the prolonged time series; and the characteristics of the estimates, the revisions and the growth rates are analyzed. We will conclude in Sect. 5. Appendix 1 will serve to introduce spectral analysis in a general approach. Appendix 2 will introduce the spectral analysis used in SEATS for the derivation of a canonical decomposition.
2 Principles behind SEATS
We will explain the principles first in informal terms and using simple models, before introducing SEATS more widely. In the next two sections we will use a simpler model by going into details first on the basis of SEATS output on the TICD series, then on the basis on an Excel file which describes the computations. As mentioned before, TICD is a non-seasonal series so that the decomposition will be simpler than with a seasonal series. We suppose we have obtained an ARIMA model for the original series or a corrected version of it, using either TRAMO or regARIMA. The corrected series will differ from the original series if the pre-treatment by TRAMO or regARIMA has detected outliers or calendar effects. In the sequel, \(y_{t}\) denotes the corrected observation at t. SEATS is aimed at decomposing the obtained ARIMA model in a sum of components and extract them from the series. There can be up to 4 components: the permanent or trend (-cycle) component,Footnote 1 the transitory component, the seasonal component, and the irregular component or error. In the majority of cases of a multiplicative mode of composition, SEATS works with an additive decomposition of the data in logarithms, \(\hbox {log}(y_{t})\). Here we will restrain ourselves to two or three components and an additive decomposition, to simplify the presentation.
For the moment, denoting the observations, \(y_{t},t=1,...,T\), we will consider the decomposition
respectively the permanent, seasonal and irregular components but on TICD we will use another decomposition. Suppose, for example, that the series is represented by some \(\hbox {ARIMA}(p, d, q)(P, D,Q)_{12}\) process, for example the so-called “airline” modelFootnote 2 (Box et al. 2008), without the logarithmic transform however,
where the \(e_{t}\)’s represent an innovation series, i.e. a sequence of innovations, independent random variables with mean zero and constant variance V, also called a white noise process. Here B is the lag operator, such that \(By_{t}=y_{t-1},\nabla =1-B\) denotes the regular difference, such that \(\nabla y_{t}=y_{t}-y_{t-1}\), and \(\nabla _{12}\) denotes the seasonal difference with period 12, such that \(\nabla _{12}y_{t}=y_{t}-y_{t-12}\). In this case, there is no need for a transitory component.Footnote 3
In the simplified case of two components
the idea of SEATS would be to find two different ARIMA models, one for \(P_{t}\) and the other for \(I_{t}\), both based on innovation sequences that are mutually independent from each other, extract these two series from the original series using these models, such that the sum of the two series \(P_{t}\) and \(I_{t}\) is identical to the given series \(y_{t}\). There is of course no reason that such a decomposition does exist, nor that it is unique. In the special case of the airline model considered here, the answer to the first question is negative because a third component should be added. This allows us to introduce the concepts of admissible decomposition and of canonical decomposition. There is an admissible decomposition if at least one decomposition does exist. If there is an admissible decomposition, there is no reason it is unique but we will describe conditions to obtain a canonical decomposition, one of those admissible decompositions which is optimal in some sense.
To be more specific, let us now consider a quarterly series with a model described by
where \(\theta (B)\) is some well specified polynomial in B, with degree \(q\le 4\),Footnote 4 and a decomposition with three components like in (2.1). Note the following factorization of the quarterly seasonal difference
where \(U_{3}(B)\) is a polynomial of degree 3 with (complex) unit roots. The innovations of the three components are supposed to be independent white noises, which will be denoted \(e_{t}^{P},e_{t}^{S}, e_{t}^{I}\). We try to impose the form of the three ARIMA models which will represent these three components. Logically, the ARIMA model for the permanent component should not have a seasonal difference since it is not supposed to show a seasonal behaviour but will show an ordinary difference and possibly two, noting (2.3). On the contrary the model for the seasonal component should at least include \(U_{3}(B)\). Finally, the model for the irregular component should show no difference at all and perhaps simply be a white noise. Let us consider the following models that satisfy these requirements:
with two MA polynomials, \(\theta _{P}(B)\) and \(\theta _{S}(B)\), which are still to be specified. We can write the first two models by moving the differences to the denominator:
so that if we write the sum of the components, with explicit appearance of the models, we obtain
Now, we can transform the right hand side by using a common denominator which is, again, using (2.3),
as expected given the model for the series, giving
which implies the relation between the four types of innovations
To exploit this, we need to consider autocovariances at some positive lags k. We have supposed that the polynomial \(\theta (B)\) has degree q. Then the autocovariances of \(\theta (B)e_{t}\) vanish for \(k>q\). Since the autocovariance of a sum of independent processes is the sum of the autocovariances of these processes, it implies that the autocovariances at lags \(k>q\) of the right hand side of (2.4) also vanish. This is a constraint on the respective degrees \(q_{P}\) and \(q_{S}\) of \(\theta _{P}(B)\) and \(\theta _{S}(B)\), since the degrees of \(\theta _{P}(B)(1+B+B^{2}+B^{3})\) and \(\theta _{S}(B)(1-B)^{2}\) are to be less or equal to \(q: q_{P}+3\le q\) and \(q_{S}+2\le q\). Moreover, relations between the coefficients of the three polynomials \(\theta (B), \theta _{P}(B)\) and \(\theta _{S}(B)\) can be deduced from equality of \(q+1\) autocovariances at lags 0 to q. There is no reason why the number q of coefficients of \(\theta (B)\) would be less or equal the number \(q_{P}+q_{S}\) of unknown coefficients of \(\theta _{P}(B)\) and \(\theta _{S}(B)\). This can be seen in this special case as a condition for admissibility of a decomposition. More precisely, a particular point of attention consists in obtaining the innovation standard deviations of each of the components, which of course need to be strictly positive. This will be illustrated in Sect. 3.2. SEATS does not use that approach but rather a spectral approach which is too complex for this presentation, see however Appendix 2.
Moreover, even if we can determine the \(q_{P}+q_{S}\) of unknown coefficients, there is no reason why that solution would be unique. In other words, if there exists an admissible decomposition, we need to determine what is called a canonical decomposition. A detailed examination of these two problems of admissible and canonical decompositions are outside the scope of this paper and has been solved elsewhere (Hillmer and Tiao 1982; Maravall and Planas 1999; Fiorentini and Planas 2001). In Sect. 3 we will merely illustrate these problems on the example of a model for TICD. More precisely, after having determined a collection of admissible decompositions, we will select the canonical decomposition within that collection. We will not discuss other related problems such as the possible need to change the model for the corrected series in order to be able to perform the decomposition; the specification of the models for the components; the selection of the number of components; and the diagnostics surrounding the decomposition. Some of these problems will however be mentioned while looking at the example.
Assuming we have obtained the models for the components, there remains to implement the decomposition, i.e. to construct the component series. This is the problem of signal extraction or the design of a filter. Typically, these component series’ will be built as moving weighted averages of the observations of the corrected series duly extended in both directions by forecasts and backcasts. We have denoted by \(y_{t}\) the observation at time \(t, t=1,..., n\). Let  , and the forecasts for \(t>n\), and the backcasts for \(t<1\). We have mentioned the Census X-11 method in Sect. 1. Several authors (Cleveland and Tiao 1976) have investigated how the many simple and weighted moving averages applied to the data contribute there to define a filter. As they have shown, under some simplifying assumptions, that filter subsumes a particular ARIMA model for the data, so that the same filter is applied whatever the series, except for the selection of some options (e.g. the orders of the Henderson moving averages for obtaining the trend-cycle or the orders of the moving averages across years). The principle of SEATS is to use the model for the series and the models for the components to derive a filter with coefficients \(\nu _{j}\). In our example with three components \(P_{t}, S_{t}\), and \(I_{t}\), we would have three sets of filter with respective coefficients \(\upsilon _{j}^{P}\). \(\upsilon _{j}^{S}\). and \(\upsilon _{j}^{I}\). Hence, the estimates of the components would be
, and the forecasts for \(t>n\), and the backcasts for \(t<1\). We have mentioned the Census X-11 method in Sect. 1. Several authors (Cleveland and Tiao 1976) have investigated how the many simple and weighted moving averages applied to the data contribute there to define a filter. As they have shown, under some simplifying assumptions, that filter subsumes a particular ARIMA model for the data, so that the same filter is applied whatever the series, except for the selection of some options (e.g. the orders of the Henderson moving averages for obtaining the trend-cycle or the orders of the moving averages across years). The principle of SEATS is to use the model for the series and the models for the components to derive a filter with coefficients \(\nu _{j}\). In our example with three components \(P_{t}, S_{t}\), and \(I_{t}\), we would have three sets of filter with respective coefficients \(\upsilon _{j}^{P}\). \(\upsilon _{j}^{S}\). and \(\upsilon _{j}^{I}\). Hence, the estimates of the components would be

where the sums extend over the prolonged part of the series in both directions. For obtaining these filters, several approaches have been introduced in the engineering, statistical and econometric literature: the so-called Wiener-Kolmogorov filter (Whittle 1983) for doubly infinite series, Kalman filtering or penalized least-squares directly for finite series. There were some difficulties to use them outside the context of stationary processes but these were solved (Bell 1984). Moreover, Gómez (1999) has shown the equivalence of the three approaches of Wiener-Kolmogorov filter, Kalman filtering, penalized least-squares. See also Pollock (2002).
Since Burman (1980), several algorithms have been designed to improve the end effects. Several authors, like Maravall (1994) and McElroy (2008), have mentioned a link with the autocovariance function of some auxiliary processes based on the innovations of the corrected series, and on the polynomials of the ARIMA models of the corrected series and of the components. These autocovariances can be computed by a straightforward algorithm (McLeod 1975) of solving a linear system of equations or by fast algorithms due to Tunnicliffe Wilson (1979) or Demeure and Mullis (1989). These simple approaches do not appear often in the literature (e.g. Gómez 1999) although Burman (1980) already mentions developments by Tunnicliffe Wilson (1979).
To illustrate this, let us suppose some ARIMA model for the corrected series. In what follows, we will not distinguish the differences, ordinary or seasonal, and the autoregressive polynomials. Instead of writing an ARIMA process under the form \(\nabla ^{d}\phi (B)y_{t}=\theta (B)e_{t}\), we write \(\varphi (B)y_{t}=\theta (B)e_{t}\), where \(\varphi (B)=\nabla ^{d}\phi (B)\) is sometimes called the generalized autoregressive operator. It can include factors of difference operators (like \(U_{3}(B)\) above). Denote V, the variance of the innovations \(e_{t}\). Suppose also that the model for the permanent component, \(P_{t}\), is written similarly \(\varphi _{P}(B)P_{t}= \theta _{P}(B)e_{t}^{P}\), where the \(e_{t}^{P}\)’s are the innovations of the permanent component. Denote \(V_{P}\) its innovation variance. Similarly, suppose that the irregular component \(I_{t}\) is written \(\varphi _{I}(B)I_{t}=\theta _{I}(B)e_{t}^{I}\), where the \(e_{t}^{I}\)’s are the innovations of the irregular component and denote \(V_{I}\) its innovation variance. Then, denoting simply \(\nu _{j}\) the coefficients in (2.5) instead of \(\upsilon _{j}^{P}\), the filtered permanent component looks like

We need to determine those weighting coefficients \(\nu _{i}\) of an unlimited moving average such that it approximates the permanent component as sufficiently as possible (in a mean square sense). By using again the lag operator B, we write the operator

Contrarily to \(\phi (B)\), for example, which is a polynomial because only the positive powers of B appear, the operator \(\nu ^{P}\) \((B,B^{-1})\) includes lags B but also leads \(B^{-1}\). This is the starting point of the Burman (1980) approach but since it is heavily spectral-oriented, we will describe it in Appendix 2. Let us denote \(p_{t}\) the least squares estimator of \(P_{t}\), such that the covariances between \(p_{t}-P_{t}\) and \(y_{t-i}\) are zero for all i. We can write it formally:
Since \(\varphi (B)=\varphi _{P}(B)\varphi _{I}(B)\), provided that \(\varphi _{P}(B)\) and \(\varphi _{I}(B)\) do not have common roots, it appears that the coefficients \(\nu _{i}^{P}\) of \(B^{-1}\) and B of the operator \(\nu ^{P}(B, B^{-1})\) are simply the autocovariances of the auxiliary process \(z_{t}\) defined by the following equation
where the \(u_{t}\) consist of a white noise process with variance \(V_{P}{/}{V}\).Footnote 5
An essential part of SEATS is the distinction between different estimators of component i at time \(t, y_{it}\). Again assume the data are \(y_{t}, t=1, ..., n\). These estimators are conditional expectations \(E(y_{it}{\vert }y_{1}, ...y_{n})\), denoted \(\hat{y}_{it|n}\). For a large enough series and values of t not close to 1 or n, they are the final or historical estimators, denoted \(\hat{y}_{it}\). In practice it occurs when \(k=n-t\) is large enough. For \(t=n\), the concurrent estimator is obtained. When \(n-k<t<n\), we have a preliminary estimator, and of course for \(t>n\), a forecast. A part of the output is devoted to the three differences, \(y_{it}-\hat{y}_{it}, y_{it}-\hat{y}_{it|n}\), and \(\hat{y}_{it}-\hat{y}_{it|n}\), which are called, respectively, the final estimation error, the preliminary estimation error and the revision error in the preliminary estimator.
3 Example of a simple case of signal extraction
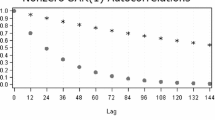
It is time to introduce the series of the interest rates of U.S. certificates of deposit, between December 1974 and December 1979, hence the length of the series is \(T=61\), see Fig. 1.
3.1 ARIMA modelling
Like most financial time series, it is non seasonal. A non seasonal ARIMA(0,1,1) modelFootnote 6 is easily obtained by TRAMO
with variance \(V=0.2332\) and \(\theta =0.4995\). We fall in a particular case of a theoretical example, random walk plus white noise, used by Pierce (1979), but our treatment is more general than in Maravall (1986), Gómez and Maravall (2001b) and others.Footnote 7 Let us skip the output of TRAMO and the summary part of the output of SEATS. We will now comment on the editedFootnote 8 output of SEATS identified by encircled numbers, starting with Table 1.
-
1.
This point shows information about the program (SEATS), about the series (TICD) and the estimation method used (exact maximum likelihood). Then the data is shown.
-
2.
The input parameters are recalled. We have used the following input parameters in TRAMO: LAM = 1 (to avoid a logarithmic transformation), RSA = 3 (for automatic model identificationFootnote 9). Note that RSA appears as being 0 in SEATS output.
-
3.
The recommended specification is to use a regular difference and no seasonal difference. The differenced series is however omitted here.
-
4.
The first twelve autocorrelations of the differenced series are displayed. They show a truncation pattern after lag 1, which confirms the model (3.1).
Table 2 presents the edited model and diagnostic statistics. Note that the output is also heavily edited.
-
5.
The final value of the (unique) estimated parameter of the ARMA model is equal to 0.4995. A more accurate value 0.499479 shown only in TRAMO output will be used in the computations of Sect. 4. The standard errors and Student statistics are not shown by SEATS but by TRAMO, where the corresponding parameter is denoted “TH1”.
-
6.
The residuals of the fitted model are displayed. They will be used in Sect. 4.1 for the computation of the forecasts.
-
7.
Some of the tests statistics on the residuals are shown, including the mean (which is not significantly different from 0, according to the t statistic). We will use the residual standard deviation, 0.4829, and its square 0.2332, the residual variance, denoted V in Sect. 2.
-
8.
Some of the additional tests are shown, such as a test for residual seasonality and the Ljung-Box test based on the 24 first residual autocorrelations.
-
9.
The backward residuals of the fitted model are displayed. They are the residuals when time is reversed, going from the future to the past. They will be used in Sect. 4.1 for the computation of the backcasts.
We will first discuss a non-seasonal but otherwise very interesting decomposition in Sect. 3.2 using the principles in Sect. 2. Then we will compare the results for the filter weights in Sect. 3.3 and most of the remaining output in Sects. 3.4 to 3.7. In Sect. 4 we will compare the results with those obtained using Excel.
3.2 Admissible and canonical decompositions
We consider a decomposition with permanent and irregular components
where the two components, permanent \(P_{t}\) and irregular \(I_{t}\), are to be modelled. As explained in Sect. 2, it is requested that the models of the two components are compatible with the model retained for TICD. As before we denote respectively \(e_{t}^{P}\) and \(e_{t}^{I}\) the innovations of the two processes for the permanent and irregular components and \(V_{P}\) et \(V_{I}\), their respective variances. A first suggestion would be to take
Let us examine if these representations are compatible with the model for TICD. Indeed, we can first write
hence \(\nabla \hbox {TICD}_{t}\) should correspond to \(e_{t}^{P}+e_{t}^{I}-e^{I}_{t-1}\). The autocovariances of a sum of independent random variables are the sum of the autovariances of these variables. We will use these properties to evaluate the autocovariances of a MA(1) process. Thus, we have:
and the autocovariances with lags larger than 1 are zero. This result is thus compatible with the process of \(\nabla \hbox {TICD}_{t}\) which is a MA(1) process. This allows to obtain the two variances \(V_{P}\) and \(V_{I}\) by equating the expressions of the variance and the autocovariance of delay 1 of \(\nabla \hbox {TICD}_{t}\). The variance of \(\nabla \hbox {TICD}_{t}\) equals \((1+ \theta ^{2})V=(1+(0.4995)^{2})\times 0.2332=0.2914\). The autocovariance at lag 1 equals \(\theta V=0.4995\times 0.2332=0.1165\). By solving the system of two equations, as we will check in Sect. 4.2, we find \(V_{I}=-0.1165\) and \(V_{P}=0.2914-2V_{I}=0.2914+2\times 0.1165=0.5244\). This system of equations does not have a satisfactory solution because a variance cannot be negative. We have to search for another admissible decomposition. We have mentioned that SEATS makes use of a spectral approach due to Burman (1980), discussed briefly in Sect. 4.2, and more deeply in Appendix 2. We will nevertheless follow our pure time-domain approach.
The following models for the components are also compatible with the model for TICD:
where \(\theta _{P}\) is a parameter, possibly subject to constraints. Indeed, as done in Sect. 2, we can use \(\nabla \) as common denominator and then consider the two polynomials in the numerators \(1+\theta _{P}B\) and \(\nabla =1-B\), both polynomials of degree 1. Therefore, the autocovariances of the sum \((1+\theta _{P}B)e_{t}^{P}+(1-B)e_{t}^{I}\) vanish for lags greater than 1, like those of the right hand side of (3.1). It will be shown in Sect. 4.2 that the canonical decomposition corresponds to the choice \(\theta _{P}=1\). Hence the models for the two components are
Table 3 presents the models of the components. Again the output is edited by omitting irrelevant items (e.g. the seasonal component).
-
10.
The second part of the output is entitled “Derivation of the models for the components”. Each polynomial of the model for the corrected series is first recalled. Here, we have here only one non trivial polynomial, the regular moving average polynomial denoted Theta: \(\theta (B)=1+0.50B\). It is given with more significant digits, like in (3.1), a few lines below.
-
11.
The new section is about the factorization of the (generalized) autoregressive polynomial, i.e. \(\varphi (B)\). Here it is \(\nabla =1-B\) and thus the factorization is trivial. We have only given the total autoregressive polynomial subsection.
-
12.
The model allows a decomposition which would have not been possible in some cases.
-
13.
The derivation of the model for each component is detailed, starting with the trend-cycle component, referred to here as the permanent component. We see that the numerator of the model for that component is \(1+B\), confirming that \(\theta _{P}=1\) was retained for the canonical decomposition, see (3.5).
-
14.
It is followed by the irregular component.
-
15.
In our case, the seasonally adjusted component corresponds to the original series. Logically its model should be identical to the global model.
-
16.
Note that all variances are expressed in proportion to the global model innovation variance V.Footnote 10 The effective variances of the two component models are respectively \(V_{P}=0.1311\) and \(V_{I}=0.01461\).
3.3 Moving average representation and Wiener-Kolmogorov filters
We have omitted the part called “ARIMA model for estimators” since there is no new piece of information. The next subsection of the output is about the moving average representation and the so-called \(\psi \)-weights and the Wiener-Kolmogorov filters for each of the components, shown in Table 4; the contribution of original series and of its innovations to the estimation of the components (omitted); the characteristics of the theoretical components, their estimators and their estimates.
-
17.
An explanation that will be commented at the end of Sect. 4.4.
-
18.
The infinite moving average representation of the component estimators, also called \(\psi \)-weights, are given here in terms of the innovations (here only for lags \(-\)10 to 2, the remaining ones being uninformative). We will give more details in Sect. 4.4.
-
19.
It is first confirmed that the filters could be derived.
-
20.
The weights of the Wiener-Kolmogorov filters for each of the components are given but only for one side since they are symmetric, and only the lags 0 to 12, the remaining entries being 0 to 4 decimal places. This does not mean that they are negligible, as will be seen in Sect. 4.4.
3.4 Distinction between theoretical components, their estimators and estimates
Still in the second section of the output, we have (see Table 5).
-
21.
The contribution of the original series and of its innovations to the estimator of the components for the present period. In the column “observation”, it is the weight of the Wiener-Kolmogorov filters (for lags 0 and 1) given in item 18. In the column “innovation”, it is the \(\psi \)-weight (for lags 0 and \(-\)1) given in item 20.
-
22.
In a subsection entitled “Distribution of component, theoretical estimator and empirical estimate”, the autocorrelation characteristics of the theoretical trend-cycle component, its estimator and its estimate, after transformation for achieving stationarity, are given. These results will be discussed and checked in Sect. 4.5. We have omitted the seasonally adjusted component which has no meaning here.
-
23.
It is followed by the autocorrelation characteristics of the theoretical irregular component, its estimator and its estimate. These results will be commented in Sect. 4.5. The error on Vis repeated here.
We have also (see Table 6)
-
24.
The cross-correlations, without any lag, between the estimators and the estimates of the two components are given here. See Sect. 4.5.
-
25.
Tests of comparisons between the estimators and the estimates according to several criteria: the variance, autocorrelation of order 1 and 12, and cross-correlation. See Maravall (2003).
-
26.
Under the heading “Weights”, the weights for the asymmetric filter for the trend given a semi-infinite realization are given. They are identical to the \(\psi \)-weights for the trend, already shown in item 18.
Several pieces of output have been deleted (phase diagram, seasonal diagnostics, the conclusions of the spectral diagnostics, the residual stochastic seasonality spectral evidence, and the trading day effect).
3.5 Error analysis
This is the third part from the output, see Table 7 for the beginning.
-
27.
It is started with the final estimation error, the only one that counts for an observation near the middle of the series, and the revision error, which is due on the arrival of a new observation.
-
28.
Under the heading “Total estimation error (concurrent estimator)” the output contains the sum of the two preceding errors. The variance is thus the sum of the two variances. For the autocorrelations, see Sect. 4.6.
-
29.
The item called “Variance of the revision error” contains the variance of the revision error after additional time has passed.
-
30.
Under the heading “Percentage reduction in the standard error of the revision”, the output contains the percentage of reduction of the variance of the revision error after additional time has passed.
The contents will be checked in Sect. 4.6. The following is in Table 8:
-
31.
The item entitled “Decomposition of the series: recent estimates”, contains the values of the components (which are also repeated further) but also their standard deviations.
-
32.
Under the heading “Decomposition of the series: forecasts”, the output contains the forecasts that can be made for each component with their standard deviations.
Details are checked in Sect. 4.1. We have omitted the “Sample means” item.
3.6 Estimates of the components
This is the fourth part from the output, see Table 9. The original series is omitted as well as the standard error of the trend-cycle. There remains:
-
33.
The trend-cycle component estimates,
-
34.
The irregular component estimates.
These series will be checked in Sect. 4.4.
3.7 Rates of growth
The fifth part of the output, entitled “Rates of growth” provides here growths since the model is applied on the data, not on their logarithms, see Tables 9, 10 and 11.
-
35.
Period-to-period growth estimation error variance for the concurrent estimator,
-
36.
Period-to-period growth for the most recent periods for the original series and the trend (with standard error of revision for the latter),
-
37.
Accumulated growth during the present year for the original series and the trend (with standard error of revision for the latter),
-
38.
Annual growth estimation error variance for the concurrent estimator,
-
39.
Annual growth for the most recent periods for the original series and the trend (with standard error of revision for the latter),
-
40.
Annual centred growth with 6 observed periods and 6 forecasts,
-
41.
Growth forecasts for the original series and the trend, with standard error of revision.
These results will be checked in Sect. 4.7.
4 Verification of the results in the example
It is clear that TRAMO-SEATS is a complex piece of software. If the basic theory is given in a few papers (Gómez and Maravall 1994, 2001a, b, and others), and can be checked empirically, some of the more sophisticated features like the selection of the canonical decomposition, the derivation of the Wiener-Kolmogorov filters, revisions, and the various diagnostics are more difficult to grasp. We will therefore describe their use on the same example as in Sect. 3, but this time with the help of an Excel file (Online Resource 2).Footnote 11 These results can then be compared with the edited output from the program in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 or with the full output (Online Resource 4). At some places simple algebraic computations are also used.
4.1 Forecasts and backcasts of the series
Before looking at decompositions, let us look at the forecasts and backcasts of the TICD series that will be needed. In the Excel file, worksheet Main, we have used the example based on the model (3.1) for TICD.
Let us first show how to evaluate the forecasts for the future months, with December 1979 as forecast origin. (3.1) implies that \(\hbox {TICD}_{t}=\hbox {TICD}_{t-1}+e_{t}+0.4995e_{t-1}\), hence the forecast at time \(T+1\) equals: \(\hbox {TICD}^{*}_{T+1}=\hbox {TICD}_{T}+0.4995e_{T}\). The next forecasts are \(\hbox {TICD}^{*}_{T+2}=\hbox {TICD}^{*}_{T+1}, \hbox {TICD}^{*}_{T+3} =\hbox {TICD}^{*}_{T+2}\), and so on. The residuals are obtained starting from the same model \(\nabla \hbox {TICD}_{t}=e_{t}+0.4995e_{t-1}\), by writing \(e_{t}=\nabla \hbox {TICD}_{t}-0.4995e_{t-1}\) where the cell V49 contains the moving average coefficient 0.4995. The data of November 1979 and December 1979 are equal to 13.97 and 13.42, respectively, and the residual in December 1979 equals \(-\)0.2863 (cell U113 which corresponds to the last number of item 6 in Table 2). Then \(\hbox {TICD}^{*}_{T+1}=13.42+0.4995\times (-0.2863)=13.28\), hence \(\hbox {TICD}^{*}_{T+2} =\hbox {TICD}^{*}_{T+3}=13.28\), and so on, see cells V114 to V131. This is shown in item 32, column “Series Forecast”, in Table 8. The computation of the forecast standard errors for the series is classic using the so-called \(\psi \) weights of the pure moving average representation of the process. Given that these weights are \(\psi _{j}=1+{\theta }\), these standard errors for horizons 1, 2 and 3 are the square roots of V, \(V(1+(1+ {\theta })^{2}), V(1+2(1+ {\theta })^{2})\), and so on. This gives the values shown in the range X114 to X125 of the worksheet and in column “Series S.E.” of item 32 in Table 8. Note that the derivation of the other columns of item 32 is differed to Sect. 4.6.
Similarly, the backcasts are obtained in reversed time, with December 1974 as forecast origin. (3.1) is an invertible model which implies that we have the following model in reverse time: \(\hbox {TICD}_{t}-\hbox {TICD}_{t+1} =u_{t}+0.4995u_{t+1}\), where we will denote \(u_{t}\) the innovations in reverse time. This implies that \(\hbox {TICD}_{t}= \hbox {TICD}_{t+1}+u_{t}+0.4995u_{t+1}\), thus the forecast at time 0 equals: \(\hbox {TICD}^{*}_{0}=\hbox {TICD}_{1}+0.4995u_{1}\). The preceding forecasts are \(\hbox {TICD}^{*}_{-2}=\hbox {TICD}^{*}_{-1}=\hbox {TICD}^{*}_{0}\), and so on. The residuals in reverse time are obtained from \(\hbox {TICD}_{t}-\hbox {TICD}_{t+1}=u_{t}+0.4995u_{t+1}\), by writing \(u_{t}=\hbox {TICD}_{t}-\hbox {TICD}_{t+1}-0.4995u_{t+1}\), where cell V49 contains the moving average coefficient 0.4995. The data of December 1974 and January 1975 are equal to 8.82 and 7.42, respectively, and the residual in December 1974 is equal to 0.9990 (cell Y53 which corresponds to the first number of item 9 in Table 2). Then \(\hbox {TICD}^{*}_{0} =8.82+0.4995\times (0.9990) =9.32\), hence \(\hbox {TICD}^{*}_{-1}=\hbox {TICD}^{*}_{-2}=9.32\), and so on, see cells AA41 to AA52. The whole series of backward residuals is shown in SEATS output, see Table 2, item 9.
4.2 Admissible and canonical decompositions
In Sect. 3.2, we have seen a general form for the difference of the permanent or trend component given by \(\nabla P_{t}=(1+\theta _{P}B)e_{t}^{P}\). We have obtained a system of two equations in the variances of the innovations of the two components \(V_{P}\) and \(V_{I}\). This system can be solved for any value of \(\theta _{P}\) between \(-\)1 and 1. In the Excel file, worksheet Second, we have used the context of the example based on the TICD model. We have entered in cells B9 and B10 the value of \(\theta \) and V, respectively. In cells A15 to A35, we have placed potential values of \(\theta _{P}\) between \(-\)1 and 1. In the next two columns formulas give the solutions of \(V_{P}\) and \(V_{I}\). in function of \(\theta _{P}\). The resulting table is copied in Table 12. We can see that not only \(\theta _{P}=0\) is not admissible, because one of the two variances is negative, but also that only values of \(\theta _{P}\) between 0.6 and 1 lead to admissible decompositions. There remains to justify why the canonical decomposition should be the one corresponding to \(\theta _{P}=1\).
4.3 The canonical decomposition
To justify the selection of a canonical decomposition among the admissible decompositions, we need to define a criterion. Several criteria can be developed but we use two of them.
We saw that an admissible decomposition is generally not unique. It is here that the interpretation of the models for the components intervenes. In the example, the two components are the permanent component and the irregular component. We should impose that the permanent component is as smooth as possible, thus free from irregularities. This means that we must assign all the irregularities to the irregular component. In statistical terms, we require that the variance of the irregular component be maximum. The criterion we will use is thus to maximize that variance \(V_{I}\). By inspecting Table 12, we see that the variance of the irregular component depend on \(\theta _{P}\), and that the maximum is reached for \(\theta _{P}=1\). This is precisely the decomposition that we have observed in the output of SEATS in Table 3. Note that we have then the identity
Another approach is provided by spectral analysis that we recall in Appendix 1 (see Priestley 1981 for alternative approaches). There we define the spectrum (or spectral density) of a stationary process and the pseudo-spectrum of a non-stationary process. The spectrum of a stationary process describes the distribution of the variance of the process according to the frequencies and is therefore everywhere non-negative. Note that the generalized spectrum of a non-stationary process cannot be interpreted in the same manner because the variance does not exist. The spectrum of a sum of independent random processes is equal to the sum of the spectra. We can thus break up the pseudo-spectrum of the process TICD into the sum of the spectra of the permanent and irregular components. In the Excel file, worksheet Second, we can check on the example, by changing the MA coefficient in cell G12 so that the canonical decomposition corresponds to the case where the minimum of the spectrum of the permanent or trend component is equal to 0, see Fig. 2. This is for \(\theta _{P}=1\), of course. The different columns in the range E11 to O160 contain the Excel formulas for the computations of the spectrum based on the model (3.1), i.e. (A1.5) in Appendix 1. Note that these computations use complex numbers instead of real numbers so that even additions need a specific function IMSUM (in the English version of Excel) instead of the usual + operator. The other functions needed (again in the English version) are IMPRODUCT for a product, IMPOWER for a power, and IMABS for a modulus. The spectra for the trend and for the irregular models are similarly shown in the ranges Q11 to Y160 and AA11 to AA160, respectively. The results for the three spectral densities are then shown in a plot contained in the sheet Spectrum. It is for the value \(\theta _{P}=1\) that the spectrum of the irregular component is the highest. It cannot increase any further because it would exceed the spectrum of the sum.
4.4 Moving average representation and Wiener-Kolmogorov filters
It is easier to present the derivation of the components using the Wiener-Kolmogorov filters before discussing the moving average representation.
In our example of extraction of the permanent component, the theory in Sect. 2 and (2.7) yields that the estimator \(p_{t}\) of \(P_{t}\) can be expressed by \(p_{t}=\nu ^{P}(B, B^{-1})y_{t}\) or
after cancellation of \(1-B\), and that the auxiliary process (2.8) is a stationary ARMA(1, 1) process defined by
where the \(u_{t}\) consist of a white noise process with variance \(V_{P}/V=0.1311/0.2332=0.5622\), contained in cell D47 of worksheet Main. To compute the weights of the Wiener-Kolmogorov filter, we need to compute the autocovariances of that auxiliary process. We have used that for an ARMA(1, 1) process defined by the equation \((1+\phi B)z_{t}=(1+ \theta B)u_{t}\), we have (e.g. Box et al. 2008, Section 3.4.3) the autocovariances \(\gamma _{k}\) are given by:
and \(\gamma _{2}=-\phi \gamma _{1}\), \(\gamma _{3}=-\phi \gamma _{2},\ldots \) The formulas are applied in worksheet Main in cells AA8 to AA32. It will be useful for the sequel to provide the specific formulas for the Wiener-Kolmogorov weights \(\nu _{j}^{P}\) of \(B^{-1}\) and B of the operator \(\nu ^{P}(B, B^{-1})\). They are obtained by replacing in (4.4) \(\theta \) by 1 and \(\phi \) by \(\theta \):
The extraction of the irregular component can be done in a similar way. Thus, in our example, its estimator \(i_{t}\) of \(I_{t}\) can be expressed by \(i_{t}=\nu ^{I}(B, B^{-1})y_{t}\) and is equal to
and the auxiliary process is a stationary ARMA(1,1) process defined by
where the \(v_{t}\) consists of a white noise process with variance \(V_{I}/V=0.01461/0.2332=0.06263\), contained in cell E47 of worksheet Main. Note that only the sign of the MA coefficient differs from the case of the permanent component. The formulas are applied in worksheet Main in cells AB8 to AB32. The two sets of weights of the Wiener-Kolmogorov filters are shown in Fig. 3 (from the worksheets WTS_TRD and WTS_IRR). Note also that \(\nu ^{P}(B, B^{-1})+\nu ^{I}(B,B^{-1})=1\).
We can now use the two filters to extract the components. To see the calculation of the components for the permanent and for the irregular component, we have applied the weighted moving averages in Fig. 3 to the series prolonged with forecasts and backcasts. This is done in the Excel file, worksheet Main in the range AB53 to AB113 for the permanent component and in the range AC53 to AC113 for the irregular component. To achieve the accuracy for the components shown in Table 9 of the SEATS output, we have made a correction to take care of a few more weights. Nevertheless, there are some differences for the irregular component.Footnote 12
Now we are able to examine the moving averages representations and in particular the \(\psi \)-weights that precede the filters in the output. They are obtained by replacing the observations in (4.2) and (4.6) above in function of the innovations. Since future observations are used as well as past observations, the expressions make use of past but also of future innovations. Therefore we have for the estimator of the permanent component
and for the irregular component
After some algebraic calculations, we obtain for \((1-B)\) times the fraction in (4.7)
These coefficients for \(\theta =0.4995\) are computed in worksheet Main, in the range AY1 to BQ20. Multiplying (4.9) by \((1-B)^{-1}\) gives
hence \(1.667+(2.667B+2.667B^{2} +2.667B^{3}+{\cdots })+(0.167B^{-1}-0.083B^{-2}+0.042B^{-3}-{\cdots })\), see range BS50 to BW60, and by multiplication by \(V_{P}/V=0.5622\):
This (formal) power series expansion is denoted \(\xi (B,B^{-1})\) in Gómez and Maravall (2001b), such that \(p_{t}= \xi (B, B^{-1})e_{t}\). In Sect. 4.6 we will need the coefficients \(\xi _{j}\) of \(B^{-j}\) for \(j>0\) which are given by
hence \(\xi _{1}=0.094\). We will also need the coefficient of B and the constant which are thus numerically equal to \(\xi _{-1}=1.499\) and \(\xi _{0}=0.937\). Note that (4.10) can be obtained more elegantly from (4.7) using a partial fraction expansion, like in Burman (1980) approach (see Appendix 2):
which gives after identification of the terms in the numerator and solving a linear system of equations: \(\alpha _{0}=0.9375, \alpha _{1}=0.5997\), and \(\beta _{0}=0.0939\).
We can proceed in the same way, but more simply, for the estimator of the irregular component: the fraction on the right hand side of (4.8) is
hence
These coefficients are computed in worksheet Main, in the range AY24 to BQ42. They can be found in the output, located at item 18 in Table 4, more precisely in columns 2 (PSIEP) and 6 (PSIUE). The sum of the columns 2, 3, 5 and 6 (not column 4, contrarily to what is said in the output; this is corrected in revision 935) gives the coefficient of the moving average of the process defined by (3.1), i.e. 0 for strictly negative lags, 1 for lag 0, and 1 + 0.4995 for strictly positive lags. Like the Wiener-Kolmogorov coefficients \(\nu _{j}^{P}\) represent the contribution of \(y_{t-j}\) to the estimator of the permanent component, the coefficients in (4.10) represent the contribution of the innovations \(e_{t-j}\) to that estimator.
4.5 Autocorrelations of the components, the estimators and the estimates
It is specified in the output (see Table 5) that what is shown is the autocorrelation function of a “stationary transformation of components and their estimators”. We first check the components and the estimates, before the estimators which are more complex to handle.
We have already specified the processes for the two components. The process for the permanent component \(P_{t}\) is non-stationary. Therefore what is shown is the autocorrelation function of the difference of the process, i.e. \(\nabla y_{t}\). Since that process is MA(1) with coefficient 1, the first-order autocorrelation is equal to 0.5 and the other autocorrelations are equal to 0. This is shown in the second column of item 22 in Table 5. The Excel file, sheet Main (range AF51 to AM121), shows the computation of the first three autocorrelations for the estimate  of the permanent component \(P_{t}\) detailed in Sect. 4.4: 0.539, 0.023, \(-\)0.051. See cells AI121, AK121 and AM121. They agree with item 22 in Table 5, column “Estimate”. Computing the autocorrelations of the estimator \(p_{t}\) defined by (4.7) in function of the innovations of the process defined by (3.1) is more complex. The coefficients of the moving average representation for \(\nabla p_{t}\) have already been found in (4.9) up to a factor \(V_{P}/V\). To evaluate the variance, we have to take the sum of the squares of these coefficients given by \(1+(2-\theta )^{2}+(1- \theta )^{4}/(1-\theta ^{2})\), and multiply it by \((V_{P}/V)^{2}\). This yields 1.054, as indicated by item 22 in Table 5, on the line “VAR” and in cell AZ22, or 0.24575 in original units, see cell BA22. The autocovariances are computed in worksheet Main, in the range BS1 to DC19. Dividing them by the variance located in cell AZ21, we obtain the autocorrelations displayed in cells DD4 to DD19, e.g. 0.5501 for lag 1. They correspond to the contents of SEATS output, item 22 in Table 5, column “Estimator”. The variance in units of V is in cell AZ22.
of the permanent component \(P_{t}\) detailed in Sect. 4.4: 0.539, 0.023, \(-\)0.051. See cells AI121, AK121 and AM121. They agree with item 22 in Table 5, column “Estimate”. Computing the autocorrelations of the estimator \(p_{t}\) defined by (4.7) in function of the innovations of the process defined by (3.1) is more complex. The coefficients of the moving average representation for \(\nabla p_{t}\) have already been found in (4.9) up to a factor \(V_{P}/V\). To evaluate the variance, we have to take the sum of the squares of these coefficients given by \(1+(2-\theta )^{2}+(1- \theta )^{4}/(1-\theta ^{2})\), and multiply it by \((V_{P}/V)^{2}\). This yields 1.054, as indicated by item 22 in Table 5, on the line “VAR” and in cell AZ22, or 0.24575 in original units, see cell BA22. The autocovariances are computed in worksheet Main, in the range BS1 to DC19. Dividing them by the variance located in cell AZ21, we obtain the autocorrelations displayed in cells DD4 to DD19, e.g. 0.5501 for lag 1. They correspond to the contents of SEATS output, item 22 in Table 5, column “Estimator”. The variance in units of V is in cell AZ22.
The process for the irregular component \(I_{t}\) is stationary. Therefore a difference is not needed to make it stationary and all autocorrelations are equal to 0 for strictly positive lags. This is shown in the second column of item 23 in Table 5. The Excel file, sheet Main, range AP51 to AW121, shows the computation of the first three autocorrelations for the difference of the estimate \(\hat{\imath }_{t}\) of the irregular component \(I_{t}\) detailed in Sect. 4.4: \(-\)0.766, 0.421, \(-\)0.229, in cells AS121, AU121 and AW121. They agree nearly perfectly with item 23 in Table 5, column “Estimate”, where the respective results are \(-\)0.765, 0.421, \(-\)0.229. This discrepancy can be explained by the relatively small number of exact significant digits for the irregular estimates. Even if the autocorrelations for the estimates are not too far from the autocorrelations for the estimator, they are not comparable with the autocorrelations for the component. Computing the autocorrelations of the estimator \(i_{t}\) defined by (4.8) in function of the innovations of the process defined by (3.1) is again more complex. The coefficients for the moving average representation for \(i_{t}\) has already been found in (4.12). To evaluate the variance, we have to take the sum of the squares of these coefficients and multiply it by (\(V_{I}/V)^{2}\), giving 0.016, as indicated by item 23 in Table 5, on the line “VAR”. The autocovariances are computed in worksheet Main, in the range BS24 to DC41. Dividing them with the variance located in cell AZ43, we obtain the autocorrelations displayed in cells DD26 to DD41. They correspond to the contents of SEATS output, item 23 in Table 5, column “Estimator”. The variance in units of V is in cell AZ44.
Like the computation of the autocorrelations between the estimates of the two components,  and \(\hat{\imath }_{t}\), we have tried to compute the contemporary (i.e. without lag) cross-correlation between the estimates of the two components. Similarly with the previous results for the irregular component, we had some difficulties to recover exactly the cross-correlation between the two components 0.279 shown in item 24 in Table 6, column “Estimate”. We have also tried to find the cross-correlation between the estimators \(p_{t}\) and \(i_{t}\) using the coefficients of the moving average representation of the two estimators. The results shown in worksheet Main, cell BT47, coincides with the value 0.274 shown in item 24 in Table 6, column “Estimator”.
and \(\hat{\imath }_{t}\), we have tried to compute the contemporary (i.e. without lag) cross-correlation between the estimates of the two components. Similarly with the previous results for the irregular component, we had some difficulties to recover exactly the cross-correlation between the two components 0.279 shown in item 24 in Table 6, column “Estimate”. We have also tried to find the cross-correlation between the estimators \(p_{t}\) and \(i_{t}\) using the coefficients of the moving average representation of the two estimators. The results shown in worksheet Main, cell BT47, coincides with the value 0.274 shown in item 24 in Table 6, column “Estimator”.
4.6 Revisions
This is related to the fact that occurrence of new observations will have a direct impact on the forecasts, and thus on the estimates near the end of the series and, hence, to the computation of one-sided filters, also called concurrent filters. This problem is the subject of several papers (Maravall 1986; Gómez and Maravall 2001b; Bell and Martin 2002). There is no impact on the derivation of the estimates of the component, but on the interpretation side.
Again, let \(P_{t}\) be the permanent component and \(p_{t}\) its estimator, both at time t. The unobservable difference \(f_{t}=P_{t}-p_{t}\) is called the final estimation error. Let \(p_{t|T}\) be the estimator of \(P_{t}\) based on the series sup to time T. When \(t=T\), we obtain what is called the concurrent estimator \(p_{T|T}\). The difference \(t_{T}=P_{T}-p_{T|T}\) is called the total estimation error and can be decomposed, following Pierce (1980), into a sum of two uncorrelated differences:
where the last term \(r_{T}=p_{T}-p_{T|T}\) is called the revision error. We will treat these errors \(t_{t}, f_{t}\) and \(r_{t}\) as stochastic processes and analyze their properties, in particular their variances and their autocorrelation functions.
Let us start with the final estimation error \(f_{t}\). Assuming again that the signal (here the permanent component) and the noise (here the irregular component) do not have common roots in the generalized autoregressive operators, \(\varphi _{P}(B)\) and \(\varphi _{I}(B)\), using notations similar to those at the end of Sect. 2, Pierce (1979) has shown that \(f_{t}\) follows the following stochastic process,
where the white noise process \(a_{t}\) has variance \(V_{P}V_{I}/V\). Here \(\varphi (B)=\varphi _{P}(B)=\nabla , \theta (B)=(1+\theta B), \theta _{P}(B)=(1+B)\) and \(\theta _{I}(B)= \varphi _{I}(B)=1\), this becomes, after simplification by \(\nabla , (1+\theta B)f_{t}=(1+B)a_{t}\). This is similar to the process defined in (4.3) for deriving the Wiener-Kolmogorov weights except that the innovation variance is different. Hence, the autocovariances of the final estimator are proportional to the weights of the Wiener-Kolmogorov filter for the permanent component. The computation of the variance and the autocorrelations is done in the range AE1 to AE37 of worksheet Main. In particular, using (4.4), the variance is \(2V_{P}V_{I}/V(1+ \theta )\). For the series TICD, this is equal to \(V_{f}=0.01095\), as shown in cell AF36. Expressed in units of the variance of the innovations of the process for TICD, this is 0.04696, as shown in item 27 of Table 7, column “Final estimation error”, line VAR. The autocorrelations can be seen in the previous lines. For lags 1 and 12, they are 0.2503 and \(-\)0.0001, respectively.
The revision to the concurrent estimator \(r_{t}=(p_{t}-p_{t|t})\) can be obtained as follows. We have given the expression for the estimator \(p_{t}\) in (2.7). Then \(p_{t|t+m}\) can be obtained by replacing in (2.7) observations \(y_{t+j}\), for \(j>m\), by forecasts made at time \(t+m\) with horizon \(j-m\). Alternatively, we can use (4.10) by taking only terms with powers \(B^{-j}\) for \(j>m.\) Hence, using (4.11), we can write for \(m>0\)
and this is a stationary process, and even a first-order autoregressive process written in reverse time with an autoregressive polynomial \((1-\theta B^{-1})\) and with an innovation process of variance equal to \(V(V_{P}/V)^{2}(1-\theta )^{4}/(1+ \theta )^{2}\theta ^{2m}\). Taking \(m = 0\), the variance of the revision to the concurrent estimator is therefore equal to \(V(V_{P}/V)^{2}(1-\theta )^{4}/\{(1+ \theta )^{2}(1- \theta ^{2})\}=V(V_{P}/V)^{2}(1- \theta )^{3}/(1+\theta )^{3}\). The computations are done in worksheet Main, in the range AI1 to AJ37. The numerical value of the variance is \(V_{r}=0.00274\), see cell AJ36 and, expressed in units of V, it corresponds to the number 0.01175 displayed in item 27 in Table 7, column “Revision in concurrent estimator”, line VAR and also on the line 0 of item 29 in Table 7. Note that the square root of that variance is 0.0523 in cell AK36 and will be used below. The autocorrelations of the revisions can be seen in the previous lines of item 27 in Table 7 and show the exponential decrease and alternating signs typical of an AR(1) process with a negative first-order partial autocorrelation. In particular, autocorrelations for lags 1 and 12 are \(-\)0.4995 and 0.0002, respectively.
The total estimation error of the concurrent estimator \(t_{t}\) defined by (4.13) is the sum of the final estimation error \(f_{t}\) and of the revision error \(r_{t}\), which are uncorrelated. Hence, the covariance at lag j of \(t_{t}\) is the sum of the covariance at lag j of \(f_{t}\) and of the covariance at lag j of \(r_{t}\). Thus the variance of \(t_{t}\) is the sum of the variances of \(f_{t}\) and of \(r_{t}\): \(V_{t}=V_{f}+V_{r}\). It is computed in cell AN36 of worksheet Main and is equal to \(V_{t}=0.01369\) or 0.05871 in units of V. The correlations are deduced in the range from AN1 to AN37 as weighted averages of the autocorrelations of the final estimation errors and the revisions with the respective variances as weights. This corresponds to the contents of item 28 in Table 7. For example, the first-order autocorrelation equals 0.1002 and the autocorrelation for lag 12 is 0 with 4 decimals.
For item 29 in Table 7 and additional periods, we need to use \(m>0\) in (4.14). Additional period 12 corresponds to \(m=12\). The computations are done in worksheet Main in the range AQ1 to AV36. The number shown 0.683E-09 can be seen in cell AU18. For item 31 in Table 8, the column entitled “Trend-Cycle standard error of revision” can be seen in the range AV6 to AV30 of the worksheet, going from bottom to top and with some approximations for long periods. For period 0, the number 0.05235 which can be seen in cell AV6 is the square root of the variance of revision error \(V_{r}=0.00274\) in cell AT6 already mentioned in cell AJ36. The percentage reduction in the standard error after one year, 99.98 %, shown in item 30 of Table 7, is obtained in cell AW6. Computation of the standard errors of the total error, obtained by adding \(V_{f}=0.01095\) to the variance of the revision error, can be seen in cells BS63 to CA71.
There remains to derive several columns of item 32 in Table 8 which were not considered in Sect. 4.1. They are about the standard errors of the preliminary estimator of the permanent component total and revision errors. Here we analyze for \(m>0\):
Again, the variance of the first term is \(V_{f}=0.01095\). The variance of the second term depends on m since, according to (4.10)
Hence the variances are given by \(V\{\xi _{0}^{2}+\xi _{{-1}}^{2} (m-1)+\xi _{1}^{2}/(1-\theta ^{2})\}\), equal respectively for \(m=1\), 2, 3, to 0.2076, 0.7320, 1.2563, and taking square roots, this corresponds to the respective standard deviations 0.4557, 0.8556, 1.121, in agreement with item 32 in Table 8. Adding these variances to \(V_{f}=0.01095\) provides the variances of the total errors 0.2186, 0.7429, 1.2672 with square roots 0.4675, 0.8619, 1.126, again for \(m=1\), 2, 3, and in agreement with SEATS output. The computation of the weights of the component estimator is shown in worksheet Main, in the range BS73 to BX77.
4.7 Growth rates
First of all, as already indicated in Sect. 3.7, the fifth part of the SEATS output, entitled “Rates of growth”, provides growths since the model is applied on the data, not on their logarithms. Hence we compute differences and standard errors are based on linear ARIMA models. In the presence of a log-transform, effective rates would be computed and standard error would be based on a linearized version of ARIMA models. Since the tables are numbered, we will use these table numbers in addition to the item indication.
SEATS Table 5.1 (item 35 in Table 9) shows the period-to-period growth estimation error variance for the concurrent estimator, so the first differences of the final estimation error, the revision error and the total estimation error. For example, the final estimation error, denoted \(f_{t}\), has been analysed in Sect. 4.6. We need to compute \(\hbox {var}(\nabla f_{t})\) which is equal to \(\hbox {var}(f_{t})+\hbox {var}(f_{t-1})-2\hbox {cov}(f_{t}, f_{t-1}) =2\times 0.01095\times (1-0.2503) = 0.016\), see cell AF40.
SEATS Table 5.2 (item 36 in Table 10) shows the period-to-period growth for the most recent periods for the original series and the trend (with standard error of revision for the latter). The second column “Original series” coincides with the differenced series also shown in item 3 of Table 1, see also range BJ54 to BJ113 of worksheet Main, except that the rows are displayed in reverse order. The third column entitled “Trend-Cycle Estimate” contains \(\nabla P_{t}\), already shown in range AE54 to AE113, also in reverse order.
SEATS Table 5.3 (item 37 in Table 10) shows accumulated growth during the present year, thus at the last date T or Dec-1979. For the original series, this is the seasonal difference \(\nabla _{12}y_{T}=y_{T}-y_{T-12}\), whereas for the trend-cycle, this is the seasonal difference \(\nabla _{12}P_{T}=P_{T}-P_{T-12}\). These differences are computed in cells BN113 and BO113 of worksheet Main. The Trend-Cycle SER = 0.523E\(-\)1 which is displayed is the standard error of revision for the trend shown in cell AV6 or AK36 and discussed in Sect. 4.6.
SEATS Table 5.4 (item 38 in Table 10) shows the annual growth estimation error variance for the concurrent estimator, which is a first seasonal difference of the final estimation error, the sum of the revision error and the total estimation error. As indicated, the numbers are to be multiplied by 10. For example, the first one, denoted \(f_{t}\), has been analysed in Sect. 4.6. We need to compute \(\hbox {var}(\nabla _{12}f_{t})\) which is equal to \(\hbox {var}(f_{t})+\hbox {var}(f_{t-12})-2\hbox {cov}(f_{t}, f_{t-12})= 2\times 0.01095\times (1+0.0001) = 0.0219\), see cell AF41.
SEATS Table 5.5 (item 39 in Table 11) shows the annual growth for the most recent periods, thus not only at the last date T or Dec-1979, as in SEATS Table 5.3, for the original series and the trend-cycle (with standard error of revision for the latter). For the original series, this is the seasonal difference \(\nabla _{12}y_{t}=y_{t}-y_{t-12}\), whereas for the trend-cycle, this is the seasonal difference \(\nabla _{12}P_{t}=P_{t}-P_{t-12}\). Hence the row for Dec-1979 corresponds to SEATS Table 5.3. The other elements are computed in ranges BN65 to BN113 and BO65 to BO113 of worksheet Main but in reverse order. The standard error of revisions are those in cells AV6 to AV30, already discussed in Sect. 4.6.
SEATS Table 5.6 (item 40 in Table 11) shows annual centred growth rates, which are according to the documentation, base of a 6-month forecast and the corresponding value 12 months before. Hence, the difference between the forecast in Jun-1980 and the value in Jun-1979. For the original series, it is \(13.28 - 10.44 = 3.30\) on row Dec-1979. On row Nov-1979, we have the difference between the forecast for May-1980 and the value for May-1979. The standard errors are the square roots of \(V(1+5(1+\theta )^{2})\) and \(V(1+4(1+\theta )^{2})\), respectively, since the horizons are 6 and 5, respectively, using the standard errors for future values presented in Sect. 4.1.
SEATS Table 5.7 (item 41 in Table 11) shows the growth forecasts for the original series and the trend-cycle, with standard error of revision. More precisely, the first row of the table refers to forecasts one period ahead and the second row to 12 periods ahead, both at time T. In our case, the forecasts are all equal to 13.277, so the difference with the observation at time T of the original series, 13.42, is \(-\)0.143. The difference with the value at time T of the trend-cycle, 13.438, is \(-\)0.161. These two numbers can be found on the first two rows. The standard errors are different in the two cases. For one-period-ahead forecasts it corresponds to the square root of V for the original series, hence 0.483 for the original series. For the trend-cycle, using the expression for \(p_{t+m|t}\) and subtracting from (4.10) yields:
hence, the standard error is 0.276, as can be seen in cell BQ124. For 12-periods-ahead forecasts and the original series, the SER can be computed in a standard way from the pure MA form of the respective model. For the original series of an ARIMA(0,1,1) process with MA coefficient \(\theta \) and with innovation variance V, it is the square root of \(V(1+11(1+\theta )^{2})\), hence 2.449.
5 Conclusions
SEATS is now essential for seasonal adjustment since it is used in both Bureau of the Census X-13ARIMA-SEATS and Bank of Spain TRAMO-SEATS, the main two software packages for seasonal adjustment. There is a large amount of literature on SEATS but, with a few exceptions, it is not intended for the final user.
Our purpose was to explain the text output of SEATS on a simple example. The example is based on a non-seasonal series of U.S. interest rates on certificates of deposit. The model-based decomposition in two components is simple and does not involve a seasonal model. Thanks to that, it is possible to check the computations rather easily using Microsoft Excel. In particular, we have verified the different admissible decompositions; the selection of the canonical decomposition using the criterion of a minimal variance for the irregular component and using a pseudo-spectrum criterion; the derivation of the Wiener-Kolmogorov filter for the two components; and the difference between theoretical components, their estimators and their estimates. We could obtain the latter estimates but with a limited accuracy for the irregular component. We have also checked the autocorrelations of the estimates, with only two significant digits for some correlations involving the irregular component. On the contrary all the results relative to the estimators could be confirmed.
We were able to obtain most parts of the output. Note that we did not try to check the graphical output. This can be the subject of another paper. We have only found a real repeated mistake (items 16 in Table 3, 23 in Table 5, 28 and 30 in Table 7) in the text output, concerning the variance of the innovations of the series and a small mistake (item 17 in Table 4) which will be corrected with build 935. We have also pointed out some discordances (in certain standard errors for rates of growth not mentioned above) and a few misprints directly to the author. This does not affect the effective impact of SEATS which is a solid piece of software for seasonal adjustment.
One objection against the present paper is that the model is much too simple and without any seasonal component. A referee has made the following suggestion: to use a specific ARIMA model that should be as simple as possible, but should contain a seasonal component. For that purpose a pure seasonal model like \((0,0,0)(0,1,1)_{s}\), with \(s=2\) may be considered, as it admits three components (cycle-trend, seasonal component and irregular component) but it requires the estimation of few parameters and few lags because \(s=2\). Of course another series instead of interest rates should be used, probably an artificial time series or a half-yearly version of a long real series. This would be a different paper, however, and can be the subject of a follow-up paper, possibly in collaboration. Also it is unclear whether Excel would be enough for the task.
Notes
The trend-cycle can be further decomposed into trend and cycle using ARIMA models that reproduce the Hodrick-Prescott filter, with some improvements, see Kaiser and Maravall (2005).
When \(s=12\), a transitory component is needed in some cases: (i) if \(p+d+12(P+D)<q+12Q\); (ii) if the case of an AR(1) polynomial \((1+\phi \hbox {B})\) with a coefficient \(\phi >-0.2\); (iii) series with peaks in the spectrum which are not associated to frequency 0 nor with the seasonal frequencies.
We assume \(q\le 4\), because otherwise \(I_{t}\) would be a moving average of order \(q-4\), not a white noise.
The computations in SEATS are not precisely performed that way. The filter to estimate the component is derived in the frequency domain and does not explicitly require the models of the components. Given that the average user looks better in the time domain, we have preferred that equivalent approach.
Their treatment is based on a random walk signal, whereas an ARIMA(0,1,1) process is used here.
This is to save space and to concentrate on items that are commented on. For example, the partial autocorrelations are never shown. An unedited output is available (Online Resource 4).
No outlier was detected so the corrected series is identical to the original series.
Note a small mistake here and in some other places (in items 23, 28, 30) in builds up to 934 of the program, since the innovation standard deviation 0.4829 is printed instead of the innovation variance 0.2332. The mistake will be corrected in build 935 which was not publicly available at the time of writing.
It is based on the file CH13EX06.xls on the CD-Rom of Mélard (2007) except that there a model with a constant was used, see \(\hbox {footnote}^{1}\). A document (Online Resource 3) providing some instructions is also given but these instructions do not reflect the slight changes due to the absence of the constant; makes use of the Box-Jenkins parameterization for AR and MA coefficients; and comments a former version of SEATS. It covers also some other aspects, such as generating artificial series from the models for the trend-cycle and the irregular and showing that the autocorrelations of their sum behave like the series TICD.
Note that the sum of the two component series differs from the original series by 0.000004 on average, see cell BG116, showing only 5 correct significant digits. When the MA(1) parameter estimate 0.4995 is used, thus with four decimal places, the forecasts and backcasts are not very accurate, and the difference becomes 0.0002 on average, showing only 2 to 3 correct significant digits. To avoid numerical instability, Pollock (2006) recommends to compute the irregular component using the filter and to deduce the permanent component.
Based on Mélard (2006).
References
Bell W (1984) Signal extraction for nonstationary time series. Ann Stat 12:646–664
Bell W, Martin DEK (2002) Computation of asymmetric signal extraction filters and mean squared error for ARIMA component models. J Time Ser Anal 25:603–623
Box GEP, Jenkins GM, Reinsel GC (2008) Time series analysis, forecasting and control, 4th edn. Wiley, New York
Burman JP (1980) Seasonal adjustment by signal extraction. J R Stat Soc Ser A 143:321–337
Cleveland WP, Tiao GC (1976) Decomposition of seasonal time series: a model for the X-11 program. J Am Stat Assoc 71:581–587
Cohen A, Lotfi S, Mélard G, Ouakasse A, Wouters A (2002) Self-training in time series analysis. Hawaii Int Conf Stat. http://homepages.ulb.ac.be/~gmelard/Hawaii02.pdf
Dagum EB (1980) The X-11-ARIMA seasonal adjustment method. Statistics Canada, Catalogue No. 12-564E. https://www.census.gov/ts/papers/1980X11ARIMAManual.pdf
Demeure J, Mullis T (1989) The Euclid algorithm and the fast computation of cross-covariance and autocovariance sequences. IEEE Trans Acoust Speech Signal Process 37:545–552
Findley DF, Monsell BC, Bell WR, Otto MC, Chen BC (1998) New capabilities and methods of the X-12-ARIMA seasonal adjustment program. J Bus Econ Stat 16:127–152
Fiorentini G, Planas C (2001) Overcoming nonadmissibility in ARIMA-model-based signal extraction. J Bus Econ Stat 19:455–464
Gómez V (1999) Three equivalent methods for filtering finite nonstationary time series. J Bus Econ Stat 17:109–116
Gómez V, Maravall A (1994) Estimation, prediction, and interpolation for nonstationary series with the Kalman filter. J Am Stat Assoc 89:611–624
Gómez V, Maravall A (2001a) Automatic modeling methods for univariate series. In: Peña D, Tiao GC, Tsay RS (eds) A course in time series analysis. Wiley, New York, pp 171–201
Gómez V, Maravall A (2001b) Seasonal adjustment and signal extraction in economic time series. In: Peña D, Tiao GC, Tsay RS (eds) A course in time series analysis. Wiley, New York, pp 202–246
Hatanaka M, Suzuki M (1967) A theory of the pseudospectrum and its application to nonstationary dynamic econometric models. In: Shubik M (ed) Essays in mathematical economics in honour of Oskar Morgenstern. Princeton University Press, Princeton, pp 443–466
Hillmer SC, Tiao GC (1982) An ARIMA-model-based approach to seasonal adjustment. J Am Stat Assoc 77:63–70
Kaiser R, Maravall A (2001) Notes on time series analysis, ARIMA models and signal extraction. Working Paper 0012, Bank of Spain
Kaiser R, Maravall A (2005) Combining filter design with model-based filtering (with an application to business-cycle estimation). Int J Forecast 21:691–710
Ladiray D, Quenneville B (2002) Seasonal adjustment with the X-11 method. Springer-Verlag, New York
Maravall A (1986) Revisions in ARIMA signal processing. J Am Stat Assoc 81:736–740
Maravall A (1994) Use and misuse of unobserved components in economic forecasting. J Forecast 13:157–178
Maravall A (2003) A class of diagnostics in the ARIMA-model-based decomposition of a time series. Working paper, Bank of Spain
Maravall A, Planas C (1999) Estimation error and the specification of unobserved component models. J Econom 92:325–353
McElroy T (2008) Matrix formulas for nonstationary ARIMA signal extraction. Econom Theory 24:988–1009
McLeod AI (1975) Derivation of the theoretical autocovariance function of autoregressive-moving average time series. J R Stat Soc Ser C Appl Stat 24:255–256
Mélard, G (2006) Initiation à l’analyse des séries temporelles et à la prévision. Modulad 35. http://www-rocq.inria.fr/axis/modulad/numero-35/Tutoriel-melard-35/35_res_melard.htm
Mélard G (2007) Méthodes de prévision à court terme, 2nd edition (with CD-Rom). Editions de l’Université de Bruxelles, Bruxelles and Editions Ellipses, Paris
Mélard G (2014) On the accuracy of statistical procedures in Microsoft Excel 2010. Comput Stat 29:1095–1125
Pierce DA (1979) Signal extraction error in nonstationary time series. Ann Stat 7:1303–1320
Pierce DA (1980) Data revisions with moving average seasonal adjustment procedures. J Econom 14:95–114
Pollock DSG (2002) A review of TSW: the Windows version of the TRAMO-SEATS program. J Appl Econ 17:291–299
Pollock DSG (2006) Econometric methods of signal extraction. Comput Stat Data Anal 50:2268–2292
Priestley MB (1981) Spectral analysis and time series. Volume 1: Univariate series. Academic Press, London
Shiskin J, Eisenpress H (1957) Seasonal adjustment by electronic computer methods. J Am Stat Assoc 52:415–449
Time Series Research Staff (2013) X-13ARIMA-SEATS Reference Manual. U.S. Census Bureau, Statistical Research Division, Washington, DC 20233
Tunnicliffe Wilson G (1979) Some efficient computational procedures for high order ARMA models. J Stat Comput Simul 8:303–309
Whittle P (1983) Prediction and regulation by linear least-square method, 2nd edn. University of Minnessota Press, Minneapolis
Acknowledgments
This project was started when I was involved in the development of a self-learning course for the National Bank of Belgium, see Cohen et al. (2002). The material included descriptions of the Census X-11 procedure; multiple regression; ARIMA models and chapters on X-12-ARIMA and TRAMO-SEATS; and using Microsoft Excel or free packages like Demetra. See the final product on the CD-Rom of Mélard (2007). For the present paper I received the help from several persons, including Stephen Pollock and Brian Monsell. I thank them all. I am particularly grateful to Agustín Maravall and the two referees and the editor Gabriele Fiorentini who made extremely useful suggestions for improving the text, especially suggesting Appendix 2. Agustín Maravall helped also with his course notes, recommendations and numerous comments on previous versions. I thank also Michelle Crowley for her editing contribution. Of course the remaining errors are mine. This paper is offered in the honour of Agustín Maravall. We associate his collaborators to our congratulations for his bright career.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix 1: An introduction to spectral analysis
Besides the temporal approach to time series used in most of this paper, such as autocorrelations, filters and ARIMA modelling, another approach is possible: the frequency or spectral approach. In mathematical terms, it comes from the Fourier transform of the temporal approach. A priori, the information must be similar but there are some applications where the spectral approach is instructive. It occurs in the treatment of seasonality, or those applications where oscillatory phenomena predominate. To fix ideas, assume a stationary process where time is expressed in months. The spectrum or spectral density is the distribution of the scatter, specifically the variance, as a function of the frequency, or its inverse which is the period:Footnote 13
-
low frequencies (corresponding to long periods) are related to the long term, several years;
-
high frequencies (corresponding to short periods) are related to the short term, a few months at most;
-
intermediary frequencies (corresponding to medium periods) are relative to the medium term.
Frequencies are expressed as numbers between 0 and 0.5. The period is the inverse of the frequency and varies between infinity (=1/0) and 2 (=1/0.5). We will denote f the frequency. Some authors express the frequency as an angular frequency, measured in radians. If we denote \(\upomega \) (Greek omega) the angular frequency, it is \(\upomega =2 \uppi f\), where \(\uppi =3.1415...\) The angular frequency varies between 0 and \(\uppi \). The period is then expressed by \(2\uppi /\upomega \) .
Denote S(f) the spectral density, in short the spectrum at frequency f, f in [0; 0.5]. The variance is the “sum” of all S(f), which is written as an integral
More generally, the spectral density is the Fourier transform of the autocovariance function:
which yields (A1.1) in the case where \(k= 0\). Conversely, we can write the inverse Fourier transform:
taking into account that \(\gamma _{k}= \gamma _{-k}\). Note that the series \(R(z)=\sum _{k=-\infty }^{\infty }{\gamma _{k} z^{k}}\) is the autocovariance generating function. It can be obtained by replacing in S(f) the imaginary exponential \(e^{2\pi if}\) by z.
For example, consider an MA(1) process defined by \(y_{t}=e_{t}+\theta e_{t-1}\), where the innovation variance is \(\upsigma ^{2}\). The autocovariance at lag 0 is \((1+\theta ^{2})\upsigma ^{2}\) and the autocovariance at lag +1 and \(-\)1 are equal to \(\theta \upsigma ^{2}\) so that there
If \(\theta <0\), there is a negative autocorrelation at lag 1, and the spectrum is higher at 0.5 than at 0 (see Fig. 4, left).Footnote 14 If \(\theta >0\), there is a positive autocorrelation at lag 1, resulting in a higher spectrum at 0 than at 0.5 (see Fig. 4, right). If \(\theta =0\), the process is white noise and its spectrum is constant, i.e. all frequencies have the same density. An equivalent alternative approach is to define S(f) as the square of the module of the polynomial moving average evaluated at \(e^{2\pi if}\):
In the case of an \(\hbox {AR}(p)\) process, we do the same with the inverse of the autoregressive polynomial, for example for an AR(4) process, defined by the equation
where the innovation variance is 1:
Fig. 5 show cases of an AR(1) process (A1.2) with \(\phi _{1}=\phi ,\phi _{2}=\phi _{3}= \phi _{4}=0\).
For a monthly series, a seasonality in the series will be shown by a large frequency content at frequencies that correspond to period 12 (since 1 year \(=\) 12 months) but also its submultiples 12/2 \(=\) 6, 12/3 \(=\) 4, 12/4 \(=\) 3, 12/5 \(=\) 2.4 and 12/6 \(=\) 2. Consider for example the following process:
It is a stationary process with roots for the autoregressive polynomial in module equal to \((1/0.8)^{1/12}>1\). It is also invertible because the root of the moving average polynomial is \((1/0.6)>1\). The spectrum is defined as the ratio of the squares of the following modules:
The spectrum will feature spikes at frequencies multiple of 1/12. Sometimes spectra are considered on a logarithmic scale. The logarithmic scale is aimed at compressing large values. For the process defined by (A1.4), the spectrum is illustrated on the left of Fig. 6.
So far we have defined the spectral density of a stationary process. The case of a non-stationary process is more complicated. We mean here the case of an ARIMA or SARIMA process having unit roots, because of the presence of a regular difference and/or of a seasonal difference. In these cases, the approach by the autocorrelations no longer holds. Nevertheless, we can still define the generalized spectrum by the second approach (see Hatanaka and Suzuki 1967), given that the spectral density can be infinite for certain frequencies. For example the generalized spectrum of ARIMA(0,1,1) process, defined by the equation \(y_{t}-y_{t-1}=e_{t}+\theta e_{t-1}\), with innovation variance equal to \(\upsigma ^{2}\) is:
Since cos(0) = 1, at frequency 0, the spectrum is proportional to the inverse of 2 \(-\) 2 = 0, so it is infinite. An example is treated at the right of Fig. 6 or in Fig. 2.
To estimate the pseudo-spectrum using a series, several techniques are possible. There are methods using the Fourier transform of the estimated autocorrelations and then smoothing the values obtained in a narrow window around a given frequency. In an associated Excel file (Online Resource 5), we have illustrated the autoregressive approach which consists of adjusting the series by an AR model of high enough order and calculating the spectrum of the corresponding process, without the restrictions on series length of the fast Fourier transform.
Appendix 2: Introduction to the use of spectral analysis in SEATS
In the main text of the paper, especially in Sects. 3.2, 3.3 and 3.4, we have presented a conceptual approach behind SEATS which is not the procedure effectively used. For computational convenience, SEATS follows an alternative approach based on spectral analysis, as in Burman (1980). More precisely, the (generalized) spectral density of the series is first derived from the ARIMA model obtained using TRAMO on the (generally corrected) time series.
For the three-component model (2.1), since the components are assumed to be mutually independent, the spectrum of the series is the sum of the spectra of the three components:
In Appendix 1, we have noticed the basic features of trend (and cycle), seasonal and irregular components: the trend-cycle or permanent component corresponds to large values close to \(f=0\) (e.g. in Fig. 5, left part or in Fig. 6, right part). The seasonal component corresponds to large values close to \(f=0.5(j/6), j=1, 2, 3, 4, 5, 6\) (e.g. in Fig. 6, left and right parts). The irregular component corresponds to a flat or even constant spectrum (e.g. in Fig. 4, both parts). The models for the components in SEATS are in fact obtained as in Burman (1980), by first decomposing the spectrum of the series by means of a partial fraction expansion in terms of the variable \(\hbox {cos}(2 \pi if)=(e^{-2\pi if}+e^{2\pi if})/2\). Then, the decomposition is made canonical in a second step to identify the components and the components spectra are correspondingly changed. It is to be noticed that the link between the autocovariance generating function of the series and the spectrum is exploited, see Appendix 1. Consequently, the spectra for the components give the models for the theoretical components through their covariance generating functions. In addition, the Wiener-Kolmogorov filter for the \(P_{t}\) component is
where \(R_{P}\) and \(R_{y}\) are the autocovariance generating functions of the components \(P_{t}\) and the series \(y_{t}\). Finally, the expression for  gives the model for the historical estimator
gives the model for the historical estimator  after we have replaced \(y_{t}\) with \([\theta (B)\varphi (B)]e_{t}\) in the previous expression. This model depends on both B and \(B^{-1}\) and assumes that the doubly infinite series is known. The weights \(\nu _{j}\) given by \(\upsilon ^{P}(B,B^{-1})\) are in fact the autocovariances of the auxiliary process mentioned in (2.8).
after we have replaced \(y_{t}\) with \([\theta (B)\varphi (B)]e_{t}\) in the previous expression. This model depends on both B and \(B^{-1}\) and assumes that the doubly infinite series is known. The weights \(\nu _{j}\) given by \(\upsilon ^{P}(B,B^{-1})\) are in fact the autocovariances of the auxiliary process mentioned in (2.8).
In the case of the ARIMA(0,1,1) model for the interest rates of U.S. certificates of deposit, the spectrum is given by (A1.5) but S(f) can also be written as a function R of \(e^{2\pi if}\)
or, replacing \(e^{2\pi if}\) by z, and denoting like in the text the innovation variance \(\sigma ^{2}\) by V, as a rational function of z which is a generalized autocovariance generating function:
Now we can introduce the auxiliary variable \(x=(z+z^{-1})\) and obtain a partial fraction expansion
The first term corresponds to the irregular component and the second term, to the trend component. Moreover we obtain directly, like in Sect. 2, the two variances \(V_{I}\) and \(V_{P}\) by equating the expressions for the numerators: \(V_{I}=- \theta V\) and \(V_{P}= (1+\theta ^{2})V\), giving a non-admissible decomposition. But we can add and subtract a constant K, for example, to the right hand side of (A2.3) to get
This leads to (3.4). The canonical decomposition is obtained by taking the maximum K as long as meaningful models for \(P_{t}\) and \(I_{t}\) are obtained.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mélard, G. On some remarks about SEATS signal extraction. SERIEs 7, 53–98 (2016). https://doi.org/10.1007/s13209-015-0137-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-015-0137-y