Introduction

The gaseous bubbles in a liquid have been used in broad such as the controlling of protein conformations (Liu et al. 2005; Zhou et al. 2004; Zhang et al. 2013; Okumura and Itoh 2014), the drug delivery studies (Lukianova-Hleb et al. 2012; Li et al. 2015; Hernandez et al. 2017), the direct transfer of large-size graphene films with decreased defects (Gao et al. 2014; Guo et al. 2018), and the performance of chemical mechanical polishing (Tsai et al. 2007; Zhang et al. 2016a, b, 2018). For example, a sudden formation of nitrogen nanobubbles might induce the unfolding of protein in our body and has been associated with the origin of ‘Diver’s disease’ (Zhang et al. 2013). Even though there have been growing interests in the application of the nanobubbles, a fundamental understanding on a formation mechanism is still deficient, especially due to the limit of proper characterizing tools.

Growth dynamics of large nanobubble, whose lateral size is over 100 nm, have been studied with the optical microscopy. Chan et al. used total internal reflection fluorescence microscopy to measure the growth of the height of pinned nanobubble which is initiated by the coalescence of the two nanobubbles (Chan et al. 2015). The atomic force microscopic study also obtained the successive height profiles of growing nanobubble and resolved the existence of the circular wetting layer which initiates the growth of nanobubble (Fang et al. 2016). These nanobubbles can be stabilized by the surface pinning of three phase contact line (Liu and Zhang 2013, 2014; Tan et al. 2017; Weijs and Lohse 2013; Lohse and Zhang 2015a, b). However, there are few studies on the growth dynamics of nanobubble at 10 nm scale, at which the conventional atomic force microscopy and optical microscopy are hard to achieve (Chen et al. 2015; Huang et al. 2013).

In this article, we succeeded to characterize the initial growth dynamics of small nanobubbles encapsulated between the graphene liquid cell (GLC) using the high-resolution transmission electron microscopy (HRTEM). The observed temporal growth of 10 nm nanobubble is well described by the diffusion theory in gas–liquid system considering the size of GLC. Interestingly, we found that the required amount of gas in the growth of nanobubbles is strongly dependent on the size of the GLC system, which determines the oversaturation condition. As the size of the system decreases, more amount of gas is required to oversaturate the system, which initiate the formation of nanobubbles.

Results

To image the temporal growth of the nanobubble at nm-scale resolution, we prepared the graphene liquid cell (GLC) (Shin et al. 2015; Park et al. 2015a, b; Algara-Siller et al. 2015; Yuk et al. 2012, 2014; Chen et al. 2013; Wang et al. 2014; De Clercq et al. 2014) fabricated on a TEM grid. Two adjacent graphene layers were stacked via strong van der Waals force, efficiently preventing water from leaking out to the ultrahigh vacuum environment in TEM chamber. Atomic thickness of graphene is also critical to achieve high-resolution image in liquid phase due to the minimized scattered electron from the graphene. The size of water-encapsulated graphene pocket in GLC was determined as 100 nm height and 1 µm diameter (Supplementary Fig. S1). Note that we intentionally add Pt nanoparticles because observing the diffusion of Pt nanoparticle is efficient to recognize the region where confined water exists in GLC (Methods for the detailed procedure of preparation of GLC and Pt nanoparticles).

Nanobubbles are generated by radiolysis process, which occurs simultaneously during TEM measurement. The emitted electrons from electron gun interact with the water molecules and decomposes them into the primary species including H2 molecules (Caer 2011). The concentration of H2 saturates immediately (~ 1 ms) and prepared for the formation of the nanobubbles (Schneider et al. 2014).

From the TEM observation of the nanobubble growth, we measured the temporal change of the radius of nanobubbles during 2 min. We take the snapshots of the system during formation and growth of five hydrogen gas nanobubbles (Bubble 1–5) with temporal resolution of 1 s and Fig. 1b shows four of them (Supplementary Movie S1 for the full movie). The formation of nanobubbles is completed until t = 40 s and they grow steady by absorbing the surrounding gas molecules (t = 100 s and 120 s). Because nanobubble 2 starts to exit the TEM observation window at t > 70 s, we collect its radius data until t = 70 s. As shown in snapshots in Fig. 1b, small fraction of nanobubble 2 is still observed, but estimated radius has large uncertainty and we do not use it. Note that we do not observe any coalescence event between two adjacent nanobubbles within our limited observation time of 120 s, but such nanobubble merging may be unlikely due to the inter-bubble liquid that mediates the gas influx and controls the nanobubble growth, as discussed by the atomic force microscopy experiment (Lhuissier et al. 2014).

Fig. 1
figure 1

Growth of nanobubble in the GLC observed via TEM. a Schematic of nanobubble formed by the aggregation (yellow arrows) of hydrogen gas molecules that are produced during the electron beam-induced radiolysis reaction of the water (red arrows). b Four snapshots of TEM images showing formation and growth of five nanobubbles in the liquid water-encapsulated by GLC (Supplementary Movie S1). Nanobubbles are numbered from 1 to 5. The snapshot at t = 40 s has relatively poor contrast, so the dotted circle surrounding nanobubble is drawn for the visual guidance. c Temporal evolution of the radius of the five nanobubbles measured during in situ TEM observation. Arrow represents the first appearance time of the corresponding nanobubble, which occurs randomly depending on the local conditions of fluctuations and gas densities. Due to the lack of the data, the data of nanobubble 1 between t = 60 and 65 s are not presented. Additionally, the data of nanobubble 2 are collected until t = 70 s because nanobubble 2 starts to exit the TEM observation window at t > 70 s and estimated radius has large uncertainty

Full size image

Figure 1c is plot of radius of the observed nanobubbles. The radius of first appeared nanobubbles are all similar and about 5–10 nm (denoted as arrows). This value is similar with the previous result ~ 5 nm obtained from the electrochemical measurement of the hydrogen nanobubble nuclei on the Pt nanoelectrode (German et al. 2018). It implies that the first appearance of the nanobubble on the TEM window is related with the nucleation event. Once the nanobubble is formed, the subsequent growth curve denotes that the nanobubble grows continuously, which shows that diffusion of the gas monomer mainly attributes to the nanobubble growth.

Discussion

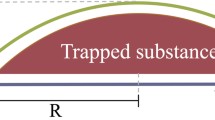
We use the classical diffusion theory to describe the growth dynamics. We consider the single spherical-cap-shaped nanobubble of projected radius Rb attached on the surface (Fig. 2a). This single nanobubble is confined in the finite cell with the height H and the lateral length L. By applying the periodic boundary condition in lateral dimensions, we can understand the behavior of the group of nanobubbles in the experiment (Fig. 1b) from single nanobubble model. Here H and L can be understood as the heights of the GLC and the average distance between the center of the adjacent nanobubbles. Note that height difference in the center of the few µm GLC used in experiment is only few nm along the 100 nm of lateral dimension, which justifies the simplified rectangular box we used in the numerical model. Also note that our model considers the finite size of the system, different with the conventional growth model which assumes infinite system (Epstein and Plesset 1950).

Fig. 2
figure 2

Numerical model of nanobubble. a Schematic of the nanobubble system confined within the rectangular box, characterize by the horizontal and vertical length of L and H, respectively. Note that the periodic boundary condition is used along the horizontal direction. b Temporal evolution of the radius of the nanobubble obtained from Eq. (5) (lines). Initial concentration \({c_i}\) is rescaled by the oversaturation \(\zeta\). For comparison, experimental data from Fig. 1c is used (dot) with the new time variable \({t_o}\). \({t_o}\) = 0 denotes the moment when the nanobubble is first appeared on the imaging window. The data of Bubble 5 is omitted because we cannot specify its moment of appearance from the observation

Full size image

In the diffusion theory, the gas flux between two regions is determined by the concentration difference between them. The diffusive volume outflux from a nanobubble can be expressed as (Brenner and Lohse 2008)

$$\frac{{{\text{d}}{V_{\text{b}}}}}{{{\text{d}}t}}=\pi {R_{\text{b}}}D\left( {\frac{{{c_{\text{l}}}}}{{{c_{\text{s}}}}} - 1} \right),$$
(1)

where \(D\) is the diffusion coefficient of the gas in the liquid, \({R_{\text{b}}}\) is the projected radius of the nanobubble, \({c_{\text{s}}}\) is the concentration of gas just outside of the nanobubble and \({c_{\text{l}}}\) is the gas concentration far from the nanobubble.

Here, \({c_{\text{s}}}\) can be obtained by the Henry’s law,

$${c_{\text{s}}}=\frac{{{p_{\text{b}}}}}{{{k_{\text{H}}}}}=\frac{1}{{{k_{\text{H}}}}}\left( {{P_0}+\frac{{2\sigma \sin \theta }}{{{R_{\text{b}}}}}} \right),$$
(2)

where \({k_{\text{H}}}\) is the Henry’s law constant, \(\sigma\) is the surface tension of water (0.072 N/m) and \(\theta\) is the contact angle between bubble and substrate. The parameter \({c_{\text{l}}}\) can be expressed as

$${c_{\text{l}}}=\frac{{{N_{\text{g}}} - {N_{{\text{g}},{\text{b}}}}}}{{{N_{\text{l}}}}},$$
(3)

where \({N_{\text{l}}}\), \({N_{\text{g}}}\) is the number of liquid and gas molecule, and \({N_{{\text{g}},{\text{b}}}}\) is the number of gas molecules in the bubble. If there is no bubble, \({c_{\text{l}}}\) increases to \({N_{\text{g}}}/{N_{\text{l}}}\). With the ideal gas law, \({N_{{\text{g}},{\text{b}}}}\) can be evaluated as

$${N_{{\text{g}},{\text{b}}}}=\frac{{{p_{\text{b}}}{V_{\text{b}}}}}{{{k_{\text{B}}}T}},$$
(4)

where \({p_{\text{b}}}\) is the Laplace pressure and \({V_{\text{b}}}=V\left( \theta \right){R^3}\) where \(V\left( \theta \right)=\pi \left( {2 - 3\cos \theta +{\text{co}}{{\text{s}}^3}\theta } \right)/3{\text{si}}{{\text{n}}^3}\theta\).

By combining Eqs. (1) to (4), we can obtain the differential equation of the time derivative of \({R_{\text{b}}}\),

$$\frac{{{\text{d}}{R_{\text{b}}}}}{{{\text{d}}t}}=\frac{{\pi D}}{{3V\left( \theta \right)}}\frac{1}{{{R_{\text{b}}}}}\left[ {\frac{{{k_{\text{H}}}}}{{{N_{\text{l}}}}}\frac{{{N_{\text{g}}} - \frac{{V\left( \theta \right)}}{{{k_{\text{B}}}T}}R_{{\text{b}}}^{3}\left( {{P_0}+\frac{{2\sigma \sin \theta }}{{{R_{\text{b}}}}}} \right)}}{{{P_0}+\frac{{2\sigma \sin \theta }}{{{R_{\text{b}}}}}}} - 1} \right]$$
(5)

which can be solved by the standard Runge–Kutta method.

Even the growth dynamics of nanobubble [Eq. (5)] is complex, Eq. (1) exhibits that the condition for the nanobubble growth is simple. Nanobubble can grow when gas concentration in liquid exceeds that on bubble interface, which is the definition of the gas oversaturation. We define gas oversaturation \(\zeta\) from Eq. (1) as

$$\zeta =\frac{{{c_{\text{l}}}}}{{{c_{\text{s}}}}} - 1$$
(6)

and nanobubble grows when \(\zeta\) > 0 and dissolves when \(\zeta\) < 0. When the nanobubble is not confined within the GLC but is in the bulk liquid, Eq. (8) reduces to the conventional definition of the gas oversaturation at infinite system \({\zeta _\infty }\) as (Lohse and Zhang 2015b)

$${\zeta _\infty }{\text{~}}=\frac{{{c_{\text{i}}}}}{{{c_{\text{s}}}}} - 1$$
(7)

where \({c_{\text{i}}}={N_{\text{g}}}/{N_{\text{l}}}\).

To compare Eq. (5) with the experimental results, we start with the initial radius of nanobubble \({R_{\text{b}}}\left( {{t_o}=0} \right)\) = 9 nm. \({t_o}=0\) means the moment that formation of nanobubble is first observed. We use \({t_o}=0\), not the lab time \(t\) because the first observation times of nanobubbles in the experiment are all different (arrows in Fig. 1c). We solve Eq. (5) with parameters L = 100 nm, H = 100 nm, θ = 10°, \({k_{\text{H}}}=7.1 \times {10^9}\) (Pa), \(D=0.5 \times {10^{ - 18}}\) (m2/s), and \(\zeta\) varying from undersaturation to oversaturation (Fig. 2b). The results show that the nanobubble grows when liquid is oversaturated (\(\zeta\) > 0). The experimental results qualitatively agree with numerical results when \(\zeta\) is about 0.15.

In particular, when we solve Eq. (5), we use size of the system L and H with other parameters. It implies that when nanobubble is confined in the nanoscale, size of system affects the nanobubble growth. To observe the role of system size for nanobubble growth, we calculate the growth dynamics of the nanobubble at various GLC size. Here we assume that H = L for setting simple geometry of system. Figure 3a shows that the growth dynamics is slowed down considerably when L < 100 nm and even nanobubble dissolves when L < 35 nm.

Fig. 3
figure 3

The gas oversaturation in the finite size system. a Temporal growth of nanobubble with initial radius 9 nm confined in the finite volume of the system. We change the length scale L of the system from 1000 nm to 20 nm. The initial concentration of gas is fixed with \({\zeta _\infty }\) = 0.15$. b The quantified finite size contribution, which is defined as the \(\zeta /{\zeta _\infty }\) for three different values of \({\zeta _\infty }\). The nanobubble growth gets slower when \(\zeta /{\zeta _\infty }\) decreases. Note that when \(\zeta /{\zeta _\infty }\) = 0, the growth of nanobubble completely stops and dissolution begins even \({\zeta _\infty }\) > 0

Full size image

We can quantify the relation between nanobubble growth and system size by rewriting Eq. (6) with the Eq. (3) and the Eq. (7) as

$$\zeta ={\zeta _\infty } - \frac{1}{{{c_{\text{s}}}}}\frac{{{N_{{\text{g}},{\text{b}}}}}}{{{N_{\text{l}}}}}$$
(8)

This equation explains that if the initial concentration is same, \(\zeta\) is always smaller than the \({\zeta _\infty }\) because \({N_{{\text{g}},{\text{b}}}}/{N_{\text{l}}}\) is nonzero and positive. And if we use relation \({N_{\text{l}}}=V\rho\), where \(\rho\) is the density of liquid molecule, this equation can explain why growth dynamics slow down as system size decreases, as shown in Fig. 3a. Notice that based on these results, it would be interesting to study the nanobubble growth dynamics by changing the concentration, but for this purpose, however, we should decrease the electron dose, which accompanies decrease of the detection resolution, limiting experimental observation of the bubble.

We can predict the growth dynamics of nanobubble in confined system with respect to the bulk system by adopting the relation \(\zeta /{\zeta _\infty }\), which has the maximum value 1 when \(\zeta ={\zeta _\infty }\) and size of GLC can be neglected. When \(\zeta /{\zeta _\infty }=0\), nanobubble begins to dissolve regardless of initial gas concentration. Figure 3b shows the plot of \(\zeta /{\zeta _\infty }\) as a function of L for three different \({\zeta _\infty }\) = 0.05, 0.15 and 0.25. When \({\zeta _\infty }\) = 0.15, \(\zeta /{\zeta _\infty } \leq 0\) at \(L \leq 35{\text{~nm}}\). This explains why the growth of nanobubble in Fig. 3a begins to dissolve at about L = 35 nm. When L > 100 nm, \(\zeta /{\zeta _\infty }\) ~ 1 which indicates that we can consider this system like a bulk.

The length scale of GLC in experiment is about L ~ 100 nm and here \(\zeta /{\zeta _\infty }\) ~ 1 (black dots in Fig. 3b). To observe the modified growth dynamics of nanobubble in the small system, one needs to decrease the system size and we may see it from the molecular dynamics (MD) simulation. MD simulation of nanobubble has been carried out in the small rectangular cell with L ~ 10 nm due to the limitation of computational resources (Weijs et al. 2012; Peng et al. 2013). For example, Peng et al. (Peng et al. 2013) used MD simulations to study about the formation of nitrogen nanobubble on the graphene interface. They used very high oversaturation \({\zeta _\infty }\) = 0.455, but failed to generate the spherical-cap nanobubble in the simulation cell. If we use Eq. (8) with consideration of the system size, \(V=6.9{\text{~}} \times 6.6{\text{~}} \times 7.0\) nm3 with other parameters \({k_{\text{H}}}=9.1 \times {10^{ - 9}}\), θ = 40°, and \({R_{\text{b}}}\) = 2 nm, then \(\zeta = - 0.329\) and it explains why nanobubble is not observed in the simulation cell. Because length of the MD simulation cell is about 10 nm length, \(\zeta /{\zeta _\infty }\) < 0 and growth of nanobubble is suppressed. To carry out the experiment for L < 50 nm, further work is needed to fabricate the controlled and smaller size of GLC. The works of Rasool (Rasool et al. 2016) and Kelly (Kelly et al. 2018) suggest that the size of GLC can be controlled using the nanopore with graphene encapsulation, as they observed the diffusion of nanomaterials in nanoconfined system.

Lastly, we discuss about the experimental diffusion coefficient with the order of ~ \({10^{ - 18}}\) m2/s, which is eight orders of magnitude smaller than the bulk diffusion coefficient. When we observe the nanobubble growth (Fig. 1), we can track their trajectories which moves the few tens of nm during 2 min and roughly estimate the order of diffusion coefficient (Temporal trajectory is shown in the Supplementary Fig. S2).

This slow moving of nanobubble may be associated with the sluggish surface water layer formed on the GLC surface: in the molecular scale, the water molecule near the solid surface directly interacts with the surface atom and forms the surface water layer, which has different hydrogen bonding structure and dynamics. As a result, its viscosity is a few orders higher than the bulk viscosity, as measured with the atomic force microscopy in the liquid environment (Kim et al. 2013; Ortiz-Young et al. 2013), and thus diffusion of nanobubble slows down under influence of surface water layer. Note that the damped diffusion of nanomaterials confined in the liquid cell has been generally observed in other studies (Chen et al. 2013; Lu et al. 2014), as well as our experiment.

In summary, we report direct observation of the nucleation and initial growth dynamics of nanobubbles inside the GLC via the in situ TEM observation. To elucidate the underlying mechanism of growth of the nanobubble against the large destructive Laplace pressure, we use the gas diffusion model considering the finite volume of GLC. The theoretical model well shows that oversaturation is the key factor of the observed nanobubble growth. Gas oversaturation has been considered dependent only on the gas concentration in conventional gas diffusion model. In our model, volume of GLC system is another factor, which increases the required amount of gas molecules for oversaturation and slows down the growth dynamics.

Methods

Fabrication of graphene liquid cell with Pt nanoparticle solution

To prepare the graphene-coated TEM grid, we prepared few layer graphene with 1 nm thickness, which is deposited on both sides of the copper substrate by chemical vapor deposition. We used oxygen plasma for 60 s to remove graphene layers deposited on the one side of the copper substrate. The copper substrate was etched in the freshly prepared etching solution for at least 12 h to remove the residual copper seeds, which left only the graphene floating on the etching solution-vapor interface. This floating graphene was transferred to deionized water and washed several times to remove any remaining contaminants and organic compound after etching. We then immediately placed the clean graphene on the TEM grid and dried for at least 1 h.

To fabricate the solution-encapsulating GLC, we prepared another clean graphene floating on the water in addition to the graphene-deposited TEM grid and nanoparticle solution. When we dropped 300 nL aqueous solutions of Pt nanoparticle on the graphene-coated TEM grid, the droplet firmly adhered to the graphene and thus did not fall down to the ground even when the grid was flipped. Using the flipped down TEM grid, we then placed gently the floating graphene in parallel to the water interface. When two graphene layers contact, surface tension of water breaks floating graphene to many smaller pieces. These small graphene pieces are attracted by the large graphene layer deposited on the TEM grid and forms the multiple GLCs with few µm size that contains the Pt nanoparticle aqueous solution. After this step, we held the GLC in ambient air at least overnight to completely remove the remaining unencapsulated liquid. Finally, the grid was loaded into the TEM sample holder and was ready for observation by TEM. The entire procedures and the TEM image of deposited GLC are shown in the Supplementary Fig. S1.

To measure the thickness of the GLC, we used log-ratio method (Malis et al. 1988), which determines the thickness L as

$$L= - \lambda \ln \left( {\frac{{{I_w}}}{{{I_0}}}} \right),$$
(9)

where \({I_w}\) and \({I_0}\) is the transmission intensity of GLC and bare graphene substrates, respectively, λ is the mean free path of inelastic scattering of water, 188.44 nm in this case. The thickness of GLC we used is around 100 nm.

For the preparation of Pt nanoparticle, the nanoparticle was synthesized with chloroplatinic acid [H2PtCl6(H2O)6, 99.9% pure on the metals basis] and polyvinylpyrrolidone (PVP) according to the literature (Kuhn et al. 2008). We first synthesized 2.9 nm Pt particles by dissolving PVP (66 mg) into the mixture of methanol (90 mL) and H2PtCl6(H2O)6 solution (10 mL of 6.0 mM), followed by refluxing for 2 h.

TEM Imaging

For TEM Imaging, we used JEOL 2100 TEM operating at an electron energy of 200 keV with 200 ~ 300 \({e^ - }{\AA^{ - 2}}\) electron dose rate per second for imaging in the liquid environment. Notice that with this dose rate, we could image the aqueous solvent system inside GLC with high enough contrast while avoiding radiation damage on the graphene substrate during 2-min observation. The lifetime of the GLC is around 3 min. We set the exposure time of 0.1 s, followed by the collection of fluorescent signal for 0.9 s, resulting in the frame time and temporal resolution of 1 s.