Introduction

The demand for energy from cleaner sources resulting from climate agreements and their associated targets has led countries to explore different energy options. The development of geothermal energy for electricity generation and predominantly the use of enhanced geothermal systems (EGS) are encouraging options, and it has the potential to be a major contributor in the future for energy sustainability according to the American Geoscience Institute (American Geosciences Institute 2020).

TT is located in the Southern Caribbean and has been producing oil and gas for over 100 years; however the hydrocarbon reserves have been steadily decreasing. According to the Worldmeter (Worldmeter 2021) in 1980, TTs average daily production was 200,000 barrels per day and today production has plummeted to roughly 55,000 barrels per day forcing the need for economic diversification away from hydrocarbons (Oil Now 2020). Industrialization in TT has resulted in the country having the second-highest per capita carbon dioxide emissions in the world which is about 6 times that of the world average (Indar 2019). Given TT’s large carbon dioxide footprint, a reduction in emissions has become a major issue regarding attention (Indar 2019). For more than 100 years, Trinidad and Tobago (TT) has been producing oil and gas and utilizes this as its main source of energy. According to Energy Snapshot (Energy Snapshot 2015), TT enjoys the lowest rates of electricity of US$0.04 per kilowatt-hour (kWh), due to applied subsidies on electricity by the government, while the rest of the Caribbean islands’ rates are an average of US$0.33 per kWh. It is suggested that without subsidies, the actual cost of electricity in TT would be $0.12 per kWh and that rates are set to rise (Chamber 2021) (Govinda Hosien 2020). As oil and gas production have steadily declined over the years, TT is currently considering removing these subsidies in an effort to make cleaner energy projects more feasible.

In keeping with TT Government’s Vision 2030 (Government of Trinidad and Tobago 2015), the Government has set an initial specific target for renewable energy of 10% of power generation by 2021 which is likely to grow further in an effort to reduce the emission of greenhouse gases which are very harmful to the air necessary for sustaining life (Marzolf 2015). This study will examine the possibility of using geothermal energy as a renewable source of energy for producing electric energy. The study will show the feasibility of TT adopting this method, similar to other countries in the world where the use of enhanced geothermal greatly increased their capability of producing geothermal energy.

Although TT does not have conventional geothermal reservoirs like the neighbouring Lesser Antilles, the island has mud volcanoes and abandoned oil and gas wells that can be retrofitted to harness geothermal energy. The fields of Heritage Petroleum Company Limited (Heritage), formerly Petroleum Company of TT Limited (Petrotrin) contain approximately 5000 abandoned wells in fields throughout the southern part of the island of Trinidad. These wells are ideal candidates for enhanced geothermal projects once the bottom-hole temperature is suitable, at least 40 to 73 degrees Centigrade and more importantly, the well bore integrity is in good order with the production capacity being suitable for the injection and production well requirement for EGS (Yao 2019). There are hundreds of abandoned oil wells at Forest Reserve (see Fig. 1), which have shut-in temperatures of approximately 100–115 °C (212–239 °F); a temperature gradient required for EGS applications.

Fig. 1
figure 1

Flow Chart outlining the Methodology

Full size image

The use of abandoned oil and gas wells was found to be economically feasible as drilling cost can account for 42 to 95% of the total cost for an enhanced geothermal system (Tester 1994). These wells will already have data on the lithology of the reservoirs, there are no drilling costs, projects using these wells avoid disrupting the environment (Yao 2019). Utilizing abandoned oil and gas wells near metropolitan zones would be least disruptive to communities (Sliwa 2014). Caulk and Tomac (Caulk 2017). Geothermal energy has been harnessed at locations with hydrogeological features (Caulk 2009). The depths of 1000 m together with thermal gradients between 4 and 7.3 degrees Centigrade per 100 m with bottom-hole temperatures between 40 and 73 degrees Centigrade exist in the abandoned wells in California, which are similar to the local Forest Reserve wells proposed in this study (Caulk 2009). Researchers developed their own mathematical model for enhanced geothermal systems or deep Borehole Heat Exchanger applications. Their model examined wells of depth 1000 m where it was shown that production fluids temperature can be higher than 40 degrees Centigrade with temperature gradients of up to 7 degrees Centigrade per 100 m. These parameters would allow low temperature direct use of enhanced geothermal systems for household heating, greenhouse heating and aquaculture use. There exist other examples of EGS feasibility using abandoned hydrocarbon wells (Davis 2009; Bu 2012; Templeton 2014 Nian 2018). Macenic and Kurevija (2017) Zhang (2008). The three (3) main parameters that determine the success of the production of geothermal energy are the temperature of the injected working fluid (water), the injection well pressure, and the distance between the injection well and producer wells (Sanyal and Butler 2005).

This study will involve the design, optimization and evaluation of the feasibility of an EGS for a more sustainable and environmentally friendly renewable energy production method for TT using wells from the Forest Reserve fields in South-western Trinidad as a case study. CMG software will be used to construct and optimize a base model which will be subjected to hydraulic fracturing. The economic feasibility of the optimal model will be evaluated.

Methodology

The implementation of the use of abandoned hydrocarbon wells is employed in this project. Three (3) injector wells and three (3) producer wells located in Forest Reserve Fields are utilized in the design process of the reservoir to harness the geothermal heat energy. The flow chart shown in Fig. 1 outlines the steps of the methodology.

Field description

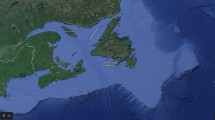
The Forest Reserve field, discovered in 1914, measures approximately 6773.88 acres and has hundreds of abandoned wells. Figure 2 shows a map of Southern Trinidad and the location of the Forest Reserve Field (Trinity 2021).

This area of interest is of upper Miocene to lower Pliocene periods in age and are deltaic in their origin. Structurally, the field is underlain by the western extremity of the East-North-East to West-North-West trending Debe-Wellington Anticline (Fig. 2). This plunges westward and is dissected by a series of extensional faults which tend to compartmentalize the fields and are sealed at most reservoir levels which can be seen in Figs. 3 and 4. The regional seals and stratigraphic marker horizons across the Forest Reserve field are the Upper Forest Clay and Lower Forest Clay.

Fig. 2
figure 2

A map of Southern Trinidad showing the location of Forest Reserve Field (Trinity 2021)

Full size image
Fig. 3
figure 3

A Structure Map of the area of interest, Forest Reserve Field

Full size image
Fig. 4
figure 4

A Net Oil sand map of the area of interest, Forest Reserve Field

Full size image

Mathematical modelling

A 3-D geothermal numerical model was designed to study the thermal recovery processes. Local thermal non-equilibrium is assumed. The retrofitted geothermal system utilizes energy equations to build the field temperature of the present fluid contained by the fractured rock matrix. The temperature field can then be employed to depict the method of heat transmission from the real rock-fluid throughout the heat retrieval process.

Mass conservation

The mass balance equation illustrates the fluid flow through an alterably porous media is set by Eq. 1 (Liang et al. 2016; Zhu 2016).

$$S\frac{\partial p}{{\partial t}} + \nabla . u = - \frac{\partial e}{{\partial t}} + Q$$
(1)

In Eq. 1, S, P, and t signifies the constricted specific storing of the media, pressure, and time, respectively; e signifies the volumetric strain, and Q signifies the source-sink of the outflow process. The water flow rate, u, can be determined by as it complies with Darcy’s Law of fluid flow:

$$u = - \frac{k}{\mu }\left( {\nabla p + \rho_{f} g\nabla z} \right)$$
(2)

where κ signifies the permeability of the saturated porous media; μ and ρf are dynamic viscosity and fluid density; g is gravitational acceleration; and the unit vector z signifies the course of gravity.

The mass balance equation for fractures is calculated using Eqs. 3 and 4 (Liang et al. 2016; Zhang et al. 2017).

$$d_{f} S_{f} \frac{\partial p}{{\partial t}} + \nabla t . u_{f} = - d_{f} \frac{\partial ef}{{\partial t}} + Qf$$
(3)
$$u_{f} = - d_{f} \frac{Kf}{\mu } \left( {\nabla_{t} p + \rho_{f} g\nabla_{t} z} \right)$$
(4)

where Sf, κf, df, and ef refer to the specific storage, permeability, thickness, and volumetric strain of the fractures, respectively; ∇τ indicates the gradient operator; and Qf, represents the fluid flow in the fractures and is given by,

$$Qf = - \frac{Kf}{\mu }\frac{\partial p}{{\partial m}}$$

where n signifies the standard course of the fracture surface.

The rock mass temperature field

The velocity of water in the rock matrix will be low as a result of a lowered porosity; thus, the water temperature is assumed to be corresponding to the rock temperature.

$$C_{s} \rho_{s} \frac{\partial Ts}{{\partial t}} = \lambda_{s} \nabla^{2} T_{s} + W$$
(5)

where ρs is the density of the rock; λs denotes the rock matrix thermal conductivity; Cs is the rock heat capacity; “W” signifies the heat exchange occurring in the reservoir; a negative sign refers to heat extracted from the rock, and a positive sign refers to heat captivated by the fluid.

The fracture water temperature field

$$d_{f} \rho_{f} C_{f} \frac{\partial Tf}{{\partial t}} + d_{f} \rho_{f} C_{f} . u_{f} \nabla_{f} T_{f} = d_{f} \nabla_{t} . \left( {\lambda_{f} \nabla_{t} T_{f} } \right) + W_{f}$$
(6)

In Eq. 6, ρf, Cf, and λf are the density, heat capacity, and water thermal conductivity, correspondingly; uf and Tf signify the velocity of the water flow and temperature of the water inside the fractures, correspondingly; Wf signifies the heat captivated by the water from the matrix block on the fractured surface (Zhang et al. 2017).

Throughout the interchange of heat among the water and the rock matrix and fractures, it is presumed that water follows Newton’s law of heat transfer. The heat flow from the rock to the fracture fluid (water per unit area) is described by Eq. 7 (Xu et al. 2015).

$$W = h\left( {T_{s} - T_{f} } \right)$$
(7)

When the convection efficiency h is sufficiently large, the rock temperature and water temperature become equal at the fracture surface.

Fluid properties under high temperature and pressure

The coupling effect is related to the fluid properties, and in the deep geothermal reservoirs under high enough temperature and pressure conditions the fluid density ρf (water density), which can be defined as a function of temperature and pressure (Xu et al. 2015), becomes variable and satisfies:

$${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\rho_{f} = 3.3086 - 0.899017\left( {4014.15 - T} \right)^{0.147166} - 0.39\left( {658.15 - T} \right)^{ - 1.6} \left( {p - 225.5} \right) + \delta }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{f} = 3.3086 - 0.899017\left( {4014.15 - T} \right)^{0.147166} - 0.39\left( {658.15 - T} \right)^{ - 1.6} \left( {p - 225.5} \right) + \delta }$}}$$
(8)

where δ is a function of water temperature T and pressure p; δ generally remains below 6% of 1/ρf and influences the dynamic viscosity μ = υρf, where υ represent the kinematic viscosity of water. The kinematic viscosity is defined by Eq. 9 (W 1983).

$${\varvec{\upsilon}} = \user2{ }\frac{0.01775}{{1 + 0.033{\varvec{Tf}} + 0.000221\user2{ T}_{{\varvec{f}}}^{2} }}$$
(9)

The fluid properties are affected by the temperature and can influence the thermal and hydraulic coupling processes within a reservoir.

The justification of a numerical model for thermo-hydraulic analysis has been performed in the previous work (Sun et al. 2017).

Initial and boundary conditions

Founded on the initial and boundary conditions, the heat production of the retrofitted geothermal system was simulated using the proposed model and the thermal hydraulic coupling analysis was run for 25 years (time step is 1 day). The selected initial and boundary conditions are given below:

Outflow field: To guarantee that water was circulated within the targeted reservoir, the pressure at the injection well was preserved at 1350 psi, and the production pressure was 1000 psi.

Thermal field: At the exterior thermal boundaries, the heat flux (QS) was constant; however the surface temperature at the injection well was 140 °F. The initial temperature in the reservoir was 212 °F for both water and rock.

Adopted parameters used in the computational processes

The data presented in Tables 1, 2, 3, 4, 5, 6, 7 show the actual and adopted parameters used in the computational processes.

Table 1 The well parameters (courtesy of Heritage Petroleum Company Ltd.)
Full size table
Table 2 The reservoir properties (courtesy of Heritage Petroleum Company Ltd.)
Full size table
Table 3 The adopted fracture information
Full size table
Table 4 The adopted properties for the reservoir
Full size table
Table 5 Adopted reservoir fluids characterization
Full size table
Table 6 The saturation inputs
Full size table
Table 7 The adopted relative permeability data for the fracture
Full size table

Appropriate assumptions were made to indicate key parameters and properties necessary to model an enhanced geothermal reservoir with fracturing parameters.

Thermal and hydraulic numerical model and simulation solution

After applying the initial and boundary conditions, the thermal and hydraulic coupling analysis was carried out and a 3D computational model was constructed based on actual and adopted geological parameters on half the field measuring approximately 3,386.94 acres (147,535,106.4 ft.) which can be observed in Fig. 5.

Fig. 5
figure 5

The geothermal exploitation model (unit: ft.)

Full size image

Thermal retrieval assessment method

Evans (2010) suggested and estimated the constraints used in the profitable utilization of a thermal reservoir: (1) the minimum reservoir temperature after 25 years of production, the reservoir temperature decline when deprived of restoration; (2) water loss is less than 10%; (3) the volume of reservoir restoration and (4) the area of the actual heat exchange. Sanyal SK (Sanyal and Butler, 2005) proposed that the three (3) most substantial statistics that are necessary to evaluate a thermal reservoir’s operation are the thermal recovery rate, temperature production, and net power production outlines.

Thermal retrieval runtime

Though geothermal energy is a renewable energy supply, the average project time period was carried out for 25 years on the base model then 25 years on the optimal and optimized models. The temperature of a fractured reservoir in a geothermal system after thermal retrieval could potentially decline severely and could take approximately 100 years to re-establish. Consequently, it is vital to combine the geothermal energy utilization to preserve viable expansion. Previous investigations have revealed that the optimal time to discontinue thermal retrieval is when the temperature declines by 10 °C or when the production well temperature has exhausted by 10%.

Optimization technique-hydraulic fracturing

Hydraulic fracturing is a favourable simulation procedure used in enhanced geothermal systems to upsurge heat production from a geothermal reservoir by increasing reservoir rock permeability. The objective is to construct a simulation model of an unconventional reservoir, Forest Reserve. The area is stimulated by hydraulic fractures is modelled using the Low Fidelity methodology. The construction and circulation of the hydraulic fractures follows the low fidelity methodology proposed by CMG. The low fidelity hydraulic fracturing modelling procedure is based on a guileless model that relays pressure with permeability or transmissibility. It is a basic method to a geomechanical model. It can be used in a single porosity or naturally fractured model, and it allows for the creation of a stimulated reservoir volume (SRV).

Carbon dioxide quantification equation

There are two main methods for estimating CO2 emissions from stationary sources, Direct Measurement and Fuel Input Analysis (Agency 2008). Fuel Input Analysis process was chosen for the application in this study and was utilized as described by (Boodlal 2014). The general equation used for the calculation is shown in Eq. 4 describing each component in the formula.

$${\text{Emissions}} = \varepsilon_{i = 1}^{n} {\text{Fuel}}_{i} \times {\text{HC}}_{i} \times {\text{C}}_{1} \times {\text{FO}}_{i} \times \frac{{{\text{CO}}_{{2\left( {m.w} \right)}} }}{{{\text{C}}_{{\left( {m.w} \right)}} }}$$
(10)

Eq. 10Where Fueli = Mass of Volume of Fuel Type i Combusted, HCi = Heat Content of Fuel Type i (Energy/Mass or volume of fuel), C1 = Carbon Content Coefficient of Fuel Type i (Mass C/Energy), FOi = Fraction Oxidized of Fuel Type I, CO2 (m.w.) = Molecular weight of CO2, C (m.w.) = Molecular Weight of Carbon.

Economic analysis

Discounted Net Cash Flow (DNCF) is an appraisal technique used to approximate the value of an asset based on its predictable future cash flows (Investopedia 2021). DNCF analysis tries to calculate the worth of an asset today, based on forecasts of future money generation. This applies to the choices of investors in companies or securities, such as acquiring a company, and investing in a technology startup. Below shows the formula used to calculate the DNCF.

Equation to Calculate the DNCF (Investopedia 2021)

$${\text{Discounted}}\,{\text{Net}}\,{\text{Cash}}\,{\text{flow}}({\text{DNCF}}) = {\text{Net}}\,{\text{Cash}}\,{\text{flow}}/(1 + r)^{n}$$

where ‘r’ is the minimum acceptable rate of return and ‘n’ is the number of years.

Results and discussion

Analysis of the production of geothermal energy

The three (3) main parameters that determine the success of the production of geothermal energy are the temperature of the injected working fluid (water), the injection well pressure, and the distance between the injection well and producer wells. Sensitivity simulation analyses were carried out using the initial conditions as can be seen in Tables 1, 2, 3, 4, 5, 6, 7 model to obtain the optimal model for the project.

In terms of the injection stream temperature (°F) sensitivity

The lifecycle and production performance of a retrofitted abandoned well, or a retrofitted geothermal reservoir, are intensely reliant on the surface temperature of the production well. In a retrofitted geothermal system, the temperature of either the injected or the re-injected fluid heavily reliant on the heat transfer into the reservoir, which results in higher production performance and longer lifetime. It should be noted that the use of too high of an injection temperature can cause damage to the well assembly and bottom hole equipment. Although high-quality metals are used to manufacture the equipment, a high injection temperature over a longer period deteriorates the bottom hole assembly. On the reverse, if the injection temperature is too low, heat flow into the subsurface thermal environment is inadequate to permit the heat flow to attain the preferred quality. Figure 6 shows the evolution of the enthalpy produced utilizing different stream temperatures (77 °F, 104 °F, 122 °F, 140 °F, and 158 °F) to evaluate the output temperature with respect to time while keeping other inputs constant as can be seen in the previous Tables 1, 2, 3, 4, 5, 6, 7. It can be seen that each variable increases a linear manner till 2047. The chosen temperature is 140 °F due to aforementioned points and due to high possibility of utilizing produced water with the approximately the temperature, 140 °F. Having a high initial temperature is vital to the success of the project due the necessary provision of sufficient heat energy to be converted into electrical energy to provide electricity to the designated areas. With that being stated, the type of geothermal plant is highly dependent on the temperature range of the heat being produced from such project. The output temperature was recorded at 210 °F using an injection temperature of 140 °F.

Fig. 6
figure 6

The evolution of the enthalpy using different stream temperatures throughout the 25-year study period. (Unit: Btu)

Full size image

Injection pressure (psi) sensitivity

Extremely high injection rates, i.e., higher than a fracture pressure of 1574.5 psi, can result in a premature thermal break between the injection and production wells caused by earlier commencement of the convective process in an open loop geothermal system (Hongmei Yin, 2021). Therefore, the injection rate must not be too great unless the intention is to induce fractures within the reservoir. Figure 7 shows the evolution of the enthalpy using different injection pressures (800 psi, 1000 psi, 1200 psi, and 1400 psi) throughout the 25-year study period. From the graph, it can be seen that at 1000 psi, 1200 psi, and 1400 psi, the enthalpy increased in a stable linear manner reaching different amounts. The necessary pressure required to create connective flow with the time allocated for the heat transfer from the reservoir to the water to produce hot water can be the cause of the vast differences seen in Fig. 7. At 800 psi, the enthalpy can be noted as negligible and assumed that the pressure was too low to create the convective process and able to penetrate the reservoir to create a pathflow. An injection pressure of 1400 psi was chosen due the best results produced yet not nearing the fracture pressure (Table 8).

Fig. 7
figure 7

The evolution of the enthalpy using different injection pressures throughout the 25-year study period. (Unit: Btu)

Full size image
Table 8 The CO2 emissions from electricity generation (Administration 2019)
Full size table

Well spacing sensitivity

The set time and quantity of heat exchange were significantly subjective by the distance between the injector and producer wells. An appropriate distance between the injection and production wells is essential to evade a thermal breakthrough. If the distance between the injection and production wells is too great, water loss is possible, but the energy exchange between the rocks and fluid will be adequate. An injection well too nearby to the production well will result to a premature thermal development, as a result of a lower flux of heat between the rocks and the fluid (Jung, 2012). Therefore, the distance between the injection and production wells plays a critical part in the working lifespan and performance of the system. Figure 8 shows the evolution of the enthalpy using different well spacings (1200ft, 1400ft, 1600ft, and 1800ft) throughout the 25-year study period. Each variable showed a constant stable linear increase in Fig. 8. Note that the differences are minuscule due the distances being not of a great variance. The well distance of 1600 ft was chosen due it being the furthest from each other without stepping out of the set boundary of the field.

Fig. 8
figure 8

The evolution of the enthalpy using different well spacings throughout the 25-year study period. (Unit: Btu)

Full size image

Optimal model design (retrofitted geothermal system)

Based on the sensitivity analyses conducted earlier, an injection temperature of 140o F, an injection pressure of 1400 psi, and a well spacing of 1600 ft were utilized to design the optimal model for application at the Forest Reserve, Trinidad. From Fig. 9, it can be seen that the enthalpy produced in a constant stable linear manner to approximately 2.9E + 12 Btu. It should be noted that by utilizing the sensitivity analysis process, the optimal model shown, in Fig. 9, produced the highest enthalpy when compared to Fig. 6, 7 and 8 thus demonstrating the importance of the each sensitivity variable.

Fig. 9
figure 9

The evolution of the enthalpy throughout the 25-year study period. (Unit: Btu)

Full size image

The total production of energy prominently relies on the surface production temperature that exemplifies the output temperature connection with the energy harnessed out of the system. In Fig. 9 the operation can be seen to be acting in a steady increasing phase throughout the twenty-five (25) year period and peaked at 2.9E + 12 Btu. This pattern demonstrates that the retrofitted geothermal system can be successful for the full twenty-five (25) years for thermal recovery runtimes and provide another form of harnessing electricity.

Hydraulic fracturing with injection pressure sensitivities

Hydraulic fracturing was applied to the optimal model design obtained to enhance heat recovery. This was done by utilizing a Form Factor (ff) of 2500 and alternating the surface water rate (bbl/day) then stopping, equating to zero (0) bbl/day using cold water to induce permanent fractures in the formation during the first fifteen (15) days of production shutting in the well. An injection pressure was calculated using the reference depth of 2250 ft multiplied by an estimated fracture gradient of 0.7 psi/ft resulting in 1574.5 psi. Thereafter, injection pressures higher than the fracture pressure of 1574.5 psi were utilized. Figure 10 shows the corresponding enthalpy production using different hydraulic fracturing pressures (1650 psi, 1800 psi, and 2000 psi) throughout the 25-year study period. It can be seen that even though 1650 psi and 1800 psi are greater than the fracture pressure of 1574.5 psi, they both produced quite lower than at 2000 psi. This could be assumed as the pressure only fractured around the injection wellbore and not further into the reservoir. Also this is exposes the fracture gradient can be of a higher value and not estimated at 0.7 psi/ft. This theory could be proven in a leak-off test but was not done performed. Therefore the pressure of 2000 psi was chosen to move forward as it showed significant results.

Fig. 10
figure 10

The evolution of the enthalpy using different hydraulic fracturing pressures throughout the 25-year study period. (Unit: Btu)

Full size image

Comparison of optimal EGS model to optimized EGS model, 25-year lifecycle

Figure 11 shows the comparison of the optimal model and the optimized (hydraulic fracturing) model evolution of the enthalpy produced throughout a 25-year period. It shows a lower enthalpy in the hydraulic fracturing model when compared to the optimal model. Both models produced in a steady state till 2047. The purpose of Fig. 11 is to decide the best model/procedure appropriate for the reservoir to produce the superlative results. Unfortunately, due to the shallow nature of the field at present, hydraulic fracturing would not be recommended due to depth, possible the loss of water into the formation, more water being force into the reservoir resulting in less time for the heat transfer to occur, and the possibility of the induced fracture not travelling in the desired direction due to the reservoir type being sandstone.

Fig. 11
figure 11

The comparison of the optimal EGS model to optimized EGS model evolution of the enthalpy throughout the 25-year study period. (Unit: Btu)

Full size image

Figure 12 demonstrates the comparison of the optimal model and the optimized model’s average formation temperature over a 25-year period. It shows the optimal model producing a lower formation temperature at 205.3 °F at the end of the 25-year period when compared to the optimized retrofitted system that resulted to 206.1 °F. Both models demonstrated a linear decline. This linearity is due to the constant heat supply due to the system’s stable temperature (i.e., it remained within the maximum and minimum values). An almost instantaneous dip in temperature can be seen in the optimized model when the hydraulic fracturing was implemented for the first 15 days then the temperature increased back the ‘standard’ level in the generated graph. From the data produced the recommendation would be to implement the optimal retrofitted system.

Fig. 12
figure 12

The evolution of the comparison of the optimal EGS model to the optimized EGS model average formation temperature throughout a 25-year period. (Unit: °F)

Full size image

Size and type of applicable plant

Below shows the calculation done to calculate the production capacity of the plant. The calculation utilizes the peaked cumulative enthalpy produced from the optimal model to generate the potential baseload electricity, Watts per second.

  1. 1.

    Peaked Enthalpy Cumulative after 25 years, Btu = 2.8E + 12 Btu

  2. 2.

    Enthalpy Btu converted to Enthalpy, Joules = 2.8E + 12 × 1055 = 2.954E + 15 J

  3. 3.

    Joules converted to Mega Joules = 2.954E + 15/1E + 6 MJ = 2.954E + 09 MJ

  4. 4.

    Plant Life, 25 years to seconds = 25 × 365 × 24 × 3600 = 788,400,000 s

  5. 5.

    Plant Capacity = 90%

  6. 6.

    Joules converted to Joules per seconds = 2.954E + 15/788,400,000 = 3,746,829.021

  7. 7.

    Joules/second = Watts/second = 3,746,829.021 W/s

  8. 8.

    Watts per second converted plant size = 3,746,829.021 × 0.9 = 3,372,146.119 W/s

    = 3.3721 MWe

Given that the reservoir temperature is approximately 212 °F, the appropriate and applicable plant type to Trinidad’s context would be the installation of a Binary Open Loop Cycle Plant with the addition of a separation tank. A separation tank is required in the installation aspect of the project due to the possibility of producing hot water with oil that could potentially cause damage to the heat exchanger. Using the size of the plant calculation, the binary open-loop cycle plant has the potential to be in operation for 25 years providing 3.3721 MWe of base-load power which possess the potential to supply constant electricity to approximately 2200 houses within the district of the proposed plant. Though the capacity of the plant seems small, the feasibility of the project is explored in the economic evaluation. There are a few small geothermal plants that exists worldwide such as Guadeloupe (4.5 MW), Taiwan (0.3 MW), Thailand (0.3 MW), Austria (1.2 MW), Australia (1.7 MW), Hungary (3 MW), Belgium (0.8 MW) and Ethiopia (7.3 MW) (Huttrer 2020).

This type of operation can potentially result in a breakthrough for TT and the Caribbean as it will be the first retrofitted geothermal system to be launched in the region. This project can also reveal new employment opportunities and comply with the agreement as was signed from the Government of TT in 2018 (Government Ratifies Paris Agreement 2018). The power plant would require a turbine, generator, a cooling tower, the 3 injection wells, the 3 production wells and a Separation tank. A rough estimate of plant size would require 1–8 acres per MW, therefore using the highest case scenario of 8 acres per MW would result in approximately 26.496 acres.

Carbon dioxide emission reduction

Referencing Table 8, the CO2 emission rate produced from natural gas is approximately 0.92 lbs/kWh (Administration 2019) while a Binary Open-Loop Cycle Plant emits 0.1 lbs/kWh (Scientist 2013). Figure 13 was constructed to demonstrate the average annual carbon dioxide emission reduction that can be generated from the implementation of the Binary Open-Loop Cycle Plant for a 25-year lifecycle of the proposed plant lifecycle (highlighted in red). This was done using the annual cumulative enthalpy production, Btu, converted into kWh to provide the annual total heat production of the optimal model. 1 Btu is equal to approximately 0.000293071 kWH (Bureau International des Poids et Mesures 2019). The enthalpy production was then multiplied by the respective factors, CO2 emissions produced from a binary plant (0.1 lbs/kWh), and from natural gas generated electricity (0.92 lbs/kWh). The Difference between the Binary Open-Loop and Natural Gas carbon dioxide emission revealed the approximate reduction in CO2 gas being emitting from the generation of electric energy. The idea is to estimate the amount of CO2 emissions produced from replacing the natural gas generated electricity with geothermal energy (a cleaner, and renewable energy source) to obtain the reduction of CO2 emissions. The Cumulative annual carbon dioxide reduction was estimated to be approximately 1.00125E + 11 lbs which is equivalent to 50,062,500 tons of carbon dioxide after a 25-year period. An approximate 88.9% reduction of CO2 from replacing 3.3721 MW of natural gas generated electricity with 3.3721 MW of enhanced geothermal electricity. This reduction in CO2 will result in a cleaner and renewable way of producing electricity not affected by meteorological conditions, therefore reducing the country’s carbon footprint.

Table 9 The parameters used in the economic analysis
Full size table

Economic analysis

Geothermal energy is often misinterpreted to be an expensive source of electricity. Though it may be true, geothermal power plants require a substantial amount of initial capital and some government assistance in the early stages. The overall and operating costs of geothermal power are significantly lower than other technologies (Gawell 2014). The geothermal power plant has no fuel costs and minimal maintenance or ancillary costs. Once the plant begins operations, it can generate electricity for 30 years or longer given if the field is engineered and maintained sustainably (Gawell 2014).

Table 9 shows the production of Kwh per year for a 25-year period with the cost of geothermal electricity, US$ and its corresponding CAPEX, Capital Expenditure and OPEX, Operating Expenditure. Due to the nature of this project, CAPEX reduced by approximately 50%. The approximate cost of setting up a geothermal plant is roughly US $2–$7 MM per Megawatt. Using this information, the highest case scenario of US$7MM was chosen. That figure was then multiplied by 3.3721 MW totalling the cost to US$23.6MM. Now, this US$23.6MM was divided half and rounded off to give $12MM US.

Well workovers are required to retrofit these wells to harness the geothermal energy. The cost of setting up a small Binary Cycle plant with a separation tank is also included. The OPEX is approximated to cover maintenance, repairs, and salaries for the employees. A simple economic analysis using appropriate assumptions was carried out. Utilizing Crystal Ball, Monte Carlo sensitivities were done to show the feasibility of the project (Fig. 13).

Fig. 13
figure 13

Cumulative carbon dioxide emission reduction from the difference in the optimal model and natural gas generated electricity

Full size image

Table 10 demonstrates the cash flows for the project. Cash inflows are calculated using the production multiplied by the price and the Cash Outflows are calculated by the addition of CAPEX and OPEX. The Net Cash flow is the difference between the Inflow and Outflow leaving the remainder. The Remainder is the monetary value the project is generating, USD $6,195,808,168 for the 25-year period, highlighted in yellow.

Table 10 Cash flows for the proposed project
Full size table

Table 11 shows the Internal Rate of Return of 190% and the payback period in January, 2024 highlighted in yellow once production starts in January, 2023. A positive IRR indicates that the project is indeed feasible. IRR is calculated by taking the difference between the current or expected future value and the original beginning value, divided by the original value and multiplied by 100 (Investopedia 2021). The payback period is equal to Initial investment divided by Cash flow per year (Investopedia 2021).

Table 11 The IRR and payback period
Full size table

Utilizing a Minimum Rate of Return of 10%, means the company is willing to accept a minimum of 10% of the return which summed up to US$1,431,263,840.00 which can be seen in Table 12. A positive NPV, Net Present Value, implies that the investment is generating a rate of return which is greater than the MARR of 10%. Utilizing Crystal Ball, Monte Carlo simulations were done to obtain the feasibility of the project. The assumption variables are (1) Price, US$0.05–0.10 per kWh, with US$0.05 per kWh being the likeliest (2) CAPEX, US$10-14MM with US$12MM being the likeliest, and (3) OPEX, US$1-3MM with US$2MM being the likeliest. The defined forecast used an excel generated IRR of 190% and NPV of US$1,431,263,840. The IRR forecast revealed that it has a 100% certainty of obtaining higher than a MARR of 10% showing that the project again is indeed feasible.

Table 12 The DNCF and Interest using 10% MARR
Full size table

Conclusion

A generic model was constructed using actual and adopted geological parameters and data using three (3) injector and three (3) producer wells with a recorded temperature of 212 \(^\circ{\rm F}\) for a 25-year time period. The optimal model resulted in a maximum enthalpy cumulative value of 2.8E + 12 Btu for a time period of 25 years. Hydraulic fracturing of the optimal model was conducted and the results revealed the optimum injection pressure should be 2000 psi to provide a maximum enthalpy cumulative value of 2.6E + 12 Btu. It was demonstrated that the optimal model, produced a slightly higher enthalpy of 0.2E + 12 Btu. The plant capacity was calculated to be 3.3721 MW using a binary open-loop cycle requiring a land space of approximately 26.496 acres. Using the cumulative enthalpy production, the carbon dioxide average reduction of 50,062,500 tons of CO2 after the 25-year period. An economic analysis of the project found an IRR of 190% and an NPV of US$1,431,263,840.00 utilizing a MARR of 10%, CAPEX of US$12MM, OPEX of US$2MM and a cost of geothermal electricity at US$0.05 per kWh. These results were then used in Crystal Ball to apply Monte Carlo simulations where it confirms that the project is 100% economically feasible.