Introduction

Formation collapse pressure and formation fracture pressure are the upper and lower limits of safe drilling fluid density window to maintain wellbore stability. How to accurately predict and describe formation collapse and fracture pressure are an important content to avoid wellbore instability risk (Tinggen and Zhichuan 2000; Ottesen et al. 1999). With the development of drilling to deep well complex formation and deep water, the geological environment encountered in the process of drilling is becoming more and more complex. In the actual drilling engineering, due to the particularity of the drilling engineering construction, as well as the uncertainty of geological conditions, the complexity of operating environment factors, the variability of construction methods and design parameters, etc., many uncertain factors will be encountered from time to time in the process of drilling construction. It is increasingly difficult to accurately predict formation collapse and fracture pressure. The rock mechanics parameters and in-situ stress input in the existing calculation model of formation collapse and fracture pressure are all treated according to the fixed value, and the prediction results of formation collapse and fracture pressure are all single value results. This method ignores the error between the prediction result and the actual result due to the uncertainty of the input parameters of the calculation model of collapse and fracture pressure (Guangfu et al. 2019; Kolawole et al. 2018; Moos and Peska 2003). The in-situ stress and rock mechanics parameters in the calculation model need to be calculated based on the indirect formula according to the seismic or logging data, and there is uncertainty (Mostafavi et al. 2011; Zhide , 2004; Limin et al. 2017). The design based on the inaccurate prediction results may lead to the risk of wellbore instability. In order to solve this problem, this paper proposes a quantitative characterization method of formation collapse and fracture pressure uncertainty based on Monte Carlo simulation. First of all, established and improved the existing calculation model of formation collapse and fracture pressure. On this basis, analyzed the sources of uncertainty in the calculation model of formation collapse and fracture pressure, mainly the in-situ stress and rock mechanics parameters, which are usually obtained through indirect mathematical model calculation based on seismic or logging data, so there are a lot of uncertainties. After that, the uncertainty of rock mechanical parameters and in-situ stress is analyzed, and its probability distribution is determined. Finally, based on Monte Carlo simulation, the quantitative characterization method of the uncertainty of formation collapse and fracture pressure is established. The prediction result of formation collapse and fracture pressure is not a single curve or value, but an interval range, which is more practical for drilling in complex geological environment.

Methods

Quantitative calculation model of collapse and fracture pressure

Formation collapse and fracture pressure are the upper and lower limits of safe drilling fluid density window to maintain wellbore stability (Yi et al. 2019). How to accurately predict and describe formation collapse and fracture pressure are an important content to avoid wellbore instability risk. In the calculation of formation collapse and fracture pressure, many key calculation parameters affect the results, mainly including in-situ stress and rock mechanics parameters, which can be calculated based on logging data or seismic interpretation data.

  1. (1)

    Rock mechanics parameters

    Rock mechanics parameters can be divided into mechanical properties and elastic properties (Xiangjun and Pingya 1999; Min et al. 2009).

  2. a.

    Rock elastic properties

    P-wave velocity of rock:

    $$ V_{p} = \frac{{E_{d} \left( {1 - \mu_{d} } \right)^{0.5} }}{{\left[ {\rho_{d} \left( {1 + \mu_{d} } \right)\left( {1 - 2\mu_{d} } \right)} \right]^{0.5} }} = \frac{1}{{\Delta T_{p} }} $$
    (1)

    S-wave velocity of rock:

    $$ V_{s} = \frac{{E_{d}^{0.5} }}{{\left[ {2\rho_{b} \left( {1 + \mu_{d} } \right)} \right]^{0.5} }} = \frac{1}{{\Delta T_{s} }} $$
    (2)

    In formula, ΔTp—Rock P-wave time difference, us/m. ΔTs—Rock S-wave time difference, us/m. ρb—Rock density, g/cm3. Ed—Dynamic Young's modulus, MPa. ud—Dynamic Poisson's ratio, dimensionless.

    The transformation relationship between each rock elastic parameters:

    $$ G = \frac{E}{{2\left( {1 + \mu _{d} } \right)}}K_{b} = \frac{E}{{3\left( {1 - 2\mu _{d} } \right)}}C_{b} = \frac{1}{{K_{b} }} $$
    (3)

    In formula, E—Young's modulus, MPa. G—Shear modulus, MPa. Kb—Bulk modulus of elasticity, MPa. Cb—Volume compression coefficient, dimensionless.

    The elastic parameters of rock can be divided into dynamic and static parameters, which can better reflect the real elastic characteristics of rock. In practical application, the dynamic elastic parameters should be converted into static elastic parameters.

  1. ①

    Dynamic elastic parameters

    According to formula (1), formula (2) and formula (3), the elastic parameter formula of dynamic rock mechanics is derived, as shown in Table 1

    Table 1 Calculation formula of dynamic elastic parameters
    Full size table
  2. ②

    Conversion of dynamic and static elastic parameters

    The transformation relationship between dynamic and static elastic parameters (Min et al. 2009):

    $$ \mu _{s} = A_{1} + K_{1} \mu _{d} \;E_{s} = A_{2} + K_{2} E_{d} $$
    (4)

    In formula, \({\text{A}}_{1} = {\text{a}}_{11} + {\text{a}}_{12} \lg (\sigma_{1} - \sigma_{3} )\)、\({\text{A}}_{2} = {\text{a}}_{21} + {\text{a}}_{22} \lg (\sigma_{1} - \sigma_{3} )\)、\({\text{K}}_{1} = {\text{k}}_{11} + {\text{k}}_{12} \lg (\sigma_{1} - \sigma_{3} )\)、

    \({\text{K}}_{2} = {\text{k}}_{21} + {\text{k}}_{22} \lg (\sigma_{1} - \sigma_{3} )\), σ1 and σ3 are the maximum and minimum principal stresses, respectively. a11、a12、a21、a22、k11、k12、k21、k22 are regression coefficients. The above transformation relationship needs to be obtained according to the core laboratory experiments.

  1. b.

    Rock mechanical properties

    The calculation formula of mechanical properties is shown in Table 2.

    Table 2 Calculation formula of rock strength parameters
    Full size table

    In table, ρ—Rock density, g/cm3. Vcl—Shale content, dimensionless. ϕ—Internal friction angle, °. M = a-b × C. a、b—The coefficients related to rock properties are obtained by inverse calculation of core test experiments.

  2. (2)

    In-situ stress

    The commonly used calculation formula of in-situ stress is (Mian et al. 2008):

    $$ \sigma_{v} = \int {G_{o} d{\text{H}}} $$
    (5)
    $$ \left\{ \begin{gathered} \sigma_{H} = \frac{{\beta_{1} E + 2\mu (\sigma_{v} - \alpha G_{p} )}}{2(1 - \mu )} + \frac{{\beta_{2} E}}{2(1 + \mu )} + \alpha G_{p} \hfill \\ \sigma_{h} = \frac{{\beta_{1} E + 2\mu (\sigma_{v} - \alpha G_{p} )}}{2(1 - \mu )} - \frac{{\beta_{2} E}}{2(1 + \mu )} + \alpha G_{p} \hfill \\ \end{gathered} \right. $$
    (6)

    In formula, σv—Vertical stress, MPa. σH—Maximum horizontal in-situ stress, MPa. σh—Minimum horizontal in-situ stress, MPa. u—Poisson's ratio, dimensionless. E—Young's modulus, MPa. H—Well depth, m. Gp—Pore pressure, MPa. β1、β2—Coefficient of tectonic stress:

    $$ \left\{ \begin{gathered} \beta_{1} = \frac{{(1 - \mu )(\sigma_{H} + \sigma_{h} ) - 2\mu (\sigma_{v} - \alpha G_{p} ) - 2\alpha (1 - \mu )G_{p} }}{E} \hfill \\ \beta_{2} = \frac{{(1 + \mu )(\sigma_{H} - \sigma_{h} )}}{E} \hfill \\ \end{gathered} \right. $$
    (7)

    In formula, the maximum and minimum horizontal in-situ stress can be measured by various in-situ stress measurements. Other parameters are calculated according to logging data.

  1. (3)

    Collapse pressure

    The commonly used calculation formula of formation collapse pressure is based on the Mohr–Coulomb strength criterion (Mian et al. 2008):

    $$ \rho_{c} = \frac{{\eta (3\sigma_{H} - \sigma_{h} )}}{{(K^{2} + \eta )}} + \frac{{\alpha \rho_{p} (K^{2} - 1)}}{{(K^{2} + \eta )}} - \frac{2CK}{{{0}{\text{.00981}} \times H \times (K^{2} + \eta )}} $$
    (8)

    In formula, ρc—Collapse pressure, g/cm3. H—Well depth, m. K = cot(45°-ϕ/2). ϕ—Internal friction angle, °. C—Rock cohesion, MPa. ρp—Pore pressure, g/cm3. σH—Maximum horizontal in-situ stress, g/cm3. σh—Minimum horizontal in-situ stress, g/cm3. \(\eta \)—Nonlinear correction coefficient of stress. α—Biot coefficient.

  1. (4)

    Fracture pressure

    The commonly used calculation formula of fracture pressure is (Qining 1983):

    $$ \rho_{f} = 3\sigma_{h} - \sigma_{H} - \alpha \rho_{p} + {\raise0.7ex\hbox{${S_{t} }$} \!\mathord{\left/ {\vphantom {{S_{t} } {0.00981 \times H}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${0.00981 \times H}$}} $$
    (9)

    In formula, ρf—Fracture pressure, g/cm3. St—Uniaxial tensile strength, MPa.

Analysis of uncertainty sources of collapse and fracture pressure

According to the calculation model of formation collapse and fracture pressure, the parameters in the calculation model can be divided into three categories: well trajectory parameters, in-situ stress and rock mechanical parameters. Among them, the well trajectory can be accurately obtained according to drilling design or MWD data. The in-situ stress and rock mechanical parameters are usually calculated by indirect mathematical model based on logging or seismic interpretation data, so there are a lot of uncertainties. For the drilled well, the in-situ stress and rock mechanics parameters can be obtained by various logging data or seismic data. However, it is difficult to obtain these parameters accurately before drilling, which will lead to a large error or uncertainty in the pressure prediction results of the well to be drilled. Therefore, it is necessary to analyze the uncertainty of rock mechanical and in-situ stress parameters. Using the interpretation results of logging data to estimate the probability distribution of parameters, the interpretation results of formation collapse and fracture pressure with uncertainty are finally obtained.

Quantitative characterization of collapse and fracture pressure uncertainty

Quantitative characterization of in-situ stress and rock mechanical parameters

In order to analyze the uncertainty of rock mechanical parameters and in-situ stress and determine its probability distribution, it is necessary to establish the sample database of rock mechanical parameters and in-situ stress parameters. According to sequence stratigraphy (Yinye 2009): "under the same geological period and sedimentary conditions, the rocks have the same lithology, which will produce similar seismic or logging responses." Therefore, we select the logging interpretation results of rock mechanics parameters and in-situ stress within a certain depth of the same formation as samples and build the sample database. It is assumed that there are 2n + 1 log interpretation results of rock mechanical parameters and in-situ stress in the range of well depth ΔH. They are treated as a set of measurement samples, as shown in Fig. 1.

Fig. 1
figure 1

Diagram of rock mechanics parameters and in-situ stress analysis sample

Full size image

ΔH is the sample interval, and its value is twice the range of theoretical variogram model in the sample formation group. Then, the probability distributions of rock mechanical parameters and in-situ stress are calculated by using normal information diffusion estimation theory (Yifeng et al. 2016; Shushen 2001). The probability density functions of rock mechanical parameters and in-situ stress X are assumed to be f(x). Finally, the normal information diffusion of f(x) is estimated as follows:

$$ \tilde{f}_{i} (x) = \frac{1}{{\sqrt {2\pi } (2n + 1)h}}\sum\limits_{j = i - n}^{i + n} {\left\{ {\exp \left[ { - \frac{{\left( {x - x_{j} } \right)^{2} }}{{2h^{2} }}} \right]} \right\}} $$
(10)

In formula, h—Diffusion coefficient, m.

$$ h = \frac{{\lambda \left( {x_{\max } - x_{\min } } \right)}}{2n} $$
(11)

In formula, xmax、xmin—The maximum and minimum value of rock mechanical parameters and in-situ stress X in the target formation. The coefficient λ can be obtained according to Table 3:

Table 3 Corresponding relation between λ and sample number (2n + 1)
Full size table

Quantitative characterization of collapse and fracture pressure uncertainty

The steps to quantify the uncertainty of collapse and fracture pressure based on Monte Carlo simulation (Sundar and Witt 1995; Junhu 2007) are as follows:

  1. (1)

    Determination of the rock mechanical parameters and in-situ stress probability distributions. According to the above method, the analysis sample database of model input parameters at any depth h position is constructed: \(F_{N} \sim f(x_{1} ),f(x_{2} ), \cdot \cdot \cdot ,f(x_{n} )\)

  2. (2)

    Construction of random simulation sample sets. The random values are generated according to the probability distribution of the rock mechanical parameters and in-situ stress. The collapse and fracture pressure at any depth can be obtained by substituting them into the calculation models.

  3. (3)

    Construction of collapse and fracture pressure sample sets. The probability distribution and cumulative probability distribution function of formation collapse and fracture pressure at any depth are obtained by selecting normal distribution form to fit the statistical analysis calculation results: fh(Pt,f)、Fh(Pt,f).

  4. (4)

    Quantitative characterization of collapse and fracture pressure uncertainty. Through the above methods, the cumulative probability of collapse and fracture pressure at different depths can be obtained, which can form the set:

    $$ F(P_{t,f} ) = \left\{ {F_{{h_{1} }} (P_{t,f} ),F_{{h_{2} }} (P_{t,f} ),F_{{h_{3} }} (P_{t,f} ),...,F_{{h_{i} }} (P_{t,f} ),...,F_{{h_{n} }} (P_{t,f} )} \right\} $$
    (12)

    In formula, \((P_{t,f} )_{{h_{i}, j }}\)—The collapse and fracture pressure with cumulative probability j at the depth of hi. Take the same cumulative probability value j0 to form the new set:

    $$ (P_{t,f} )_{{j_{0} }} = \left\{ {(P_{t,f} )_{{h_{0} ,j_{0} }} ,(P_{t,f} )_{{h_{1} ,j_{0} }} ,(P_{t,f} )_{{h_{2} ,j_{0} }} ,...,(P_{t,f} )_{{h_{i} ,j_{0} }} ,...,(P_{t,f} )_{{h_{n} ,j_{0} }} } \right\} $$
    (13)

    In formula, \((P_{t,f} )_{{j_{1} }}\)\((P_{t,f} )_{{j_{2} }}\)—The collapse and fracture pressure with cumulative probability j1、j2 (j1 < j2). The two curves constitute the interval of collapse and fracture pressure with a confidence of \(\left| {j_{1} - j_{2} } \right| \times 100\%\), which indicates that the probability that the actual collapse and fracture pressure in \(\left[ {(P_{t,f} )_{{h_{i} ,j_{1} }} ,(P_{t,f} )_{{h_{i} ,j_{2} }} } \right]\) is \(\left| {j_{1} - j_{2} } \right| \times 100\%\).

Results and discussions

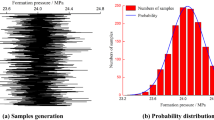
Well XX is a deep shale gas exploration well in South Sichuan work area, taking XX as an example for analysis. Firstly, the probability distributions of rock mechanical parameters and in-situ stress at any depth are calculated. Table 4 shows the calculation results of parameter probability at the depth of 2000 m. Then, the probability distributions of collapse and fracture pressure at this depth are obtained, as shown in Fig. 2 and Fig. 3. Finally, the interval profile of collapse and fracture pressure with 90% confidence is obtained by programming calculation, as shown in Fig. 4.

Table 4 Probability distribution characteristic parameters of each parameter
Full size table
Fig. 2
figure 2

Probability distribution of collapse pressure at depth 2000 m

Full size image
Fig. 3
figure 3

Probability distribution of fracture pressure at depth 2000 m

Full size image
Fig. 4
figure 4

Collapse and fracture pressure interval with confidence level 90% of XX

Full size image

The conclusion is as follows: the prediction result of collapse and fracture pressure is no longer a single curve or value, but an interval, which is more practical for drilling in complex geological environment. The results of this study are helpful to better describe the collapse and fracture pressure of complex formation and can provide more valuable reference data for drilling design.

Conclusions and recommendations

  1. a.

    In the existing calculation model of collapse and fracture pressure, the input rock mechanical parameters and in-situ stress are all treated according to the fixed value, and the obtained pressure prediction results are all single value results. This method ignores the error between the predicted result and the actual result due to the uncertainty of the input calculation parameters.

  2. b.

    In this paper, the existing calculation model of formation collapse and fracture pressure is established and improved, and the Monte–Carlo simulation method is used to characterize the collapse and fracture pressure, and the uncertainty quantitative description method of formation collapse and fracture pressure is established.

  3. c.

    According to the method established in this paper, the predicted collapse and fracture pressure are no longer a single fixed value curve, but a pressure interval with probability information, which is more practical for drilling in complex geological environment. The results of this study are helpful to better describe the collapse and fracture pressure of complex formation and can provide more valuable reference data for drilling design.