Introduction

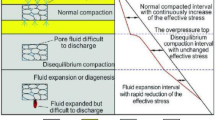
One of the key inputs to successful well planning is accurate pore pressure profile and it is more challenging in frontier areas with complex geology and where few offset wells exist beyond known depths. Such situations have left practitioners with no other option than to adapt existing models for pore pressure prediction work, which in some cases have led to underbalanced drilling with its attendant problems. According to Swarbrick and Osborne (1998), most basins around the world such as the young deltaic shale sequence of Niger Delta are abnormally pressured due to: (1) stress-related mechanisms (tectonism and disequilibrium compaction); (2) fluid expansion due to hydrocarbon generation, mineral transformation, etc.; and (3) fluid movement and buoyancy mechanisms (hydraulic head, osmosis, buoyancy due to density contrasts and lateral transfer).

Traditionally, the method of predicting the pressure of shale-rich rocks is to analyse seismic and well data, working with the principles that (a) high pressure is associated with higher than expected porosity; (b) the parameter used to capture porosity is of good quality with high data density; and (c) the only reason for the overpressure is disequilibrium compaction. The two main relationships used to quantify pore pressure are the (a) Eaton ratio method, an empirical approach in which Eaton provided constants for sonic velocity, resistivity and drilling exponent (Dxc) data, and (b) equivalent depth method, a deterministic approach, which is most commonly used with density and sonic velocity data. Ideally, pore pressure prediction practitioners will use both methods applied to several data types to compare prediction profiles. In that way, a measure of the uncertainty in the prediction can be usefully assessed.

However, the above methods are bound to fail where secondary mechanisms are responsible for generating the overpressure, hence the need for a different model based on velocity–vertical effective relationship (Bower’s 2001), so as to take care of secondary mechanisms that do not conform to the conventional approaches.

Geological setting

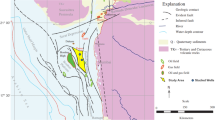
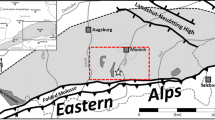
The study area lies within the Northern Delta, Eocene older depobelt (Fig. 1). The three main geological formations that make up the Niger Delta are the Akata, Agbada and Benin formations. But, there exists a variation in the nature and rate of sediment supply and accommodation space resulting in the pattern and nature of sediments deposited in the onshore part of the delta. Most of the thick shales are within the Akata Formation, and this section is the habitat of high overpressures and temperatures observed in the onshore area. This unit is characterised by a near-uniform shale development and probably extends across the whole delta (Short and Stäuble 1967). The age is Eocene to recent but becomes younger towards the sea.

Fig. 1
figure 1

Section map of Nigeria showing the location of study area in the Niger Delta Basin

Full size image

Theory and method

The fundamental theory for pore pressure prediction is based on Terzaghi’s and Biot’s effective stress law (Biot 1941; Terzaghi et al. 1948). This theory indicates that pore pressure in the formation is a function of overburden stress and effective stress. The overburden stress, vertical effective stress and pore pressure can be expressed in the following form:

$$ P_{\text{p}} = \frac{{(S - \sigma_{\text{eff}} )}}{\alpha } $$
(1)

where Pp is the pore pressure; S is the overburden stress; σ eff is the vertical effective stress; and α is the Biot effective stress coefficient. Biot’s coefficient is the ratio of the volume change of the fluid filled porosity to the volume change of the rock when the fluid is free to move out of the rock. It is conventionally assumed α = 1 in many geopressure studies (Zhang, 2011; Azadpour et al. 2015). Bowers (2001), on the other hand, used an empirically determined method to calculate the effective pressure with the following relationship between the effective stress and sonic velocity for disequilibrium compaction setting:

$$ V = V_{0} + A\sigma^{B} $$
(2)

where V is the velocity at a given depth; V 0 is the surface velocity (normally 5000 ft/s); σ is the vertical effective stress; and A and B are the parameters obtained from calibrating regional offset velocity versus effective stress data. In basins with the mechanism of unloading, Bowers proposed the following empirical relation to account for unloading effect:

$$ V = V_{0} + A\left[ {\sigma_{\hbox{max} } \left( {\frac{\sigma }{{\sigma_{\hbox{max} } }}} \right)^{(1/U)} } \right]^{2} $$
(3)
$$ \sigma_{\hbox{max} } = \left( {\frac{{V_{\hbox{max} } - 5000}}{A}} \right)^{1/B} $$
(4)

where U is the unloading parameter which is a measure of how plastic the sediment is. U = 1 implies no permanent deformation and U = ∞ corresponds to completely irreversible deformation. σ max and V max are the values of effective stress and velocity at the onset of unloading which is the maximum. Eaton (1975) introduced (Eq. 5) below is an empirical equation used for pore pressure prediction from sonic transit time:

$$ P_{\text{p}} = S_{\text{v}} - (S_{\text{v}} - P_{\text{hydro}} )\left( {\frac{{\Delta t_{\text{norm}} }}{{\Delta t_{\text{obs}} }}} \right)^{x} $$
(5)

where Pp is the pore pressure, S v is the overburden pressure, Phydro is the hydrostatic pressure, \( \Delta t_{\text{obs}} \) is the observed sonic transit time in shale; \( \Delta t_{\text{norm}} \) is the sonic transit time in shale at the normal pressure condition obtained from normal trend line; and x is the exponent constant which is originally 3 in Eaton’s study, based on data from wells in the shallow coastal areas of the Gulf of Mexico.

This study utilised wireline logs and drilling data from two onshore wells. The data were quality controlled and corrected for any inconsistency. GR cut-off value for shale varies from well to well and can be misleading especially on Onshore Niger Delta; thus, threshold was applied in addition to the GR API range. In this case, sand cut-offs were normally removed from the density log. The generated data are required input to enable proper interpretation and shale pressure estimation.

The cross-plot of Vp versus Rho as modified by Swarbrick (2012) was used to check for secondary mechanism and complimentary to Lahann et al. (2001) plot. These can be used to distinguish overpressures generated by disequilibrium compaction from those generated by unloading mechanisms (Lahann et al. 2001). Normal compaction trend, overburden and hydrostatic pressure gradient were defined for the areas based on geology and fluid density. Eaton’s exponents were obtained by calibrating with the direct pressured measurements and by considering the overall overpressure system of the study area.

Results

The cross-plot of density, velocity vs depth (Fig. 2), shows an increase in sonic velocity (dark blue), relative to bulk density (pink), in the illitized, but not unloaded depth interval. In the unloaded zone, velocity declines dramatically at 12,400 ft TVDml with very little or no change in bulk density (Fig. 2) validating the fact that density can increase even in the zone of unloading.

Fig. 2
figure 2

Identifying secondary overpressure mechanism

Full size image

The analysis from Fig. 3 reveals that shale is hottest (140 °C) at 13,000 ft TVDml (Fig. 3b) and 14,000 ft TVDml, respectively, at constant high density of 2.6 g/cc (cloud of data in pink colour). This could be attributed to interval where the shales are unloading leading to fluid expansion. The onset of this critical interval is approximately at 10,800 ft TVDml and at temperature of 98 °C. This corresponds to the depth interval the deepest kick was recorded (see Fig. 5 inset). Further, at approximately 11,000 ft TVDbml and at temperature of 100 °C, well-A begins to unload (Fig. 3a) giving credence to the fact that unloading could start anywhere shallower in the Northern Delta depobelt. In these plots (Fig. 3a, b), the temperature and pressure increase at burial depth are indicated by the pink and dark red colour in the plots.

Fig. 3
figure 3

a: Velocity–density cross-plot for a well-A based on temperature (left-hand side) and depth (right-hand side). b Well-C based on temperature (left-hand side) and depth (right-hand side)

Full size image

Eaton’s exponent of 3.0 and EDM models is less accurate at this depth interval when compared to mud weight (see Fig. 5) as a proxy to formation pressure (which is usually 500 psi lesser in reality).

It is worth noting that the pressure ramp exceeded a threshold overpressure gradient of 0.7 psi/ft at 12,400 ft TVDml deeper in both wells (Figs. 4, 5) and attesting to the fact that a single method may lead to ambiguity based on the abnormal pore pressure regime and complex geology. A multi-strand approach is most suitable in such situation (Aikulola et al. 2013), and thus, Vp–VES relationship derived for both the loading and unloading scenarios was used to validate the Eaton’s exponents (Figs. 4, 5).

Fig. 4
figure 4

Composite shale pressure profile (blue line) from Bower’s (2001) model compared with other methods (see legend on top left corner) in well-A

Full size image
Fig. 5
figure 5

Composite shale pressure profile (blue line) from Bower’s (2001) model compared with other methods (see legend on top left corner) in well-C

Full size image

Conclusions

The Eaton exponent can be raised in places where disequilibrium compaction is not the only overpressure generating mechanism as indicated by Bowers (2001). For example, Tingay et al. (2009) used exponent of 6.5 in vertically transferred overpressures in Brunei. In central swamp (Middle Miocene) Onshore Niger Delta, Nwozor et al. (2012) used exponent of 6.5, while Chukwuma et al. (2013) raised the exponent to 5 or 6 using data set from Oligocene to Lower Miocene depobelt. In Northern Delta (older) depobelt, Eaton’s exponent ranges of 4.8–5 could be adapted with care for the study area. Otherwise, it would lead to inaccurate estimate of shale pressures at the deeper settings (deeper than 10,000 ft TVDml), especially within the deep shale intervals where secondary mechanism is active and shale temperature is hottest. This is a reflection of different compaction states of the rocks, hence the variation in rock property behaviours which is a function of age, predominant lithology and regional tectonics. The forgoing results show that there is no clear pattern of the distribution of Eaton’s exponent in the study area especially within the hot and deeper settings. Thus, fiddling with the exponent without appropriate geological consideration will lead to pitfalls and partial success of pressure estimates.