Introduction

A main target in the enhanced oil recovery (EOR) process is the economic improvement of the displacement efficiency. The efficiency of the EOR process is controlled by a fundamental factor, known as mobility ratio, which is a function of relative permeability and viscosity of displacing and displaced fluids (Sheng 2011; Sorbie 1991). The main role of injecting water in water flooding process is for the sake of maintaining pressure. Because the viscosity of injected water is often much lower than that of oil, however, it may cause unstable displacement. Increasing the injected water viscosity by addition of a polymer effectively reduces the mobility ratio and results in higher Buckley–Leverett front heights and a more piston-like displacement which ultimately leads to higher recovery efficiency (Sorbie 1991).

In the current polymer flooding process, polyacrylamide polymers with some degree of hydrolysis (HPAM) are the most commonly used polymer (Jung et al. 2013; Sheng 2011). HPAM is formed by replacing some of the acrylamide group in the polyacrylamide polymer with the carboxylic group in the hydrolyzation process. In this synthetic polymer, negative charges have been spread along the chain as a result of presenting the carboxylic group. Eventually, by using this polymer, a chain extension which leads to high solution viscosity is attained due to repulsion between those negative charges.

In fact, in polymer flooding investigations, the precise prediction of the polymer solution viscosity is a critical task. So far, a number of empirical models have been recommended so as to describe the shear rate dependencies of the viscosity of polymeric aqueous solutions, \(\mu \left( {\dot{\gamma }} \right)\). Without a doubt, the power law model is the most utilized model to explain viscosity–shear rate relationship in analytical form. This models also known as the law of Ostwald (Bird and Hassager 1987). The model can be used and employed for both shear thinning and shear thickening behaviors which are given by the following expression (Bird et al. 2007):

$$\mu = k\dot{\gamma }^{n - 1}$$
(1)

where polymer solution viscosity (Pa.s) is shown by μ, index of flow behavior (unitless) is given by n, the flow consistency index (Pa.sn−1) is presented by k, and shear rate parameter (1/s) is shown by \(\dot{\gamma }\). Although Eq. (1) is quite powerful in describing the pseudoplastic region, it fails in predicting observed viscosity behavior at high and low shear rates (Sorbie 1991). According to the previous study (Bird and Hassager 1987; Carreau 1972), the Carreau equation provides a more general model for whole range of shear including low and high shear rates. Here the viscosity function is given by:

$$\mu \left( {\dot{\gamma }} \right) = \mu_{\infty } + \left( {\mu_{o} - \mu_{\infty } } \right)\left[ {1 + \left( {\lambda \dot{\gamma }} \right)^{2} } \right]^{{\left( {n - 1} \right)/2}}$$
(2)

where μ o , μ ∞, λ, n are viscosity at almost zero shear rate, infinite shear rate viscosity, a time constant, and the power law index, respectively.

It has been reported that Carreau equation is more powerful in providing a better fit to the viscosity/shear rate data (Bird and Hassager 1987; Chauveteau 1982); however, compared to the two parameters in power law model, it requires four. This may result in much more complication in a definite analytical calculation which deals with viscosity function (Sheng 2011; Sorbie 1991).

Even though the above-discussed models are powerful in terms of prediction ability, they are only useful for a specific case of reservoir application. To summarize, these models consider the impact of shear rate only while keeping other parameters in a permanent specific value. According to (Levitt and Pope 2008), other process variables, such as brine salinity and polymer concentration, also have a pronounced effect on viscosity of polymer solution.

As an example, the salinity has a significant effect on the viscosity of the polymer solution. The reason is that negative charges along the polymer chain will be screened by the existing monovalent cations in the solution. Then, the screening results in lowering the polymer solution viscosity due to coiling up of polymer chains (Jang et al. 2015; Lee et al. 2009).

One of the other factors with a significant and eminent role is the polymer concentration in the solution. In fact, it has an important role not only in economic matters but also in the determination of the polymer solution viscosity. Overall, a higher solution viscosity will be attained by providing a higher polymer concentration for almost all polymers. This is due to the fact that interaction among the polymer molecules will be increased by adding more polymer into the solution (Rashidi et al. 2010).

The shortcomings of the above-stated models have been recently taken into account by some researchers and have come up with empirical models that can consider the impacts of most process variables (Cheng et al. 2012; Hashmet et al. 2013a, b). For instance, Hashmet et al. (2013a, b) developed an empirical model which is able to predict the viscosity of a polymer solution as a function of different process variables, such as salinity, temperature, degree of hydrolysis. Unfortunately, this empirical model has been developed based on the method of studying the effect of one variable at a time (OVAT). The method of OVAT is a wasteful use of resources and is not capable of identifying the presence of quantifying the interaction among variables. Considering the existence of interaction among the variables, the main effect of one variable on the response is not consistent in the studied range of parameters. In other words, the effect of one variable on the response will be increased or decreased by the level of another variable (Mathews 2005).

By reviewing such a wide range of conditions reported in the previous study, it is clear that in the viscosity modeling of a polymer solution, determination and quantifying individual effects of each input parameter on the viscosity are essential (Sorbie 1991). In developing such a model, the previous study review has indicated that the response surface methodology (RSM) can be a good candidate (Nguyen et al. 2015; Panjalizadeh et al. 2015; Zhu et al. 2015). In this technique in order to develop a regression (empirical) model, a collection of mathematical and statistical techniques is used. And after a specific design of experiment, the goal is defined to minimize an output variable (prediction error) that is affected by several input variables. Runs, a series of tests, are designed in order to carefully asses the response (model output) as a function of changes in input variables. RSM uses a minimal amount of experimental data to develop a model for different industrial processes with high level of accuracy (Box and Wilson 1951). RSM is recognized to model the effect of different input process variables, both main and interaction effects, on the process output variable (Box et al. 2005).

Nowadays, a combination of fuzzy logic and neural network, the so-called neuro-fuzzy technique (FNN) developed by Jang (1993, 1996), Jang and Sun (1995), and Jyh-Shing Roger (1996), has been also employed as a predictive tool in a wide range of disciplines, including engineering. The main reason for using this technique is the accurately finding relationships between the parameters of input and output even for nonlinear functions due to its ability to employ learning algorithms (Aghbelagh et al. 2013; Aïfa et al. 2014; Esmaeilnezhad et al. 2013; Pilkington et al. 2014). Applying fuzzy technique alone has this main drawback that rules should be written by an expert. However, neuro-fuzzy technique as an extension of fuzzy systems has this advantage over fuzzy that input–output relation, in the form of rules, for the presented data, is created automatically. To do so, algorithms of artificial neural networks are utilized to tune system parameters for minimizing the error of the neuro-fuzzy system.

The principal objective of this current study has been to compare the RSM and FNN techniques toward predicting the viscosity of HPAM solutions. A comparison has been performed for both extrapolation purposes and interpolation. The focus of this study is on evaluating the effect of only three input parameters (shear rate, polymer concentration, and salinity) on the viscosity of polymer solution.

The remainders of this paper have been constructed as follows. Firstly, it discusses the experimental work that was carried to extract the data set. The next step is presented in which modeling of the polymer solution viscosity was carried out along with a complete explanation of the procedure. Presented next are the prediction accuracies of the models which were then evaluated using several statistical indices, such as the coefficient of determination (R 2) and root mean square error (RMSE). Analysis of variance (ANOVA) in the matter of RSM was employed to check any significant lack of fit. In the next step, extrapolation capabilities of both developed models, RSM and ANFIS models, were evaluated for unseen data. After performance evaluation of the developed models, the paper ended up with the main conclusions.

Materials and methods

Characterization of HPAM

The commercial polymer used in this study was partially hydrolyzed polyacrylamide (HPAM) with 5 mol. % hydrolysis provided in powder form by SNF Floerger. The polymer had an approximate molecular weight of 8–9 million Daltons (g/mol). Information about degree of hydrolysis and molecular weight was supplied by the manufacturer.

Experimental design

The input parameters of the shear rate (X 1), polymer concentration (X 2), and NaCl concentration (X 3) were investigated for their effects on the polymer solution viscosity. The range of the shear rate, polymer concentration, and NaCl concentration investigation was chosen to be 4–56 (s−1), 700–3300 (ppm), and 2.75–22.25 (g/L), respectively. In fact, these ranges were chosen purposely and the reason is that the polymer solution has a remarkable change in its behavior outside of these ranges. Therefore, this phenomenon was planned to be used to evaluate the accuracy of the developed models in the extrapolation step.

In this current study, a specific design of the RSM, which is called central composite design (CCD), has been employed to determine the experimental conditions because the required complexity of the model was unknown for accurate predictions to be made. Thus, this design allows for a larger range of conditions to be checked compared to other RSM techniques (Box et al. 2005).

An RSM experimental matrix based on three considered factors was generated by using Design Expert (version 7.00) software. The design included 20 runs, consisting of 6 axial points, 8 factorial points, and 6 center points. Table 1 shows experimental conditions of each run, including their coded levels \(\left( { - \alpha = - 1.3, - 1,0,1, \alpha = 1.3} \right)\). The resultant polymer solution viscosity was then modeled using a quadratic equation (Eq. 3):

Table 1 The order and extraction conditions for the central composite design (CCD) including the coded levels of each parameter
Full size table
$$\mu_{\text{pred}} = \beta_{0} + \mathop \sum \limits_{i = 1}^{k} \beta_{i} X_{i} + \mathop \sum \limits_{i = 1}^{k} \beta_{ii} X_{i}^{2} + \mathop \sum \limits_{i < j}^{{}} \mathop \sum \limits_{{}}^{{}} \beta_{ij} X_{i} X_{j} + \varepsilon$$
(3)

where μ pred is the model prediction for the polymer solution viscosity, β 0 is the constant coefficient, β i is linear coefficient, β ii is quadratic, and β ij is interaction coefficient. In this equation, X j and X i are the independent input variables and ε is residual error. In order to meet the assumptions that make the ANOVA valid, the residuals must be normally distributed with a constant variance. The response data were transferred before entering it into the design layout by using the base 10 log.

Neuro-fuzzy

Neural networks and fuzzy logic are naturally complementary implements in constructing intelligent systems. While neural networks are low-level computational structures that are carried out well when dealing with raw data (Jang 1993; Jang and Sun 1995), fuzzy logic handles reasoning on a higher level, using linguistic information provided by field experts (Jang 1996). Nevertheless, fuzzy systems suffer from a lack of learning ability and are not able to regulate themselves to a new condition. Besides, although neural networks are able to learn, they are not clear to the client. Fuzzy logic and neural network are combined together to make a hybrid intelligent system known as a neuro-fuzzy system. Integrated neuro-fuzzy systems can unite with the human-like knowledge representation and clarification abilities of fuzzy systems with the parallel calculation and learning abilities of neural networks (Jang and Sun 1995).

Adaptive neuro-fuzzy inference system (ANFIS)

References (Jang 1993; Jang and Sun 1995) believe that ANFIS is a specific structure in neuro-fuzzy development which has exposed significant outcomes to model nonlinear functions and has been employed for numerous applications in engineering purposes. To add up, ANFIS with its efficient algorithm is able to learn input–output relationship, even with high degree of complexity, and approach any function with a limited number of discontinuities (Silva et al. 2007). ANFIS works in a Takagi–Sugeno-type fuzzy (TSK) inference system, which was extended by Jang (1993, 1996) and Jang and Sun (1995). Fuzzy IF–THEN Sugeno-type rules have been utilized in the rule base of ANFIS. For a first-order two-rule Sugeno fuzzy inference system (Sugeno and Kang 1988), the two rules may be represented by:

  • Fist rule: If x 1 is A 1 and x 2 is B 1 , then y 1  = a 1 x 1  + b 1 x 2  + c 1

  • Second rule: If x 1 is A 2 and x 2 is B 2 , then y 2  = a 1 x 1  + b 1 x 2  + c 1

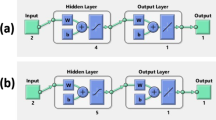
A zero-order TSK fuzzy model will be generated if y 1 and y 2 are constants rather than linear equations. A first-order Sugeno-type FIS, in the form of a relation, is the most accepted inference system used in ANFIS. Antecedent and consequent parameters will be adjusted to equip more accurate outputs with the lowest error during the learning process. By using the ANFIS approach, preceding knowledge of the rule consequent, which is needed in fuzzy systems, is not required because ANFIS finds those parameters during the training process, and consequently adjusts the membership functions. Multilayer feed forward structure of a neural network has an identical structure to ANFIS system, but no weights associated are associated with the links in ANFIS. Figure 1 shows the building of ANFIS, and function of each neuron for each layer is explained below.

Fig. 1
figure 1

Neuro-fuzzy network

Full size image

First layer: Neurons in the input layer, the first layer, just send external crisp signals to the subsequent layer.

Second layer: Neurons in the second layer perform fuzzification.

Third layer: This layer is known as a rule layer. In this step, each neuron corresponds to a single Sugeno-type fuzzy rule. Neurons in this layer compute the firing strength of the rule from fuzzification layer’s outputs (Potter and Negnevitsky 2006). In ANFIS, a product operator is applied to assess the conjunction of the rule antecedents. Therefore, the output of neuron i in Layer 3 is determined as:

$$y_{i}^{(3)} = \mathop \prod \limits_{j = 1}^{k} x_{ji}^{(3)} y_{\prod 1}^{(3)} = \xi_{A1} \times \xi_{B1} = \xi_{1}$$
(4)

where the \(\xi_{I}\) value gives the truth value, the firing strength, of the first rule.

Forth layer: In this layer which is known as normalization layer, each neuron computes the normalized firing strength of a given rule after receiving inputs from all neurons in the rule layer. The normalized firing strength is equal to the ratio of the firing strength of a given rule to the sum of the firing strengths of all the rules. Therefore, the output of neuron i in Layer 4 is obtained as:

$$y_{i}^{\left( 4 \right)} = \frac{{x_{ii}^{\left( 4 \right)} }}{{\mathop \sum \nolimits_{j = 1}^{n} x_{ji}^{\left( 4 \right)} }} = \frac{{\xi_{i} }}{{\mathop \sum \nolimits_{j = 1}^{n} \xi_{j} }} = \bar{\xi }_{i} y_{N1}^{\left( 4 \right)} = \frac{{\xi_{1} }}{{\xi_{1} + \xi_{2} + \xi_{3} + \xi_{4} }} = \bar{\xi }_{1}$$
(5)

Fifth layer: In defuzzification layer, each neuron is linked to a respective normalization neuron and obtains a signal from it. Initial inputs also receive by this neuron. For a given rule, the weighted consequent value is calculated by defuzzification neuron as follows:

$$y_{i}^{(5)} = x_{i}^{(5)} [c_{i0} + a_{i1 } x_{1} + b_{i2} x_{2} ] = \bar{\xi }_{i} [c_{i0} + a_{i1 } x_{1} + b_{i2} x_{2} ]$$
(6)

where \(y_{i}^{(5)}\) and \(x_{i}^{(5)}\) are output and input of the defuzzification neuron i in the layer, respectively, while \(c_{i0}\), \(a_{i1 }\), and \(b_{i2}\) are consequent parameters for rule i.

Sixth layer: This layer is represented by a single summation neuron. The neuron generates the overall ANFIS output, y, after computing the sum of the outputs of all the defuzzification neurons.

$$y = \mathop \sum \limits_{i = 1}^{n} x_{i}^{\left( 6 \right)} = \mathop \sum \limits_{i = 1}^{n} \bar{\xi }_{i} [c_{i0} + a_{i1 } x_{1} + b_{i2} x_{2} ]$$
(7)

ANFIS applied to polymer solution viscosity predicting

The fuzzy inference system structure in this current study was generated from the obtained data using subtractive clustering for modeling of the polymer solution viscosity. In order to implement the ANFIS approach, a type of command line function of MATLAB, ‘genfis2,’ was used and sufficiently trained to find the best ANFIS model. The Gaussian membership function, as a membership function, was utilized in this study for its good performance. This type of ‘genfis2’ does not deliver the same quality of training data results as does test data except that the radii value, a training option parameter, is selected small which may result in over-fitting problems (Jang 1993). To discover the best ANFIS model, having a tolerable error value for both training and test data sets, the training options including radii value must change a great deal to reach a balance point between over-fitting and under-fitting scenarios.

As can be seen in Table 2, the best ANFIS model, by using a sub-clustering structure for this study, was detected based on the ‘gaussian’ membership function type. In this model, we employed ‘mapminmax’ function of MATLAB to normalize the data between −1 and 1. A total of 14 data points (70%) of the experimental data were utilized in training step of the network, while the remaining data are being used for testing. The ANFIS predictions were then applied to produce contour and surface plots in MTALAB software (The Mathworks, Inc., 2013a).

Table 2 Best ANFIS model
Full size table

Experimental procedure

Bulk solution

Sodium chloride (NaCl) solutions of different concentrations ranging from 2.75 to 22.25 (g/l) in water were used as solvents. The temperature here was constant at 24 °C.

Solution preparation

Brine was prepared by dissolving the required weight of NaCl in demineralized water on a mass-balance basis, and it was stirred by using a magnetic stirrer for 15 min. Then, it was stirred at 720 (rpm) until the creation of a vortex was achieved; at the same time, the polymer was added gently to the vortex to avoid agglomeration of the polymer particles. The beaker was covered with an aluminum foil to prevent contact with air. Then, after 30 min, the stirrer speed was decreased to 350 (rpm) and it was further stirred for at least one day to guarantee the complete hydration of the polymer and also to gain a homogeneous polymer solution. Moreover, a standard polymer solution with a concentration of 5000 ppm was prepared. The standard sample was diluted to obtain any desired concentration of polymer in a range from 700 to 3300 ppm.

Viscosity measurement

In order to perform the viscosity measurement, a rotary rheometer, Malvern Bohlin Gemini II, was utilized. The apparent viscosity of prepared polymer solution was measured at 24 °C by changing shear rates from 1 to 100 (s−1) and vice versa. It is noteworthy to mention that no shear rate hysteresis was detected for any of the solutions.

Results and discussion

The result of the RSM model

It should be noticed that coded design variables have been used to perform all of the analysis and model fitting for a CCD and not the design factors in their actual (engineering) units. The reason is that when the engineering units are employed, numerical results will be different and often it will be more difficult to interpret the results in comparison with the coded unit analysis. Moreover, in the coded variable analysis, comparing the effect of changing each design factor over a one-unit interval can be easily achieved by checking the magnitude of the obtained model coefficients (Montgomery 2013). In this study, each independent parameter was coded in five levels (−1.3,−1, 0, 1, and 1.3) as x i according to Eq. (8):

$$x_{i} = \left( {X_{i} - X_{0} } \right)/\Delta X$$
(8)

where X 0 is the value of X i (selected parameters) at the center point and ΔX presents the step change.

Figure 2 shows a scatter plot of the predicted values by the RSM model against the measured experimental data. As evidenced by this figure, majority of the points are located on the line which shows a good agreement between model prediction and experimental data.

Fig. 2
figure 2

Comparison between the polymer solution viscosity predicted by RSM model and the experimentally determined viscosity (response data have been transformed using base 10 log)

Full size image

Table 3 represents coefficient values for the quadratic model for the best fit. The model p_values confirm that all the three design variables had substantial main effects and/or two-factor interactions. Moreover, the quadratic terms were statistically insignificant or marginal except for the polymer concentration quadratic term. Practically, from a higher Fisher’s F test values and lower p_values, a higher significance of each term will be achieved. It can be observed from Table 3 that all of the terms in the developed quadratic model were statistically significant (p_value <0.05) in determining the polymer solution viscosity, and the regression analysis was predominantly linear with respect to the NaCl concentration and shear rate. The quadratic terms that did not show statistical significance were the NaCl concentration*NaCl concentration (p_value = 0.4999) and shear rate*shear rate (p_value = 0.3715). On the other hand, the interaction terms’ p_values (0.005, 0.01, and 007) demonstrate that they had remarkable effects on the polymer solution viscosity and ignoring them would introduce errors into the model prediction outcomes. To judge the goodness of the model fit to the data, the model was also evaluated by examining the lack of fit using ANOVA, with the results shown in Table 4. The relatively small Fisher’s F value and corresponding large probability (p_value = 0.6568) value indicate that there was no evidence of lack of fit in the quadratic model.

Table 3 Regression analysis of the response surface methodology (RSM) model for the viscosity of polymer solution, with the associated statistical significance of each coefficient
Full size table
Table 4 Analysis of variance (ANOVA) to determine the suitability of the developed quadratic model in fitting the experimental data
Full size table

Figure 3 illustrates the process variables effect on the viscosity of polymer solution, while the third variable was kept constant at its specific value (5 g/L, 3000 ppm and 10 s−1). In this type of graph, when the lines are perpendicular to the axes, it means the highest effect for that factor and being parallel to the axes means no effect. As it is shown in Fig. 3a, the polymer concentration in comparison with shear rate had a predominant effect on determining the viscosity of polymer solution. This figure also shows that the influence of shear rate on the viscosity of polymer solution is likely to be increased as the polymer concentration is increased. Furthermore, Fig. 3b indicates that the importance of the NaCl concentration was similar to that of the shear rate on the polymer solution viscosity, suggesting that the NaCl concentration or shear rate could not be increased without significant loss of polymer solution viscosity. Finally, Fig. 3c clearly shows that in comparison with the polymer concentration, increasing the NaCl concentration did not have a significant influence on the polymer solution viscosity. Figure 3 also specifies that the effect of the NaCl concentration on the polymer solution viscosity is likely to be raised as the polymer concentration is increased. Overall, by comparing the slopes of the three different parts in Fig. 3, it was found that the most important parameters affecting the polymer solution viscosity were the polymer concentration, shear rate, and NaCl concentration, respectively, which can also be observed numerically, in Table 3 by checking the associative correlation coefficients.

Fig. 3
figure 3

The influence of input parameters on the viscosity predicted by the RSM model with NaCl concentration held constant at 5 (g/L) (a), polymer concentration held constant at 3000 ppm (b) and with shear rate held constant at 10 s−1 (c)

Full size image

The result of the ANFIS model

In order to model the polymer solution viscosity, we also employed the ANFIS technique. In the absence of a general and precise method to achieve the optimum value of ‘raddi,’ trial and error was the only option. To avoid model prediction from any over-fitting or under-fitting problems, the optimum value of the raddi was specified to be 1.201. Figure 4 shows two scatter plots of the predicted values by the ANFIS model against the measured experimental data for both training and testing data. It is clear that of the testing data, 30% of the raw data file after specifying 70% of the raw data file for training was not applied for the training of ANFIS. The figure clearly shows that the model predicted values were in a very good agreement with the actual data. As the figure shows, almost all the data fell close to the diagonal line which was a confirmation of the model’s accuracy. On the other hand, the coefficient of determination (R 2 = 0.9961) illustrated a good agreement with the two sets of results. The third column of Table 5 shows the viscosity of the polymer solution predicted by ANFIS.

Fig. 4
figure 4

Comparison between the polymer solution viscosities predicted by ANFIS model and the experimentally determined viscosity; training data (a), test data (b). Response data have been transformed using base 10 log

Full size image
Table 5 The experimentally obtained viscosity of polymer solution compared to that predicted by the associated RMS and ANFIS models
Full size table

In order to visualize the relative influence and importance of each input parameter, surface and contour plots have been produced in MATLAB by providing the ANFIS developed model with matrices of the input parameters. Figure 5 demonstrates the results of an investigation generated by the ANFIS developed model. Similar to RSM case, the third variable for each plot was fixed at its specific value (5 g/L, 3000 ppm and 10 s−1). It is obvious that the generated contour plots using the ANFIS model were identical with those from the RMS model. We can observe in Fig. 5a the increase in shear rate from 10 to 50 (s−1) lowered down the polymer solution viscosity and decrease in polymer solution viscosity by reducing the polymer concentration. Similar observations were reported in the previous studies (Akbari et al. 2016; Lewandowska 2007).

Fig. 5
figure 5

Surface plots (left) and corresponding contour plots (right) showing the input parameters on the polymer solution viscosity predicted by the ANFIS model with NaCl concentration held constant at 5 g/L (a), polymer concentration held constant at 3000 ppm (b), shear rate held constant at 10 s −1 (c)

Full size image

Decreasing the apparent viscosity due to shear rate increment demonstrated the behavior of pseudoplastic fluids. The macromolecules orientation along the flow stream line is a good justification for the observed shear thinning behavior of the solution as has been highlighted by different researchers (Ait‐Kadi et al. 1987; Ballard et al. 1988; Carreau 1972; Chagas et al. 2004; Ghannam 1999).

By adding more polymer into the solution for all polymers, interaction among polymer chains will increase and solution states will be changed from dilute region to semi-dilute and concentrated regions which means higher viscosity. Results are in line previous observations (Rashidi et al. 2010; Sorbie 1991). Besides, Fig. 5b shows that viscosity of polymer solutions was reduced by increasing the shear rate and NaCl concentration. These findings also were in line with previous studies (Ait‐Kadi et al. 1987; Chagas et al. 2004; Rashidi et al. 2010). By adding NaCl into the polymer solution, the negative charges distributed along the polymer chain were shielded by Na+ ions and eventually molecules coiled up which led to a lower viscosity for polymer solution (Ait‐Kadi et al. 1987; Chagas et al. 2004; Rashidi et al. 2010). Last but not least, it is projected in Fig. 5c that the higher polymer concentration can be achieved if the polymer and NaCl concentrations set to highest and lowest possible values, respectively.

Comparison of RSM and ANFIS

So as to check prediction ability of the ANFIS and RSM models, their performance was examined by using four well-known statistical measures, namely root mean square error (RMSE), mean absolute percentage error (MAPE), sum of squared errors of prediction (SSE), and the coefficient of determination (R 2), which are defined as follows:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\mu_{\text{pred}} - \mu_{ \exp } } \right)^{2} }$$
(9)
$${\text{MAPE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{\mu_{\text{pred}} - \mu_{ \exp } }}{{\mu_{ \exp } }}} \right| \times 100$$
(10)
$${\text{SSE }} = \, \mathop \sum \limits_{i = 1}^{n} \left( {\mu_{\text{pred}} - \mu_{ \exp } } \right)^{2}$$
(11)
$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\mu_{\text{pred}} - \mu_{ \exp } } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\mu_{\text{pred}} - \left( {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} \;\mu_{ \exp } } \right)} \right)^{2} }}$$
(12)

where μ pred and μ exp are, respectively, forecasted and were observed as the polymer solution viscosity and n is the number of data in the data set. For the RMS model, RMSE, MAPE, and SSE were calculated to be 0.0141, 1.55%, and 0.0040, respectively, while those of the ANFIS model were 0.0142, 1.474%, and 0.004, in order. In addition to the coefficient of determination for both models (R 2 = 0.996 for RSM and R 2 = 0.996 for ANFIS), the similar values for the RMSE, MAPE, and SSE indices confirmed that the models had almost the same superiority in terms of predicting the polymer solution viscosity. It is noteworthy that R 2 and MAPE provided better comparison indices because their values were independent of a unit and remained the same even after data normalization.

Computing residuals, the difference between observation and the predicted values can provide one good index for evaluating the prediction ability of the models. Figure 6 shows that the residuals ranged from −0.46 to 0.42 for the RSM models, while the range was −0.48–0.318 for the proposed ANFIS model. Being associated with almost the same residual ranges, the two developed models had almost the same ability in predicting the polymer solution viscosity.

Fig. 6
figure 6

Residuals of RMS and ANFIS models

Full size image

Developing an ANFIS model may be more complicated than an RSM model. After running experiments based on the designed orthogonal array, and generating a data set, the RSM model was able to be constructed by running a valid regression analysis on the data set. However, the ANFIS model could only be generated by tuning several training options, such as raddi, initial Mu, Mu increase factor, and Mu decrease factor, which was a time-consuming stage. As an example, choosing a small raddi led to an over-fitting problem, which was a good fit for the training data set but a bad fit for the test data, whereas choosing a large raddi value led to an under-fitting problem, which was a poor fitting for both the training and testing data sets. In the absence of a general and precise method to achieve the optimum value of raddi, trial and error was the only option. Finding the optimum value was not a necessity only for the raddi parameter but also for other training option parameters.

It is considerable that the white nature of RSM is still an advantage over the ANFIS nature. Although artificial intelligence systems, including ANFIS, can provide a model for the process with a high degree of accuracy, they cannot be used for study due to their black box nature. In summary, so as to specify the relative importance of each factor on the model response, the implementation of a sensitivity analysis is mandatory, while in the RSM model, the relative importance of each input parameter can be determined simply by looking at the coefficient of each factor in the model equation. Besides that, the interaction among the parameters is not possible to be demonstrated by the ANFIS model even by using a sensitivity analysis, while the RSM model equation shows the existence of interaction not only in a qualitative manner using graphs but also in a quantitative manner. Figure 7, extracted from the RSM methodology results, clearly shows the existence of the interaction among the parameters in a qualitative graph. Lines in interaction plot are not obviously parallel which shows the existence of considerable interaction effect. This is particularly true of interaction for the shear rate*polymer concentration.

Fig. 7
figure 7

Interaction plot for viscosity (data means)

Full size image

Extrapolation evaluation

This part of the study was focused on the extrapolation capabilities of the developed models. For evaluation of the extrapolation abilities of the two developed models, two data sets (500 and 5000 ppm polymer concentrations) lying beyond the originally considered data (700–3300 ppm) were considered. Figure 8 graphically shows the prediction ability of these two models for extrapolation purposes.

Fig. 8
figure 8

Evaluating extrapolation ability of both RSM and ANFIS models in 5 wt% NaCl concentration with different polymer concentration; 5000 ppm (a), 500 ppm (b)

Full size image

The outcomes obtained from the extrapolation step revealed that the models in predicting polymer solution viscosity were not successful. Figure 8a indicates that a good matching for the polymer study with the 5000-ppm concentration has not been achieved with R 2 and MAPE as the quantitative indices were observed to be 0.6 and 21.8% for the RSM and 0.4 and 20.8% ANFIS models, respectively. To be more specific, the evaluation procedure was repeated for the 500-ppm polymer concentration and the results have been demonstrated in Fig. 8(b). Similar to the 5000 ppm, there was a poor matching with R 2 and MAPE values of −7.4849 and 15.5% for RSM and −18.98 and 19.28% for ANFIS being achieved.

The observed results for the RSM model were not far from expectation, but for ANFIS they were. On one side, it is widely accepted by the researchers that RMS, which is a polynomial model, cannot be applied for extrapolation purposes since the approximation is local and restricted to the region of the parameter values (Pilkington et al. 2014). On the other side, a number of researchers have claimed that the ANFIS model is efficient enough to be used for extrapolation purposes (Al-Ghamdi and Taylan 2015) which was certainly not correct here.

In the previous study, two main reasons have been addressed for model prediction failure in extrapolation investigations: the over-fitting problem of the model and unusual behavior of the process outside of the training data set. An over-fitting problem in the RSM model was not observed because of no evidence of lack of fit in the quadratic model (p_value = 0.6568). In addition, for the ANFIS model, good prediction ability for unseen data, presented to the model as test data, confirmed that the model was clear from any over-fitting problem.

Generally speaking, extrapolation in empirical models is valid when the correlational structure detected in the training samples continued outside the samples space. However, as Fig. 9 indicates, the solution viscosity outside of the training range was dissimilar to that inside the training range. On the one hand, the figure shows a considerable increment in the polymer solution viscosity when the shear rate decreased to a nearly zero value for the 5000-ppm polymer concentration. For the 500-ppm polymer concentration, on the other hand, the horizontal line in the data distribution shows that the viscosity of the polymer solution became almost independent of the shear rate. Obviously, these unexpected behaviors were not observed previously in the training data set; hence, this is the main cause of the ANFIS and RSM model failures. Overall, forecasting any response value in a process with drastic changes dealing with an input parameter level falling beyond the originally considered region is expected to have a significantly larger error compared to those which located within the investigated space and have closer values to the input parameters’ average (Al-Ghamdi and Taylan 2015).

Fig. 9
figure 9

Experimental data distribution for viscosity of polymer solution

Full size image

Conclusion

This study has shown that the response surface methodology (RSM) and adaptive neuro-fuzzy inference system (ANFIS) models are successful tools to predict the polymer solution viscosity. So as to evaluate the prediction ability of the developed models, several statistical indices were used. Based on the present study, the following conclusions can be made:

  • A central composite design (CCD), as a specific design of RSM, was chosen to determine the experimental conditions. Regarding the prediction of the polymer solution viscosity in the design ranges, a high coefficient of determination (R 2) value of 99.60% was obtained for the RSM model. This showed the high accuracy of the RSM model.

  • In this study, ANFIS as another approach for modeling has also been considered. The fuzzy inference system structure was generated from the obtained data using subtractive clustering. The Gaussian membership function was used in this study for its good performance. The optimum value of the raddi, one of the main training options, was determined to be 1.201, which led to a reasonable error value for both the training and test data sets and can provide a balance between over-fitting and under-fitting scenarios. Regarding the prediction of the polymer solution viscosity in the design ranges, a high R 2 value of 99.61% was obtained, which showed the high accuracy of the ANFIS model.

  • Generally, it can be concluded that the accuracies of RSM and ANFIS were almost same and they presented interesting results in the design ranges. Besides R 2 values, the root mean square error (RMSE), mean absolute percentage error (MAPE), and sum of squared errors of prediction (SSE) values for each model confirmed that the models have almost the same superiority in terms of predicting the polymer solution viscosity. These results have also been supported by almost the same small residual ranges. The residual range was from −0.46 to 0.42 for the RSM model, whereas the range was from 0.48 to 0.318 for the ANFIS model.

  • Based on to the RSM and ANFIS results, all the independent parameters are not equally important in polymer solution viscosity. The polymer concentration, shear rate, and NaCl concentration are the most important factors in the determination of the polymer solution viscosity, respectively.

  • Extrapolation results showed that although RSM and ANFIS are two powerful tools to be used in design ranges, this does not necessarily mean that they also can be used for extrapolation purposes.

A good match with the actual data was achieved by developing the RSM and ANFIS models. To develop such a model is no need for any human experience or theoretical knowledge during the learning process, which is the main feature of these two models; furthermore, good fitting results have been guaranteed.