Abstract
As unconventional tight oil reservoirs are currently a superior focus on exploration and exploitation throughout the world, studies on production performance analysis of tight oil reservoirs appear to be meaningful. In this paper, on the basis of modern production analysis, a method to estimate dynamic reserve (OOIPSRV) for an individual multistage fractured horizontal well (MFHW) in tight oil reservoir has been proposed. A model using microseismic data has been developed to calculate fracturing network parameters: storativity (ω) and transmissivity ratio (λ). There main focuses of this study are in two aspects: (1) find out effective methods to estimate OOIPSRV for an individual MFHW in tight oil reservoir when there is only production data available and (2) study the relationship between productivity and fracturing network parameters (ω and λ) so as to estimate the productivity for individual MFHW from microseismic data. In order to demonstrate and verify the feasibility of developed methods and models, 5 filed wells and 2 simulated wells have been analyzed. The proposed method to calculate OOIPSRV proves to be applicable for MFHW in tight oil reservoirs. From the calculated results of ω and λ for example wells, it has been found that there exists linear relationship between the value of ω/λ and average production (Q ave) for an individual MFHW completed in this actual tight oil reservoir. On the basis of derived linear relationship between ω/λ and Q ave, the productivity for more individual MFHWs can be directly estimated according to microseismic interpretation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In order to achieve economical exploration, hydraulic fracturing stimulation has been widely used to enhance the production performance of tight reservoirs because of its low or ultra-low permeability (Bello and Wattenbarger 2010). A successful fracturing stimulation can directly improve the deliverability and productivity of an individual well. The significance of production performance analysis is that dynamic reserves and reservoir parameters can be determined.
Often, linear flow is the dominant flow regime in tight reservoirs and production takes place at high drawdowns because of the low permeability. On the basis of linear flow characteristic for MFHW in unconventional reservoirs, modern production analysis method (MPA) has been developed obtain reservoir parameters and perform flow regime identification (Cheng 2011; Song and Ehlig-Economides 2011; Clarkson 2013). Log–log normalized rate versus time plot and square root time plot are two useful tools of MPA to identify flow regime change and obtain characteristic parameters which are available for the estimation of reservoir permeability and effective fracture half length (Clarkson and Beierle 2010; Poe et al. 2012). Ibrahim et al. (2006) derived \(A_{\text{c}} \sqrt {k_{\text{SRV}} }\) and OOIPSRV according to the slope of square root time plot and the end of the linear flow (T elf). A correction factor which corrects the slope of the square root time plot and improves the accuracy of \(A_{\text{c}} \sqrt {k_{\text{SRV}} }\) was presented (Clarkson et al. 2012). OOIPSRV and reservoir parameters could also be calculated from advanced production decline analysis methods (APDA) which is based on the boundary dominated flow regime (Tang et al. 2013). The Arps-Fetkovich-type curves were used to identify the transient versus depleting stages and to estimate the reservoir parameters and future decline paths (Abdelhafidh and Djebbar 2001). A comprehensive presentation of all the methods available for analyzing production data, highlighting the strengths and limitations of each method has been finished (Mattar and Anderson 2003). These methods include Arps, Fetkovich, Blasingame and Agarwal–Gardner (A–G), normalized pressure integrative (NPI) as well as a new method called the Flowing Material Balance. Li et al. (2009) and Qin et al. (2012) performed the production analysis on unconventional gas reservoirs and presented the limitations and the range of application of different curves. As the indexes of fracturing stimulation effectiveness, fracturing network parameters (ω and λ) are widely studied by many scholars. Moghadam et al. (2010) generated dual-porosity-type curves for various Lambda and Omega values, and converted them to a single curve that is equivalent to Wattenbarger’s linear flow-type curve. Al-Ajmi et al. (2003) presented a practical method to estimate the storativity of a layered reservoir with cross-flow from pressure transient data. An estimate of the transmissivity ratio may be obtained from production logs. The storativity on the other hand needs to be determined from the pressure transient data or by independent means (Brown et al. 2011). Lian et al. (2011) derived the collaborative relationship between storativity and transmissivity ratio during the decrease in reservoir pressure. Few works have been done to study the direct relationship between fracturing network parameters (ω and λ) and productivity. However, Sander (1986) proposed a method to estimate the ratio of transmissivity (λ) and storativity (ω) from decline analysis using streamflow data that provides a useful reference when researchers are seeking for the relationship between productivity and fracturing network parameters.
Modern production analysis (MPA) and advanced production decline analysis (APDA) methods are commonly used to evaluate shale gas reservoirs in the previous studies. In this work, we demonstrate the availability of these two approaches in tight oil reservoirs, and we have introduced a solution to estimate OOIPSRV directly on the basis of MPA. As a validation of our introduced method, three APDA techniques (Blasingame A–G and NPI) have been used to calculate OOIPSRV as well. For the purpose of finding out the inside relationship between productivity and fracturing network parameters, a model has been developed to calculate ω and λ for an individual fracturing stage or for the whole MFHW in tight oil reservoir on the basis of microseismic data. Once ω and λ are figured out for an individual MFHW, it becomes easy to find the relationship between productivity and fracturing network parameters. In order to demonstrate the feasibility and applicability of developed methods and models, 5 filed wells and 2 simulated wells have been analyzed. It has been found that there exists linear relationship between ω/λ (the ratio of storativity and transmissivity ratio) and average production of a single MFHW(Q ave) for target tight oil reservoir. On the basis of derived linear relationship, the productivity for more individual MFHW can be directly estimated according to microseismic interpretation. The results of analysis and calculation for actual cases have validated the applicability of proposed solution for OOIPSRV estimation and verified the convenience of developed models for fracturing network parameters calculation. From this study, it provides a method to estimate productivity directly from macroseismic data which is meaningful to be applied to more tight oil reservoirs.
Methodology
MPA is one of the most commonly used methods to conduct production performance for multistage fractured horizontal well (MFHW) completed in unconventional reservoirs. Reservoir parameters and fracture properties can be obtained from production performance analysis using linear flow plot and square root time plot (Clarkson and Beierle 2010; Anderson et al. 2010; Clarkson 2013). Log–log normalized rate vs time plot is use to perform flow regime identification for MFHW in this paper, and a method based on square root time plot analysis to estimate OOIPSRV has been introduced. As modern production performance analysis technique, advanced production decline analysis (APDA) expands the range of application of decline analysis methods. APDA has been applied to carry out reservoir parameters calculation and OOIPSRV evaluation in this study. What’s more, methods to calculate fracturing network parameters (ω and λ) for MFHW according to microseismic interpretation have been developed. With the knowledge of relationship between fracturing network parameters and productivity, it is convenient to estimate the productivity for a new MFHW on the basis of microseismic data.
Modern production analysis method (MPA)
Oil/gas reservoir performance describing methods are based on the high-accuracy pressure data from transient well tests. MPA and well test are the basic facilities which were utilized to evaluate the characteristics and performances of unconventional reservoirs. As for tight oil reservoirs, well test needs very accurate pressure data from transient pressure tests which is time-consuming due to the very low pressure conductivity in tight layers. MPA has been widely adopted to accomplish production performance analysis to obtain useful reservoir parameters and OOIPSRV.
Log–log normalized rate versus time plot analysis
As for MFHW completed in tight oil reservoirs, two dominant flow regimes, transient linear flow regime which may last for several months or years, even several decades and boundary dominated flow, are widely agreed on in this industry. According to previous researches (Clarkson and Beierle 2010) or case studies (Clarkson and Williams-Kovacs 2013; Anderson et al. 2012) for tight oil or shale gas wells, the flow regime identification is performed to determine which model (corresponding to specific flow regime) to be used for reservoir parameters estimation. Many theories and methods have been set up to capture the flow regime changes. In this paper, log–log normalized oil rate versus time plot has been used to identify flow regime. This plot has proven to be useful to perform flow regime identification for fractured horizontal wells completed in tight oil reservoirs (Clarkson 2013; Pinillos and Rong 2015).
During linear flow period, the slope of Log q/(P i − P wf) vs log time plot is equal to −0.5. During the boundary dominated flow, it equals to −1. The most significant contribution of Log–log normalized rate versus time plot in this paper is to identify the linear flow regime and find out the end time of linear flow (T elf) directly. In order to decrease the production data fluctuation led by the change of production systems, the dimensionless rate and dimensionless time have been brought into use in this work, which are defined as follow (Bello and Wattenbarger 2010):
Generate Eqs. (2) and (3) into Eq. (1) (derivation refers to “Appendix 1”):
Equation (4) indicates that there exists linear relationship between normalized pressure and square root time (\(\frac{\Delta p}{q}\) versus \(\sqrt t\)).
Square root time plot analysis
Considering the characteristics of linear flow regimes, we can draw the normalized pressure versus square root of material time plot to figure out the slope (m) of characteristic straight line. Once T elf and m have been determined, the effective permeability (k SRV) and effective fracture half length (X f) of SRV zone can be estimated from Eqs. (5) and (6) (Qin et al. 2012; Chu et al. 2012; Ye et al. 2013).
Linear flow that may last for a long time (several months or years) is the most common flow regime in tight oil reservoirs (Clarkson and Beierle 2010). In order to conform the linear flow, a clear half-slope trend should be observed on the log–log normalized rate and time plot, or a straight line appears on the square root time plot. Note that half-slope trend may not appear on the log–log normalized rates (Anderson et al. 2010), because the skin damage may cover it.
Based on the straight-line behavior of linear flow on the square root time plot, the simplest form of the linear flow equation is (Clarkson et al. 2012):
Considering the interference of adjacent wells, skin factor and finite conductivity, the slope of plot is defined as Eq. (8).
The equations presented above are based on the assumption of a constant flowing pressure. While the flowing pressure of oil well is variable, the slope of square root time plot was given by Anderson et al. (2010):
The product of effective permeability and fracturing half length is as follows:
The slope of characteristic straight line on square root time plot is determined by production performance in substance, and it can be figured out directly from the square root time plot. With the combination of T elf, reservoir parameters (k SRV and X f) and OOIPSRV can be estimated.
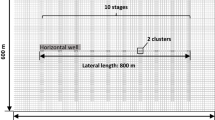
It is assumed that a multistage fractured horizontal well (MFHW) is made up of a series of individual fracture stage, every stages of a MFHW are identical and the number of hydraulic fractures equals the number of fracture stage (Fig. 1). Once the slope of square root time plot (m) is determined, the arithmetic product of total contacted matrix surface areas (A c) for a multistage fractured horizontal well (A c is sum of contacted matrix surface areas for each individual fractures (A c1); every fracture has two contacted surfaces) and effective permeability can be detected from square root time plot analysis (derivation refers to “Appendix 2”):
The right part of Eq. (11) is determined by the slope of square root time plot (m) which is derived from actual production data. Combining with known or measured formation parameters, \(A_{\text{c}} \sqrt {k_{\text{SRV}} }\) is easy to be figured out. Then, the dynamic reserve (OOIPSRV) can also be calculated from Eq. (12). The detailed derivations of Eq. (12) are presented in Appendix 2.
Advanced production decline analysis (APDA)
Many decline analysis curves and models have been established during the history of oil/gas exploration and exploitation. The most typical one is Arps decline curve analysis method which is under the assumption of constant bottom pressure and permeability (Ibrahim et al. 2006). Arps decline curve can only be used to analyze production performance in steady flow regimes. Traditional decline analysis (Arps) gives reasonable answers to many situations except for that it completely ignores the flowing pressure data (Mattar and Anderson 2003). As a result, it may underestimate or overestimate the reserves.
Advanced production decline analysis (APDA) method (including Fetkovich, Blasingame, Agarwal–Gardner, NPI, transient, etc.) breaks the limitations of Arps decline curve, and it can be used to perform the production analysis even if the flow is not steady for a single well (Zhu et al. 2009). APDA can not only be applied to evaluate OOIPSRV, but also be utilized to determine the reservoir parameters (k SRV, r eD et al.). APDA approached to realize the standardization of production analysis curves. Furthermore, it provides a new facility to analyze the storage and drainage characteristics of oil/gas wells qualitatively and quantitatively on the basis of large amount of daily rate and pressure data (Liu et al. 2010).
Type curve matching (TCM) is the main manner to obtain reservoir parameters and OOIPSRV using advanced production decline analysis (APDA). Many scholars and researchers have done a lot of works on APDA and developed many standard charts (Fetkovich 1980; Palacio and Blasingame 1993). In order to decrease calculation error, three kinds of APDA methods (Blasingame, Agarwal–Gardner and NPI) have been adopted to calculate OOIPSRV for MFHWs in this work.
For each kind of TCM, there are three types of curves on the standard chart, namely normalized rate curve, normalized rate integral curve and normalized rate integral derivative curve defined as Eqs. (13), (14) and (15). (Zhu et al. 2009; Liu et al. 2010; Sun 2013).
Normalized rate:
Normalized rate integral:
Normalized rate integral derivative:
As for each kind of APDA method, the steps to perform the production analysis are similar. Due to the fact that the focus of this paper is not to study the differences between different individual APDA methods, not all of the adopted APDA methods have been discussed in detail. Here, we take the Blasingame analysis method as an example to explain how to figure out the OOIPSRV for a MFHW, and for more details about Agarwal-Gardner and NPI methods refer to previous works (Zhu et al. 2009; Liu et al. 2010; Sun 2013). Firstly, the actual production data are used to draw the log normalized rate vs log time curve [log (q/△p] versus log t ca), log normalized rate integration versus log time curve [log (q/△p)i vs log t ca] and log normalized rate integration derivation versus log time curve [log (q/△p)id vs log t ca]. Taking any two of the three types of curves or all of the three curves, a TCM log–log chart is established. Subsequently, the actual TCM log–log chart for target well is applied to fit the developed standard chart to determine the dimensionless borehole radius (r eD). The detailed steps to obtain r eD are presented in “Appendix 3”; once r eD have been figured out, the OOIPSRV and more relevant reservoir parameters can be estimated.
Effective permeability of SRV zone:
Effective wellbore radius (r wa):
The drainage radius (r e) could be calculated from Eq. (16) as r eD and r wa have been obtained:
As shown in “Appendix 3”, we have introduced how to determine the variables which are used to calculate dynamic reserve (OOIPSRV):
Fracturing network parameters calculation
Network fracturing technique is an important method to improve the production for tight oil reservoirs. Fracturing network parameters (ω and λ) are the indexes of fracturing stimulation effectiveness.
Storativity (ω) is defined as the ratio of elastic storage ability of fracture system to the total storage ability of the pay zone. It indicates the relative size of elastic storage ability of fracture system and matrix system (Lian et al. 2011). Resources exchanged between fractures and matrix blocks can be characterized by transmissivity ratio (λ) which reflects how easy or difficult the fluid medium flows into fracture from matrix (Wang 2015).
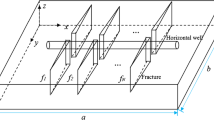
Due to the fact that the main purpose of fracturing stimulation for tight oil reservoir is to develop larger stimulated reservoir volume (SRV), the focus of network fracturing is to connect as many natural fractures as possible based on the shear slide of secondary fracture system. Most proppants are used to support hydraulic fractures, and very few proppants (even if there is some, the proppant size is very small and the volume of those proppants can be ignored comparing the total volume of secondary fractural system in SRV) can be brought into natural fractures. Then, the volume of secondary fracture system can be estimated from the volume of fracturing fluid injected into reservoir layer. Assuming the matrix block is divided into plats by secondary fracture (Fig. 2), the porosity of connected natural fractures is 100% and the system compressibility of secondary fracturing networks is homogeneous, ω and λ are defined as (Warren and Root 1963; Wang 2015):
In conventional natural fractured reservoirs, ω and λ could be detected from pressure buildup testing; however, it is not feasible in tight reservoirs, because it needs too much time to accomplish the pressure buildup test. Thus, we estimate the natural fractures property based on hydraulic fracturing data from microseismic interpretation. The average of original length, width and height of hydraulic fractures are defined as L FO, W FO and H FO separately. The results of microseismic interpretation would provide what we need (L FO, W FO and H FO). The original length, width and height (L FO, W FO and H FO) of hydraulic fractures are detected from microseismic interpretation. The affected length of microseismic events is usually regarded as the original length of hydraulic fractures to calculate ω and λ (Lian et al. 2011; Wang 2015). Due to the fact that the peak of hydraulic fractures may not be effectively supported by proppants, the original fracture length might be much longer than actual supported fracture length (X f derived from square root of time analysis). Likewise, the detected height of microseismic events (H FO) might be larger than the thickness of pay zone (h). The original width of hydraulic fractures (W FO) may be little greater than the supported fracture width according to the size of proppant and the injected amount of sand. Thus, during the calculation of effective stimulated volume for an individual MFHW (effective SRV), we took the calculated effective fracture length of SRV zone (from Eq. 6) as L FO which is based on the actual production performance analysis from MPA. The detected height of microseismic events could be used to determine H FO. If the height is larger than the thickness of pay zone, the thickness of pay zone (h) will be taken as the effective height of SRV zone (H FO). Otherwise, the detected height is going to be regarded as the height of hydraulic fractures. The width of hydraulic fractures was replaced by the supported fracture width which could be estimated according to the size of proppant and the injected amount of sand.
It is assumed that the stimulated reservoir volume (SRV) of an MFHW is a cuboid and the effective well length (l e), original length (L FO) and height (H FO) of fracturing stage detected from microseismic interpretation are regarded as the length, width and height for this stimulated cuboid, and then, the total volume of SRV (V SRV) and hydraulic fractures (V F) are estimated as follow:
Base on the volume and efficiency of fracturing fluid, the volume of secondary fracture system can be calculated:
Volume factor of natural fracture:
In fact, when ω and λ are used to characterize dual-porosity reservoir, secondary fracture network and the original natural fractures are regarded as a unified system (natural fracture system). Network parameters (ω and λ) are determined by the properties of natural fractures (k f,in and R f) in nature. Combining with volume factor of natural fracture, the permeability of natural fractures (k f,in) can be used to characterize the permeability of natural fracture system which is the same as the average permeability of SRV(k SRV). On the contrary, if k SRV has been obtained, the inherent permeability of natural fractures (k f,in) can be estimated. The average permeability of SRV can be figured out from Eq. (5), and then, the inherent permeability of natural fractures (k f,in) can be derived from Eq. (26).
Combining Eqs. (23) to (26), ω and λ are derived (“Appendix 4”):
It is worth to mention that Eqs. (27) and (28) are used to estimate ω and λ for a MFHW as a whole. L FO, W FO, H FO and η are the average values of all fracturing stages for a MFHW. V is the total volume of injected fracturing fluid for the whole well. When calculating ω and λ for an individual fracturing stage (Eqs. 29 and 30), those parameters should be replaced by actual data from microseismic interpretation for a particular fracturing stage (L FOi, W FOi, H FOi and η i). What’s more, not the effective length of horizontal well section (l e) and total volume of injected fracturing fluid for the whole well (V), but fracturing spacing (d = l e/n f) and injected fracturing fluid for a particular fracturing stage (V i) should be used here. Then, ω and λ for each individual fracturing stage is given by:
Example application
In order to demonstrate the application and feasibility of developed methods in detail, 5 field cases from an actual tight oil reservoir have been chosen to carry out the production performance analysis and OOIPSRV evaluation. As a validation, 2 simulated cases have been analyzed as well. In simulated cases, the synthetic data are provided by a semi-analytical productivity prediction model for multistage fractured horizontal wells in naturally fractured reservoirs (Wang et al. 2015; Wang 2015). This productivity model, which can be used to predict the productivity of MFHWs in tight oil reservoirs, is based on the volumetric source methods.
Field cases
As for field cases, 5 MFHWs from an actual tight oil reservoir were chosen to carry out the production performance analysis and OOIPSRV evaluation. The average thickness of reservoir pay zone is about 34.8 m. The porosity is 10% in average, and permeability is about 0.012 mD. The content of clay in the reservoir rock with indistinct sensitivity is low (1.96%). The density of crude oil is 0.89 g/cm3, and the viscosity is 13 mPa s. The pressure system appears to be normal, and pressure coefficient of target oil layers is 1–1.2. Those basic reservoir features and reservoir physical parameters are from reservoir test or well sampling test. In this tight oil reservoir, multistage fracturing stimulation has been performed for every horizontal well to achieve economic development.
Flow regime identification
The characteristics of linear flow after fracturing are the basis of MPA approach. The first step of production performance analysis is to figure out two key parameters (T elf and m) which are essential to the calculation of reservoir parameters and OOIPSRV. Taking Well 1 as an example, we have demonstrated how to identify the flow regimes for a fractured horizontal well completed in tight oil reservoir.
As shown in Fig. 3, the 1/2 slope straight line (blue line) represents linear transient flow regime and the unit slope line (yellow line) characterizes the boundary dominated flow. The production history was divided into two sections by the green vertical line. The flow regime just changed at this intersection point (T elf). We have found that all of the 5 actual wells have reached the boundary dominated flow, and the results of diagnosis are presented in Table 1.
On the square root time plot (Fig. 4), a satisfactory fitting straight line indicates the linear flow regime. The data points begin to deviate from this characteristic straight line at T elf (143th day) that is coincident with Fig. 3. The most significant meaning of this chart is to determine the end time of linear flow (T elf) and the slope of characteristic straight line (m). With knowledge of T elf and m, not only the OOIPSRV can be easily figured out according to Eq. (12), but also the effective permeability of SRV (k SRV) and effective half fracture length (X f) can be estimate from Eqs. (5) and (6), respectively. From Fig. 4, the derived end time of linear flow (T elf) is 143 days and the slope of the square root time plot (m) is 0.17. The calculated OOIPSRV for Well 1 is 102.63 × 104 m3 (Table 1).
Following the analysis steps mentioned above, 5 field examples have been analyzed and the comprehensive calculated results of are shown in Table 1.
Dynamic reserve evaluation
Considering the above flow regimes diagnosis results (as for all of the 5 actual field examples, boundary dominated flow regime have been observed), Blasingame, Agarwal–Gardner (A–G) and normalized pressure integration (NPI) TCM techniques of APDA were utilized to analyze the cases studied in this work. Instead of using a single TCM technique, a collective of TCM approaches were adopted to corroborate the analysis outcomes.
From Figs. 5, 6 and 7, we can see that good fittings of actual production data and standard chart for all 3 kinds of APDA methods (Blasingame, A–G and NPI TCM techniques) have been achieved. On the basis of good fitting of rate data, accurate reservoir parameters and OOIPSRV have been figured out for Well 1 (Table 2). This OOIPSRV determined by the daily oil production and pressure performance only is regarded as the dynamic reserve controlled by Well 1. The main purpose of this section is to find out the OOIPSRV for field wells; not all of the calculation results of reservoir parameters have been presented in this paper.
The final calculation results of OOIPSRV for 5 field examples are shown in Table 3. Comparing Table 3 with Table 1, it is easy to find that the results of OOIPSRV estimation using MPA method are close to the results from APDA.
Calculation of fracturing network parameters
Combining the construction data (injected liquid volume) and microseismic interpretation results (L FOi, W FOi and H FOi), ω and λ of each individual fracturing stage for Well 1 have been calculated (Table 4). From Eqs. (29) and (30), ω and λ of the whole well have been figured out as well (Table 5). As seen from Tables 4 and Table 5, for Well 1, the average values of ω and λ for every individual fracturing stages (ω = 0.003793, λ = 0.001142) are close to the calculated ω and λ of the whole well (ω = 0.003791, λ = 0.001015). In fact, all 5 field examples comply with this fact. Thus, it is convenient and feasible to take the average ω and λ of every individual fracturing stage as the ω and λ for the whole horizontal well. Due to the fact that there are too many calculated data of individual stages for the 5 field wells, to list them all (detailed fracturing network parameters and calculation for Well 1 are shown in Table 4), the calculated ω and λ for all 5 field wells are presented in Figs. 13 and 14.
Simulated cases
In this section, two multistage fractured horizontal well completed in this tight oil reservoir are simulated using a semi-analytical productivity prediction model for multistage fractured horizontal wells in naturally fractured reservoirs (Wang et al. 2015 and Wang 2015). Input reservoir parameters are the average values from this actual tight oil reservoir (Table 6). For these two simulated MFHWs, it is assumed that the number of hydraulic fractures equals the number of stages and all fracturing stages are identical.
The production prediction for 300 days has been carried out using this semi-analytical productivity prediction model. Then, the synthetic data are used to carry out production performance analysis and OOIPSRV estimation as what was done for 5 field examples above.
Flow regime identification
As shown in Fig. 8, the 1/2 slope straight line (blue line) represents linear transient flow regime and the unit slope line (yellow line) characterizes the boundary dominated flow. It indicates that the boundary dominated flow has been observed for this simulated case. From Figs. 8 and 9, the derived end time of linear flow (T elf) is 37 days and the slope of the square root time plot (m) is 0.22. The calculated OOIPSRV for simulated case 1 is 62.29 × 104m3. With the combination of square root time analysis results, reservoir parameters and OOIPSRV have been calculated for those 2 simulated cases (Table 7).
Dynamic reserve evaluation
From Figs. 10, 11 and 12, good fittings of predicted production data with standard chart for all 3 kinds of APDA methods (Blasingame, A–G and NPI TCM techniques) have been achieved. On the basis of good fitting of rate data, reservoir parameters and OOIPSRV have been figured out for 2 simulated cases (Tables 8, 9). Comparing Table 7 with Table 9, it has been found that the results of OOIPSRV estimation using MPA method are close to the results from APDA.
The effectiveness of network fracturing stimulation is positively reflected by ω and λ, and the scale of SRV is the decisive factor of productivity improvement in tight oil reservoirs. Comparing Table 1 with Table 3 (or comparing Table 7 with Table 9 for simulated cases), the OOIPSRV evaluation results from MPA are closed to the outcomes of APDA. It proves to be applicable and accurate when the developed model is used to perform OOIPSRV evaluation in tight oil reservoirs.
With the assumption that the stimulated reservoir volume (SRV) for an MFHW is a cuboid, SRV of field examples and simulated wells have been estimated (Table 10). Taking the effective well length (l e), original length (L FO) and height (H FO) of fracturing stage detected from microseismic interpretation as the length, width and height for this stimulated cuboid, detected SRV from microseismic (DSRV) has been figured. From APDA, SRV for an MFHW can be calculated as well (Table 2). It is certain that this estimated volume can be treated as the effective SRV (ESRV) for an individual MFHW, because oil resource contained in ESRV (dynamic reserve) can potentially be extracted from underground. As shown in Table 10, DSRV and ESRV for 5 field wells have been calculated. Comparing the DSRV from microseismic with ESRV from APDA (Table 10), it has been found that the DSRV is obviously larger than estimated ESRV. It just confirms that the effective SRV is far less than the volume controlled by microseismic events (Wang et al. 2015). It has been found that the effective SRV is about 40.74% of DSRV in average for this tight oil reservoir.
Relationship between fracturing network parameters and productivity
Calculation of ω and λ has been accomplished for 5 field wells completed in tight oil reservoir as mentioned above. After counting the SRV, ω and λ of all the fracture stages for 5 field wells (including Table 4 and more calculated results for other 4 cases), it has been found that there exists exponential relation between fracturing network parameters (ω and λ) and SRV. As shown in Figs. 13 and Fig. 14, there exists apparent exponent relation (Eq. 31) between fracturing network parameters (ω, λ) and SRV, and the relationship parameters are presented in Table 11.
As a statistical result, Eq. (31) reflects the relationship between fracturing network parameters and detected SRV of each individual fracturing stage in this particular tight oil field. Based on Eq. (31), it is applicable to estimate ω and λ for more new wells even if some reservoir parameters are not known because of that SRV can be estimated from microseismic interpretation directly. Certainly, those new wells should belong to the same oilfield block with 5 field wells. It makes sure the relationship between fracturing network parameters and detected SRV complies with this exponent relation. Although Eq. (31) is available for this particular tight oil field, the methods to obtain this equation are applicable for other reservoirs and worth to be promoted. As for a new tight oil reservoir, a new equation (similar to Eq. 31) can be figured out with help of the developed methods, which are used to calculate ω and λ (Eqs. 27–30). Then, ω and λ for more wells in this new tight oil field block can be easily estimated as well.
It is easy to find obvious power relation between ω and λ (Fig. 15). This power function relationship just corroborated that more underground oil resource connected by hydraulic or secondary fractures (higher ω) can be much easily extracted (higher λ) from tight rock whose permeability is ultra-low.
From Fig. 16, on the basis of production performance analysis results, it has been found that there exists dramatic negative linear relationship between the ratio of ω to λ (ω/λ) and the slope of characteristic straight line on square root time plot (m). It is a fact that a smaller m indicates higher productivity for an individual MFHW (From Figs. 4, 9). The average daily production (Q ave), which was collected from metering station for filed wells, and calculated ω/λ are presented in Table 12. As shown in Fig. 17, apparent positive linear relationship between ω/λ and Q ave has been observed. It happens to validate the negative correlation of m and productivity (smaller m implies higher productivity). In other words, for the purpose of improving productivity of a horizontal well in tight oil reservoir, network fracturing techniques should be taken to enhance the storativity firstly. It also means that the key point of fracturing stimulation in tight reservoir is not to establish hydraulic fractures with larger scale but to connect more natural or secondary fractures with hydraulic fractures. This derived linear relationship is not only applicable for 5 field examples but also applicable for 2 simulated wells in this tight oil reservoir (Fig. 17). The consistency of derived relationship (between ω/λ and Q ave) from the analysis field cases and simulated case has just verified the applicability of developed model to calculate ω and λ for MFHW in tight oil reservoirs. The significance of the derived linear relationship between ω/λ and Q ave is that the productivity for more new wells completed in the same oil filed can be estimated approximately according to microseismic interpretation, because ω and λ can be easily estimated (using Eq. 31) on the basis of detected SRV. Indeed, this linear relationship between ω/λ and Q ave (Fig. 17) may be not applicable for other tight oil reservoirs. However, the method developed to calculate network parameters (ω and λ) is worth to be applied to more tight oil reservoir. A new relationship between ω/λ and Q ave could be established for other reservoirs, and then, it is going to be convenient to predict productivity for more MFHWs completed in other tight oil reservoirs.
Conclusions
-
1.
We have developed a model to estimate OOIPSRV and a solution to calculate fracturing network parameters (ω and λ); all the developed models were run for single-phase case. The results of analysis and calculation for 7 cases (5 field cases and 2 simulated cases) have validated the developed models and solutions.
-
2.
Modern production analysis method (MPA) and advanced production decline analysis (APDA) approach are available for production performance analysis of MFHW completed in tight oil reservoirs. Log–log normalized rate vs time plot and square root time plot are convenient methods to perform flow regime identification.
-
3.
It proves to be applicable and accurate when the developed model is used to perform OOIPSRV estimation of individual MFHW completed in tight oil reservoirs due to the fact that the calculated results of OOIPSRV from MPA are closed to the outcomes of APDA.
-
4.
It has been found that there exists exponential relationship between fracturing network parameters (ω and λ) and SRV. Fracturing network parameters (ω and λ) decrease with increase of SRV. Furthermore, the derived exponential relation between fracturing network parameters (ω and λ) and SRV makes it feasible to obtain network parameters for new wells on the basis of SRV estimation.
-
5.
In order to improve the productivity of horizontal tight oil wells, enhancement of ω should be given first priority. Thus, the key point of fracturing stimulation in tight reservoir is not to establish longer hydraulic fractures, but to connect more natural or secondary fractures with hydraulic fractures.
-
6.
For target tight oil reservoir, it has been found that there exists linear relationship between ω/λ and Q ave. On the basis of derived linear relationship between ω/λ and Q ave, the productivity for more individual MFHW can be directly estimated according to microseismic interpretation.
Abbreviations
- A c :
-
Total contacted matrix surface area of hydraulic fracture (m2)
- A c1 :
-
Contacted matrix surface area of hydraulic fractures of a single side (m2)
- \(a,b\) :
-
Relationship factor
- b′:
-
Relationship parameters of square root time plot
- B o :
-
Oil volume factor (m3/m3)
- B oi :
-
Original oil volume factor (m3/m3)
- c t :
-
Total compressibility (MPa−1)
- d :
-
Fracture spacing (m)
- h :
-
Thickness of pay zone layers (m)
- H FO :
-
Average height of every hydraulic fracturing stages (m)
- H FOi :
-
Height of an particular individual fracturing stage (m)
- k SRV :
-
Effective permeability of SRV zone (mD)
- k f,in :
-
Inherent permeability of natural fracture (mD)
- k f :
-
Permeability of hydraulic fracture (mD)
- l e :
-
Eeffective length of the horizontal well (m)
- L FO :
-
Average length of every hydraulic fracturing stages (m)
- L FOi :
-
Length of an particular individual fracturing stage (m)
- m :
-
Slope of square root time plot [MPa/(m3/day day0.5)]
- n f :
-
Numbers of artificial fractures
- N P :
-
Cumulative production (m3)
- OOIPSRV :
-
Dynamic reserve in SRV (m3)
- P i :
-
Initial reservoir pressure (MPa)
- P wf :
-
Bottom hole pressure (MPa)
- ∆p :
-
Drawdown pressure (MPa)
- q :
-
Production rate (m3/day)
- Q ave :
-
Average production of an individual MFHW (m3/day)
- q i :
-
Original production rate (m3/day)
- q D :
-
Dimensionless rate
- q Dd :
-
Dimensionless pseudo-rate
- r e :
-
Drainage radius (m)
- r eD :
-
Dimensionless drainage radius
- R f :
-
Volume factor of natural fracture
- r w :
-
Wellbore radius (m)
- r wa :
-
Effective wellbore radius (m)
- s :
-
Skin factor
- S oi :
-
Original oil saturation (%)
- S wi :
-
Original water saturation (%)
- t :
-
Production time (day)
- T :
-
Reservoir temperature (°C)
- t ca :
-
Material balance time
- t cDd :
-
Dimensionless material balance pseudo-time
- t D :
-
Dimensionless time
- T elf :
-
End time of linear flow (day)
- V :
-
Volume of fracture fluid (104 m3)
- V F :
-
Total volume of hydraulic fractures (104 m3)
- V f :
-
Total volume of natural fracture system (104 m3)
- V SRV :
-
Total volume of SRV zone (104 m3)
- W FO :
-
Average width of every hydraulic fracture (m)
- W FOi :
-
Width of an particular individual hydraulic fracture (m)
- x :
-
SRV of single fracture (106 m3)
- X e :
-
Reservoir width (m)
- X f :
-
Fracture half length (m)
- y :
-
ω or λ
- Y e :
-
Reservoir length (m)
- \(\phi\) :
-
Total porosity of reservoir (%)
- φ m :
-
Porosity of matrix (%)
- μ :
-
Viscosity (mPa s)
- \(\eta\) :
-
Average efficiency of fracturing fluid (%)
- \(\eta_{\text{i}}\) :
-
Efficiency of fracture fluid for a particular individual fracturing stage (%)
- ω :
-
Storativity
- λ :
-
Transmissivity ratio
- A–G:
-
Agarwal–Gardner
- APDA:
-
Advanced production decline analysis approach
- DSRV:
-
Detected SRV from microseismic 104 m3
- ESRV:
-
Effective SRV from advanced production decline analysis 104 m3
- MFHW:
-
Multistage fractured horizontal well
- MPA:
-
Modern production analysis method
- NPI:
-
Normalized pressure integrative
- SRV:
-
Stimulated reservoir volume 104 m3
- TCM:
-
Type curve matching
- d :
-
Derivative
- D :
-
Dimensionless
- f :
-
Fracture
- i :
-
Integration
- id:
-
Integral derivative
- m :
-
Matrix
References
Abdelhafidh F, Djebbar T (2001) Application of Decline-Curve Analysis technique in oil reservoir using a universal fitting equation. In: SPE permian basin oil and gas recovery conference. Society of Petroleum Engineers
Al-Ajmi NM, Kazemi H, Ozkan E (2003) Estimation of storativity ratio in a layered reservoir with crossflow. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Anderson DM, Nobakht M, Moghadam S, Mattar L (2010) Analysis of production data from fractured shale gas wells. In: SPE unconventional gas conference. Society of Petroleum Engineers
Anderson DM, Lian P, Okouma V (2012) Probabilistic for recasting of unconventional resources using rate transient analysis: case studies. In: SPE Americas unconventional resources conference. Society of Petroleum Engineers
Bello RO and Wattenbarger RA (2010) Modelling and analysis of shale gas production with a skin effect. In: SPE annual technical meeting of the petroleum society. Society of Petroleum Engineers
Brown M, Ozkan E, Raghavan R, Kazemi H (2011) Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Cheng YM (2011) Pressure transient characteristics of hydraulically fractured horizontal shale gas wells. In: SPE eastern regional meeting. Society of Petroleum Engineers
Chu L, Ye P, Harmawan I (2012) Characterizing and Simulating the non-stationariness and non-linearity in unconventional oil reservoirs: bakken application. In: SPE Canadian unconventional resources conference. Alberta Society of Petroleum Engineers
Clarkson CR (2013) Production data analysis of unconventional gas wells: Review of theory and best practices. Int J Coal Geo 109–110:101–146
Clarkson CR, Beierle JJ (2010) Integration of microseismic and other post-fracture surveillance with production analysis: a tight gas study. In: SPE unconventional gas conference. Society of Petroleum Engineers
Clarkson CR and Williams-Kovacs (2013) A new method for modeling multi-phase flowback of multi-Fractured horizontal tight oil wells to determine hydraulic fracture properties. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Clarkson CR, Qanbari F, Nobakht M, Heffner L (2012) Incorporating geomechanical and dynamic hydraulic fracture property changes into rate-transient analysis: example from the Haynesville Shale. In: Canadian unconventional resources conference. Society of Petroleum Engineers
Fetkovich MJ (1980) Decline curve analysis using type curves. J Petrol Technol 32(6):1065–1077
Ibrahim M., Suez CU, Wattenbarger RA (2006) Analysis of rate dependence in transient linear flow in tight gas wells. In: Abu Dhabi international petroleum exhibition and conference. Society of Petroleum Engineers
Li Y, Li BZ, Hu YL, Tang ML, Xiao XJ, Zhang FE (2009) Application of modern production decline analysis in the performance analysis of gas condensate reservoirs. Nat Gas Geo 20(2):305–307
Lian PQ, Cheng LS, Li LL, Li Z (2011) The variation law of storativity ratio and interporosity transfer coefficient in fractured reservoirs. Eng Mech 9(28):240–243
Liu XH, Zhou CM, Jiang YD, Yang XF (2010) Theory and application of modern production decline analysis. Gas Ind 30(5):50–54
Mattar L, Anderson DM (2003) A systematic and comprehensive methodology for advanced analysis of production data. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Moghadam S, Mattarand LM, Pooladi-Darvish (2010) Dual Porosity type curves for shale gas reservoirs. In: The Canadian unconventional resources and international petroleum conference. Society of Petroleum Engineers
Palacio JC, Blasingame TA (1993) Decline-curve analysis using type curves: analysis of gas production data. In: SPE joint rocky mountain regional and low permeability reservoirs symposium. Society of Petroleum Engineers
Pinillos C, Rong YC (2015) Integration of pressure transient analysis in reservoir characterization: a case study. In: SPE Asia Pacific oil and gas conference and exhibition. Society of Petroleum Engineers
Poe BD, Vacca H, Benjamin A (2012) Production decline analysis of horizontal well intersecting multiple transverse vertical hydraulic fractures in low-permeability shale reservoirs. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Qin H, Yin L, Chen GR (2012) The application of advanced production decline method analysis in fractured low permeable gas well. Nat Gas Technol Eco 6(3):37–38
Sander JE (1986) The ration, transmissivity/storativity from electric analog values of streamflow. Ground Water 24(2):152–156
Song B, Ehlig-Economides CA (2011) Rate-normalized pressure analysis for determination of shale gas well performance. In: North American unconventional gas conference and exhibition. Society of Petroleum Engineers
Sun HD (2013) Advanced production decline analysis and application. CNKI, Beijinig
Tang R, Li JH, Tao SZ (2013) A brief analysis of several common methods of oil-gas well production decline analysis. Guang Dong Chem Ind 40(264):15–16
Wang JC (2015) Volumetric source model of binary system and its application. Dissertation, Southwest Petroleum University
Wang JC, Li HT, Wang YQ (2015) A new model to predict productivity of multiple-fractured horizontal well in naturally fractured reservoirs. Math Probl Eng 2015:1–9
Warren JE, Root PJ (1963) The behavior of naturally fractured reservoirs. SPE J 3(3):245–255
Ye P, Chu LL, Williams M (2013) Beyond linear analysis in an unconventional oil reservoir. In: Unconventional resources conference-USA. Society of Petroleum Engineers
Zhu YC, Liu JY, Zhang GD, Zhu DL, Li J (2009) Correlation of production decline for gas wells. Nat Gas Exp Dev 32(1):28–31
Acknowledgements
The authors wish to thank State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu for the technical support of this study.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Equations of MPA plot
Dimensionless rate and dimensionless are defined as follow:
Generate Eqs. (34) and (33) into Eq. (32):
Square Eq. (35):
Simplify and inverse Eq. (36)
Take \(\pi\) as 3.14, and take the square root of equation Eq. (37):
Appendix 2: Equations of square root time analysis method
As shown in Fig. 18, there are two sides for an individual hydraulic fracture. The total matrix surface area contacted by a hydraulic fracture (A c) is defined as (Clarkson and Beierle 2010; Clarkson 2013):
Transform Eq. (10) in the body text:
Generate Eq. (39) into Eq. (40):
The total contacted matrix surface area:
There are two sides of an individual fracture. With the assumption that hydraulic fractures of a MFHW are identical and the number of hydraulic fractures equals the number of stage, the contacted matrix surface area for a single side of fracture is (A c1):
From Fig. (12), the volume of SRV for a fractured horizontal well could be calculated approximately:
Combining with Eq. (5):
The oil resource in SRV:
Generate Eq. (47) into (48), the dynamic reserve could be estimated:
Usually, taking the volume factor of oil as a constant, OOIPSRV is estimated as:
Appendix 3: Equations of APDA analysis method
Material balance time, dimensionless material balance time, dimensionless material balance pseudo-time, dimensionless borehole radius and dimensionless pseudo-rate are defined as follow (Palacio and Blasingame 1993; Sun 2013):
The dimensionless borehole radius (r eD) is determined from the fit of production data on standard chart (Fetkovich 1980; Palacio and Blasingame 1993). In standard chart, there are a series of standard curves and each standard curve corresponds to a r eD. On the basis of best fit of production data, the particular standard cure can be detected for a single well, and then, r eD is figured out. It is assumed that all the hydraulic fractures contribute to flow and the individual fractured horizontal well is located in a circular reservoir zone; with the best fit of production data and the knowledge of r eD, reservoir parameters and reserve can be estimated (Liu et al. 2010; Sun 2013).
Selecting an actual data point (t ca, q/△p) arbitrarily from actual production data points, the selected actual production data point (t ca, q/△p) corresponds to a theoretical fitting point on standard chart (tcDa, q Dd). With the combination of detected r eD, the effective permeability (k SRV) and effective borehole radius (r wa) can be calculated:
According to Eq. (54), the controlled radius for a horizontal is:
The total pore volume can be estimated as:
Dynamic reserve in SRV (OOIPSRV):
From previous studies (Liu et al. 2010; Sun 2013), the total pore volume can also be directly estimated from the fitting of production data using arbitrary matched data points:
Then, generate Eq. (61) into Eq. (60), OOIPSRV is:
Appendix 4: Equations of fracturing network parameters
With the combination of Eqs. (20) to (26), the storativity (ω) can be calculated:
And transmissivity ratio (λ):
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Luo, H., Li, H., Zhang, J. et al. Production performance analysis of fractured horizontal well in tight oil reservoir. J Petrol Explor Prod Technol 8, 229–247 (2018). https://doi.org/10.1007/s13202-017-0339-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-017-0339-x