Introduction

Water is an indispensable resource for human beings (Ye et al. 2018). Water scarcity, in turn, can pose significant challenges to the security of energy supplies (Ali and Kumar 2017). Surface water is among Earth’s most important resources (Downing et al. 2021). Several factors such as the loss of trees on a large scale, physical and biogeochemical processes change the hydrologic flow paths and can cause surface water pollution (Mikkelson et al. 2013). In addition, agricultural adaptation to climate changes affects water quality (Fezzi et al. 2017). Pesticide concentrations in surface water occasionally exceed regulated values due to seasonal events or intermittent discharges (Li et al. 2022). Su et al. (2022) studied physical and chemical characteristics of water including Permanganate index, chemical oxygen demand, biochemical oxygen demand (BOD5) using the ingle factor pollution index method and the Nemerow pollution index method and analyzed the temporal and spatial changes of water quality. Yang et al. (2020); Núñez-Delgado et al. (2019); Yan et al. (2021); Weng (2022) investigated water pollution and ways to control it using different methods. Shamshirband et al. (2019) used the ensemble models with the Bates-Granger approach and least square method to develop the multi-wavelet artificial neural network (ANN) models with the aim of studying the proposed models for estimating the chlorophyll concentration and water salinity. They also performed uncertainty analysis to study the efficiency of the proposed neural network models. AlDahoul et al. (2022) used machine learning classifiers such as Extreme gradient boosting, random forest, support vector machine, multi-layer perceptron and k-nearest neighbors to classify suspended sediment load (SSL) in rivers. Tao et al. (2021) presented a plan for models and applications based on artificial intelligence (AI) to model sediment transport in rivers. They also analyzed several related hydrological and environmental aspects. Alizadeh et al. (2018) used water quality parameters such as salinity, temperature and turbidity and flow data to study the river-flow-induced effects on the performance of machine learning models such as artificial neural network, extreme learning machine and support vector regression models to predict water quality. Kouadri et al. (2021) used different artificial intelligence algorithms to calculate the water quality index (WQI) based on the two scenarios of reducing the time consumption and water quality variation in the critical cases.

The transfer and dispersion of pollution in rivers has a significant impact on the environment and agriculture. The classical advection–dispersion equation (ADE) is a parabolic partial differential equation and is obtained from the combination of continuity equation and Fick’s first law (Eq. 1) (Taylor 1954):

$$ \frac{{\partial \left( {AC} \right)}}{\partial t} = - \frac{{\partial \left( {QC} \right)}}{\partial x} + \frac{\partial }{\partial x}\left( {A.D\frac{\partial C}{{\partial x}}} \right) - \lambda .A.C + A.S $$
(1)

where A is the flow area, C is the solute concentration, Q is the volumetric flow rate, D is the dispersion coefficient, λ is the first order decay coefficient, S is the source term, t is the time and x is the distance.

Using the above equation has many complications, including the followings:

  1. 1.

    The dispersion coefficient (D) depends on the fluid characteristics, the hydraulic characteristics of the flow and the river geometry or the shape of the cross-section and the river path.

  2. 2.

    Upstream and downstream boundary conditions are required, for which there are many methods to study and calculate and is time-consuming and expensive in many cases.

  3. 3.

    Considering the water surface changes and the non-prismatic characteristics of the river section, the meshing process in the study river reach will be non-uniform and complex.

  4. 4.

    Data survey of the river cross-sections (A) at appropriate intervals and measuring the flow discharge (Q) is time-consuming and expensive, and with the passage of time the river and the corresponding parameters would change that need to be checked and calculated again.

According to the above explanations, the investigation of river water pollution using the above equation requires a lot of data and is very expensive, time-consuming and complicated. In the present study, a solution is presented with appropriate accuracy to calculate temporal changes in concentration using the linear Muskingum method. The proposed solution does not require flow data, characteristics of river cross-sections and dispersion coefficient, etc., and only need the temporal changes in concentration in the upstream and downstream of the study river reach.

The Muskingum method was first proposed by McCarthy (1938) based on the studies conducted on the Muskingum River, Ohio. In the linear Muskingum method, continuity and storage equations were used as Eqs. (2) and (3):

Continuity:

$$ \frac{dS}{{dt}} \approx \frac{\Delta S}{{\Delta t}} = I - O $$
(2)

Storage:

$$ S = K\left[ {XI + \left( {1 - X} \right)O} \right] $$
(3)

where S is storage, I is inflow, O is outflow, t is time, ΔS = Δt is the rate of storage change during the time interval Δt, K is storage time constant, and X is dimensionless weighting factor that represents the inflow and outflow effects on storage, and ranges between 0 and 0.5 for reservoir storage and 0.3 for stream channels (Mohan 1997). This weighting factor describes the relative importance of inflow and outflow to storage (O’Sullivan et al. 2012).

Yadav and Mathur (2018) The extended VPMM method and SVM and WASVM has been used for flood routing and the results suggest that to predict flood wave movement, the extended VPMM is accurate compared to SVM and WASVM models. Chu and Chang (2009) optimized the parameters in the nonlinear Muskingum method using the PSO algorithm. The comparison between this method and previous ones, including Harmony Search (HS), Linear Regression (LR) and Genetic Algorithm (GA) indicates the higher accuracy and speed of the PSO algorithm in estimating the parameters of the nonlinear Muskingum. Moghaddam et al. (2016) proposed a new four-parameter model for the nonlinear Muskingum method that was used for four flood routings. Norouzi and Bazargan (2020) used the PSO algorithm and two basic floods to optimize the parameters of the linear Muskingum method. Okkan and Kirdemir (2020) They used a combination of PSO with the Levenberg–Marquardt (LM) algorithms to optimize the parameters of the Muskingum method. Wang et al. (2023) used a combination of the mathematical techniques and evolutionary algorithms to develop the Muskingum method. Owing to low computational time, algorithms are very capable of optimizing the parameters of the Muskingum method. Increasing the number of parameters of the Muskingum method will lead to the increased calculation time of algorithm, while the accuracy of results does not change significantly (Farahani et al. 2018).

The use of Advection–dispersion equation (Eq. 1) requires a lot of data such as characteristics of river cross-sections and discharge, upstream and downstream boundary conditions, and the dispersion coefficient in the river. Collecting the mentioned data is very costly and time-consuming, and considering the non-prismatic section of the rivers, the modeling is also complicated. For this reason, in the present study, using the linear Muskingum method and the PSO algorithm, a suitable solution for calculating the temporal changes in the concentration of pollution at different locations was presented. In other words, in previous studies, the temporal changes in discharge (Chow 1959, Vatankhah 2014, Hirpurkar and Ghare 2014, Moghaddam et al. 2016, Bazargan and Norouzi 2018, Norouzi and Bazargan 2020, Norouzi and Bazargan 2021, Bozorg-Haddad et al. 2021) and temporal changes of depth (Norouzi and Bazargan 2022) have been calculated using the linear Muskingum method. However, in the present study, considering the changes in the pollution mass and the continuity equation, an equation was presented to calculate the temporal changes in concentration with appropriate accuracy.

It is worth noting that, in the proposed solution, only the temporal changes in concentration in the upstream and downstream of the study river reach are required.

Materials and methods

Data used

The accuracy of numerical methods can be studied using analytical solutions (Barati Moghaddam et al. 2017). The dissolved material with a concentration of 5 mg/m3 was injected into the flow for a period of 100 min and temporal changes in concentration at distances of 50, 75 and 100 m are shown in Fig. 1 (Barati Moghaddam et al. 2017).

Fig. 1
figure 1

Temporal changes in concentration at different distances

Full size image

The relation between water mass accumulation in the Muskingum method and pollution mass accumulation in rivers

Equation (3) shows the mass of water stored between the upstream and downstream sections in the linear Muskingum method. In the present study, equations were presented for the first time to calculate temporal changes in the concentration of pollution with regard to the pollution mass (M). The mass of pollution in rivers is calculated using Eq. (4).

$$ M = C.Q.\Delta t $$
(4)

According to the continuity equation (Eqs. 2 and 4), the temporal changes of the pollution mass in the steady flow condition are expressed as Eq. (5).

$$ \frac{\Delta M}{{\Delta t}} = \left( {C_{I} - C_{O} } \right)Q $$
(5)

The linear Muskingum equation in flood routing and water mass accumulation study is as Eq. (3), which can be expressed as Eq. (6) in the case of pollution mass accumulation in rivers.

$$ M = K.Q\left[ {X\left( {C_{I} } \right) + \left( {1 - X} \right)C_{O} } \right] $$
(6)

where M is the pollution mass (Kg), CI and CO are the changes in the pollution concentration in the upstream (inlet) and downstream (outlet) sections (Kg/m3), Q is the steady flow discharge (m3/s) and ∆t is the time changes.

Using finite difference method, Eq. (5) is expressed as Eq. (7).

$$ \Delta M = 0.5Q\Delta t\left[ {\left( {C_{I}^{J} + C_{I}^{J + 1} } \right) - \left( {C_{O}^{J} + C_{O}^{J + 1} } \right)} \right] $$
(7)

According to the continuity, Eq. (6) is expressed as Eq. (8).

$$ \Delta M = K.Q\left[ {X\left( {C_{I}^{J + 1} - C_{I}^{J} } \right) + \left( {1 - X} \right)\left( {C_{O}^{J + 1} - C_{O}^{J} } \right)} \right] $$
(8)

where CJ and CJ+1 are the concentration at t and t + 1, respectively.

By equating Eqs. (7), (8), and (9) is obtained.

$$ C_{O}^{J + 1} = H_{1} \,C_{I}^{J + 1} + H_{2} \,C_{I}^{J} + H_{3} \,C_{O}^{J} $$
(9)

where H1, H2 and H3 are given as:

$$ H_{1} = \frac{0.5\Delta t - KX}{{K - KX + 0.5\Delta t}} $$
(10)
$$ H_{2} = \frac{0.5\Delta t + KX}{{K - KX + 0.5\Delta t}} $$
(11)
$$ H_{3} = \frac{K - KX - 0.5\Delta t}{{K - KX + 0.5\Delta t}} $$
(12)

The above equations which are presented for the first time in the present study indicate that the equations of the linear Muskingum method for calculating temporal changes in concentration are exactly equal to the equations for calculating temporal changes in flow discharge. In other words, if the temporal changes in pollution concentration at the inlet and outlet of the study river reach are known, the parameters of the linear Muskingum method (X, K, ∆t) and consequently, the temporal changes in pollution concentration in the downstream of the study river reach can be calculated. Using the obtained parameters in the Muskingum method, the temporal changes in concentration of any other pollution in the same river reach can be calculated.

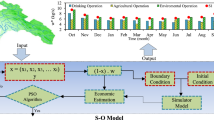
Particle swarm optimization algorithm (PSO) has been used in water quality management (Afshar et al. 2011; Lu et al. 2002; Chau 2005), the linear Muskingum method (Chu and Chang 2009; Norouzi and Bazargan 2021, 2022) and porous media hydraulics (Norouzi et al. 2022a, 2022b). In other words, the efficiency and speed of the mentioned algorithm have been proven in previous studies, and for this reason, in the present study, the PSO algorithm with objective function Eq. (13) and presented flowchart in Fig. 2 was used to optimize the parameters of the Muskingum method.

$$ MRE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{C_{i} - c_{i} }}{{C_{i} }}} \right|} *100 $$
(13)

where Ci and ci are the calculated and observed concentrations in the downstream, respectively and n is the number of data.

Fig. 2
figure 2

Flowchart of the particle swarm optimization (PSO) algorithm

Full size image

Results and discussion

In general, the present study includes the followings:

  1. 1.

    Using the linear Muskingum method equations in flood routing and determining the changes in the mass of pollution instead of the volume of stored water, an equation was presented to calculate the temporal changes in the concentration of pollution, which is highly accurate and efficient. It is worth noting that the proposed solution is much simpler than advection–dispersion equations and requires much less data.

  2. 2.

    The temporal changes in the input and output concentrations, the mentioned equations and the PSO algorithm were used to optimize constant values of the parameters (X, K, ∆t). In other words, all the data related to the changes in the concentrations in the upstream and downstream have been used to calculate the mentioned parameters.

  3. 3.

    The input concentration in the beginning area is greater than the output concentration, the input and output concentrations are maximum in the peak area, and the output concentration is greater than the input concentration in the end area. In addition, the parameters (X, K, ∆t) are also a function of the input and output concentrations. For this reason, to increase the accuracy and efficiency of the solution presented in the present study, three different values for the mentioned parameters were optimized using the PSO algorithm. In other words, the temporal changes in the input concentration were divided into three parts for which different values were optimized and used in calculations.

In order to study the pollution in the rivers using the advection–dispersion equations (Eq. 1) a lot of data are required including river cross-section characteristics in the study river reach at appropriate intervals, dispersion coefficient (D), and upstream and downstream boundary conditions, etc., which is very expensive and time-consuming. However, the linear Muskingum method only requires temporal changes of concentration in the upstream and downstream, and for this reason, it is very low cost. In previous studies, the Muskingum method was used for flood routing. However, in the present study, instead of using the stored volume of water in the Muskingum equation (Eq. 3), the pollution mass (M) in the steady flow condition is used, according to Eq. (6). In other words, the temporal changes of concentration in spatial distances (Upstream and Downstream) are similar to the temporal changes of discharge during floods, and for this reason, the linear Muskingum method is also suitably efficient and accurate in pollution routing. The calculated temporal changes in concentration considering an upstream point of X = 50m and downstream points of X = 75m and X = 100m, an upstream point of X = 75m and a downstream point of X = 100m are shown in Fig. (3). In addition, the parameters (X, K, ∆t) in different conditions and the total MRE, MRE of the peak area and the relative error of the peak concentration (DPO) are listed in Table 1.

Table 1 Parameters of the linear Muskingum method considering constant parameters and errors
Full size table

If instead of using a constant value for the parameters (X, K, ∆t), three different values are used for the starting, peak and ending areas, the accuracy of the Muskingum method in calculating the output hydrograph is increased (Bazargan and Norouzi 2018). For this reason, in the present study, three different values were used for the mentioned parameters, and the accuracy of the calculations in estimating the temporal changes in concentration (Fig. 3) increased. The values of the mentioned parameters in different cases and the values of total MRE, MRE of the peak area and DPO are listed in Table 2.

Fig. 3
figure 3figure 3

Temporal changes of concentration in different conditions

Full size image
Table 2 Parameters of the linear Muskingum method considering different parameters and errors
Full size table

Estimating the peak pollution concentration is very important. According to Table 2, the use of three different values for the parameters of the linear Muskingum method (X, K, ∆t) is more accurate in comparison to using a constant value for the mentioned parameters. In other words, the DPO value in the case of using three different parameters and a constant parameter for X = 50 m (Up) and X = 75m (Down) was equal to 1.28 and 2.34%, respectively, for X = 50 m (Up)) and X = 100 m (Down) was equal to 1.46 and 6.69%, respectively, and for X = 75 m (Up) and X = 100 m (Down) was equal to 1.87 and 5.42%, respectively.

In other words, the results presented in Fig. 3 and Tables 1 and 2 indicate that according to the changes in the concentration of pollution in the three areas of the beginning, peak and end, and since the parameters of the linear Muskingum method (X, K, ∆t) are also a function of the pollution concentration, the use of three different values for the mentioned parameters increased the accuracy of the proposed solution in estimating the output concentration.

Conclusions

Investigating pollution and how it is transferred and its prediction is very important in water engineering and environmental engineering. To study the temporal changes in the concentration using the advection–dispersion equations, a lot of data are required including the characteristics of river cross-sections at appropriate intervals, dispersion coefficient (D), upstream and downstream boundary conditions, etc., and is therefore very expensive and time-consuming. In the present study, the pollution mass (M) was used for the first time instead of the stored water volume (S) in the linear Muskingum method and highly accurate and efficient equations were presented to calculate temporal changes in the concentration. The proposed equation only requires the temporal changes of concentration in the upstream and downstream of the study river reach (far less than that of the advection-transfer equations) and consequently, requires less cost in the process of analysis and calculations. It is worth noting that in previous studies, the linear Muskingum method was used to calculate the temporal changes in discharge and flow depth.

The results of the present study include the followings:

  1. 1.

    Total Mean relative (MRE), peak area and DPO errors in the case of using different parameters (X, K, ∆t) for x = 50 m (Up) and x = 75 m (Down) were equal to 6.52, 0.59 and 1.28 percent, respectively, for x = 50 m (Up) and x = 100 m (Down) were equal to 2.34, 0.95 and 1.46 percent, respectively, and for x = 75 m (Up) and x = 100 m (Down) were equal to 5.57, 1.53 and 1.87 percent, respectively.

  2. 2.

    If the Muskingum method and constant parameters are used in calculation of the temporal changes in concentration, the mentioned values are equal to 7.08, 1.02 and 2.34%, 7.41, 11.06 and 6.69% and 6.75, 3.59 and 5.42%, respectively.

In other words, the proposed solution has a good accuracy in calculating temporal changes in concentration, and if instead of using constant parameters, three different values are used for the mentioned parameters, the accuracy of the calculations is increased.

The proposed method can be used by researchers in the fields related to water pollution and environment. In future studies, other hydrological routing methods and other algorithms can be used to study the temporal changes in the concentration.