Adsorption and biodegradation of 2-chlorophenol by mixed culture using activated carbon as a supporting medium-reactor performance and model verification

Abstract

A non-steady-state mathematical model system for the kinetics of adsorption and biodegradation of 2-chlorophenol (2-CP) by attached and suspended biomass on activated carbon process was derived. The mechanisms in the model system included 2-CP adsorption by activated carbon, 2-CP mass transport diffusion in biofilm, and biodegradation by attached and suspended biomass. Batch kinetic tests were performed to determine surface diffusivity of 2-CP, adsorption parameters for 2-CP, and biokinetic parameters of biomass. Experiments were conducted using a biological activated carbon (BAC) reactor system with high recycled rate to approximate a completely mixed flow reactor for model verification. Concentration profiles of 2-CP by model predictions indicated that biofilm bioregenerated the activated carbon by lowering the 2-CP concentration at the biofilm-activated carbon interface as the biofilm grew thicker. The removal efficiency of 2-CP by biomass was approximately 98.5% when 2-CP concentration in the influent was around 190.5 mg L⁻¹ at a steady-state condition. The concentration of suspended biomass reached up to about 25.3 mg L⁻¹ while the thickness of attached biomass was estimated to be 636 μm at a steady-state condition by model prediction. The experimental results agree closely with the results of the model predictions.

Introduction

Chlorophenols are xenobiotic contaminants that occur during numerous anthropogenic activities and become released into the environment (Zilouei et al. 2006). These compounds are widely used as mothproofing agents, miticides, germicides, algicides, fungicides, and wood preservatives as well as for the synthesis of dyes and drugs (Arora and Bae 2014). Owing to their biocide properties, chlorophenols in industrial wastewater pose serious ecological problems as environmental pollutants (Salmerón-Alcocer et al. 2007; Bajaj et al. 2008). Because of their ecological risk, chlorophenols become the target of investigations focusing on their possible biodegradation (Khodadoust et al. 1997; Wilson et al. 1997). Various chlorophenols, including 2-chlorophenol (2-CP), have been listed as priority pollutants by US Environmental Protection (EPA) (Oh et al. 2011). Fortunately, these compounds can be degraded by indigenous microorganisms under aerobic and anaerobic conditions (Häggblom et al. 2000). In aerobic pathway, the biodegradation of chlorophenols is more diverse since the ring cleavage may occur before dechlorination, thus forming more complex intermediates of various toxicity (Chang et al. 2003). Contrarily, many types of microorganisms, Desulfomonile tiedjei, Desulfitobacterium chlororespirans, and Desulfitobacterium dehalogenans, are known to utilize chlorophenols as their sole carbon and energy source under anaerobic conditions. The anaerobic pathway produced less-chlorinated intermediates that are less toxic to the environment (Bajaj et al. 2008; Chang et al. 2003). For large scale wastewater treatment, mixed consortia rather than pure cultures are preferred because they are easier to handle and contain diverse microorganisms capable of withstanding various unfavorable influent fluctuations.

Traditional technologies based on adsorption, frequently involving the used of activated carbon, are easily applicable processes for the removal of toxic organic pollutants in wastewater. Although activated carbons are found to be fairly effective in extracting organic pollutants from wastewater, however, a significant fraction of the adsorbent is lost cycle by cycle or may be destabilized mechanically in their rather expensive regeneration process (e.g. thermal desorption) (Ilisz et al. 2002). Additionally, activated carbon rapidly loses its adsorptive capacity due to non-selective adsorption for almost all organic contaminants present in wastewater (Aktaş and Çeçen 2007). Accordingly, economic reasons explain why the development of bioregeneration of activated carbon is attracting increasing interest. Desorption of the biodegradable compounds will lead to bioregeneration and a renewal of the adsorption capacity of activated carbon (Ng et al. 2010). Simultaneous adsorption and biodegradation has been proven to be biologically regenerated activated carbon through various mechanisms, thus prolonging its service period (Lee and Lim 2005). In this viewpoint, the application of biological activated carbon (BAC) appears to be a better alternative to conventional treatment technologies. The BAC process provides several potential advantages including surface roughness which enhances biofilm attachment and development, and high surface area which sustains a large amount of biofilm.

Kinetic models are of value in investigating both the capacity and stability of biological processes which utilize inhibitory substrates. In this study, a kinetic model based on the Haldane equation was developed to simulate both adsorption and biodegradation quantities of a biological activated carbon (BAC) column under a non-steady-state condition, so as to predict the effluent concentrations of 2-CP and suspended biomass, biofilm growth, fluxes into activated carbon and biofilm and concentration profiles of 2-CP in the activated carbon, biofilm and diffusion layer. Experimental data were used to verify the kinetic model in fitting measured values of biokinetic parameters obtained from the batch kinetic tests. The experimental and modeling results obtained from this study are expected to demonstrate feasible operation strategies to utilize the BAC process for an efficient adsorption and biodegradation of chlorophenol-laden wastewaters.

Kinetic model system

Conceptual basis and model assumptions

Figure 1 presents the hypothetical concentration profiles for single granular activated carbon (GAC) particles during bioregeneration (Speitel et al. 1987). The kinetic BAC model includes consideration of processes occurring in the liquid surrounding the GAC particles, in the biofilm attached to the GAC and within the GAC particles. The basic assumptions of kinetic model are that (1) the granules used in the BAC are spherical in shape, and the biofilm is homogeneous and the density of the biofilm is constant; (2) biodegradation may occur both bulk liquid and biofilm phases, but does not occur in the pores of granules, because the size of most meso- micro-pores (<0.05 µm) of GAC is less than the size of a microbe; (3) the biological activity is assumed to be substrate-limiting and its kinetics are presented by Haldane model; (4) adsorption is completely reversible; (5) local equilibrium between the surface concentration and liquid concentration that occurred at the biofilm-carbon interface was best described by Freundlich isotherm model; (6) increase in biofilm thickness is due to the growth of biofilm because attachment of biomass from bulk liquid phase is negligible; (7) biomass lost from the surface of activated carbon due to flow shear was directly transferred to bulk liquid phase to form suspended biomass; (8) surface diffusion is initially considered in modeling solute transport into GAC; and (9) 2-CP concentration at any point in bulk liquid phase is the same due to complete mixing by high recycle flow rate.

Fig. 1

Hypothetical concentration profiles for single GAC particles during bioregeneration

Intraparticle diffusion

Surface diffusion is the major intraparticle transport mechanism. The homogeneous solid surface diffusion model for GAC and the initial condition are expressed as follows (Speitel et al. 1987; Smith and Ghiassi 2006):

$$\frac{\partial q}{\partial t} = \frac{{D_{\text{ef}} }}{{r_{\text{f}}^{2} }}\frac{\partial }{{\partial r_{\text{f}} }}\left( {r_{\text{f}}^{2} \frac{\partial q}{{\partial r_{\text{f}} }}} \right),\quad 0 \le r_{\text{f}} \le R_{\text{a}}$$

(1)

$${\text{IC}}:q = 0,\quad 0 \le r_{\text{f}} \le R_{\text{a}} ,\;\;t \ge 0$$

(2)

In the above equation, q is the surface concentration of adsorbed 2-CP (M_s M ⁻¹_q ); D _ef is the surface diffusivity (L² T⁻¹); r _f is the radial coordinate in activated carbon (L); and t is time (T). Two boundary conditions are required for this parabolic partial differential equation to be a well-defined model system which can be solved numerically. The concentration profile is symmetric with respect to the center of the carbon particle; thus

$${\text{BC1}}:\frac{\partial q}{{\partial r_{\text{f}} }} = 0\quad r_{\text{f}} = 0,\;\;t \;\ge \;0$$

(3)

The other boundary condition can be found at the biofilm–carbon interface. The rate of 2-CP transport through biofilm–carbon interface must exactly balance the rate of change in the amount of adsorbed 2-CP in the activated carbon, and this relation can be described as follows (Speitel et al. 1987; Tsai et al. 2005):

$${\text{BC2}}:D_{\text{f}} \frac{{\partial S_{\text{f}} }}{{\partial z_{\text{f}} }} = \frac{{\rho_{\text{a}} }}{{R_{{^{\text{a}} }}^{ 2} }}\frac{\partial }{\partial t}\int_{0}^{R} {qr_{\text{f}}^{2} {\text{d}}r_{\text{f}} } ,\quad r_{\text{f}} = R_{\text{a}} ,\;t\; \ge\; 0,$$

(4)

where R _a is the radius of activated carbon particle (L); S _f is the 2-CP concentration in the biofilm (M_s L⁻³); D _f is the 2-CP diffusion coefficient in the biofilm (L² T⁻¹); z _f is the radial coordinate in the biofilm (L); and ρ _a is the apparent activated carbon density (M_q L⁻³).

The Freundlich adsorption equilibrium relationship applied at the biofilm–carbon interface is described as follows (Sirotkin et al. 2001):

$${\text{BC 3}}:q_{\text{p}} = K_{\text{p}} S_{\text{p}}^{1/n} ,\quad r_{\text{f}} = R_{\text{a}} ,\;t \ge 0,$$

(5)

where q _p is the surface concentration of 2-CP at the biofilm-activated carbon interface (M_s M ⁻¹_q ); S _p is the 2-CP liquid concentration of at the biofilm-activated carbon interface (M_s L⁻³); and K _p and 1/n are the Freundlich isotherm coefficients.

Diffusion with biodegradation in biofilm

Assuming that 2-CP concentration within the biofilm changes only in the z _f-direction normal to the surface of the biofilm, the utilization rate in the biofilm based on diffusion (Fick’s law) with biological inhibition reaction (Haldane kinetics) and initial condition can be expressed as (Jih and Huang 1994):

$$\frac{{\partial S_{\text{f}} }}{\partial t} = D_{f} \frac{{\partial^{2} S_{\text{f}} }}{{\partial z_{\text{f}}^{2} }} - \frac{{kS_{\text{f}} }}{{K_{\text{s}} + S_{\text{f}} + \frac{{S_{\text{f}}^{2} }}{{K_{\text{i}} }}}}X_{\text{f}} ,\quad 0 \le z_{\text{f}} \le L_{\text{f}} ,\;t \ge 0$$

(6)

$${\text{IC}}:S_{\text{f}} = 0,\quad 0 \le z_{\text{f}} \le L_{\text{f}} ,\;t = 0$$

(7)

In the above equations, S _f is the concentration of 2-CP in the biofilm (M_s L⁻³); D _f is the diffusion coefficient of 2-CP in the biofilm (L² T⁻¹); k is the maximum specific utilization rate of 2-CP (M_s M_x T⁻¹); K _s is the Monod half-velocity coefficient of 2-CP (M_s L⁻³); K _i is inhibition constant for 2-CP (M_s L⁻³); and X _f is the density of biofilm (M_x L⁻³). Two boundary conditions are required for Eq. (6). Since the biofilm shares one boundary condition with activated carbon, the boundary condition at the biofilm–carbon interface in Eq. (4) must also be satisfied for Eq. (6). It must also be noted that at the liquid–biofilm interface, the flux across the interface from the liquid phase must be balanced by the flux across the interface into biofilm so that the second boundary equation can be expressed as follows (Tsai et al. 2005):

$$\left. {{\text{BC2}}:D_{f} \frac{{\partial S_{\text{f}} }}{{\partial z_{\text{f}} }}} \right|_{{z_{\text{f}} = L_{\text{f}} }} = k_{\text{f}} \left( {S_{\text{b}} - S_{\text{s}} } \right),\quad t \ge 0$$

(8)

Growth of biofilm

As the 2-CP diffuses into and through the biofilm during biodegradation, the biofilm utilizes 2-CP as carbon source for biosynthesis and respiration. The biomass in the biofilm can increase or decrease with time until the growth rate is balanced by the decay rate and shear loss rate. Since the density of biofilm is assumed constant, the volume of biofilm and thus the thickness of biofilm must increase with time as the biofilm grows. Therefore, the 2-CP diffuses through a boundary which can be moving with time. The boundary is liquid–biofilm interface. Since the biofilm grows upon the utilization of 2-CP, the growth rate of biofilm and initial condition can be expressed by the following equation:

$$\frac{{{\text{d}}L_{\text{f}} }}{{{\text{d}}t}} = \int_{0}^{{L_{\text{f}} }} {\left( {\frac{{YkS_{\text{f}} }}{{K_{\text{s}} + S_{\text{f}} + \frac{{S_{\text{f}}^{ 2} }}{{K_{\text{i}} }}}} - b - b_{\text{s}} } \right){\text{d}}z_{\text{f}} } ,\quad 0 \le z_{\text{f}} \le L_{\text{f}} ,\;t \ge 0$$

(9)

$${\text{IC}}:L_{f} = L{}_{f0}\quad t = 0,$$

(10)

where L _f is the biofilm thickness (L); Y is the growth yield of biomass (M_x M  ⁻¹_s ); b is the decay rate of biomass (T⁻¹); and b _s is the shear-loss coefficient of biofilm (T⁻¹). The initial biofilm thickness must be set to a small value in order that the biofilm can start grow for model prediction.

Mass balances of 2-CP and suspended biomass

A fixed biofilm reactor in which the kinetic model can be applied is a completely mixed biofilm reactor. All suspended biomasses at the liquid–biofilm interface are exposed to the same 2-CP concentration. Since the reactor is operated at a high recycle flow rate and the recycle system can be considered as a part of control volume, the mass balance of 2-CP and suspended biomass in the bulk liquid as well as initial conditions can be described by the following equations:

$$\frac{{{\text{d}}S_{\text{b}} }}{{{\text{d}}t}} = \frac{Q}{V\varepsilon }\left( {S_{{{\text{b}}0}} - S_{\text{b}} } \right) - k_{\text{f}} \left( {S_{\text{b}} - S_{\text{s}} } \right)\frac{{3X_{\text{w}} \left( {R_{\text{a}} + L_{\text{f}} } \right)^{3} }}{{V\varepsilon \rho_{\text{a}} R_{\text{a}}^{3} }} - \frac{{kS_{\text{b}} }}{{\left( {K_{\text{s}} + S_{\text{b}} + \frac{{S_{\text{b}}^{2} }}{{K_{\text{i}} }}} \right)}}X_{\text{b}} ,\quad t \ge 0$$

(11)

$$\frac{{{\text{d}}X_{\text{b}} }}{{{\text{d}}t}} = \left( {\frac{{YkS_{\text{b}} }}{{K_{\text{s}} + S_{\text{b}} + \frac{{S_{\text{b}}^{2} }}{{K_{\text{i}} }}}} - b - \frac{Q}{V\varepsilon }} \right)X_{\text{b}} + \frac{{3X_{\text{w}} b_{\text{s}} L_{\text{f}} X_{\text{f}} }}{{V\varepsilon \rho_{\text{a}} R_{\text{a}} }},\quad t \ge 0$$

(12)

$${\text{IC1}}:S_{\text{b}} = 0,\quad t = 0$$

(13)

$${\text{IC2}}:X_{\text{b}} = X_{{{\text{b}}0}} ,\quad t = 0,$$

(14)

where S _b is the concentration of 2-CP in the bulk liquid (M_s L⁻³); S _b0 is the concentration of 2-CP in the feed (M_s L⁻³); S _s = concentration of 2-CP at liquid-biofilm interface (M_s L⁻³); X _b is the concentration of suspended biomass in the bulk liquid (M_x L⁻³); X _b0 is the initial suspended biomass in the reactor (M_x L⁻³); Q is the flow rate of the feed (L³ T⁻¹); V is the effective reactor volume (L³); A is the total surface area of media (L²); and ε is the porosity of the reactor (dimensionless).

Model solution

Two second-order partial differential equations with three ordinary differential equations can be simplified and converted to dimensionless forms by defining the dimensionless variables. Since the 2-CP concentration profile is symmetric with the center of activated carbon, the Legendre polynomials (an even function) in spherical coordinate are used to approximate the exact 2-CP concentration profile. Shifted Legendre polynomials in planar geometry are used to approximate the 2-CP concentration profile in biofilm. Two partial differential equations in dimensionless form can be converted to ordinary differential equations by orthogonal collocation method (OCM). The entire model system including 15 ordinary differential equations was solved by using Gear’s method to determine the 2-CP concentration profiles in activated carbon and biofilm, the growth of biofilm, the effluent concentrations of 2-CP, and suspended biomass in bulk liquid.

Model validation

The reduced root-mean-square (RMS) value provides a quantitative comparison of the agreement between the model prediction and experimental data. The lower RMS value represents the higher agreement between predicted and experimental data. The RMS deviation is given by (Kim and Kim 2004)

$${\text{RMS}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\frac{{\left( {C_{\text{exp,i}} - C_{\text{pred,i}} } \right)^{2} }}{{C_{\text{exp,i}}^{ 2} }}} } ,$$

(15)

where C _exp,i and C _pred,i are 2-CP concentrations of experiment and model prediction, respectively, and N is the number of data points.

Materials and methods

Preparation of a 2-CP-degrading seed inoculum

The seed sludge was taken from an anaerobic digester of the municipal sewage treatment plant, Taichung, Taiwan. It was incubated at 37°C with approximately 10 mg L⁻¹ of 2-CP and its biodegradation was monitored. Upon complete removal after about 4 weeks, this sludge was spiked again twice with 2-CP to enrich 2-CP degrading bacteria. Then the sludge or the turbid supernatant containing the bacteria was used for further experiments.

Supporting media

The specifications of G-340 were described as follows: particle size: 8 × 30 mesh; mean particle diameter: 0.9–1.1 mm; hardness: >93%; bulk density: 0.46–0.50 g cm⁻³; total surface area: >950 m² g⁻¹. Therefore, the total surface area was approximately 8.675 × 10⁴ cm².

Reactor design

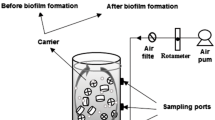
A continuous biological activated carbon was started by introducing the supernatant of the previously 2-CP-acclimated sludge after gravity sedimentation of the solids for 2 h as a seed inoculum. The BAC reactor (Fig. 2) consisted of a glass cylinder which was 70% packed with activated carbon as a supporting medium for biofilm attachment. The reactor porosity was 45.6%. One plastic sieve was provided at the top of packing activated carbon to fix the activated carbon in place and to avoid initial floating. The effective working volume of BAC reactor was 1.6 L, which yielded a hydraulic retention time (HRT) of 5 days. The reactor was maintained at 37 ± 0.2 °C through a water jacket using a circulating water bath (Yih Der Inc., Taipei, Taiwan). The influent was provided at the bottom using a peristaltic pump (Model HT100IJ, Longer Pump, China). The recirculation loop was equipped with a trigeminal tube to connect silicone tubing. The recycle pump was a peristaltic pump (Model 7554-80, Masterflex L/S, Cole Parmer Instrument Company, Chicago, IL, USA), but had higher capacity than the feed pump. The recycle ratio (Q _r/Q) was set at 25 to reach a nearly completely mixed condition in the column reactor. The influent feed was a synthetic wastewater (SWW) consisting of 2-CP as a main carbon substrate. The SWW was deoxygenated by purging nitrogen for 5 min and then initial 2-CP concentration of 190.5 mg L⁻¹ was added (Chang et al. 2003). The SWW was prepared in a phosphate buffer (NaH₂PO₄ of 6 g L⁻¹ and Na₂HPO₄ of 7.1 g L⁻¹) of pH 7.03 that contains the following nutrients or salts: peptone, 0.12 g; yeast extract, 0.12 g; NaCl, 0.007 g; MgSO₄·7H₂O, 0.002 g; CaCl₂·2H₂O, 0.004 g, and 200 µL of a trace metal solution per liter of distilled/deionized water (Bajaj et al. 2008). Trace metal solution consisted of FeSO₄·7H₂O, 1.36 g; Na₂MoO₄·2H₂O, 0.24 g; CuSO₄·5H₂O, 0.25 g; ZnSO₄·7H₂O, 0.58 g; NiSO₄·6H₂O, 0.11 g; MnSO₄·H₂O, 1.01 g; and H₂SO₄ 1 ml per liter of distilled/deionized water (Sarfaraz et al. 2004). Samples for analysis were periodically taken from the feed and effluent.

Fig. 2

A laboratory-scale biological activated carbon system

Adsorption experiments

Adsorption isotherm studies were conducted for 2-CP to evaluate the GAC adsorption capacities These experiments were performed in 250 mL serum bottles shaken at 120 rpm at 37°C. For determination of the adsorption isotherm, different masses of activated carbon of 1–20 g were conducted with 200 mL of 50 mg L⁻¹ initial 2-CP concentration and the mixture was agitated until reaching equilibrium. The time required for reaching an equilibrium of 2-CP concentration is the equilibrium time for adsorption. Equilibrium time was described as the time when 2-CP concentration reached a constant value. Initial and final equilibrium concentrations in the adsorption serum bottles were measured and used for the construction of adsorption isotherm. The Freundlich capacity constant, K _p, and the Freundlich intensity, 1/n, were determined by regression analysis of the isotherm data.

Batch biokinetic tests

The ability of anaerobic granules to degrade 2-CP was evaluated in 250 mL serum bottles which contained the nutrient medium mentioned above. Batch tests were carried out to determine specific growth rate of 2-CP degrading bacteria at an initial concentration of 2-CP ranging from 50 to 500 mg L⁻¹ by using BAC-reactor effluent as an inoculum. To accumulate more biomass, the treated wastewater was collected over days 119–146 of reactor operation and stored at 37 °C. Before using biomass for batch tests, it was allowed to sediment and the turbid lower layer was utilized as an inoculum. For each batch, 25 mL of anaerobic granules was added into the bottle. Serum bottles were then shaken at 37 °C at 120 rpm for 72 h and assayed. All experiments were performed in triplicate.

The initial 2-CP concentration of 200 mg L⁻¹ and mineral salt medium with biomass concentration of 8.4 mg VSS L⁻¹ in the batch reactor were used to evaluate 2-CP biodegradation. The reactor with an effective working volume of 5 L was maintained at a temperature of 37 ± 0.2 °C by a water jacket and a mixing speed of 200 rpm using a rotated shaft. Pure nitrogen at a rate of 1.2 L min⁻¹ was used to purge dissolved oxygen from reactor for maintaining anaerobic conditions. Liquid sample volume of 2 µL was taken out with a 10 µL syringe, previously flushed with nitrogen gas to analyze 2-CP as described below.

Analytical methods

The concentration of 2-CP and phenol were determined by HPLC–UV using a Alliance 2695 liquid chromatograph (Waters, Milford, MA, USA). The HPLC apparatus consisted of a Waters 2707 autosampler and a Waters 2487 UV/vis detector and was equipped with a Supelcosil LC-8 (Supelco, Bellefonte, USA). The column size is 4.6 mm in diameter with a height of 15 cm. The samples were eluted at 1.0 ml min⁻¹ with a mobile phase composed of methanol/water/acetic acid (60/39/1, v/v) for 20 min at a temperature of 30°C. The UV/vis spectrophotometric detector was set at 280 nm. The retention time for phenol and 2-CP was about 3.8 and 4.7 min, respectively. The 2-CP concentration adhered to the following regression equation: 2-CP (mg L⁻¹) = −0.30882 + 1.2019 × 10⁻⁵ (area), r ² = 0.9992. The phenol concentration was characterized by the following regression equation: phenol (mg L⁻¹) = 0.068217 + 1.435×10⁻⁵ (area), r ² = 0.9978. Measurement of volatile suspended solids (VSS) and chloride were conducted in accordance with the Standard Methods (APHA 2005). Samples of seed and acclimated sludge were lyophilized for 48 h using 2.5 L benchtop freeze dry system (Labconco Corporation, MO, USA). Morphology and surface structure of anaerobic sludge were then observed qualitatively with scanning electron microscope (SEM) (Hitachi model S-3000N, Japan).

Biokinetic parameters determination

The specific growth rate of biomass in a batch system, μ (d⁻¹), is defined as (Pollard and Greenfield 1997):

$$\mu = \frac{1}{X}\frac{{{\text{d}}X}}{{{\text{d}}t}} = \frac{{{\text{d}}\ln X}}{{{\text{d}}t}},$$

(16)

where X is the biomass concentration in mg L⁻¹. The value of μ is determined at the exponential phase of the growth curve.

Expression of μ in Eq. (16) represents the specific growth rate of biomass on single substrate, which is a function of the substrate concentration (Juang and Tsai 2006). The Haldane model was tried here due to its wide applicability for representing the growth kinetics of inhibitory substrates (Wang and Loh 1999):

$$\mu = \frac{{\mu_{\text{m}} S}}{{K_{\text{s}} + S + \left( {{{S^{2} } \mathord{\left/ {\vphantom {{S^{2} } {K_{\text{i}} }}} \right. \kern-0pt} {K_{\text{i}} }}} \right)}},$$

(17)

where μ is the specific growth rate (T⁻¹); S is the 2-CP concentration (M_s L⁻³), and μ _m is the maximum growth rate (T⁻¹). A larger K _i value indicates that the microorganisms are less sensitive to substrate inhibition (Onysko et al. 2000).

The Haldane kinetics for 2-CP utilization in the batch reactor can be described as (Pirbazari et al. 1996)

$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \frac{\mu X}{Y},$$

(18)

where X is the biomass concentration (M_s L⁻³). The relation between the growth rate of biomass and utilization rate of 2-CP can be represented by

$$\frac{{{\text{d}}X}}{{{\text{d}}t}} = - Y\left( {\frac{{{\text{d}}S}}{{{\text{d}}t}}} \right)$$

(19)

For small changes in the 2-CP degrading bacteria and concentration of 2-CP in the growth phase, Eq. (19) can be integrated to yield the following relation:

$$X = X_{0} + Y\left( {S_{0} - S} \right),$$

(20)

where X ₀ and X are initial biomass concentration (M_x L⁻³) and biomass concentration (M_x L⁻³) in the batch system, respectively, and S ₀ and S are initial 2-CP concentration (M_s L⁻³) and 2-CP concentration (M_s L⁻³) in the batch system, respectively. The slope of a linearized plot of (X − X ₀) versus (S ₀− S) is the growth yield (Y).

The experimental data in the endogenous phase can be used for estimating the microbial decay rate. The biomass decay rate can be expressed by

$$r_{\text{x}} = \frac{{{\text{d}}X}}{{{\text{d}}t}} = - bX$$

(21)

The equation can be integrated to yield the relation

$$b = - \frac{{\ln \left( {{{X_{1} } \mathord{\left/ {\vphantom {{X_{1} } {X_{0} }}} \right. \kern-0pt} {X_{0} }}} \right)}}{{t_{1} - t_{0} }},$$

(22)

where X ₁ and X ₂ are biomass concentration at t ₁ and t ₂ in the batch system. The decay rate of biomass, b, can thus be determined from the slope of a linearized plot of lnX versus time in the endogenous phase (Pirbazari et al. 1996).

Determination of mass transfer coefficients

The diffusion coefficient of 2-CP in bulk liquid (D _w) was determined from the empirical formula (Wilke and Chang 1955). The formula can be expressed by the following equation:

$$D_{\text{w}} = 7.4 \times 10^{ - 8} \frac{{\left( {\phi_{\text{b}} M_{\text{b}} } \right)^{0.5} T}}{{\mu_{\text{b}} V_{\text{a}}^{0.6} }},$$

(23)

where ϕ _b is association parameter; M _b is molecular weight of water; T is absolute temperature in K; μ _b is absolute viscosity of the solution in centipoises for water; and V _a is molar volume of the solute as liquid at its normal boiling point. Molar volumes of solutes can be estimated from the atomic volume of their atoms (Perry and Chilton 1973). The computed value of D _w is equal to 1.021 cm² d⁻¹. The diffusion coefficient in the biofilm is obtained by multiplying the diffusion coefficient in the bulk liquid phase by a factor of 0.8 to correct the additional diffusional resistance in the biofilm (Williamson and McCarty 1976). Thus, the diffusion coefficient of 2-CP in biofilm (D_f) was equal to 0.817 cm² d⁻¹.

The liquid–film transfer coefficient (k _f) computed from the empirical formula for the packed-bed adsorber was described in the following equation (Williamson et al. 1963):

$$k_{\text{f}} = 2.4v_{\text{s}} \left( {\frac{{R_{e} }}{\varepsilon }} \right)^{ - 0.66} \left( {S_{c} } \right)^{ - 0.58} ,$$

(24)

where $v_{\text{s}}$ is the superficial flow velocity through column (LT⁻¹); $R_{e}$ is Reynolds number = $\frac{{d_{\text{p}} v_{\text{s}} }}{v}$; $S_{c}$ is Schmidt number = $\frac{\upsilon }{{D_{\text{w}} }}$; d _p is the diameter of the ceramic particle (L); and $\upsilon$ is the kinematic viscosity (L² T⁻¹). The value of k _f computed by Eq. (24) was equal to 117.9 cm d⁻¹.

An empirical formula suitable for spherical particle was used to evaluate specific shear-loss coefficient (b _s) of the biofilm on activated carbon (Speitel and DiGiano 1987):

$$b_{\text{s}} = 2.29 \times 10^{ - 6} \left[ {\frac{{V_{\text{w}} v_{\text{s}} \left( {1 - \varepsilon } \right)^{3} }}{{d_{\text{p}}^{2} \varepsilon^{3} a}}} \right]^{0.58} ,$$

(25)

where V _w is water viscosity (M_s L⁻¹ T⁻¹); v _s the superficial fluid velocity (L T⁻¹); ε the bed porosity; d _p the diameter of medium (L); and a the specific surface area of the bed (L⁻¹). The computed value of b _s was equal to 9.53×10⁻³ d⁻¹.

Results and discussion

Adsorption kinetics in batch tests

Figure 3 shows the experimental time course plot of residual 2-CP concentration at different GAC dosages. The amount of adsorbed 2-CP depended on the dosages of activated carbon. It is observed that the amount of 2-CP adsorbed increased as the GAC dosages increased. The adsorbed rate of 2-CP contents was steeper with high GAC dosage of 20 g than low GAC dosage of 1 g before reaction time of 2 h. However, the adsorbed rate of 2-CP contents increased as the GAC dosages decreased after reaction time of 2 h. The time required for complete removal of 2-CP with an initial concentration of 50 mg L⁻¹ was 10 h.

Fig. 3

Variation of residual concentration of 2-CP with time at different GAC dosages

Adsorption isotherm parameters

Empirical Freundlich equation based on sorption on a heterogeneous surface was used for approximation of obtained results (Sirotkin et al. 2001). The logarithmic form of the Freundlich isotherm was employed to compute the parameters by linear regression:

$$\log q_{\text{p}} = \log K_{\text{p}} + \frac{1}{n}\log S_{\text{p}}$$

(26)

A plot of log q _p versus log S _p should yield a straight line. K _p was computed from the y-interception and n was computed from the slope of regression. The values of K _p and n obtained from Fig. 4 were equal to 0.57 (mg g⁻¹)(L mg^−1)0.85 and 1.17, respectively.

Fig. 4

Freundlich adsorption isotherm to determine Freundlich isotherm constant (K _p, n)

Effective diffusivity

The intraparticle diffusion model (Eq. 1) and 2-CP adsorption kinetic model in bulk liquid were integrated to simulate adsorption kinetic test to evaluate effective diffusivity (D _ef) of 2-CP. The 2-CP adsorption model in bulk liquid can be expressed by (Chang et al. 2000)

$$\frac{{{\text{d}}S_{\text{b}} }}{{{\text{d}}t}} = - \frac{{3X_{\text{w}} k_{\text{f}} }}{{V\varepsilon \rho_{\text{a}} R_{\text{a}} }}\left( {S_{\text{b}} - S_{\text{w}} } \right),$$

(27)

where S _w is the 2-CP concentration at liquid–carbon interface (mg L⁻¹). The comparison of experimental data and model prediction for 2-CP adsorption in batch test was plotted in Fig. 5. The best-fit D _ef value was obtained with regression analysis, which was equal to 6×10⁻⁴ cm² d⁻¹.

Fig. 5

Batch kinetic test for 2-CP adsorption, effective working volume = 200 mL, activated carbon = 5 g, and initial 2-CP concentration = 50 mg L⁻¹

Acclimation of sludge to 2-CP in a batch reactor

Anaerobic sludge was supplemented with 2-CP and nutrient media in a batch reactor to obtain a 2-CP acclimated culture. Figure 6 presents the concentrations of 2-CP and phenol varied over time during acclimation. The time required for complete degradation of 10 mg L⁻¹ by anaerobic sludge was 28 days. The degradation time was improved by 15 days upon the second addition of the same amount of 2-CP. When the sludge was spiked a third time with 2-CP, complete removal of 10 mg L⁻¹ took only 9 days. Quick successive feeding of 2-CP upon complete depletion reduced the time required for complete degradation.

Fig. 6

Acclimation of anaerobic sewage sludge to 2-chlorophenol

The intermediate product of 2-CP dechlorination, phenol, was detected during the acclimation phase. The phenol was considered to be rapidly produced as soon as it was derived from the 2-CP dechlorination. Up to 1.2 mg phenol L⁻¹ accumulated when the 2-CP concentration decreased to about 9 mg L⁻¹ at the start phase of acclimation; then the phenol concentration started to decline up to complete degradation (Fig. 6). No lag phase was observed for phenol accumulation during the period of acclimation. During batch acclimation of anaerobic sludge to 2-CP, phenol accumulation for a short time was observed. This may be due to a higher rate of dechlorination of 2-CP compared to the rate of phenol degradation at surplus substrate availability during the acclimation phase (Bajaj et al. 2008). Wang et al. (1998) reported that the time required for the complete transformation of 10 mg L⁻¹ of 2-CP was 35 days in a methanogenic enrichment culture of a wastewater treatment plant. Ye and Shen (2004) conducted chlorophenol acclimation studies on two types of sludge under batch mode. They also had found a relatively rapid degradation rate of 2-CP with municipal wastewater sludge after 2 months of incubation with successive feedings.

Prior to acclimation, the seed sludge was found to be darkish black and its structure was fluffy, irregular, and loose (Fig. 7a). The acclimated sludge was observed after the acclimation period of 52 days and its structure was dispersed with the amorphous sludge flocs (Fig. 7b). The SEM results were similar to those observed by Ning et al. (1997) and Wang et al. (2007). Their studies found that the structure of acclimated sludge was granular flocs.

Fig. 7

Anaerobic sludge morphology a seed sludge and b acclimated sludge

Biokinetic parameters

Figure 8 illustrates the variation of specific growth rate (μ) with initial concentration of 2-CP. The specific growth rate increased with the increasing initial 2-CP content up to 250 mg L⁻¹, peaked at 0.14 d⁻¹, but then decreased for the initial contents between 250 and 500 mg L⁻¹, indicating the inhibitory effect of 2-CP at a concentration exceeding 250 mg L⁻¹. Therefore, the Haldane equation was used to model the specific growth rate of anaerobic mixed culture (Juang and Tsai 2006). The Haldane equation for substrate-inhibited growth was fitted to the data of specific growth rate (μ) as a function of 2-CP concentration (S) using a non-linear least-square error technique (Kumar et al. 2000). The biokinetic parameters estimated with the non-linear least-square regression method were μ _m = 0.375 d⁻¹; K _s = 127 mg L⁻¹, and K _i = 105.3 mg L⁻¹, with a correlation coefficient (r ²) of 0.994. Therefore, the resulting kinetic equation is as below:

Fig. 8

Specific growth rate of anaerobic sludge at different initial 2-CP concentration

$$\mu = \frac{0.375S}{{127 + S + \frac{{S^{2} }}{105.3}}}$$

(28)

These values agreed reasonably well with the values obtained by Sivawan (1997) (K _s = 152 mg L⁻¹, K _i = 116.27 mg L⁻¹) for 2-CP biodegradation by anaerobic sludge in an upflow anaerobic sludge blanket (UASB) reactor.

The kinetic batch experiments were conducted to determine the growth yield (Y), maximum specific utilization rate (k), and the decay rate (b). The variation of 2-CP and biomass concentration versus time is depicted in Fig. 9. It can be observed that the data of biomass concentration represent a typical growth and decay curve with a well-defined growth phase and the endogenous phase (Pirbazari et al. 1996). The concentration data of 2-CP and biomass facilitate a priori estimation of biokinetic parameters for evaluating the utilization rate of 2-CP and growth rate of biomass. The relevant techniques employed for the evaluation of biokinetic parameters (Y, k and b) from the data of batch experiments are discussed below.

Fig. 9

Batch kinetic data on the variation of 2-CP and suspended biomass

The growth yield (Y) for biomass is assumed approximately constant over the range of 2-CP concentration encountered in the growth phase. The growth for biomass determined from the slope of linearized plot of (X − X₀) versus (S ₀ − S) is shown in Fig. 10a. The growth yield for biomass was 0.044 mg VSS mg⁻¹ 2-CP with a correlation coefficient (r ²) of 0.996. The maximum specific utilization rate (k) of 2-CP can be computed by µ _m/Y. The k value for biomass was 8.52 mg 2-CP mg⁻¹ VSS d⁻¹. The decay coefficient of biomass can be determined from the slope of linearized plot of lnX versus time presented in Fig. 10b. The value of decay coefficient for biomass was 0.0126 d⁻¹ with a correlation coefficient (r ²) of 0.999.

Fig. 10

Batch kinetic test to determine a growth yield of biomass (Y) and b decay rate of biomass (b)

2-CP adsorption and biodegradation

Table 1 presents the biokinetic and reactor parameters as well as mass transfer coefficients obtained from batch kinetic tests, which were used for the kinetic model prediction. The column test using activated carbon as the supporting medium was conducted to investigate the kinetics of 2-CP in an anaerobic BAC process. The model-generated and experimental results of 2-CP adsorption and biodegradation by attached and suspended biomass for column test are shown in Fig. 11a. The model simulated the experimental results well throughout the entire courses of the test. The performance of the BAC process can be described by four parts. First, the 2-CP concentration increased steadily up to about 25.5 mg L⁻¹ (0.134 S _b0) at 10 days. During this period, the growth of 2-CP degrading bacteria inside the reactor for 2-CP degradation was not significant. The reactor was behaving similar to an activated carbon adsorber. At this stage, activated carbon was adsorbing 2-CP without significant resistance to the diffusion of the 2-CP posed by the attached biomass.

Table 1 Operation conditions and biokinetic parameters used for model prediction

Fig. 11

Model prediction and experimental data a 2-CP effluent concentration b biofilm growth c suspended biomass concentration in effluent d fluxes into biofilm and activated carbon e chloride production and f amount of 2-CP removal

The second part of 2-CP curve ran from 10 to 38 days, when the 2-CP curve started to deviate from the breakthrough curve of activated carbon adsorber. The 2-CP effluent concentration leveled off and then began to decrease during this period of time. Both phenomena confirm the active degradation of 2-CP by attached biomass and that biofilm was growing significantly during the second period. The third part of the 2-CP curve ran from 38 to 146 days. The 2-CP concentration maintained a constant level which represented the steady-state condition. The 2-CP concentration was approximately 2.9 mg L⁻¹ (0.0152 S _b0) during this period. The 2-CP concentration reached a steady-state level, which was equivalent to about 98.5% removal efficiency for 2-CP. The model prediction is in good agreement with the experimental result with a reduced root-mean-square (RMS) deviation of 0.139.

Growth of biofilm

Figure 11b presents the growth curve of biofilm that varied with time by model prediction for biofilm on activated carbon from non-steady-state to steady-state condition. The growth curve of biofilm shows a similar pattern to suspended biomass (Fig. 11c). The elapsed time required for biofilm to start to grow is approximately 5 days. The biofilm vigorously grew to degraded 2-CP from 5 to 21 days. At a steady-state condition, the maximum growth thickness of biofilm reached up to 636 μm by BAC model prediction.

Growth of suspended biomass

Figure 11c shows that the growth curves of suspended biomass varied with time. One indicator of the increased biomass growth was the concentration of suspended biomass in the effluent. The concentration of initial suspended biomass was set at 4.8 mg VSS L⁻¹ that was experimentally determined at the start of continuous-flow column test. In the beginning of the column test, the concentration of suspended biomass dropped abruptly and then started to increase with time due to the dilute-in characteristics (Gaudy and Gaudy 1980). The general trend of the effluent for suspended biomass concentration in model prediction was similar to the experimental results obtained from the column test. The model-predicted and experimental results show that there was no significant degradation of 2-CP by suspended biomass for the first 5 days. The growth rate of suspended biomass rapidly increased at a transient-state condition from 5 to 27 days. At this period, the suspended biomass vigorously degraded 2-CP. Since the amount of 2-CP available during bioregeneration was higher than after bioregeneration of activated carbon, the growth rate of suspended biomass during this period should have been higher than that at the steady-state level. The growth curve of suspended biomass showed a peak at 27 days during bioregeneration. The concentration of suspended biomass in effluent was approximately 25.3 mg VSS L⁻¹ at the steady state. The model predicted the experimental result well with a reduced root-mean-square (RMS) deviation of 0.239.

Fluxes into biofilm and activated carbon

The 2-CP flux into biofilm increased with the growth of biofilm during the transient period when the mechanisms of diffusion and biodegradation are considered in the biofilm model. However, the mechanisms considered in BAC model include adsorption, diffusion, and biodegradation in this study. Figure 11d presents the flux of 2-CP into biofilm (J _f) along with the flux of 2-CP into activated carbon (J _q). The figure shows that the values of J _f and J _q were equal and started out a larger value that was controlled totally by adsorption at the beginning of the test because 2-CP degradation by biofilm was negligible at this time. Most of 2-CP was removed by adsorption of activated carbon at the start of column test.

The curves of J _f and J _q started to deviate with each other around 5 days, when the biofilm started to grow actively. The J _f decreased rapidly as the biofilm start to grow from 0 to 19 days because adsorption slowed the development of a biofilm by decreasing the 2-CP concentration “seen” by the biofilm during this period of time. Then, the J _f began to increase reversely after bioregeneration of activated carbon from 19 to 58 days because the flux was diffusing from activated carbon into biofilm, which represented the desorption of the 2-CP. In sequence, J _f reached a constant level at the steady-state condition after J _q approached zero and 2-CP removal was initially dominated by biofilm.

The curve of J _q shows a positive flux of the 2-CP into activated carbon from 0 to 11 days. The J _q showed a maximum value in the beginning of the test, because biofilm growth was negligible and the diffusion resistance was minimal. The J _q decreased as 2-CP started to accumulate inside the activated carbon, thus lowering the concentration gradient at the exterior surface of activated carbon. The most important point was that at 11 days, the flux changed from a positive value to a negative value. A positive J _q means 2-CP was diffusing from biofilm into activated carbon, while a negative J _q means 2-CP was diffusing from activated carbon into biofilm. This required a reversal of the concentration profile inside the activated carbon. The resulting negative concentration gradient caused the 2-CP to diffuse out of the activated carbon for a bioregeneration start. As the biofilm accumulated to grow thicker, the resistance to the diffusion of 2-CP became larger, and the biofilm degraded 2-CP to lower 2-CP concentration at biofilm-carbon interface. The 2-CP concentration continued to decrease to a level where the equivalent surface concentration in the activated carbon was lower than the equilibrium with previously adsorbed 2-CP. A reversal in the concentration profile was then established. At this point, 2-CP simply diffused out of the activated carbon and activated carbon was bioregeneratd by the biofilm.

As the steady-state approached, J _q went to zero asymptotically from a negative value, while J _f approached a constant value equal to 6.42 × 10⁻² mg cm⁻² d⁻¹. The curves shows that 2-CP biodegradation by biofilm became the dominant mechanism responsible for the steady-state removal of 2-CP in the BAC process.

Chloride release in the BAC process

The removal of 2-CP starts with dehalogenation of 2-CP, accompanied by the production of inorganic chloride ions. It can be deduced from the reaction stoichiometry that 0.28 g of inorganic chloride must be released during dechlorination of 1 g 2-CP. Figure 11e presents the observed and expected chloride ion production varied with time. In this study, the inoculum already contained chloride. Therefore, the concentration of chloride was higher than that expected from complete dechlorination after start-up. The concentration of chloride was diluted about 7 days to a concentration that could stem from 2-CP dechlorination at a HRT of 5 days (Bajaj et al. 2008). The ratio of chloride released per unit of 2-CP removed was then close to the theoretical value but still higher than that expected from complete dechlorination. The observed range from day 10 to day 146 of reactor operation was 0.282–0.315 with 0.295 as the average ratio and 0.294 as the median value, indicating very little fluctuation in dehalogenation of 2-CP during the study period.

2-CP removal by model prediction

The 2-CP removed by the entire system was the summation of the 2-CP removed by the biofilm and the adsorption by activated carbon. Figure 11f shows the amount of 2-CP removed by the entire system, activated carbon, and biofilm in a BAC process. Since 2-CP removed by adsorption does not change its chemical structure, the amount of 2-CP removed by the activated carbon also equals the amount of 2-CP that remains adsorbed in the activated carbon.

The amount of 2-CP removed by the entire system was equal to 2-CP adsorbed by activated carbon up to 10 days. Biofilm utilized almost no 2-CP, because the amount of the 2-CP degrading bacteria was not significant up to this time. As the biofilm started to grow actively after 10 days, 2-CP removed by biofilm increased and that adsorbed by the activated carbon leveled-off. The 2-CP removal was dominated by the adsorption of activated carbon prior to 11 days of the column test. The amount of 2-CP adsorbed by activated carbon decreased after 11 days due to bioregeneration. The adsorbed amount of the 2-CP was then decreasing slowly since 2-CP was beginning to diffuse out from the activated carbon after bioregeneration. During the period from 15 to 80 days, the 2-CP removal by adsorption was slightly decreasing because the J _q was beginning to increase from the lowest point of value. The 2-CP removal by adsorption was then reached a steady-state condition after 80 days since the value of J _q was maintained at around zero after day 80 until the termination of the column test. As a result, the activated carbon was only acting essentially as a supporting medium for biofilm growth at the steady state.

2-CP concentration profiles

The concentration profiles at 7.1, 29.2, 50, 70.8, and 137 days in the diffusion layer, biofilm, and activated carbon, computed by BAC model, are plotted in Fig. 12. At 7.1 days, biofilm was 47.3 μm thick, and 2-CP adsorption reached a high value. A positive flux ($J_{\text{q}}$) (Fig. 11d) was diffusing from biofilm into activated carbon to make a high concentration profile in the activated carbon. Activated carbon was adsorbing 2-CP significantly at this time. The biofilm at this stage could be called “fully penetrated” according to the definition of Rittmann and McCarty (1981). The concentration profile that occurred in activated carbon changed to a different pattern at 29.2 days. At this time, bioregeneration occurred and 2-CP diffused out of activated carbon then degraded by biofilm. The thickness of biofilm was 142 μm at this time. The concentration profile pattern at 50 days was similar to that at 29.2 days. At 50 days, the 2-CP concentration in activated carbon was lower than that at 29.2 days since more 2-CP diffused out of activated carbon for biodegradation by attached biomass due to bioregeneration. The BAC process had reached a steady state from 70.8 to 137 days. At this period, the concentration profiles presented a similar pattern of flat line in the activated carbon, biofilm, and diffusion layer. The biofilm had almost completely stopped bioregenerating activated carbon since the concentration profile of 2-CP was relatively flat in activated carbon at this period.

Fig. 12

Concentration profiles in diffusion layer, biofilm, and activated carbon at different times

Conclusions

As can be derived from this study, the acclimatization strategy seems to play an important role in successful treatment of toxic compounds such as 2-CP. Acclimation to the biodegradation of approximately 10 mg L⁻¹ of 2-CP was possible within less than 10 days. The removal efficiency increased considerably with successive feedings. The acclimated sludge could be used as an inoculum for an anaerobic BAC reactor to achieve high 2-CP removal efficiency under continuous-flow condition. The mathematical model system was derived to describe the adsorption and biodegradation of 2-CP by 2-CP degrading bacteria in BAC process. The completely mixed, packed-bed BAC process was conducted to validate the model. The experimental data and model simulation in effluent concentration of 2-CP agreed well with each other. The 2-CP flux across the biofilm–carbon interface quantitatively illustrated bioregeneration rate. Concentration profiles of 2-CP in the activated carbon showed a complete reversal as 2-CP was diffusing out of the activated carbon during the period of bioregeneration. Biofilm bioregenerated the activated carbon by lowering the 2-CP concentration at the biofilm-activated carbon interface as the biofilm grew thicker. The 2-CP previously adsorbed inside the activated carbon simply desorbed out of the activated carbon through a reversal of the concentration profile in the activated carbon. The experimental data and model simulation in effluent concentrations of 2-CP and suspended biomass agreed well with each other. The results of this study can be applied to aid the design and operation of the biological activated carbon process.

Appendix

2-CP utilization rate

The concepts and kinetic models for suspended-growth and attached-growth substrate utilization rate were developed and verified by many researchers (Williamson and McCarty 1976; Tchobanoglous 1991; Chang and Rittmann 1987a, b). For the suspended biomass, Haldane kinetic equation is commonly used to calculate the 2-CP utilization rate by suspended biomass (R _us) (Tchobanoglous 1991)

$$R_{\text{us}} = \frac{{kS_{\text{b}} }}{{K_{\text{s}} + S_{\text{b}} + \frac{{S_{\text{b}}^{ 2} }}{{K_{\text{i}} }}}}X_{\text{b}} V\varepsilon$$

For the attached biomass, a substrate concentration profile is established in the biofilm due to the diffusional resistance to the transport of the substrate. To calculate the 2-CP utilization rate (R _ua) by the biofilm, the utilization rate within a differential thickness (dz _f) must be integrated over the entire thickness of the biofilm (L _f).

$$R_{\text{ua}} = Va\int_{0}^{{L_{\text{f}} }} {\frac{{kS_{\text{f}} }}{{K_{\text{s}} + S_{\text{f}} + \frac{{S_{\text{f}}^{ 2} }}{{K_{\text{i}} }}}}} X_{\text{f}} {\text{d}}z_{\text{f}} = VaJ_{\text{f}}$$

Figure 13a presents the 2-CP utilization rate by suspended biomass (R _us) that varied with time. The R _us first increased steadily to about 2.1 mg d⁻¹ at 12.5 days due to the significant growth of suspended biomass. The second part of R _us curve ran from 12.5 to 37.5 days. The R _us decreased rapidly during this transient period of time. The third part of R _us curve ran from 37.5 to 146 days and reached a steady-state condition. At this period, the R _us reached a constant value of approximately 0.7 mg d⁻¹. The comparison of model prediction with experimental results for R _us is satisfactorily acceptable with a correlation coefficient (r ²) of 0.906. Figure 13b shows the 2-CP utilization rate by biofilm (R _ua) that varied with time. The trend of R _ua in Fig. 13b is very similar to the flux into biofilm in Fig. 11d. The R _ua decreased rapidly from 8399 to 4844 mg d⁻¹ as the biofilm started to grow from 0 to 19 days because adsorption slowed the development of a biofilm by decreasing the 2-CP concentration “seen” by the biofilm during this period of time. Then, the R _ua began to increase reversely after bioregeneration of activated carbon from 19 to 58 days because the flux was diffusing from activated carbon into biofilm. In sequence, R _ua reached a constant level at the steady-state condition from 58 to 146 days. Comparing the value of R _us with R _ua, the R _ua value is greatly higher than R _us value, which indicated that the amount of overall substrate utilization of 2-CP is almost achieved by biofilm. However, suspended biomass only contributed to a small amount of overall substrate utilization in BAC reactor. The biofilm which degrades substrate at a much higher rate is the dominant form of the biomass in the BAC reactor.

Fig. 13

2-CP utilization rate by a suspended biomass b biofilm