Water quality modeling for urban reach of Yamuna river, India (1999–2009), using QUAL2Kw

Abstract

The study was to characterize and understand the water quality of the river Yamuna in Delhi (India) prior to an efficient restoration plan. A combination of collection of monitored data, mathematical modeling, sensitivity, and uncertainty analysis has been done using the QUAL2Kw, a river quality model. The model was applied to simulate DO, BOD, total coliform, and total nitrogen at four monitoring stations, namely Palla, Old Delhi Railway Bridge, Nizamuddin, and Okhla for 10 years (October 1999–June 2009) excluding the monsoon seasons (July–September). The study period was divided into two parts: monthly average data from October 1999–June 2004 (45 months) were used to calibrate the model and monthly average data from October 2005–June 2009 (45 months) were used to validate the model. The R² for CBODf and TN lies within the range of 0.53–0.75 and 0.68–0.83, respectively. This shows that the model has given satisfactory results in terms of R² for CBODf, TN, and TC. Sensitivity analysis showed that DO, CBODf, TN, and TC predictions are highly sensitive toward headwater flow and point source flow and quality. Uncertainty analysis using Monte Carlo showed that the input data have been simulated in accordance with the prevalent river conditions.

Introduction

The water management strategies transform with changing pattern of a metropolis that alters the urban reach of a river basin. The urban reach of any river system is one of the most exploited environmental resources as it is subjected to discharge from treated and untreated wastewater, storm water, and combined sewage. It is also negatively impacted by shoreline encroachment, flood control channelization, erosion, sedimentation, etc. (Walsh et al. 2005; Paul and Meyer 2001; Mathew et al. 2011). Pollutants, when discharged into a river system, change their physical, chemical, and biological characteristics—depleting the dissolved oxygen (DO) and augmenting the organics like carbon, nitrogen, etc. This speeds up the eutrophication process in the river (Cox 2003; Van der Velde et al. 2006; Kannel et al. 2010; Rusjan et al. 2008). In view of this, the Government of India (GoI) launched various river action plans to combat the river pollution for river Ganga, river Yamuna, etc. In order to maintain the water quality, it is important to know the levels and characteristics of the pollutant a river can assimilate without impacting its self-purification capacity (Glavan and Pintar 2010). The effective and efficient management of a river system along with the design and optimization of discharge regimes can be achieved by applying water quality models (WQMs) (Lopes et al. 2008; Glavan et al. 2011). They are useful to validate the pollutant load estimates to establish cause–effect relations between diverse sources of pollution and water quality and also to assess the response of the river system to different management scenarios.

The present study intends to evaluate the impacts of wastewater loadings on the water quality of the river Yamuna using QUAL2Kw which can be applied to small river basin. QUAL2Kw model and its earlier versions like QUAL2e, QUAL2e-UNCAS, and QUAL2K have been applied to various watershed for simulating different parameters and generating various management scenarios (Oliveira et al. 2011; Grabiç et al. 2011; Lin et al. 2010; Xiaobo et al. 2008; Fan et al. 2009; Kannel et al. 2007; Gardner et al. 2007; Azzellino et al. 2006). The successful applications of QUAL series model on the same study area (Paliwal et al. 2007; Parmar and Keshari 2011) implies that the model can be applied worldwide and can also provide basic knowledge for water quality assessment even with limited dataset. The Yamuna river in Delhi has high levels of pollution caused by the discharge of untreated or partially treated wastewater entering the river system directly or indirectly via wastewater drains. In order to restore the river quality to the designated class ‘C’ assigned by Central Pollution Control Borad (CPCB), the GoI initiated the Yamuna Action Plan (YAP) phase I in 1993 and later extended it to phase II in 2004. It was observed that even after the application of both phase I and phase II, desired class of the river stretch was not met due to high pollution load resulting from population escalation and limitation in treatment facilities (CPCB 2007; Sharma and Kansal 2011). In past, various pollution assessment studies have been done to simulate the DO–BOD water quality of the river Yamuna (Delhi stretch) (Bhargava 1983, 1986; Kazmi and Hansen 1997; Kazmi 2000; Kazmi and Agrawal 2005; Paliwal et al. 2007; Sharma and Singh 2009; Parmar and Keshari 2011), but no modeling has been done to assess the impact of other critical parameters like pathogens or nitrogenous compounds on the river quality. The present study was undertaken to address this limitation.

In the present study, the modeling was done for a period of 10 years (October 1999–June 2009), wherein QUAL2Kw model was calibrated and validated for DO, BOD, nitrogen, and total coliforms. The study excludes monsoon period (July–September) due to the fact that the water was observed to be of good quality as compared to the rest of the period due to high dilution capacity and reaeration properties (CPCB 2007; Sharma and Kansal 2011; Paliwal et al. 2007). A sensitivity analysis was done to quantify the error associated with the significant parameters. Finally, Monte Carlo Simulation (MCS) was done for uncertainty analysis using YASAIw (A Monte Carlo simulation add-in for Microsoft Excel) (Pelletier 2009) to compute the uncertainties associated with the water quality parameters and associated coefficients.

Description of study area

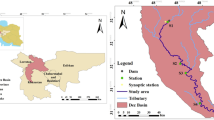
The present study has been done for the Delhi stretch of the river Yamuna. Delhi is a mega metropolis situated on the banks of the river Yamuna with an area of 1483 km² (0.4 % of total catchment). The population of the capital has increased from 13.8 million in 2001 to 16.7 million in 2011 (Indiastat.com 2012). According to a Memorandum of Understanding (MOU) signed in 1994, the river Yamuna would provide annual allocation of 724 MCM of water to Delhi (Jain 2009), approximately 70 % of Delhi’s water requirements (CPCB 2007). It enters from Palla traverses approximately 15 km and reaches Waziarabd barrage where most of the river water is abstracted for the water supply to the capital. Thereafter, very little freshwater flow is observed especially during summer. The river leaves the city at Jaitpur near Okhla Barrage (Fig. 1), which is approximately 39.4 km downstream (d/s) Palla (CPCB 2007). The total area of river zone is about 9700 Ha, out of which approximately 1600 Ha of land is under water and 8100 Ha is dry land which also causes direct runoff pollution into the river (Delhi master Plan 2021; Sharma et al. 2011).

Fig. 1

Schematic diagram of river Yamuna along with monitoring stations, tributary, abstractions, and drains in Delhi

The study was done for a period of 90 months and the model was calibrated for 4 monitoring stations, namely Palla (M1), Old Delhi Railway bridge (ODRB, M2), Nizamuddin (M3), and Okhla (M4). M1 is 15 km upstream (u/s) Wazirabad barrage near the flood control office. Thereafter, three other locations were chosen, namely M2 (approximately 20 km d/s Palla), M3 (approximately 28.28 km d/s Palla), and M4 (near Agra Canal; approximately 39.4 km d/s Palla), to assess the spatial and temporal distribution of water quality.

Methodology

Description of QUAL2Kw

It is a 1D model and can be applied to a river with approximately constant flow and the pollution load. It can simulate water quality constituents like temperature, electrical conductivity (EC), pH, Carbonaceous Biochemical Oxygen Demand (CBOD), Sediment Oxygen Demand (SOD), DO, Organic Nitrogen (ON), ${\text{NH}}_{4}^{ + }$, NO³⁻, NO²⁻, Inorganic Suspended Solids (ISS), Organic Phosphorus (OP), Inorganic Phosphorus (IP), phytoplankton, and bottom algae. It can also calculate Total Nitrogen (TN) and Total Phosphorous (TP). It can simulate reaeration, algal respiration and growth, organic matter degradation, mineralization, nitrification, denitrification, sedimentation, and benthic activity. The main input data include geometric properties of the river (including channel slope, channel width, side slope, and manning roughness coefficient), flow rate, pollutant loads, and meteorological parameters. In addition, it has genetic algorithms (GA) for automatic calibration, hyporheic metabolism, and simulation of the metabolism of heterotrophic bacteria in the hyporheic zone. It is programed in Visual Basic for Applications (VBA). Excel is used as the graphical user interface for input, running the model, and viewing the output. The numerical integration is performed by a compiled Fortran 95 program that is run by the Excel VBA program. The model framework and documentation are available for download from the Washington State Department of Ecology at (QUAL2Kw 2010; Pelletier et al. 2006; Chapra and Pelletier 2006; Pelletier and Chapra 2008). The QUAL2Kw model may represent a good framework for modeling the water quality of the river Yamuna.

Governing equations

Basic equation

$$\begin{aligned} \frac{{{\text{d}}c_{i} }}{{{\text{d}}x}} = \frac{{Q_{i - 1} }}{{V_{i} }}c_{i - 1} - \frac{{Q_{i} }}{{V_{i} }}c_{i} - \frac{{Q_{{{\text{ab}},i}} }}{{V_{i} }}c_{i} + \frac{{E'_{i - 1} }}{{V_{i} }}(c_{i = 1} - c_{i} ) \hfill \\ + \frac{{E'_{i} }}{{V_{i} }}(c_{i + 1} - c_{i} ) + \frac{{W_{i} }}{{V_{i} }} + S + \frac{{E'_{{{\text{hyp}},i}} }}{{V_{i} }}(c_{2,i} - c_{i} )_{i} \hfill \\ \end{aligned}$$

(1)

$$\frac{{{\text{d}}c_{2,i} }}{{{\text{d}}x}} = S_{2,i} + \frac{{E'_{{{\text{hyp}},i}} }}{{V_{2,i} }}\left( {c_{i} - c_{2,i} } \right);\frac{{{\text{d}}_{{{\text{ab}},i}} }}{{{\text{d}}x}} = S_{{{\text{b}},i}} ;\frac{{{\text{d}}IN_{\text{b}} }}{{{\text{d}}t}} = S_{{{\text{bN}},i}} ;\frac{{{\text{d}}IP_{\text{b}} }}{{{\text{d}}t}} = S_{{{\text{bp}},i}} ;\frac{{{\text{d}}a_{{{\text{h}},i}} }}{{{\text{d}}t}} = S_{{{\text{ah}},i}}$$

(2)

DO

$$\begin{aligned} S_{o} = r_{\text{oa}} \left( {{\text{PhytoPhoto}} - {\text{PhytoResp}}} \right) + r_{\text{od}} \left( {{\text{BotAlgPhoto}} - {\text{BotAlgResp}}} \right)\frac{{A_{{{\text{st}},i}} }}{{V_{i} }} \hfill \\ - r_{\text{oc}} {\text{FASTCOxid}} - r_{\text{oc}} {\text{SlowCOxid}} - r_{\text{on}} {\text{NH}}_{4} {\text{Nitr}} + {\text{Reaeration}} - {\text{COD}}_{\text{oxid}} - {\text{SOD}}\frac{{A_{{{\text{st}},i}} }}{{V_{i} }} \hfill \\ = r_{\text{oa}} \cdot \left( {k_{\text{gp}} \phi_{\text{Np}} \phi_{\text{Lp}} a_{\text{p}} - {\text{F}}_{\text{oxp}} \cdot k_{\text{rp}} \cdot a_{\text{p}} } \right) + r_{\text{od}} \left[ {{\text{BotAlgPhoto}} - F_{\text{oxb}} \left( {k_{{{\text{rb}}1}} \cdot a_{\text{b}} - k_{{{\text{rb}}2}} {\text{BotAlgPhoto}}} \right)} \right] \hfill \\ \frac{{A_{{{\text{st}},i}} }}{{V_{i} }} - r_{\text{oc}} \cdot \left( {F_{\text{oxcf}} \cdot k_{\text{dc}} \cdot C_{f} } \right) - r_{\text{oc}} \left( {F_{\text{oxcf}} \cdot k_{\text{dcs}} \cdot C_{\text{s}} } \right) - r_{\text{on}} \left( {F_{\text{oxnd}} k_{\text{n}} n_{\text{a}} } \right) + {\text{Reaeration}} - k_{\text{COD}} \left[ {\text{COD}} \right] - {\text{SOD}}\frac{{A_{{{\text{st}},i}} }}{{V_{i} }} \hfill \\ \end{aligned}$$

(3)

$${\text{Reaeration}} = k_{\text{a}} \left[ {\left( {{\text{e}}^{{{\text{lnO}}_{\text{s}} }} \left( {1 - 0.0001148 \cdot {\text{elev}}} \right) - {\text{O}}} \right)} \right]$$

(4)

$${\text{InOs}} = - 139.3411 + \frac{{1.575701X10^{5} }}{{T_{\text{a}} }} - \frac{{6.642308X10^{7} }}{{T_{\text{a}}^{2} }} + \frac{{1.2438X10^{10} }}{{T_{\text{a}}^{ 3} }} - \frac{{8.621949X10^{11} }}{{T_{\text{a}}^{4} }}$$

(5)

CBODu

$$S_{\text{cs}} = r_{\text{od}} {\text{DetrDiss}} - {\text{SlowChydr}} - {\text{SlowCOxidSlowCHydr}} = k_{\text{hc}} \left( T \right)C_{\text{S}}$$

(6)

$$S_{\text{cf}} = {\text{SlowCHydr}} - {\text{FastCOxid}} - r_{\text{ondn}} {\text{Denitr}} + J_{\text{CH4,d}} \frac{{A_{{{\text{st}},i}} }}{Vi}$$

(7)

$${\text{FastCOxid}} = F_{\text{oxcf}} k_{\text{dc}} \left( T \right)f{\text{SLowCOxid}} = F_{\text{oxcf}} k_{\text{dcs}} \left( T \right)C_{\text{S}}$$

(8)

$$S_{\text{DO}} = r_{\text{na}} \cdot \left( {k_{\text{dp}} \cdot a_{p} } \right) + qN\left( {\frac{{k_{\text{db}} a_{\text{b}} }}{H}} \right) - k_{\text{hn}} \cdot n_{\text{o}} - \frac{{v_{\text{on}} }}{H} \cdot n_{\text{o}}$$

(9)

Nitrogen

$$\begin{aligned} S_{\text{na}} = k_{\text{hn}} \cdot n_{\text{o}} - F_{\text{oxna}} \cdot k_{\text{na}} + r_{\text{na}} \left( {F_{\text{oxp}} k_{\text{rp}} } \right)a_{\text{p}} - r_{\text{na}} P_{\text{ap}} \left( {k_{\text{gp}} \phi_{\text{Np}} \phi_{\text{Lp}} } \right) \hfill \\ a_{\text{p}} + \left[ {J_{{{\text{NH}}_{4} }} - P_{\text{ab}} {\text{BotAlgUptakeN}}\left( {\text{NUpWCfrac}} \right)} \right]\frac{{A_{{{\text{st}},i}} }}{{V_{i} }} \hfill \\ \end{aligned}$$

(10)

$$P_{\text{ap}} = \frac{{n_{\text{a}} n_{\text{n}} }}{{\left( {k_{\text{hnxp}} + n_{\text{a}} } \right)\left( {k_{\text{hnxp}} + n_{\text{n}} } \right)}} + \frac{{n_{\text{a}} k_{\text{hnxp}} }}{{\left( {n_{\text{a}} + n_{\text{b}} } \right)\left( {k_{\text{hnxp}} + n_{\text{n}} } \right)}}$$

(11)

$$P_{\text{ab}} = \frac{{n_{\text{a}} n_{\text{n}} }}{{\left( {k_{\text{hnxb}} + n_{\text{a}} } \right)\left( {k_{\text{hnxb}} + n_{\text{n}} } \right)}} + \frac{{n_{\text{a}} b}}{{\left( {n_{\text{a}} + n_{\text{b}} } \right)\left( {k_{\text{hnxb}} + n_{\text{n}} } \right)}}$$

(12)

$$\begin{aligned} S_{\text{nn}} = F_{\text{oxna}} \cdot k_{\text{mn}} \cdot n_{\text{a}} - \left( {1 - F_{\text{oxdn}} } \right)k_{\text{dn}} n_{\text{n}} - r_{\text{na}} \left( {1 - P_{\text{ap}} } \right) \cdot \left( {k_{\text{gp}} \phi_{\text{Np}} \phi_{\text{Lp}} } \right)a_{\text{p}} \hfill \\ + \left[ {J_{{{\text{NO}}_{3} }} - \left( {1 - P_{\text{ab}} } \right){\text{BotAlgUptakeN}}({\text{NUpWCfrac}})} \right] \hfill \\ \end{aligned}$$

(13)

Notations: Ah = biofilm of attached heterotrophic bacteria in the hyporheic sediment zone; ap = phytoplankton concentration (mgA/m³); ab = bottom algae concentration (gD/m²); A _st,i  = surface area of the reach (m²); BotAlgPhoto = bottom algae photosynthesis (gO₂/m²/day); BotAlgUptakeN = uptake rate for nitrogen in bottom algae (mgN/m²/day); BotAlgUptakeP = uptake rate for phosphorous in bottom algae (mgP/m²/day); BotAlResp = bottom algae respiration (gO₂/m²/day); c_2,i  = concentration in hyporheic sediment zone (mg/L); c _i  = concentration in the surface water in reach i (mg/L); c _i − 1 = concentration in the u/s reach i − 1 (mg/L); CODoxid = oxidation of non-carbonaceous non-nitrogenous chemical oxygen demand (gO₂/m²/day); Denitr = rate of denitrification [mgN/L/day]; E′ _i − 1, E′ _i  = bulk dispersion coefficients between reaches i − 1 and i and i and i + 1 (m³/day), respectively; E′ _hyp,j = bulk dispersion coefficients between hyporheic zone and reach i (m³/day); FastCOxid = fast CBOD oxidation (gO₂/m²/day); F _oxcf = attenuation due to low oxygen [dimensionless]; F _oxna = attenuation due to low oxygen on ammonia nitrification (dimensionless); F _oxp = attenuation due to low oxygen on phytoplankton respiration; H₂,i = the thickness of the hyporheic zone (cm); IN_b = intracellular nitrogen concentration in bottom algae (mgN/m²); IP_b = intracellular phosphorus concentration in bottom algae (mgP/m²); J _CH4,_d = the sediment flux of dissolved methane in oxygen equivalents (gO₂/m²/day); J _NH4 = sediment flux of ammonia (mgN/m²/day); J _NO3 = sediment flux of nitrate (mgN/m²/day); J _PO4 = sediment flux of inorganic P (mgP/m²/day); k _a = reaeration rate (1/day); k _dc(T), k _dcs(T) = temperature-dependent fast CBOD oxidation rate [day]; k _dp = phytoplankton death rate (/day); k _gp = maximum photosynthesis rate at temperature (day); k _hc(T) = temperature-dependent slow CBOD hydrolysis rate [day]; k _hn = organic nitrogen hydrolysis rate (1/day); k _hnxb = preference coefficient of bottom algae for ammonium (mgN/m³); k _hnxp = preference coefficient of phytoplankton for ammonium (mgN/m³); k _na = nitrification rate for ammonia nitrogen (1/day); k _nn = temperature-dependent nitrification rate for ammonia nitrogen (1/day); k _rp = phytoplankton respiration rate (1/day); NH₄nitr = ammonium nitrification (gO₂/m²/day); NUpWCfrac = fraction of N uptake from the water column by bottom plants; Os = saturation concentration of dissolved oxygen (mgO₂/L); P _ab = preferences for ammonium as a nitrogen source for bottom algae; P _ap = preferences for ammonium as a nitrogen source for phytoplankton; Phytophoto = phytoplankton photosynthesis (gO₂/m²/day); PhytoResp = Phytoplankton respiration (gO₂/m²/day); PUpWCfrac = fraction of P uptake from the water column by bottom plants; Q _ab,i  = total flow abstractions from the reach I; Q _i  = outflow from reach i; Q _i−1 = inflow from the u/s reach i − 1; qN = actual cell quotas of nitrogen (mgN/gD); qP = actual cell quotas of phosphorous (mgP/gD); Reaeration = (gO₂/m²/day); r _na = ratio of nitrogen to chlorophyll a (mgN/mgA); r _od = ratio of oxygen consumed to detritus (mgO₂/mgD) during bottom algae respiration; r _on = ratio of oxygen consumed to nitrogen during nitrification (mgO₂/mgN); r _oa = ratio of oxygen generated to phytoplankton growth (mgO₂/mgA); r _oc = ratio of oxygen consumed during CBOD oxidation (mgO₂/mgO₂); rpa = ratio of phosphorus to chlorophyll a (mgP/mgA); S ₂,i = sources and sinks of the constituent in the hyporheic sediment zone due to reactions; S _ah,i  = sources and sinks of heterotrophic bacteria in the hyporheic sediment zone due to reactions (gD/m²/days); S _b,i  = sources and sinks of bottom algae biomass due to reactions (gD/m²/day); S _bN,i  = sources and sinks of bottom algae nitrogen due to reactions (mgN/m²/day); S _bP,i  = sources and sinks of bottom algae phosphorus due to reactions (mgP/m²/day); S _i  = sources and sinks of constituent i due to reactions and mass transfers (mg/L/day); SlowCOxid = slow CBOD oxidation (gO₂/m²/day); T _a = absolute temperature (°K), elev = elevation of the area (m); V₂,i = (Φs,iA_st, _i H₂,i/100) volume of pore water in the hyporheic sediment zone (m³); V _i  = volumes of reach i (m³), t = time (day); v _i  = inorganic suspended solids’ settling velocity (m/day); W _i  = external loading of the constituent to reach i (mg/day); Φ_Lp = phytoplankton light attenuation factor (dimensionless); Φ_Np = phytoplankton nutrient attenuation factor (dimensionless); and Φs,i = porosity of the hyporheic sediment zone.

Assumptions and limitations

The flow is assumed to be in a steady state. The model simulates only the main stem of a river and does not simulate branches of the river system. It does not presently include an uncertainty component.

Point source pollution inventory

The model has been calibrated for four monitoring stations M1–M4. Thirteen wastewater drains, namely Najafgarh, Magazine Road, Sweeper Colony, Khyber Pass, Metcalf House, ISBT+ Mori Gate, Tonga Stand, Civil Mill, drain No 14, Power House, Sen Nursing Home, Barapulla, and Maharani Bagh, and a tributary (named Hindon cut) carrying domestic sewage have been considered in the study. Abstraction of water from the study stretch occurs at Wazirabad barrage and 39 km D/S Palla via Agra canal (Fig. 1). The river has been divided into 17 reaches with 21 sub-reaches starting from Palla (headwater point) and ending at Okhla (Ending point) along with the two abstraction points—one at Wazirabad barrage and another at Agra canal (Fig. 1). The river segmentation is based on making divisions at points of major changes, such as confluence with major tributaries or drains. QUAL2Kw is not constrained to uniform reach sizes, and therefore variable reach sizes have been selected as appropriate based on major changes such as locations of large inflows and outflows. Hindon cut is also observed to be one of the major contributors to the flow and BOD load to the river. Figure 1 shows a schematic diagram of the study area. The figure illustrates the flow profile of river Yamuna with various dams, reservoirs, abstractions, and drains up to Delhi.

The data have been collected during October 1999–June 2009 for pH, DO, BOD, nitrogenous compounds, TC, COD, alkalinity, temperature, and electrical conductivity (CPCB 2000, 2007; and personal communications with CPCB, CWC, and DJB, Sharma 2013). Similarly, the monthly average river quality data for all the years have been collected from both CPCB and CWC. The river discharge data have been collected from CWC, and the point source discharge data have been collected from CPCB and SPCB (CPCB 2000, 2007, and personal communications with CPCB and SPCB, Sharma 2013).

Table 1 shows reach-wise decadal average of the flow of point abstraction, point inflow, length, width, depth, and velocity. The table gives the decadal average characteristics of the entire river reach. The details of M1, D1–D13, T1, and A1–A2 are given. The table shows that the river is not very deep in the entire study area, except where D11 is meeting the river. It can also be seen that the velocity in the river is very low ranging from 0.04 to 0.22 m/s. A1 shows that most of the water is being withdrawn from this location and whatever the river carries d/s A1 is the wastewater from D1 to D13 and T-1.

Table 1 Decadal average characteristics of various pollution loads and withdrawals

In 1958, O’Connor and Dobbins gave the stream reaeration equation for a slow-moving stream, such as Yamuna, with depth less than 1 m (PDER, 1981). Therefore, for the present study, reaeration has been calculated using O’Connor and Dobbins’ equation. In the present model, SOD is relatively small because of DO depletion as compared to BOD, COD, and nitrification. According to Chapra (1997), the SOD for organic river sediments lies within a range of 1–2 g/m²/d; therefore, for the present study, the bottom SOD coverage has been assumed to be 100 % and the prescribed SOD (gO2/m²/day) is taken as 1.0 (Thomann 1972; Rast and Lee 1978). The sediment/hyporheic zone thickness, sediment porosity, and hyporheic exchange flow have been taken as 10 cm, 0.4, and 0 %, respectively (Kannel et al. 2007). Numerous global rate parameters, which define and simulate the model, are calibrated to obtain the best fitness while comparing the observed data and the model predictions.

Input Data

BOD, DO, nitrogen and its compounds, and TC were modeled. All BOD, TN, and TC negatively impact the DO levels in a river. The data were collected from various government agencies including Central Pollution Control Board (CPCB 2007) and Central Water Commission (CWC) for pH, DO, BOD, nitrogenous compounds, TC, COD, alkalinity, river water temperature, and EC (CPCB 2007; Central Water Commission, Communication for Doctoral Research 2009; CPCB 2011). In the present study, it has been assumed that COD represents the total oxygen demand including ultimate carbonaceous BOD (CBODu) and the CBODf only represents a portion of the total that reacts most quickly. Therefore, the remaining portion is represented slower reacting oxygen demand which in QUAL2Kw is labeled as CBODs. The BOD5 method (Standard methods for the examination of water and wastewater, 20th edn 1998) does not measure total oxygen demand. Therefore, the CBODs represents the remaining oxygen demand that is not represented by the BOD test (Standard methods for examination of water and wastewater 1998; Clair 2003). Finally, BOD has been taken as CBODf and CBODs is calculated by deducting CBODf from COD. The values of organic nitrogen, ammonia nitrogen, and nitrate-nitrogen were obtained from Total Kjeldahl Nitrogen (TKN), ammonia, and nitrate after following conversions (ref).

The organic nitrogen (in µg/l) is measured as ${\text{ON}} = \left[ {{\text{TKN}} - \left( {\frac{\text{Ammonia}}{1.3}} \right)} \right] \times 1000.$ The ammonia–nitrogen (in µg/l) is measured as ${\text{NH}}_{4} - {\text{N}} = \left[ {\frac{\text{Ammonia}}{1.3}} \right] \times 1000.$ The nitrate-nitrogen (in µg/l) is measured as ${\text{NO}}_{3} - {\text{N}} = \left[ {\frac{\text{Nitrate}}{4.4}} \right] \times 1000.$

Air temperature, dew temperature, wind speed, cloud cover, and shade for the study period were obtained from India Meteorological Department (IMD) and CWC. The monthly average parameters have been taken for the study area. The data for velocity, depth, and width have been collected from DJB and CWC for 2008 and 2009. Thereafter, the hydraulic characteristics have been calculated, and the values for hydraulic coefficients and exponents were calculated using linear regression method (Eqs. 14–16):

$$V \, = {\text{ a}}Q^{\text{b}}$$

(14)

$$h \, = {\text{ c}}Q^{\text{d}}$$

(15)

$$w \, = {\text{ e}}Q^{\text{f}}$$

(16)

$${\text{a }} \times {\text{ c }} \times {\text{ e }} = { 1}$$

$${\text{b }} + {\text{ d }} + {\text{ f }} = { 1},$$

where V is the average velocity of the river reach under consideration; Q is the discharge; h is the average depth of the river reach under consideration; w is the average width of the river reach under consideration; a, c, and e are the velocity, depth, and width coefficients, respectively; b, d, and f are the velocity, depth, and width exponents, respectively. These values are in conformity with the previous studies (Paliwal et al. 2007; Parmar and Keshari 2011; Central Water Commission, Communication for Doctoral Research 2009, official communication; CPCB 1982–1983; Ghosh 1996; Chapra 1997; DJB 2005). These values are considered to be constant for the entire period of analysis. According to Chapra (1997), SOD for organic river sediments lies within range of 1–2 g/m²/day, and therefore for the present study the bottom SOD coverage has been assumed to be 100 % and the prescribed SOD (g O₂/m²/day) is taken as 1.0 (Thomann 1972; Rast 1978). The sediment/hyporheic zone thickness, sediment porosity, and hyporheic exchange flow have been taken as 10 cm, 0.4, and 0 %, respectively (Kannel et al. 2007).

Global values for rate parameters have been used and calibrated. The rate parameters considered for the study are—slow CBOD: hydrolysis rate and oxidation rate; fast CBOD: oxidation rate; organic N: hydrolysis and settling velocity; ammonium: nitrification; nitrate: denitrification and sed denitrification transfer coeff; and pathogens: decay rate and settling velocity. The model is calibrated using first 45-month data (October 1999–June 2004) and validated using next 45-month data (October 2004–June 2009), using rates obtained from the calibrated model. To avoid instability, the model has been calibrated with a calculation time step of 5.625 min. The time taken for the total discharge to pass through the study area is higher for February and November as compared to other months. The Euler method (Brent method for pH modeling) (Chapra et al. 2007) has been applied for numerical integration, and the simulation has been integrated for different time periods depending upon the month, which is calibrated and validated. For calibration purpose, the years have been divided into three categories, namely January–February, March–June, and October–December. The goodness of fit has been performed wherein equal weights have been assigned to various parameters, so as to minimize the error between observed and simulated values. These values have been obtained using various trials considering rate parameters and default values in the model. The population, np = 200 with generations, ngen = 100 has been used for GA resulting in the generation of a total of 20 001 different values and out of which the value which gives maximum fitness function has been chosen for the period and kept constant for the validation purpose. DO, CBODf, ammonia, TC, alkalinity, pH, and CBODu have been used for the auto-calibration fitness function. In addition, coefficient of determination (R²) showing goodness of fit, mean bias error (MBE), standard deviation bias error (SDBE), root mean square error (RMSE), and normalized RMSE have also been calculated for analyzing statistical variations among observed and predicted values.

Tables 2, 3, 4, 5, 6, 7, and 8 show the average input data required for the model. The data have been segregated on the basis of the three periods, namely January–February, March–June, and October–December. Table 2 gives the input water quality and discharge data for the headwater point, which in this study is M1 (i.e., Palla). The HW flow is found to be the highest during the period of October–December as compared to the other two. The concentration of TC is maximum and DO is minimum during March–June. Table 3 gives the coefficients and exponents of velocity and depth calculated for the entire river reach along with the reach’s name, number, and length. These coefficients and exponents vary seasonally.

Table 2 Headwater Input Data

Table 3 Reach Input Data

Table 4 Prescribed Aeration (per day)

Table 5 Light and heat parameters

Table 6 Point source water quality

Table 7 Rates

Table 8 Water quality input file

Table 4 gives the average reach-wise aeration. The reaeration values have been calibrated using O’Connor and Dobbins’ equation in the model. The air temperature is the highest during the March–June period, which is a summer season. It gets low during October–December and becomes minimal in January–February. The air temperature impacts the water temperature, which finally affects the water quality of the river. Similarly, the dew point temperature is maximum during March–June and minimum during January–February. The wind speed is observed to be maximum during March–June and minimum during October–December periods. The percentage of cloud cover over the study area is the highest during January–February, lesser during March–June, and the lowest during October–December seasons.

Table 5 gives the light and heat rate parameters used for the study region. These parameters have been kept constant throughout the study period. They have been taken from the global rate parameters (Chapra et al. 2007). Table 6 provides the water quality input data used for the study. The reach-wise data are given on all the input parameters used for the study. The DO for all the point sources (D1–D13) is “zero” except for T1 and A2. The maximum wastewater flow is being added by D1, and the maximum BOD concentration is being added by D2, D8, and D13. A huge amount of TC is being added by all the input point sources. The drains have high ON loadings. Table 7 gives details of the global rates being used for the water quality parameters under study. The values with “Yes” Auto-cal option have been calibrated using GA mode of the QUAL2Kw model. This has been done for all the periods as they keep on varying depending upon the discharge and concentrations of various water quality constituents under study. Table 8 details the water quality data for M1–M4 used as inputs for the model. These data are required to calibrate and validate the model for simulated and observed water quality variables. The observed flow at M1 is the river discharge, whereas at M2 it is mainly due to the addition of wastewater drains.

The observed dataset shows little temperature variation among the monitoring stations, which is again maximum during summer and minimum during January–February period of the study. Table 8 shows that DO is less than 1 mg/l at all the monitoring stations except for M1. The TC, BOD, and TN are quite high at M2–M4 as compared to M1. However, TC is not meeting the desired standard even at M1.

Sensitivity analysis data inventory

The errors associated with the variations in parameters have been quantified using sensitivity analysis, which also helps in evaluating the robustness of a model. The sensitivity analysis has been done to identify the parameters having maximum influence on the DO, CBODf, TC, and total nitrogen (TN) output. The critical parameters are affected by the amount of flow, nitrogenous compounds, BOD, and TC in the river system. Therefore, for sensitivity analysis, the variations in CBODf oxidation rate, ammonia nitrification rate, pathogen decay rate, headwater (HW) flow, point source flow, point source CBODf, reaeration rate, point source pathogen, and point source TN have been studied. The analysis has been done keeping all the parameters constant excepting the parameter that was being tested during the calibration. The parameter to be tested has been decreased and increased by 20 %, and the corresponding responses in DO, CBODf, TC, and TN have been compared with the simulated water quality.

Uncertainty analysis data inventory

Modeling a river experiences varied and inescapable irregularities in data collection resulting in making the assumptions in the model parameters leading to the magnification of the errors in the model outputs. The reliability of a model as a predictive tool and the relationship among the input and output values of a model can be obtained by performing uncertainty analysis. In this study, the MCS has been done for the three time periods, namely January–February, March–June, and October–December, to understand the effect of input variables on DO, BOD, TC, and TN. In total, 131 parameters have been chosen, which include discharge, DO, CBODf, temperature, TC, ON, and NH4-N from both HW and point sources; reach-wise reaeration rates; CBODf oxidation rate, hydrolysis rate, and settling velocity rate of ON; nitrification and denitrification rates; and decay rate and settling velocity rates for pathogens. To obtain a reasonable estimate, 1000 MCSs have been made, using YASAIw software (Pelletier 2009)—a program which is capable of integrating into QUAL2Kw and runs an MCS.

The uncertainty analysis is conducted by running the QUAL2Kw model in a loop that repeats a specified number of times. Each time the model run is repeated, the program generates a new set of randomly varied input variables. The program records the input values and output values at the end of each run and then repeats the process. At the end of the uncertainty analysis, the model can output histograms and probability density functions for each output variable.

Results and discussion

Evaluation of QUAL2Kw model for its applicability in the study stretch

Evaluation of the model includes calibration, validation sensitivity, and uncertainty analysis to establish its reliability for intervention analysis.

Model calibration and validation

The summary of calibrated and validated values is given in Fig. 2 and Table 9. The figure gives the results showing simulated and observed pollutant characteristics for both model calibration and validation for the entire study stretch. When optimised by GA method, the results show good agreement between the observed and simulated water quality at all the locations (Fig. 2). Total nitrogen (TN) is estimated by adding all the nitrogenous compounds, including as ON, NH₄N, and nitrate-nitrite-nitrogen.

Fig. 2

Calibration and validation

Table 9 Descriptive statistics for model calibration and validation

The predicted value of the model is compared with the observed values using statistical methods to test the applicability of the model for the study stretch. Figure 2 shows the results for calibrated and validated values for DO, CBODf, TN, and TC.

The R² is observed to be least in DO for all the periods and at all the monitoring stations. The reason for low DO values could be attributed to the fact that the respiration via phytoplanktons has not been considered in the study. A very good R² is noted for simulated and observed dataset for TC at all monitoring stations and for all study periods. The R² for CBODf and TN lies within the range of 0.53–0.75 and 0.68–0.83, respectively. This shows that the model has given satisfactory results in terms of R² for CBODf, TN, and TC.

In calibrated model, the mean bias error (MBE) range for DO, CBODf, TN, and TC are −0.42 to −0.17, −3.34 to 0.38, −1.64 to −0.9, and −7563.54 to −775.83 and RMSE ranges are 0.41–0.92, 0.61–8.4, 2.5–5.09, and 2445–22210.13, respectively. Whereas in the validated results, the mean bias range for DO, CBODf, TN, and TC are noted as −0.12 to -0.06, −3.33 to 1.51, 0.61 to 1.2, and −402.08 to 359.46 and RMSE ranges are observed to be in range of 0.13 to 0.27, 4.88 to 9.23, 3.03 to 3.96, and 2043.32 to 6292.18, respectively.

The low range of MBE for DO, CBODf, and TN shows that the correspondence of degree between the mean forecast and mean observation is satisfactory. However, for TC the values are again very low, indicating that the values have been under-forecasted as compared to the observed values. The results obtained from SDBE are in confirmation with the MBE results.

The high range of RMSE observed for TC quantifies the gap existing between the observed and predicted values for M2–M4 monitoring stations. Normalized RMSE is the highest for DO and less for other variables.

When compared, it is observed that the ranges for the statistical indicators used for the study are similar for all the stations and respective variables. The results show that the model gives satisfactory R² for all the parameters except DO. However, the results obtained from other statistical indicators, including RMSE, MBE, and SDBE, show that the difference between observed and simulated DO values is low, indicating satisfactory results. The results also show that statistically QUAL2Kw model is able to explain the relationship between observed and simulated parameters for all the three locations. The results, when compared to the previous studies (Paliwal et al. 2007; Parmar and Keshari 2012), show that the model is able to simulate the extensive dataset with minimal errors. However, to further quantify the errors, sensitivity and uncertainty analysis has been done.

Sensitivity analysis

The results of the sensitivity analysis are presented in Fig. 3, where it is seen that the DO model is highly sensitive to CBODf oxidation rate, ammonia nitrification rate, HW flow, and reaeration rate. It is observed that CBODf concentrations are highly sensitive to CBODf oxidation rate, HW flow, point source flow, point source CBODf, and point source TN. The TN concentration is primarily affected by ammonia nitrification rate, HW flow, point source flow, and point source TN, whereas TC concentrations are impacted by pathogen decay rate, HW flow, point source flow, and point source pathogen. The sensitivity results for DO–BOD are in conformity with the previous studies done by Ahsan (2004), Paliwal et al. (2007), and Parmar and Keshari (2012).

Fig. 3

Sensitivity Analysis for DO, CBODf, TN, and TC

Uncertainty analysis

MCS is a method for numerically operating a complex system having random components. In this method, the input variables are sampled at random from predetermined probability distribution with or without correlation. The distribution of output values generated from repeated simulations is analyzed statistically.

The results suggested that input data efficiently simulated conditions prevailing in the river system. The frequency histograms and cumulative percentage for each output variable are shown in Figs. 4, 5, and 6. The figures give the period-wise uncertainty graphs for CBODf_max, CBODf_min, TC_max, TC_min, TN_max, and TN_min. It is observed that for all the three periods, there is no/negligible DO in the river and, therefore, no MCS output has been generated for the DO at M2, M3, and M4. However, for the rest of the parameters, these locations are characterized by fluctuations in loads and concentrations. The MCS output results for BOD are in accordance with the previous studies done by Paliwal et al. (2007).

Fig. 4

Frequency distribution and cumulative percentage for January–February at M2, M3, and M4

Fig. 5

Frequency distribution and cumulative percentage for March–June at M2, M3, and M4

Fig. 6

Frequency distribution and cumulative percentage for October–December at M2, M3, and M4

The frequency histograms are normally distributed except for the TC_min at M4, which is slightly skewed toward the left. The CBODf is in the range from 10.6 to 39.14 mg/l; TC lies within a range of 110.42–101464 1000 MPN/100 ml; and TN is between 14.68 and 24.55 mg/l. The maximum standard deviation is observed in the case of TC. The results are in accordance with the modeling and sensitivity results obtained previously.

The results also suggested that the probability of water quality parameters, namely CBODf, TN, and TC, deviating from the observed values is low. The results show no MCS output for DO, indicating the combined impact of CBOD, nitrogenous compounds, and TC on the DO of the river. QUAL2Kw model is applied in the study stretch and can be used for intervention analysis for DO, CBODf, TN, and TC.

Conclusions

The QUAL2Kw has been tested and validated at various observed locations in Delhi using a decadal dataset, which includes the outcomes of both YAP I and II in terms of water quality parameters. In addition to the CBODf, the effect of nitrogenous compounds and TC has also been simulated. The sensitivity and uncertainty analysis is used to identify the model parameters, which greatly affect the model output. They also define the water quality variables that should be simulated for model calibration. The CBODf oxidation rate, ammonia nitrification rate, HW flow, and reaeration rate are found to have a maximum impact on the DO of the river. Rest of the parameters, including point source characteristics, do have an impact on other variables but no impact on the DO, indicating that the river is highly polluted and there is an urgent need to minimize the pollutant level of more than 20 % in the river.

The performance of QUAL2Kw model used for river quality modeling has been evaluated based on the monthly predicted and observed values of DO, CBODf, TN, and TC at four CPCB and CWC monitoring stations spread over Delhi. The model performance indices, viz. R², RMSE, MBE, SDBE, and normalized RMSE, indicates that the performance of QUAL2Kw model is satisfactory for DO, BOD, TC, and TN for all the monitoring stations. The results are in conformity with the previous studies done by Paliwal et al. (2007), Kannel et al. (2007), Xiaobo et al. (2008), and Parmar and Keshari (2012). The model can simulate parametric speciation for BOD and nitrogenous compounds. The sensitivity and uncertainty components of the model have been evaluated and considered prior to applying the model for the interventions. The results show that the calibrated and validated model can be applied successfully to generate the future scenarios for the study area.

The study has contributed a comprehensive inventory of a number of possible river-polluting sources with the objective of conducting source apportionment in Delhi. Earlier studies (Bhargava 1983, 1986; Kazmi and Hansen 1997; Kazmi 2000; Ahsan 2004; Kazmi and Agrawal 2005; Kazmi et al. 2007; Paliwal et al. 2007; Sharma and Singh 2009; Parmar and Keshari 2012) have reported the river quality based on DO and BOD only and have not included other vital parameters like coliforms and nitrogenous compounds, which also directly impact the river’s DO. These parameters have been included in the present research.

The results of this research show that it is possible to formulate and evaluate the regulatory intervention related to the river pollution control in developing countries like India using WQMs. In India, detailed environmental modeling tools are rarely used prior to the development of an RQRP. The outcome of all these analyses can be used by policy makers for planning RQRPs.