Skip to main content
SpringerLink
Log in

Solving intuitionistic fuzzy transportation problem using linear programming

  • Original Article
  • Published:
International Journal of System Assurance Engineering and Management Aims and scope Submit manuscript

Abstract

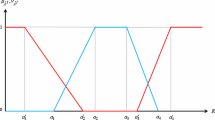
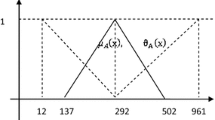
The real life transportation problems (TP) face a lot of problems due to uncertainties and lack of precise data. The present paper focuses on the two methods for solving intuitionistic fuzzy TP. One of the methods uses intuitionistic fuzzy programming technique together with the three different membership functions—linear, exponential and hyperbolic and the other method uses crisp linear programming taking intuitionistic fuzzy data in both the methods for the cost objective functions in the TP. The first method uses the membership and non-membership degrees separately to find the crisp solution using the fuzzy programming technique and then the optimal solution is calculated in terms of intuitionistic fuzzy data with the help of defined cost membership functions using the different membership functions. The satisfaction degree is then calculated to check the better solution. The second method directly solves the TP to find crisp solution considering a single objective function. The cost objective function is taken as intuitionistic fuzzy data and the methods have been used as such for the first time. A large scale real life intuitionistic TP has been solved using the two methods. The results obtained for different membership functions have been compared.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Aggarwal S, Gupta C (2014) Algorithm for solving intuitionistic fuzzy transportation problem with generalized trapezoidal intuitionistic fuzzy number via new ranking method. export.arxiv.org, 01/2014, Source: arXiv

  • Angelov PP (1997) Optimization in an intuitionistic fuzzy environment. Fuzzy Sets Syst 86:299–306

    Article  MATH  MathSciNet  Google Scholar 

  • Antony RJP, Savarimuthu SJ, Pathinathan T (2014) Method for solving the transportation problem using triangular intuitionistic fuzzy number. Int J Comput Algorithm 03:590–605

    Google Scholar 

  • Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96

    Article  MATH  Google Scholar 

  • Bit AK, Biswal MP, Alam SS (1992) Fuzzy programming approach to multicriteria decision making transportation problem. Fuzzy Sets Syst 50:135–141

    Article  MATH  MathSciNet  Google Scholar 

  • Bit AK, Biswal MP, Alam SS (1993) An additive fuzzy programming model for multi-objective transportation problem. Fuzzy Sets Syst 57:313–319

    Article  MATH  Google Scholar 

  • Cao B (1992) Transportation problem with nonlinear side constraints: a branch and bound approach. ZOR Methods Models Oper Res 36(2):185–197. doi:10.1007/BF01417216

    Article  MATH  MathSciNet  Google Scholar 

  • Chanas S, Kuchta D (1996) A concept of the optimal solution of the transportation problem with fuzzy cost coefficients. Fuzzy Sets Syst 82:299–305

    Article  MathSciNet  Google Scholar 

  • Chanas S, Kuchta D (1998) Fuzzy integer transportation problem. Fuzzy Sets Syst 98:291–298

    Article  MATH  MathSciNet  Google Scholar 

  • Chanas S, Kolodziejczyk W, Machaj A (1984) A fuzzy approach to the transportation problem. Sets Syst 13:211–221

    Article  MATH  MathSciNet  Google Scholar 

  • Kaur D, Mukherjee S, Basu K (2011) Multi-objective multi-index real life transportation problem with crisp objective function and interval valued supply and destination parameters. In: Proceedings of international conference on mathematical and computational models, (ICMCM’ 2011), Dec 19–21 2011, computational and mathematical modeling, pp 284–291, PSG College of Technology, Coimbatore, ISBN: 978-81-8487-1647

  • Kaur D, Mukherjee S, Basu K (2012a) Multi-objective multi-index real life transportation problem with interval valued parameters. In: Proceedings of the national seminar on recent advances in mathematics and its applications in engineering sciences (RAMAES 2012), March 16–17 2012, Bengal College of Engineering and Technology, Durgapur, pp 29–36, ISBN: 978-93-5067-395-9

  • Kaur D, Mukherjee S, Basu K (2012b) Goal programming approach to multi-index real life transportation problem with crisp objective function and interval valued supply and destination parameters. In: Proceedings of international conference on optimization, computing and business analytics (ICOCBA 2012), December 20–22 2012, pp 30–36, ISBN: 978-81-8424-8142

  • Kaur D, Mukherjee S, Basu K (2013) Solution of a multi-index real life transportation problem by fuzzy non-linear goal programming. In: Proceedings to RAMA-2013, Feb 14–16 2013, ISM, Dhanbad, pp 148–158, ISBN: 978-81-8424-821-0

  • Kaur D, Mukherjee S, Basu K (2015) Solution of a multi-objective and multi-index real life transportation problem using different fuzzy membership functions. J Optim Theory Appl 164(2):666–678

    Article  MATH  MathSciNet  Google Scholar 

  • Dangalchev CA (1996) Partially-linear transportation problems. Eur J Oper Res 91(3):623–633. doi:10.1016/0377-2217(94)00367-X

    Article  MATH  Google Scholar 

  • Dangalchev CA (2000) Optimization of the transportation expense of a firm with contractual supplies. Transp Res Part B Methodol 34(3):203–217. doi:10.1016/S0191-2615(99)00021-1

    Article  Google Scholar 

  • Das SK, Goswami A, Alam SS (1997) Multiobjective transportation problem with interval cost, source and destination parameters. Eur J Oper Res 117(1):100–112

    Article  MATH  Google Scholar 

  • Dorigo M, Maniezzo V, Colorni A (1996) The ant system optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybernet Part B Cybernet 26(1):29–41. doi:10.1109/3477.484436

    Article  Google Scholar 

  • Gani AN, Abbas S (2013) A new method for solving intuitionistic fuzzy transportation problem. Appl Math Sci 7(28):1357–1365

    Google Scholar 

  • Gao C, Yan C, Zhang Z, Hu Y, Mahadevan S, Deng Y (2014) An amoeboid algorithm for solving linear transportation problem. Phys A Stat Mech Appl 398:179–186

    Article  MathSciNet  Google Scholar 

  • Glover F (1977) Heuristic for integer programming using surrogate constraints. Decis Sci 8(1):156–166. doi:10.1111/j.1540-5915.1977.tb01074.x

    Article  Google Scholar 

  • Hitchcock FL (1941) The distribution of a product from several sources to numerous localities. J Math Phys 20:224–230

    Article  MATH  MathSciNet  Google Scholar 

  • Holland JH (1975) Adaptation in natural and artificial systems: monograph. University of Michigan Press, Ann Arbor, p 183

    Google Scholar 

  • Hussain RJ, Kumar PS (2012) Algorithmic approach for solving intuitionistic fuzzy transportation problem. Appl Math Sci 6(80):3981–3989

    MATH  MathSciNet  Google Scholar 

  • Kennedy J, Eberhart R (1995) Particle swarm optimization. In: 1995 IEEE international conference on neural networks proceedings, 1942–1948

  • Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimiza-optimization by simulated annealing. Science 220(4598):671–680. doi:10.1126/science.220.4598.671

    Article  MATH  MathSciNet  Google Scholar 

  • Kuno T, Utsunomiya T (2000) A Lagrangian based branch-and-bound algorithm for production-transportation problems. J Global Optim 18(1):59–73. doi:10.1023/A:1008373329033

    Article  MATH  MathSciNet  Google Scholar 

  • Li L, Lai KK (2000) A fuzzy approach to the multiobjective transportation problem. Comput Oper Res 27(1):43–57

    Article  MATH  MathSciNet  Google Scholar 

  • Nagai H, Kuno T (2005) A simplicial branch-and-bound algorithm for production-transportation problems with inseparable concave production cost. J Oper Res Soc Jpn 48(2):97–100

    Article  MATH  MathSciNet  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets, Inform. Control 8:338–353

    Article  MATH  MathSciNet  Google Scholar 

  • Zhang Y et al (2013) A biologically inspired solution for fuzzy shortest path problems. Appl Soft Comput 13(5):2356–2363

    Article  Google Scholar 

  • Zhang X et al (2014) A biologically inspired optimization algorithm for solving fuzzy shortest path problems with mixed fuzzy arc lengths. J Optim Theory Appl 163(3):1049–1056

    Article  MATH  MathSciNet  Google Scholar 

  • Zhang X et al (2016) A physarum-inspired approach to supply chain network design. Sci China Inf Sci 59:1–14

    MathSciNet  Google Scholar 

  • Zimmermann HJ (1978) Fuzzy linear programming with several objective functions. Fuzzy Sets Syst 1:46–55

    Article  MathSciNet  Google Scholar 

  • Zmmermann HJ (1976) Description and optimization of fuzzy systems. Int J General Syst 2:209–215

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National Institute of Technology, M.G.Avenue, Durgapur, West Bengal, 713209, India

    Dalbinder Kour & Kajla Basu

  2. Gobinda Prasad Mahavidyalaya, Amarkanan, Bankura, West Bengal, 722133, India

    Sathi Mukherjee

Authors
  1. Dalbinder Kour
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sathi Mukherjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kajla Basu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dalbinder Kour.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kour, D., Mukherjee, S. & Basu, K. Solving intuitionistic fuzzy transportation problem using linear programming. Int J Syst Assur Eng Manag 8 (Suppl 2), 1090–1101 (2017). https://doi.org/10.1007/s13198-017-0575-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13198-017-0575-y

Keywords

Mathematical Subject Classification

Search

Navigation