Abstract
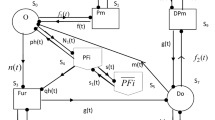
The main concentration of the present study is on the evaluation of some important reliability measures of a single-unit system considering arbitrary distributions for the random variables associated with failure and repair times, time to change of weather conditions, inspection time and arrival time of the server. The system operates under two weather conditions-normal and abnormal. The unit fails completely via partial failure. There is a single server who takes some time to arrive at the system. Server inspects the unit at its complete failure to see the feasibility of its repair while repair of the unit at partial failure is done without inspection. The unit works as new after repair at partial failure whereas unit is assumed as degraded after repair at complete failure. Inspection of the degraded unit is also conducted at its failure to examine the feasibility of repair. The degraded unit is replaced by new one if inspection reveals that its repair is not feasible to the system. Some measures of system effectiveness are obtained using semi-Markov and regenerative point technique. Giving particular values to various parameters and costs, the numerical results for mean time to system failure, availability and profit function are obtained considering exponential and Rayleigh distributions for all random variables.

Similar content being viewed by others
Abbreviations
- E:
-
Set of regenerative states
- N0/D0 :
-
The unit is operative in Normal/Degraded mode
- p1/q1 :
-
Probability that repair of degraded unit is feasible/not feasible
- p2/q2 :
-
Probability that repair of complete failed unit is feasible/not feasible
- Pur/Pwr :
-
Unit is partially failed and under repair/waiting for repair
- Fui/Fwi/Fur/Fwr :
-
Unit is completely failed and under inspection/waiting for inspection/under repair/waiting for repair
- DFui/DFwi/DFur/DFwr :
-
Degraded unit is failed and under inspection/waiting for inspection/under repair/waiting for repair
- f1(t)/F1(t), f2(t)/F2(t), f3(t)/F3(t):
-
p.d.f./c.d.f. for failure time distribution of normal unit, partially failed unit, degraded unit
- g(t)/G(t), g1(t)/G1(t) g2(t)/G2(t):
-
p.d.f./c.d.f. for repair time distribution of normal unit after complete failure, partial failure, degraded unit
- w(t)/W(t):
-
p.d.f./c.d.f. for arrival time of the server
- z(t)/Z(t), z1(t)/Z1(t):
-
p.d.f./c.d.f. for time to change of weather conditions form normal to abnormal, abnormal to normal
- h1(t)/H1(t):
-
pdf/cdf for inspection time of the degraded unit
- h2(t)/H2(t):
-
pdf/cdf for inspection time of the complete failed unit
- qij(t)/Qij(t):
-
pdf/cdf for first passage time from regenerative state i to a regenerative state j or to a failed state j without visiting any other regenerative state in (0, t]
- mij :
-
The conditional mean sojourn time in regenerative state Si when system is to make transition into regenerative state Sj. Mathematically, it can be written as \( m_{ij} = E(\mathop T\nolimits_{ij} ) = \int\limits_{0}^{\infty } {td[Q_{ij} (t)] = - q_{ij}^{{ *^{\prime}}} (0)} \), where T ij is the transition time from state Si to Sj Si, Sj ε E
- μ i :
-
The mean Sojourn time in state Si this is given by \( \upmu_{i} = E(\mathop T\nolimits_{i} ) = \int\limits_{0}^{\infty } {P(T_{i} > t)dt = \sum\limits_{j} {m_{ij} } } \), where T i is the sojourn time in state Si
- Mi(t):
-
Probability that the system initially up in the regenerative state Si at time t without passing through any other regenerative state
- Wi(t):
-
Probability that the server is busy at an instant t, given that the system entered into the regenerative state Si at t = 0
- ®/©:
-
Symbol of Laplace Stieltjes Convolution/Laplace convolution
- **|*:
-
Symbols for Laplace Stieltjes Transform (LST)/Laplace transform (LT)
References
Chander S, Bansal RK (2005) Profit analysis of single-unit reliability models with repair at different failures modes. Proc. INCRSE IIT Kharagpur, India, pp 577–587
Malik SC (2008) Reliability modeling and profit analysis of a single-unit system with inspection by a server who appears and disappears randomly. Pure Appl Math Sci LXVII(1–2):135–146
Malik SC, Barak MS (2009) Reliability and economic analysis of a system operating under different weather conditions. J Proc Natl Acad Sci 79(Pt II):205–213
Malik SC, Kadyan MS, Kumar J (2010) Cost-analysis of a system under priority to repair and degradation. Int J Stat Syst 5(1):1–10
Pawar D, Malik SC, Bahl S (2010) Steady state analysis of an operating system with repair at different levels of damages subject to inspection and weather conditions. Int J Agricult Stat Sci 6(1):225–234
Acknowledgments
The authors are thankful to the reviewers for their valuable comments that led to an improved presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kadyan, M.S., Promila & Kumar, J. Reliability modeling of a single-unit system with arbitrary distributions subject to different weather conditions. Int J Syst Assur Eng Manag 5, 313–319 (2014). https://doi.org/10.1007/s13198-013-0168-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-013-0168-3