A New Construction of Covariance Functions for Gaussian Random Fields

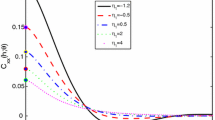
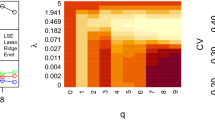
Abstract

We develop a new approach to creating covariance functions for Gaussian random fields via point processes on the complex plane. We present two approaches to construct valid covariance functions by exploiting Bochner’s theorem and then modeling the characteristic function of a covariance function. In particular, we use a complex point process (CPP) to model the Fourier coefficients and illustrate how to estimate the covariance function of a Gaussian random field model from data. We further illustrate our construction approaches and compare several algorithms via simulations. The methods are exemplified via applications to real-life research data in wheat yields and earthquake studies.

Appendix

1.1 Proof of Theorem 2

Proof

Since the covariance function is defined on $r\in [0,+\infty )$, with $\rho (x_1,x_2)=\rho (r)=\rho (||x_1-x_2||)$, condition (2) in Pólya’s condition is automatically satisfied.

When the covariance function and all of the functions $\theta _k(r), k=0,1,2,3,4,5$, are twice continuously differentiable, and we only use a window with $x\ge 0$, the expectation will be convex if

$$\begin{aligned} \frac{\partial ^2}{\partial r^2}E(\hat{\rho }(r))\ge 0, for\; all\; r>0, \end{aligned}$$

(A.1.1)

that is,

$$\begin{aligned} \frac{\partial ^2}{\partial r^2}E(\hat{\rho }(r))=\frac{\partial ^2}{\partial r^2}\int _A\int _B x\exp (\theta _0(r)+\theta _1(r)x+\theta _2(r)y+\theta _3(r)xy+\theta _4(r)x^2+ \theta _5(r)y^2)dxdy \end{aligned}$$

$$\begin{aligned} =\int _A\int _B \frac{\partial ^2}{\partial r^2}x\exp (\theta _0(r)+\theta _1(r)x+ \theta _2(r)y+\theta _3(r)xy+\theta _4(r)x^2+\theta _5(r)y^2)dxdy \end{aligned}$$

$$\begin{aligned} =\int _A\int _Bx\lambda _r(z)(\theta ^{\prime }_0(r)+\theta ^{\prime }_1(r)x+ \theta ^{\prime }_2(r)y+\theta ^{\prime }_3(r)xy+\theta ^{\prime }_4(r)x^2+ \theta ^{\prime }_5(r)y^2)^2dxdy \end{aligned}$$

$$\begin{aligned} +\int _A\int _Bx\lambda _r(z)(\theta ^{\prime \prime }_0(r)+\theta ^{\prime \prime }_1(r)x+\theta ^{\prime \prime }_2(r)y+\theta ^{\prime \prime }_3(r)xy+ \theta ^{\prime \prime }_4(r)x^2+\theta ^{\prime \prime }_5(r)y^2)dxdy, \end{aligned}$$

(A.1.2)

and thus when condition (1) in the theorem holds, this integral is guaranteed to be non-negative, and the expectation is convex.

Note that if

$$\begin{aligned} \theta ^{\prime \prime }_0(r)+\theta ^{\prime \prime }_1(r)x+\theta ^{\prime \prime }_2(r)y+\theta ^{\prime \prime }_3(r)xy+\theta ^{\prime \prime }_4(r)x^2+ \theta ^{\prime \prime }_5(r)y^2\ge 0, \end{aligned}$$

(A.1.3)

for $r\ge 0, x\in A, y\in B$ almost surely, the expectation is convex, since

$$\begin{aligned} (\theta ^{\prime }_0(r)+\theta ^{\prime }_1(r)x+\theta ^{\prime }_2(r)y+\theta ^{\prime }_3(r)xy+\theta ^{\prime }_4(r)x^2+\theta ^{\prime }_5(r)y^2)^2\ge 0. \end{aligned}$$

(A.1.4)

For condition (4) in Pólya’s conditions, we need $\lim _{r\rightarrow \infty }E(\hat{\rho }(r))=0$, which implies that

$$\begin{aligned} \lim _{r\rightarrow \infty }\int _A\int _B x\exp (\theta _0(r)\!+\!\theta _1(r)x\!+\!\theta _2(r)y\!+\!\theta _3(r)xy\!+\!\theta _4(r)x^2\!+\! \theta _5(r)y^2)dxdy\!=\!0, \end{aligned}$$

(A.1.5)

or

$$\begin{aligned} \int _A\int _B\lim _{r\rightarrow \infty }x\exp (\theta _0(r)\!+\!\theta _1(r)x\!+\!\theta _2(r)y\!+\! \theta _3(r)xy\!+\!\theta _4(r)x^2\!+\!\theta _5(r)y^2)dxdy\!=\!0, \end{aligned}$$

(A.1.6)

and therefore when condition (2) in the theorem holds, i.e.,

$$\begin{aligned} \lim _{r\rightarrow \infty }(\theta _0(r)+\theta _1(r)x+\theta _2(r)y+\theta _3(r)xy+ \theta _4(r)x^2+\theta _5(r)y^2)=-\infty , \end{aligned}$$

(A.1.7)

for $x\in A, y\in B$ almost surely, we have

$$\begin{aligned} \lim _{r\rightarrow \infty }E(\hat{\rho }(r))=0, \end{aligned}$$

(A.1.8)

Thus the expectation follows conditions (2), (3), and (4) of Pólya’s conditions and therefore, it is a positive semi-definite function. $\square$