Abstract
A bias reduction to a kernel estimator of the tail index of randomly right-truncated Pareto-type distributions is made. The asymptotic normality of the derived estimator is established by assuming the second-order condition of regular variation. A simulation study is carried out to evaluate the finite sample behavior of the proposed estimator and compare it to those with non-reduced bias. An application to a real dataset of lifetimes of automobile brake pads is done.

Similar content being viewed by others
References
Beirlant, J., Bardoutsos, A., de Wet, T. and Gijbels, I. (2016). Bias reduced tail estimation for censored Pareto type distributions. Statist. Probab. Lett.109, 78–88.
Beirlant, J., Maribe, G. and Verster, A. (2018). Penalized bias reduction in extreme value estimation for censored Pareto-type data, and long-tailed insurance applications. Insurance Math. Econom. 78, 114–122.
Benchaira, S., Meraghni, D. and Necir, A. (2016a). Tail product-limit process for truncated data with application to extreme value index estimation. Extremes19, 219–251.
Benchaira, S., Meraghni, D. and Necir, A. (2016b). Kernel estimation of the tail index of a right-truncated Pareto-type distribution. Statist. Probab. Lett.119, 186–193.
Caeiro, F. and Gomes, M.I. (2015). Threshold selection in extreme value analysis. Chapter In Extreme Value Modeling and Risk Analysis: Methods and Applications (Dipak, D. and Jun, Y.). (pp. 69-87), Chapman-Hall/CRC, ISBN 9781498701297.
Ciuperca, G. and Mercadier, C. (2010). Semi-parametric estimation for heavy tailed distributions. Extremes 13, 55–87.
Csörgő, S., Deheuvels, P. and Mason, D. (1985). Kernel estimates of the tail index of a distribution. Ann. Statist. 13, 1050–1077.
Gardes, L. and Stupfler, G. (2015). Estimating extreme quantiles under random truncation. TEST 24, 207–227.
Groeneboom, P., Lopuhaä, H.P. and de Wolf, P.P. (2003). Kernel-type estimators for the extreme value index. Ann. Statist. 31, 1956–1995.
de Haan, L. and Stadtmüller, U. (1996). Generalized regular variation of second order. J. Australian Math. Soc. (Series A) 61, 381–395.
de Haan, L. and Ferreira, A. (2006). Extreme Value Theory: An Introduction. Springer, Berlin.
He, S. and Yang, G.L. (1998). Estimation of the truncation probability in the random truncation model. Ann. Statist. 26, 1011–1027.
Hill, B.M. (1975). A simple general approach to inference about the tail of a distribution. Ann. Statist. 3, 1163–1174.
Haouas, N., Necir, A. and Brahimi, B. (2019). Estimating the second-order parameter of regular variation and bias reduction in tail index estimation under random truncation. J. Stat. Theory Pract. 13, Paper 7, 33.
Lawless, J.F. (2002). Statistical Models and Methods for Lifetime Data, 2nd edn. Wiley Series in Probability and Statistics, New York.
Neves, C. and Fraga Alves, M.I. (2004). Reiss and Thomas’ automatic selection of the number of extremes. Comput. Statist. Data Anal. 47, 689–704.
Reiss, R.D. and Thomas, M. (2007). Statistical analysis of extreme values with applications to insurance, finance hydrology and other fields, 3rd edn. Birkhäuser, Berlin.
Strzalkowska-Kominiak, E. and Stute, W. (2009). Martingale representations of the Lynden-Bell estimator with applications. Statist. Probab. Lett. 79, 814–820.
Weissman, I. (1978). Estimation of parameters and large quantiles based on the k largest observations. J. Am. Statist. Assoc. 73, 812–815.
Worms, J. and Worms, R. (2016). A Lynden-Bell integral estimator for extremes of randomly truncated data. Statist. Probab. Lett. 109, 106–117.
Woodroofe, M. (1985). Estimating a distribution function with truncated data. Ann. Statist. 13, 163–177.
Acknowledgements
We gratefully acknowledge the insights, suggestions, and queries by anonymous referees. Discussions with Djamel Meraghni are also greatly appreciated.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
• The authors have no relevant financial or non-financial interests to disclose.
• The authors have no competing interests to declare that are relevant to the content of this article.
• All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.
• The authors have no financial or proprietary interests in any material discussed in this article.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: A
A.1: Instrumental Result
Proposition A.1.
Assume that \(\overline {\mathbf {F}}\in \mathcal {R}\mathcal {V}_{2}\left (-1/\gamma _{1};\tau _{1},A_{\mathbf {F}}\right ) \) and K satisfies assumptions \(\left [ A1\right ] -\left [ A4\right ] ,\) then: \(\left (i\right ) \) \(E_{t}\left (\beta \right ) =\eta _{2}+\eta _{3}A_{\mathbf {F}}\left (t\right ) \left (1+o\left (1\right ) \right ) ,\) for β > 0, and for a given twice-differentiable function f : \(\left (ii\right ) \) \(f\left (L_{t,K}\right ) =f\left (\gamma _{1}\right ) +f^{\prime }\left (\gamma _{1}\right ) \eta _{1}A_{\mathbf {F}}\left (t\right ) \left (1+o\left (1\right ) \right ) ,\) where ηi = ηi,K, i = 1, 2, 3 are stated in (1.7) and Section 1.1 respectively. Moreover
where f∗ is as in (1.12), \(E_{t}\left (\beta \right ) :=E_{t,K}\left (\beta \right ) \) and Lt := Lt,K.
Proof 1.
Recall that (1.10), and let us decompose \(E_{t}\left (\beta \right ) \) into the sum of
and
Using the change of variables \(s=x^{-1/\gamma _{1}}\) we readily show that \(E_{t}^{\left (1\right ) }\left (\beta \right ) =\eta _{2},\) for β > 0. Applying Taylor’s expansion to K∗, we may rewrite \(E_{t}^{\left (2\right ) }\left (\beta \right ) \) into the sum of
and
where \(\xi _{t}\left (x\right ) \) is between \(\overline {\mathbf {F}}\left (tx\right ) /\overline {\mathbf {F}}\left (t\right ) \) and \(x^{-1/\gamma _{1}}.\) Since HCode \(\overline {\mathbf {F}}\in \mathcal {R}\mathcal {V}_{2}(-1/\gamma _{1};\tau _{1},\) AF), then making use of Potters inequalities corresponding to the second-order condition of df F, we write
for any 𝜖 > 0, for all x > 1 and for all large t, see for instance Theorem 2.3.9 in de Haan and Ferreira (2006). Using this inequality, we end up with
Once again, using change of variables \(s=x^{-1/\gamma _{1}},\) we show easily that the previous integral equals to η3. In view of assumption \(\left [ A4\right ] ,\) the function \(K^{\prime }\) is bounded, it follows that
Let 𝜖 > 0 so small such that − 1/γ1 + 𝜖 < 0. The Potters inequalities corresponding to the first order condition of regularly varying functions says:
for all x ≥ 1 and for all large t, see for instance Proposition B.1.9, assertion 5 in de Haan and Ferreira (2006). It follows that
Let us write
Subtracting \(x^{-1/\gamma _{1}}\frac {x^{\tau _{1}/\gamma _{1}}-1}{\tau _{1} \gamma _{1}},\) inside the sign of the previous absolute value, and adding the same quantity, then applying inequality (A.1), we may readily show that \(E_{t}^{\left (2,2\right ) }\left (\beta \right ) =o\left (A_{\mathbf {F}}\left (t\right ) \right ) ,\) as \(t\rightarrow \infty ,\) that we omit further details. Thereby \(E_{t}^{\left (2,1\right ) }\left (\beta \right ) =\left (1+o\left (1\right ) \right ) \eta _{3}\) leading to the result of assertion \(\left (ii\right ) .\) To show the second assertion \(\left (ii\right ) ,\) is suffices to use Taylor’s expansion to function f and similar arguments as used to first assertion \(\left (i\right ) ,\) that we omit details. Let us now focus on the third one \(\left (iii\right ) .\) Multiplying, the equation of assertion \(\left (i\right ) \) by \(f\left (\gamma _{1}\right ) ,\) we write
and from assertion \(\left (ii\right ) \) we have \(f\left (\gamma _{1}\right ) =f\left (L_{t}\right ) -\eta _{1}f^{\prime }\left (\gamma _{1}\right ) A_{\mathbf {F}}\left (t\right ) \left (1+o\left (1\right ) \right ) .\) Substituting the previous expression into the first term of the right-side of equation (A.2), yields
which gives
In particular, for f = f∗, we have \(f_{\ast }\left (\gamma _{1}\right ) =\eta _{2},\) it follows that
which gives the third assertion \(\left (iii\right ) .\) The proof of Proposition A.1 is now completed. □
A.2: High Quantile Estimation
An extreme quantile of df F is a value qν defined in terms of the generalized inverse by \(q_{\nu }:=U_{\mathbf {F}}\left (1/\nu \right ) \) for v ↓ 0. In other words, it is an X-value which is sufficiently large so that the probability of exceeding it is very small. Also known as value-at-risk (VaR), this quantity is largely used, as a risk measure, in several fields such as in finance, insurance, hydrology and reliability. For asymptotic needs, we suppose that v is a function of the observed sample size n, denoted by v = vn, and assumed to be much smaller than 1/n. The estimation of high quantiles of heavy-tailed distributions, in the case of complete data, has been extensively studied in the literature (de Haan and Ferreira, 2006, see, for instance,). The well-known Weissman estimator (Weissman, 1978) of high quantile qν adapted to our new tail index estimator \(\widehat {\gamma }_{1,K}^{\ast }\) is given by
where Fn is Woodroofe’s nonparametric estimator of df F, given in Section 1.
Appendix: B
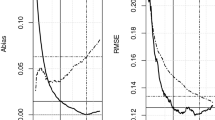
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Burr distribution truncated by another Burr distribution, with β = 1 and γ1 = 0.6 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Burr distribution truncated by another Burr distribution, with β = 0.5 and γ1 = 0.6 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Burr distribution truncated by another Burr distribution, with β = 2 and γ1 = 0.6 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Burr distribution truncated by another Burr distribution, with β = 1 and γ1 = 0.8 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Burr distribution truncated by another Burr distribution, with β = 0.5 and γ1 = 0.8 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Burr distribution truncated by another Burr distribution, with β = 2 and γ1 = 0.8 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Fréchet distribution truncated by another Fréchet distribution, with β = 1 and γ1 = 0.6 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Fréchet distribution truncated by another Fréchet distribution, with β = 0.5 and γ1 = 0.6 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Fréchet distribution truncated by another Fréchet distribution, with β = 2 and γ1 = 0.6 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Fréchet distribution truncated by another Fréchet distribution, with β = 1 and γ1 = 0.8 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Fréchet distribution truncated by another Fréchet distribution, with β = 0.5 and γ1 = 0.8 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Absolute biases (left panel) and RMSE’s (right panel) of \(\widehat {\gamma }_{1,K}^{\ast },\widehat {\gamma }_{1,K},\widehat {\gamma }_{1},\widetilde {\gamma }_{1}^{\ast }\) and \(\overline {\gamma }_{1,K}^{\ast }\) for a Fréchet distribution truncated by a nother Fréchet distribution, with β = 2 and γ1 = 0.8 under the following cases: p = 0.55 (top), p = 0.7 (middle) and p = 0.9 (bottom). The simulation is based on 2000 replicates of size 500
Box-plots corresponding to estimators \(\widehat {\gamma }_{1,K}^{\ast },\) \(\overline {\gamma }_{1,K}^{\ast },\) \(\widetilde {\gamma }_{1}^{\ast },\) \(\widehat {\gamma }_{1,K}\) and \(\widehat {\gamma }_{1}\) for a Fréchet distribution truncated by another Fréchet distribution, with β = 1, γ1 = 0.6, p = 0.55 and p = 0.9 based on 2000 replicates of size N = 500
Box-plots corresponding to estimators \(\widehat {\gamma }_{1,K}^{\ast },\) \(\overline {\gamma }_{1,K}^{\ast },\) \(\widetilde {\gamma }_{1}^{\ast },\) \(\widehat {\gamma }_{1,K}\) and \(\widehat {\gamma }_{1}\) for a Fréchet distribution truncated by another Fréchet distribution, with β = 1, γ1 = 0.8, p = 0.55 and p = 0.9 based on 2000 replicates of size N = 500
Box-plots corresponding to estimators \(\widehat {\gamma }_{1,K}^{\ast },\) \(\overline {\gamma }_{1,K}^{\ast },\) \(\widetilde {\gamma }_{1}^{\ast },\) \(\widehat {\gamma }_{1,K}\) and \(\widehat {\gamma }_{1}\) for a Burr distribution truncated by another Burr distribution, with β = 1, γ1 = 0.6, p = 0.55 and p = 0.9 based on 2000 replicates of size N = 500
Box-plots corresponding to estimators \(\widehat {\gamma }_{1,K}^{\ast },\) \(\overline {\gamma }_{1,K}^{\ast },\) \(\widetilde {\gamma }_{1}^{\ast },\) \(\widehat {\gamma }_{1,K}\) and \(\widehat {\gamma }_{1}\) for a Burr distribution truncated by another Burr distribution, with β = 1, γ1 = 0.8, p = 0.55 and p = 0.9 based on 2000 replicates of size N = 500
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Mancer, S., Necir, A. & Benchaira, S. Bias Reduction in Kernel Tail Index Estimation for Randomly Truncated Pareto-Type Data. Sankhya A 85, 1510–1547 (2023). https://doi.org/10.1007/s13171-022-00303-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13171-022-00303-5