1 Introduction

Corona-Virus “COVID-19” was first reported in early December 2019 in Wuhan, China, and within three months spread like a pandemic around the whole globe. The World Health Organization (WHO) described COVID-19 as a pandemic on March 11, 2020. Refer to Figs. 1 and 2. Despite the drastic, large-scale containment measures implemented in most countries, these numbers rapidly increased every day—posing an unprecedented threat to the global health and economy of interconnected human societies. Countries around the world have therefore increased their efforts to decrease the COVID-19 spread rate.

Figure 1
figure 1

The situation for the daily new cases over the world by the WHO Region has been shown in Figure 1

Full size image
Figure 2
figure 2

The situation for the daily new deaths over the world by the WHO Region has been shown in Figure 2

Full size image

To model daily cases and deaths in the world, there are some mathematical/statistical models in the literature which are used to describe the dynamics of the evolution of COVID-19. The comparison of the COVID-19 epidemic dynamics among different countries is of great concern. In this regard, the researchers are making their best efforts to provide medical solutions for drugs and vaccines in reducing the risk of virus spread. The study of this aspect of science requires discrete distributions. For any researcher, the first question comes to mind- Why do we need discrete distributions? We are aware that most of the current continuous distributions do not fit adequately for modeling the cases of COVID-19 in count data analysis.

In the current situation, it is of great interest to study more about COVID-19 and compare different countries as many as possible. Therefore, in this article, an effort has been made to compare the COVID-19 pandemic outbreak in several countries around the world.

Recently, many authors introduced different discrete distributions such as natural discrete Lindley distribution has been implemented by Al-Babtain et al. (2020a, ??) to model everyday cases and deaths in the world. Almetwally et al. (2020) introduced a discrete Marshall-Olkin generalized exponential distribution to discuss the recent Egyptian cases regularly. Elbatal et al. (2022) obtained discrete odd Perks-G class of distributions. Almetwally et al. (2022) introduced discrete Marshall-Olkin inverse Toppe-Leone distribution with application to COVID-19 data. Nagy et al. (2021) discussed discrete extended odd Weibull exponential with different applications. Gillariose et al. (2021) proposed discrete generalization of the exponential model. A new discrete distribution, called discrete generalized Lindley, was analyzed by El-Morshedy et al. (2020) to examine the counts of daily coronavirus cases in Hong Kong and new daily fatalities in Iran. Maleki et al. (2020) have used an autoregressive time series model based on normal distribution of the two-piece scale mixture to estimate the recovered and reported cases of COVID-19. The study carried out by Hasab et al. (2020) where they used the susceptible infected recovered (SIR) epidemic dynamics of the COVID-19 pandemic for modelling the novel Coronavirus epidemic in Egypt. Nesteruk (2020) and Batista (2020b) have predicted regular new COVID-19 cases in China by using the mathematical model, named SIR. The logistic growth regression model used by Batista (2020a) for estimating the final size of the coronavirus outbreak and its peak time.

This research work aims to model the daily new fatalities of COVID-19 using a review of statistical models to determine the best model fitting of COVID-19 data for different countries as Angola, Ethiopia, French Guiana, El Salvador, Estonia, and Greece and aware of the risks resulting from the spread of Corona-Virus in the world. To accomplish this goal: First, we study separate models such as Poisson, geometric, negative binomial, discrete Burr, discrete Lindley, discrete alpha power inverse Lomax, discrete generalized exponential, discrete Marshall-Olkin Generalized exponential, discrete Gompertz-G-exponential, discrete Weibull, discrete inverse Weibull, exponentiated discrete Weibull, discrete Rayleigh, and new discrete Lindley. Second, in some countries such as Angola, Ethiopia, French Guiana, El Salvador, Estonia, and Greece, we define the best discrete models that match different regular Coronavirus death datasets.

The remainder of the paper is structured as follows. Discrete models are analyzed in Section 2. In Section 3, review for discrete models has been done based on survival discretization method. We discuss the parameter estimation of the discrete models in Section 4. Section 5 presents the new regular death of COVID-19 in the case of Angola, El Salvador, Estonia, and Greece to validate the use of models in suitable lifetime count results. Lastly, in Section 6, conclusions are made.

2 Review for Classical Discrete Models

In this Section, survival discretization method and some discrete distributions have been reviewed, such as Binomial, Poisson, Hypergeometric, discrete Burr, discrete Lindley, discrete alpha power inverse Lomax,discrete generalized exponential, discrete Marshall-Olkin Generalized exponential, discrete Gompertz-G-exponential, discrete Weibull, discrete inverse Weibull, exponentiated discrete Weibull, discrete Rayleigh, new discrete Lindley, negative binomial, beta-binomial, Skellam, beta negative binomial and Conway–Maxwell–Poisson distribution. We don’t use Logarithmic, Borel, discrete compound Poisson, Boltzmann, Benford’s law, Yule–Simon, Zipf’s law, and Zeta distribution because the range of x doesn’t support 0.

2.1 Binomial Distribution

The binomial distribution (bionm) can be defined, using the binomial expansion

$$ \left( p + q \right)^{n} = \sum\limits_{x = 0}^{n}{\frac{n!}{x!\left( n - x \right)!}p^{x}q^{n - x},} $$
(1)

as the distribution of a random variable X for which

$$ \Pr\left\lbrack X = x;\ p \right\rbrack = \begin{pmatrix} n \\ x \\ \end{pmatrix}p^{x}q^{n - x};x = 0,1,2,\ldots,n, $$
(2)

where p + q = 1, 0 < p < 1, and n is a positive integer. Ifn = 1, the distribution is called the distribution of Bernoulli.

2.2 Poisson Distribution

If a random variable X has a Poisson (Pois) distribution with parameter 𝜃,then its PMF is given by

$$ \Pr\left\lbrack X = x;\ \theta \right\rbrack = \frac{e^{- \theta}\theta^{x}}{x!};x = 0,\ 1,2,\ldots, $$
(3)

where 𝜃 > 0. For more information, see Johnson et al. (2005) chapter 4.

2.3 Hypergeometric Distribution

In a sample of n balls drawn without substitution from a population of (N) balls, (N𝜃) of which are white and (N − N𝜃) are black. The PMF of hypergeometric distribution is given by

$$ \Pr\left\lbrack X = x;\ \theta \right\rbrack = \frac{\begin{pmatrix} n \\ x \\ \end{pmatrix}\begin{pmatrix} N - n \\ N \theta - x \\ \end{pmatrix}}{\begin{pmatrix} N \\ N \theta\\ \end{pmatrix} }; x= 0,1,2,\dots,N. $$
(4)

For more information, see Johnson et al. (2005) chapter 6.

2.4 Waring Distribution

The distribution of Waring is a generalization of the distribution of Yule, see Johnson et al. (2005). Taking Pr[X = x] , Waring expansion proportional to the (x + 1) term in the sequence.

$$ \Pr\left\lbrack X = x;\alpha,\theta \right\rbrack = \frac{\left( \theta - \alpha \right)\left( \alpha + x - 1 \right)!\theta!}{\theta\left( \alpha - 1 \right)!\left( \theta + x \right)!};x = 0,1,2,\dots, $$
(5)

where α,𝜃 > 0. If α = 1 then, Yule distribution is the special case of Waring distribution.

2.5 Yule–Simon Distribution

The Yule–Simon distribution is a discrete probability distribution named after Udny Yule and Herbert A. Simon in probability and statistics. Originally, Simon named it the distribution of Yule by Simon (1955). The Yule-Simon (𝜃) PMF is

$$ \Pr\left\lbrack X = x;\theta \right\rbrack = \theta\frac{x!}{\left( x - \theta - 1 \right)!\left( \theta + 1 \right)!};x = 1,2,\dots, $$
(6)

where 𝜃 > 0. The CDF of Yule-Simon distribution is

$$ F\left\lbrack x;\theta \right\rbrack = 1 - x\frac{x!}{\left( x - \theta - 1 \right)!\left( \theta + 1 \right)!}. $$
(7)

The hr function of the Yule-Simon distribution is given by

$$ \text{hr}\left( x;\theta \right) = \frac{\theta}{x}. $$
(8)

2.6 Discrete Rectangular Distribution

In its most general form, the discrete rectangular distribution (sometimes called the discrete uniform distribution) is defined by

$$ \Pr\left\lbrack X = x \right\rbrack = \frac{1}{n + 1};x = 0,\ 1,2,\ldots,n. $$
(9)

2.7 Distribution of Leads

The distribution of leads in coin tossing (Johnson et al. 2005) has the PMF

$$ \Pr\left\lbrack X = x \right\rbrack = \frac{\left( 2x \right)!\left( 2n - 2x \right)!\left( 2 \right)^{- 2n}!\ }{x!x!\left( n - x \right)!\left( n - x \right)!};x = 0,\ 1,2,\ldots,n. $$
(10)

2.8 Beta-binomial Distribution

The beta-binomial (Bbinom) distribution in probability theory and statistics is a family of discrete probability distributions on finite support of non-negative integers occurring when the probability of success is either unknown or random in each of a fixed or known number of Bernoulli trials, is discussed by Griffiths (1973). The PMF of Bbinom is given by

$$ P\left( x;\alpha,\beta \right) = \begin{pmatrix} n \\ x \\ \end{pmatrix}\frac{B\left( x + \alpha,\ n - x + \beta \right)}{B\left( \alpha,\ \beta \right)}, $$
(11)

the CDF of Bbinom is given by

$$ P\left( x;\alpha,\beta \right) = \left\{ \begin{array}{cc} 0, & x < 0 \\ \begin{array}{cc} n \\ x \end{array}\frac{B\left( x + \alpha,\ n - x + \beta \right)}{B\left( \alpha,\ \beta \right)}F_{\text{GH}}\left( a,b,x \right), & 0 \leq x \leq n \\ 1, & x \geq n \end{array} \right.\ , $$
(12)

where FGH (a,b,x) is the generalized hypergeometric function.

2.9 Negative Binomial Distribution

The negative binomial(Nbionm) distribution in probability theory and statistics is a discrete probability distribution that models the number of successes before a given non-random number of failures (denoted by r) occur in a series of independent and identically distributed Bernoulli trials. The PMF of Nbinom is given by

$$ P\left( x;r,p \right) = \begin{pmatrix} x + r - 1 \\ x \\ \end{pmatrix}(1 - p)^{r}p^{x},\ x = 0,1,2,\ldots, $$
(13)

where r is a number of failures until the experiment is stopped (integer, but the definition can also be extended to real numbers) and p is success probability in each experiment. For more information, see Johnson et al. (2005) chapter 5.

2.10 Geometric Distribution

The geometric distribution in probability theory and statistics is the probability distribution of the number X − 1 of failures before the first success, supported by the set{0,1,2,... }. The PMF is given as

$$ P\left( x;p \right) = (1 - p)^{x}p,\ x = 0,1,2,\dots, $$
(14)

where0 < p < 1.

2.11 Beta Negative Binomial Distribution

A beta negative binomial (BNbinom) distribution in probability theory is the probability distribution of a discrete random variable X equal to the number of failures needed to achieve achievements in a series of independent Bernoulli trials in which the probability p of success in each trial, though constant in any given experiment, is itself a random variable following a beta distribution. Wang (2011) discussed this distribution as a compound probability distribution. The PMF of BNbinom is given by

$$ P\left( x;r,\alpha,\beta \right) = \frac{\Gamma\left( r + x \right)}{x!{\Gamma}\left( r \right)}\frac{B\left( r + \alpha,\ x + \beta \right)}{B\left( \alpha,\ \beta \right)}, $$
(15)

where x = 0, 1, 2,… and r,α,β > 0.

2.12 Logarithmic Distribution

A random variable X is said to have a logarithmic distribution with parameter 𝜃 if its PMF is in the form

$$ P\left( X = x;\theta \right) = \left\{ \begin{array}{cc} \frac{a\theta^{x}}{x} & x = 1,2,{\ldots} \\ \frac{(x - 1)\theta}{x}P\left( X = x - 1 \right) & x = 2,3,\ldots \end{array} \right.\ . $$
(16)

For more information of logarithmic distribution, see Johnson et al. (2005) chapter 7.

2.13 Skellam Distribution

Let μ1,μ2 > 0, Skellam (1946) introduced the Skellam distribution (distribution of the difference between two independent Poisson random variables) and is denoted by Skellam (μ1,μ2) with PMF is given by

$$ P\left( x;\mu_{1},\mu_{2} \right) = e^{- \left( \mu_{1} + \mu_{2} \right)}\left( \frac{\mu_{1}}{\mu_{2}} \right)^{\frac{x}{2}}I_{k}^{}\left( 2\sqrt{\mu_{1}\mu_{2}} \right), $$
(17)

wherex = …,− 2,− 1, 0, 1, 2, … Ik (2μ1 μ2) is the modified Bessel function of the first kind.

2.14 Conway–Maxwell–Poisson Distribution

Shmueli et al. (2005) discussed the Conway–Maxwell–Poisson (CMP) distribution with PMF as

$$ P\left( x;\lambda,\theta \right) = \frac{\lambda^{x}}{\left( x! \right)^{\theta}}\frac{1}{Z\left( \lambda,\theta \right)}, $$
(18)

where Z (λ,𝜃) = ∑ j= 0∞ λj (j!)𝜃 is normalization constant.

3 Review for Discrete Models Based on Survival Discretization Method

In the statistics literature, sundry methods are available to obtain a discrete distribution from a continuous one. The most commonly used technique to generate discrete distribution is called a survival discretization method, it requires the existence of cumulative distribution function (CDF), survival function should be continuous and non-negative and times are divided into unit intervals. The PMF of discrete distribution is defined in Roy (2003) as

$$ P\left( X = x \right) = P\left( x \leq X \leq x + 1 \right) = S\left( x \right) - S\left( x + 1 \right) $$
(19)

wherex = 0,1,2,…,S (x) = P (X ≥ x) = F (x; Θ), F (x; Θ) is a CDF of continuous distribution, and Θ is a vector of parameters. The random variable X is said to have the discrete distribution if its CDF is given by

$$ P\left( X < x \right) = F\left( x + 1;{\Theta} \right). $$
(20)

The hazard rate is given by hr (x) = P (X=x) S(x). The reversed failure rate of discrete distribution is given as

$$ \text{rfr}\left( x \right) = \frac{P\left( X = x \right)}{1 - S(x)}. $$
(21)

3.1 Discrete Burr Distribution

The PMF of the discrete Burr (DB) distribution has been defined by Krishna and Pundir (2009) is given by

$$ P\left( x;\theta,a \right) = \theta^{\ln\left( 1 + x^{\alpha} \right)} - \theta^{\ln\left( 1 + \left( x + 1 \right)^{\alpha} \right)}, $$
(22)

where x = 0,1,2,…, α > 0,0 < 𝜃 < 1, the CDF of the DBu distribution is

$$ F\left( x;\theta,\alpha \right) = \theta^{\ln\left( 1 + \left( x + 1 \right)^{\alpha} \right)}, $$
(23)

The hazard rate (hr) of the discrete Burr distribution is

$$ \text{hr}\left( x;\theta,\alpha \right) = 1 - \theta^{\ln\left( \frac{1 + \left( x + 1 \right)^{\alpha}}{1 + x^{\alpha}} \right)}. $$
(24)

3.2 Discrete Lindley Distribution

The PMF of the discrete Lindley (DLi) distribution has been defined by Gómez-Déniz and Calderín-Ojeda (2011) is given as follows

$$ P\left( x;\theta \right) = \frac{\theta^{x}}{1 - \ln\left( \theta \right)}\left\lbrack \theta\ln{\left( \theta \right) + \left( 1 - \theta \right)\left( 1 - \ln\left( \theta^{x + 1} \right) \right)} \right\rbrack, $$
(25)

where x = 0,1,2,…, 0 < 𝜃 < 1.

The CDF of the DLi distribution is

$$ F\left( x;\theta \right) = \frac{1 - \theta^{x + 1} + \left\lbrack \left( 2 + x \right)\theta^{x + 1} - 1 \right\rbrack\ln\left( \theta \right)}{1 - \ln\left( \theta \right)}, $$
(26)

The hazard rate of the DLi distribution is

$$ \text{hr}\left( x;\theta,\alpha \right) = \frac{\theta^{x}\left\lbrack \theta\ln{\left( \theta \right) + \left( \theta - 1 \right)\left( \ln\left( \theta^{x + 1} \right) - 1 \right)} \right\rbrack}{1 - \theta^{x + 1} + \left\lbrack \left( 2 + x \right)\theta^{x + 1} - 1 \right\rbrack\ln\left( \theta \right)}. $$
(27)

3.3 Discrete Alpha Power Inverse Lomax

The discrete alpha power inverse Lomax (DAPIL) distribution is introduced by Almetwally and Ibrahim (2020). The PMF and the CDF of the DAPIL distribution are respectively given by

$$ P\left( x;\alpha,\ \vartheta,\ \delta \right) = \frac{\alpha^{\rho^{\ln\left( 1 + \frac{\vartheta}{x + 1} \right)}} - \alpha^{\rho^{\ln\left( 1 + \frac{\vartheta}{x} \right)}}}{\alpha - 1};x = 0,1,2, $$
(28)
$$ F\left( x;\alpha,\vartheta,\ \rho \right) = \frac{\alpha^{\rho^{\ln\left( 1 + \frac{\vartheta}{x + 1} \right)}} - 1}{\alpha - 1},\ \ x \in \mathbb{N}_{0}. $$
(29)

The hr function of the DAPIL distribution is given by

$$ \text{hr}\left( x;\alpha,\vartheta,\ \rho \right) = \frac{\alpha^{\rho^{\ln\left( 1 + \frac{\vartheta}{x + 1} \right)}} - \alpha^{\rho^{\ln\left( 1 + \frac{\vartheta}{x} \right)}}}{\alpha - \alpha^{\rho^{\ln\left( 1 + \frac{\vartheta}{x + 1} \right)}}},\ \ x \in \mathbb{N}_{0}. $$
(30)

3.4 Discrete Generalized Exponential Distribution

The PMF of the discrete generalized exponential (DGE) distribution has been defined by Nekoukhou et al. (2013) is given as follows

$$ P\left( x;\theta,\ \alpha \right) = \ \left( 1 - \theta^{x + 1} \right)^{\alpha} - \left( 1 - \theta^{x} \right)^{\alpha}, $$
(31)

where x = 0,1,2,…,α > 0, 0 < 𝜃 < 1, when 𝜃 = e−λ;λ > 0, the CDF of the DGEx distribution is

$$ F\left( x;\theta \right) = \left( 1 - \theta^{x + 1} \right)^{\alpha}, $$
(32)

The hazard rate of the DGEx distribution is

$$ \text{hr}\left( x;\theta,\alpha \right) = \frac{\left( 1 - \theta^{x + 1} \right)^{\alpha} - \left( 1 - \theta^{x} \right)^{\alpha}}{1 - \left( 1 - \theta^{x + 1} \right)^{\alpha}}. $$
(33)

3.5 The DMOGEx Distribution

The discrete Marshall-Olkin Generalized exponential (DMOGEx) distribution is introduced by Almetwally et al. (2020). The PMF and the CDF of the DMOGEx distribution are respectively given by

$$ P\left( x,\alpha,\rho,\lambda \right) = \frac{\lambda\left\lbrack {1 - \left( 1 - \rho^{x} \right)}^{\alpha} \right\rbrack}{\lambda + \left( 1 - \lambda \right)\left( 1 - \rho^{x} \right)^{\alpha}} - \frac{\lambda\left\lbrack {1 - \left( 1 - \rho^{x + 1} \right)}^{\alpha} \right\rbrack}{\lambda + \left( 1 - \lambda \right)\left( 1 - \rho^{x + 1} \right)^{\alpha}}, $$
(34)

and

$$ F\left( x,\alpha,\rho,\lambda \right) = \frac{\left( 1 - \rho^{x + 1} \right)^{\alpha}}{\lambda + \left( 1 - \lambda \right)\left( 1 - \rho^{x + 1} \right)^{\alpha}},\ \ x \in \mathbb{N}_{0}, $$
(35)

where 0 < ρ < 1, λ,𝜃 > 0.

The hr function of the DMOGEx distribution is given by

$$ \text{hr}\left( x;\alpha,\rho,\lambda \right) = \frac{{1 - \left( 1 - \rho^{x} \right)}^{\alpha}}{{1 - \left( 1 - \rho^{x + 1} \right)}^{\alpha}}\frac{\lambda + \left( 1 - \lambda \right)\left( 1 - \rho^{x + 1} \right)^{\alpha}}{\lambda + \left( 1 - \lambda \right)\left( 1 - \rho^{x} \right)^{\alpha}} - 1, x \in \mathbb{N}_{0}. $$
(36)

3.6 Discrete Gompertz-G Exponential

The discrete Gompertz-G- exponential (DGzEx) distribution was introduced by Eliwa et al. (2020). The PMF and the CDF of the DGzEx distribution are respectively given by

$$ P\left( x,\alpha,\rho,\lambda \right) = \rho^{\frac{- 1}{\alpha}} \left( \rho^{\frac{1}{\alpha} e^{\lambda\alpha x}} - \rho^{\frac{1}{\alpha}e^{\lambda\alpha\left( x + 1 \right)}} \right); x \in \mathbb{N}_{0}, $$
(37)

and

$$ F\left( x,\alpha,\rho,\lambda \right) = 1 - \rho^{\frac{1}{\alpha}e^{\lambda\alpha\left( x + 1 \right)}};\ x \in \mathbb{N}_{0}. $$
(38)

The hr function of the DGzEx distribution is given by

$$ hr\left( x;\alpha,\rho,\lambda \right) = \frac{\rho^{\frac{- 1}{\alpha}}\left( \rho^{\frac{1}{\alpha}e^{\lambda\alpha x}} - \rho^{\frac{1}{\alpha}e^{\lambda\alpha\left( x + 1 \right)}} \right)}{\rho^{\frac{1}{\alpha}e^{\lambda\alpha\left( x + 1 \right)}}};\ x \in \mathbb{N}_{0}. $$
(39)

3.7 Discrete Weibull

A discrete Weibull (DW) distribution was introduced by ? Nakagawa-and-Osaki:1975 (), and is defined by the cumulative distribution function (CDF)as:

$$ F\left( x;\alpha,\ \rho \right) = 1 - \ \rho^{{(x + 1)}^{\alpha}};\ \ x \in \mathbb{N}_{0},\alpha > 0,\ 0 < \rho < 1. $$
(40)

The DW distribution has PMF:

$$ P\left( x;\alpha,\ \rho \right) = \rho^{x^{\alpha}} - \rho^{{(x + 1)}^{\alpha}}, $$
(41)

and the hazard rate of DW is

$$ h\left( x;\alpha,\ \rho \right) = \rho^{x^{\alpha} - \left( x + 1 \right)^{\alpha}} - 1. $$
(42)

3.8 Discrete Inverse Weibull

A discrete inverse Weibull (DIW) distribution was introduced by Jazi et al. (2010), and is defined by the CDF:

$$ F\left( x;\alpha,\ \rho \right) = \rho^{x^{- \alpha}};\ \alpha > 0,\ 0 < \rho < 1. $$
(43)

The DIW distribution has PMF:

$$ P\left( x;\alpha,\ \rho \right) = \rho^{x^{- \alpha}} - \rho^{\left( x - 1 \right)^{- \alpha}},\ \ x = 1,2,\ldots, $$
(44)

and the hazard rate of DIW is

$$ h\left( x;\alpha,\ \rho \right) = \frac{1 - \rho^{\left( x - 1 \right)^{- \alpha}}}{1 - \rho^{x^{- \alpha}}}. $$
(45)

3.9 Exponentiated Discrete Weibull

The exponentiated discrete Weibull (EDW) distribution was introduced by Nekoukhou and Bidram (2015), and is defined by the CDF:

$$ F\left( x;\alpha,\ \rho,\beta \right) = \left( 1 - \rho^{\left( x + 1 \right)^{\alpha}} \right)^{\beta};\ \ x \in \mathbb{N}_{0},\alpha,\beta > 0,\ 0 < \rho < 1. $$
(46)

The DIW distribution has PMF:

$$ P\left( x;\alpha,\ \rho,\beta \right) = \left( 1 - \rho^{\left( x + 1 \right)^{\alpha}} \right)^{\beta} - \left( 1 - \rho^{x^{\alpha}} \right)^{\beta}, $$
(47)

and the hazard rate of DIW is

$$ h\left( x;\alpha,\ \rho,\beta \right) = \frac{\left( 1 - \rho^{\left( x + 1 \right)^{\alpha}} \right)^{\beta} - \left( 1 - \rho^{x^{\alpha}} \right)^{\beta}}{1 - \left( 1 - \rho^{\left( x + 1 \right)^{\alpha}} \right)^{\beta}}. $$
(48)

The discrete Rayleigh (DR) distribution was introduced by Roy (2004), and can be defined when α = 2 and β = 1as follows:

$$ F\left( x;\alpha,\ \rho,\beta \right) = 1 - \rho^{\left( x + 1 \right)^{2}};\ \ x \in \mathbb{N}_{0},\ 0 < \rho < 1. $$
(49)

The DR distribution has PMF:

$$ P\left( x;\rho \right) = \rho^{x^{2}} - \rho^{\left( x + 1 \right)^{2}}, $$
(50)

and the hazard rate of DR is

$$ h\left( x;\rho \right) = \frac{\rho^{x^{2}} - \rho^{\left( x + 1 \right)^{2}}}{\rho^{\left( x + 1 \right)^{2}}}. $$
(51)

3.10 New Discrete Lindley

The new discrete Lindley (NDL) distribution was introduced by Al-Babtain et al. (2020a, ??), and is defined by the CDF:

$$ F\left( x;\alpha,\ \rho,\beta \right) = 1 - \frac{1 + \rho + \rho x}{1 + \rho}\left( 1 - \rho \right)^{x};\ \ x \in \mathbb{N}_{0},\ 0 < \rho < 1. $$
(52)

The NDL distribution has PMF:

$$ P\left( x;\rho \right) = \frac{\rho^{2}}{1 + \rho}\left( 2 + x \right)\left( 1 - \rho \right)^{x}, $$
(53)

and the hazard rate of NDL is

$$ h\left( x;\rho \right) = \frac{\rho^{2}\left( 2 + x \right)}{1 + \rho + \rho x}. $$
(54)

4 Parameter Estimation of Discrete Model

In this section, we estimate the parameters of the models using a maximum likelihood method. It is noted that the maximum likelihood method is also used to estimate unknown parameters of a statistical model because maximum likelihood estimates (MLEs) have several desirable properties; For example, they are asymptotically unbiased, symmetrical, consistent, asymptomatically normally distributed, etc. Let x1, x2,…, xn be a random sample of size n from the discrete distribution, and then the log-likelihood function is given by

$$ \mathcal{L}\left( {\Theta}|x \right) = \sum\limits_{i = 1}^{n}{\log{P\left( x_{i};{\Theta} \right)}}, $$
(55)

where Θ = (Θ1,…,Θk)T, k is a length of Θ. The MLEs can be obtained by partially first derivatives of the log-likelihood function and equal to zero

$$ \frac{\partial\mathcal{L}\left( {\Theta}|x \right)}{\partial{\Theta}_{1}} = \sum\limits_{i = 1}^{n}\frac{\frac{\partial P\left( x_{i};{\Theta} \right)}{\partial{\Theta}_{1}}}{P\left( x_{i};{\Theta} \right)},\ldots,\frac{\partial\mathcal{L}\left( {\Theta}|x \right)}{\partial{\Theta}_{k}} = \sum\limits_{i = 1}^{n}\frac{\frac{\partial P\left( x_{i};{\Theta} \right)}{\partial{\Theta}_{k}}}{P\left( x_{i};{\Theta} \right)}, $$
(56)

provide the MLEs of Θ, say Θ̂ = (Θ̂1,…,Θ̂k)T, then using a computational process such as the k variable Newton-Raphson Algorithm are given by the solutions of the equations.

For interval estimation and hypothesis tests on the model parameters, we require the information matrix. The k × k observed information matrix is

$$ I_{n}\left( \widehat{\Theta} \right) = \begin{bmatrix} \frac{\partial^{2}\mathcal{L}\left( {\Theta}|x \right)}{{\partial{\Theta}_{1}^{2}}} & {\ldots} & \frac{\partial^{2}\mathcal{L}\left( {\Theta}|x \right)}{\partial{\Theta}_{k}\partial{\Theta}_{1}} \\ {\vdots} & {\ddots} & {\vdots} \\ \frac{\partial^{2}\mathcal{L}\left( {\Theta}|x \right)}{\partial{\Theta}_{1}\partial{\Theta}_{k}} & {\ldots} & \frac{\partial^{2}\mathcal{L}\left( {\Theta}|x \right)}{{\partial{\Theta}_{k}^{2}}} \\ \end{bmatrix}. $$
(57)

One can use the normal distribution of Θ̂ to construct approximate confidence interval regions for some parameters. Indeed, an asymptotic 100(1 − ξ) confidence interval for each parameterΘj;j = 1,…,k, is given by

$$ \left( {\widehat{\Theta}}_{j} - z_{\frac{\xi}{2}}\sqrt{{\widehat{\beth}}_{jj}},\ \ {\widehat{\Theta}}_{j} + z_{\frac{\xi}{2}}\sqrt{{\widehat{\beth}}_{jj}} \right), $$
(58)

where ℶ ̂jj denotes the (i,i) diagonal element of In− 1 (Θ̂) and zξ2 is the (1 − ξ 2) thquantile of the standard normal distribution.

5 Applications of Real Data

In this section, we illustrate the empirical importance of the discrete distributions, such as DB, DLi, Binom, Pois, DR, DGE, Geometric, DW, DIW, DE, NDL, DGzEx, DMOGE, DAPLo, and EDW distributions using four applications to real data sets. The fitted models are compared using some criteria; namely, Akaike information criterion (AIC), corrected AIC (CAIC), Hannan-Quinn information criterion (HQIC), Chi-square (X2) with a degree of freedom and its p-value.

$$ \begin{array}{@{}rcl@{}} \text{AIC} = - 2\mathcal{L}\left( \widehat{\Theta}|x \right) + 2p,\\ \text{CAIC} = - 2\mathcal{L}\left( \widehat{\Theta}|x \right) + 2p +2\frac{p(p+1)}{n-p-1},\\ \text{BIC} = - 2\mathcal{L}\left( \widehat{\Theta}|x \right) + p \log (n), \end{array} $$

and

$$ \text{HQIC} = - 2\mathcal{L}\left( \widehat{\Theta}|x \right) + 2\ p \log [\log(n)]. $$

5.1 African Continent

5.1.1 Angola

This data represents the daily new deaths of 51 days from 10 October to 29 November 2020 belong to Angola country (see World Health Organization). The MLEs and the goodness of fit statistics are reported in Tables 1, 2 and 3.

Table 1 The goodness of fit and estimation models with one parameter for Dataset of Angola
Full size table
Table 2 The goodness of fit and estimation models with two parameters for Dataset of Angola
Full size table
Table 3 The goodness of fit and estimation models with three parameters for Dataset of Angola
Full size table

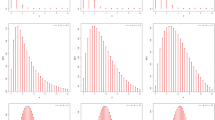
From Tables 1, 2 and 3, it is evident that all distributions are fitted and work quite well for analyzing these data except for the DB distribution. However, we always search for the best model to get the best evaluation of the data, and therefore, using AIC, BIC, CAIC, HQIC, χ2 and p-values, we can say that the DMKEx model provides the best fit among all the tested models because it has the largest p-value and the smallest values of AIC, CAIC, BIC, HQIC and χ2 statistics. Figure 1 supports the results of Tables 1, 2 and 3.

Figure 3
figure 3

The fitted PMFs for Dataset of Angola

Full size image

5.1.2 Ethiopia

This data represents the daily new deaths of 68 days from 1 April to 7 June 2020 belong to Ethiopia country (see World Health Organization). The MLEs and the goodness of fit statistics are reported in Tables 4, 5, and 6.

Table 4 The goodness of fit and estimation models with one parameter for Dataset of Ethiopia
Full size table
Table 5 The goodness of fit and estimation models with two parameters for Dataset of Ethiopia
Full size table
Table 6 The goodness of fit and estimation models with three parameters for Data set of Ethiopia
Full size table

From Tables 4, 5, and 6, it is evident that all distributions are fitted and works quite well for analyzing these data except for the DR, binomial, Poisson, Skellam, and BNbinom distributions. However, we always search for the best model to get the best evaluation by using AIC, BIC, CAIC, HQIC, χ2, and p-values. Figure 2 supports the results of Tables 4, 5 and 6.

Figure 4
figure 4

The fitted PMFs for Dataset of Ethiopia

Full size image

5.2 America Continent

5.3 El Salvador

This data represents the daily new deaths of 81 days from 1 April to 20 June 2020 belong to El Salvador country (see World Health Organization). The MLEs and the goodness of fit statistics are reported in Tables 7, 8 and 9.

Table 7 The goodness of fit and estimation models with one parameter for Dataset of El Salvador
Full size table
Table 8 The goodness of fit and estimation models with two parameters for Dataset of El Salvador
Full size table
Table 9 The goodness of fit and estimation models with three parameters for Dataset of El Salvador
Full size table

From Tables 7, 8 and 9, it is evident that all distributions are Fitted and work immensely well for analyzing these data except for the BNbionm, and DR distribution. However, we always search for the best model to get the best evaluation byusing AIC, BIC, CAIC, HQIC, χ2, and p-values. Figure 3 supports the results of Tables 7, 8 and 9.

5.3.1 French Guiana

This data represents the daily new deaths of 153 days from 1 June to 31 October 2020 belong to French Guiana country (see World Health Organization). The MLEs and the goodness of fit statistics are reported in Tables 10, 11 and 12.

Table 10 The goodness of fit and estimation models with one parameter for Dataset of French Guiana
Full size table
Table 11 The goodness of fit and estimation models with two parameters for Dataset of French Guiana
Full size table
Table 12 The goodness of fit and estimation models with three parameters for Dataset of French Guiana
Full size table

From Tables 10, 11 and 12, it is evident that all distributions are fitted and work immensely well for analyzing these data except for the DR and skellam distributions. However, we always search for the best model to get the best evaluation of the data, and therefore, using AIC, BIC, CAIC, HQIC, X2, and p-values, we can say that the DL in Table 7, DGE in Table 8, and DMOGE in Table 9 model provides the best fit among all the tested models because it has the largest p-value and the smallest values of AIC, CAIC, BIC, HQIC and χ2 statistics. Figure 4 supports the results of Tables 10, 11 and 12.

5.4 Europe Continent

5.4.1 Estonia

This data represents the daily new deaths of 81 days from 1 April to 20 May 2020 belong to Estonia country (see World Health Organization). The MLEs and the goodness of fit statistics are reported in Tables 13, 14 and 15.

Table 13 The goodness of fit and estimation models with one parameter for Dataset of Estonia
Full size table
Table 14 The goodness of fit and estimation models with two parameters for Dataset of Estonia
Full size table
Table 15 The goodness of fit and estimation models with three parameters for Dataset of Estonia
Full size table

From Tables 13, 14, and 15, it is evident that all distributions are Fitted and work quite well for analyzing these data except for the Binom, Pois, and DR distributions. However, we always search for the best model to get the best evaluation of the data, and therefore, using AIC, BIC, CAIC, HQIC, X2, and p-values, we can say that the DL model provides the best fit among all the tested models because it has the smallest values of AIC, CAIC, BIC, HQIC, and χ2 statistics, as well as having the highest p-value. Figure 5 supports the results of Tables 13, 14 and 15.

Figure 5
figure 5

The fitted PMFs for Dataset of El Salvador

Full size image

5.4.2 Greece

This data represents the daily new deaths of 111 days from 12 March to 30 June 2020 belong to Greece country (see World Health Organization). The MLEs and the goodness of fit statistics are reported in Tables 16, 17 and 18.

Table 16 The goodness of fit and estimation models with one parameter for Dataset of Greece
Full size table
Table 17 The goodness of fit and estimation models with two parameters for Dataset of Greece
Full size table
Table 18 The goodness of fit and estimation models with three parameters for Dataset of Greece
Full size table

From Tables 16, 17 and 18, it is evident that all distributions are Fitted and work quite well for analyzing these data except for the DB, Binom, Pois, DIW, and DR distribution. However, we always search for the best model to get the best evaluation of the data, and therefore, concerning the AIC, BIC, CAIC, HQIC, χ2and p-values, we can say that the DE model provides the best fit among all the tested models because it has the smallest values of AIC, CAIC, BIC, HQIC and χ2statistics, as well as having the highest p-value. Figures 6, 7 and 8 support the results of Tables 16, 17 and 18.

Figure 6
figure 6

The fitted PMFs for Dataset of Guiana

Full size image
Figure 7
figure 7

The fitted PMFs for Dataset of Estonia

Full size image
Figure 8
figure 8

The fitted PMFs for Dataset of Greece

Full size image

6 Concluding Remarks

In this article, we use 8 discrete distributions with one parameter, 7 discrete distributions with two parameters, and 4 discrete distributions with three parameters to fit and determine the best model of daily Coronavirus deaths in some countries, such as Angola,Ethiopia, French Guiana, El Salvador, Estonia, and Greece. In the case of discrete distributions with one parameter, we discussed DL, binomial, Poisson, DR, Geometric, DE, Nbinom, and NDL distributions. In the case of discrete distributions with two parameters, we discussed DB, DGE, DW, DIW, Bbinom, BNbinom, and skellam distributions. In the case of discrete distributions with three parameters, we discussed DGzEx, DMOGE, DAPL, and EDW distributions. A review of some important discrete distributions has been provided as DB, DL, DMOGE, DGE, DAPL, DR, DE, Geometric, Binomial, NDL, DGzEx, and EDW distribution. The maximum likelihood estimation method is discussed to estimate the parameters of the discrete distributions. We prove empirically that the discrete models fit different datasets of daily Coronavirus deaths in some countries as Angola, Ethiopia, French Guiana, El Salvador, Estonia, and Greece. DW and DB reveal its superiority over other competitive models for the analysis of daily deaths of the COVID-19 in the case of Angola, Ethiopia, French Guiana, El Salvador, Estonia, and Greece.