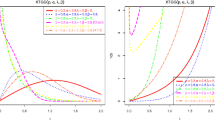
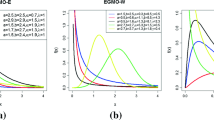
Abstract
Asadi and Zohrevand (2007). On the dynamic cumulative residual entropy. J. Statist. Plann. Inference, 137, 1931–1941] define the decreasing dynamic cumulative residual entropy (DDCRE) class of life distributions, some properties of the DDCRE class are studied. Navarro et al. (2010). Some new results on the cumulative residual entropy. J. Statist. Plann. Inference, 140, 310–322] further investigate this class, they get some results concerning the relations between the DDCRE class and other classes of distributions. In the present paper some characterization properties of the DDCRE class are investigated, closure and reversed closure properties of this class are obtained.
Similar content being viewed by others
References
Asadi M. and Ebrahimi N. (2000). Residual entropy and its characterizations in terms of hazard function and mean residual life function. Statist. Probab. Lett., 49, 263–269.
Asadi M. and Zohrevand Y. (2007). On the dynamic cumulative residual entropy. J. Statist. Plann. Inference, 137, 1931–1941.
Barlow R.E. and Proschan F. 1981 .Statistical Theory of Reliability and Life Testing, To Begin with, Silver Spring, Maryland.
Belzunce F., Navarro J., Ruiz J.M., and del Aguila Y. (2004). Some results on residual entropy function. Metrika, 59, 47–161.
Di Crescenzo A. and Longobardi M. (2002). Entropy-based measure of uncertainty in past lifetime distributions. J. Appl. Probab., 39, 434–440.
Di Crescenzo A. and Longobardi M. (2006). On weighted and residual and past entropies. Scientiae Math. Japan, 64, 255–266.
Ebrahimi N. (1996). How to measure uncertainty in the residual lifetime distribution. Sankhyā A, 58, 48–56.
Ebrahimi N. and Kirmani S.N.U.A. (1996). Some results on odering of survival functions through uncertainty. Statist. Probab. Lett., 29, 167–176.
Ebrahimi N. and Pellerey F. (1995). New partial ordering of survival functions based on the notion of uncertainty. J. Appl. Probab., 32, 202–211.
Khorashadizadeh M., Rezaei Roknabadi A.H., and Mohtashami Borzadaran G.R. (2013). Doubly truncated (interval) cumulative residual and past entropy. Statist. Probab. Lett., 83, 1464–1471.
Kumar V. and Taneja H.C. (2011). Some characterization results on generalized cumulative residual entropy measure. Statist. Probab. Lett., 81, 1072–1077.
Li X. and Zhang S. (2011). Some new results on Rényi entropy of residual life and inactivity time. Prob. Eng. Inf. Sci., 25, 237–250.
Li X. and Zuo M.J. (2004). Preservation of stochastic orders for random minima and maxima, with applications. Naval Res. Logist., 51, 332–344.
Navarro J., del Aguila Y., and Asadi M. (2010). Some new results on the cumulative residual entropy. J. Statist. Plann. Inference, 140, 310–322.
Rao M., Chen Y., Vernuri B.C., and Wang F. (2004). Cumulative residual entropy: a new measure of information. IEEE Trans. Inform. Theory, 50, 1220–1228.
Shaked M. and Shanthikumar J.G. (1994). Stochastic Orders and Their Applications. Academic Press, San Diego.
Shaked M. and Shanthikumar J.G. (2007). Stochastic Orders. Springer, New York.
Shannon C.E. (1948). A mathematical theory of comunication. Bell Syst. Tech. J., 27, 379–423.
Sunoj S.M. and Sankaran P.G. (2012). Quantile based entropy function. Statist. Probab. Lett., 82, 1049–1053.
Sunoj S.M., Sankaran P.G., and Nanda A.K. (2013). Quantile based entropy function in past lifetime. Statist. Probab. Lett., 83, 366–372.
Taneja I.J. 1990 . On Generalized Entropy with Applications. In Lectures in Applied Mathematics and Informatics, (L.M. Ricciardi, ed.). Manchester University Press, pp. 107–169.
Wiener N. (1961). Cybernetics, 2nd edn. MIT Press, Wiley, New York.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kang, Dt. Some Results on DDCRE Class of Life Distributions. Sankhya A 77, 351–363 (2015). https://doi.org/10.1007/s13171-014-0065-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13171-014-0065-0