Skip to main content
SpringerLink
Log in

Traveling wave solutions in a diffusive predator–prey system with Holling type-III functional response

  • Original Paper
  • Published:
Japan Journal of Industrial and Applied Mathematics Aims and scope Submit manuscript

Abstract

This work concerns with the existence of traveling wave solutions for the following diffusive predator–prey type system with Holling type-III functional response:

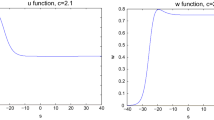
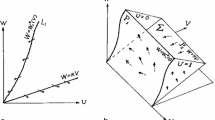
$$\begin{aligned} \begin{array}{l} u_{t}(x,t)=d_{1} u_{xx}(x,t)+Au(x,t)\big (1-\frac{u(x,t)}{K}\big )-\varphi (u(x,t))w(x,t),\\ w_{t}(x,t)=d_{2} w_{xx}(x,t)+w(x,t)\big (\mu \varphi (u(x,t))-C\big ), \end{array} \end{aligned}$$

where all parameters are positive which will be mentioned later. The traveling wave solutions are established in \(\varvec{R}^{4}\), which is a heteroclinic orbit connecting the boundary equilibrium and the positive equilibrium. Applying the methods of Wazewski Theorem and LaSalle’s Invariance Principle, and constructing a Liapunov function, we obtain the existence of traveling wave solutions. We also discuss some possible biological implications of the existence of these waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Berryman, A.A.: The origins and evolution of predator–prey theory. Ecology 73, 1530–1535 (1992)

    Article  Google Scholar 

  2. Fan, Y., Li, W., Wang, L.: Global asymptotic stability of a ratio-dependent predator–prey system with diffusion. J. Comput. Appl. Math. 188, 205–227 (2005)

    Article  MathSciNet  Google Scholar 

  3. Gourley, S.A., Britton, N.F.: A predator–prey reaction–diffusion system nonlocal effects. J. Math. Biol. 34, 297–333 (1996)

    Article  MathSciNet  Google Scholar 

  4. Wang, L., Li, W.: Periodic solutions and permance for a delayed nonautonomous ratio-dependent predator-prey model with Holling type functional response. J. Comput. Appl. Math. 162, 341–357 (2004)

    Article  MathSciNet  Google Scholar 

  5. Freedman, H.I.: Deterministic Mathematical Models in Population Ecology. Marcel Dekker, New York (1980)

    MATH  Google Scholar 

  6. Gardner, R.: Existence of traveling wave solutions of predator–prey systems via the connection index. SIAM J. Appl. Math. 44, 56–79 (1984)

    Article  MathSciNet  Google Scholar 

  7. May, R.: Stability and Complexity in Model Ecosystems. Princeton University Press, Princeton (1974)

    Google Scholar 

  8. Murray, J.D.: Mathematical Biology. Spring, Berlin (1998)

    MATH  Google Scholar 

  9. Mischaikow, K., Reineck, J.F.: Traveling waves in predator–prey systems. SIMA J. Math. Anal. 24, 987–1008 (1993)

    Article  Google Scholar 

  10. Dunbar, S.: Traveling wave solutions of diffusive predator–prey equations: periodic orbits and point-to-periodic hertocline orbits. SIAM J. Appl. Math. 46, 1057–1078 (1986)

    Article  MathSciNet  Google Scholar 

  11. Owen, M.R., Lewis, M.A.: How predation can slow, stop or reverse a prey invasion. Bull. Math. Biol. 63, 655–684 (2001)

    Article  MathSciNet  Google Scholar 

  12. Huang, J., Lu, G., Ruan, S.: Existence of traveling wave solutions in a diffusive predator–prey model. J. Math. Biol. 46, 132–152 (2003)

    Article  MathSciNet  Google Scholar 

  13. Dunbar, S.: Traveling wave solutions of diffusive predator–prey equations. J. Math. Biol. 17, 11–32 (1983)

    Article  MathSciNet  Google Scholar 

  14. Dunbar, S.: Traveling wave solutions of diffusive predator-prey equations: a heteroclinic connection in \(R^{4}\). Trans. Am. Math. Soc. 286, 557–594 (1984)

    MATH  Google Scholar 

  15. Li, W., Wu, S.: Traveling waves in a diffusive predator–prey model with holling type-III functional response. Chaos Solitons Fractals 37, 476–486 (2008)

    Article  MathSciNet  Google Scholar 

  16. Hartman, P.: Ordinary Differential Equations. Wiley, New York (1973)

    MATH  Google Scholar 

  17. LaSalle, J.P.: Stability theory for ordinary, differential equations. J. Differ. Equ. 4, 57–65 (1968)

    Article  MathSciNet  Google Scholar 

  18. Chow, P.L., Tam, W.C.: Periodic and traveling wave solutions to Volterra–Lotka equations with diffusion. Bull. Math. Biol. 12, 643–658 (1976)

    Article  MathSciNet  Google Scholar 

  19. Gantmacher, F.R.: The Theory of Matrices. Chelsea, New York (1964)

    Google Scholar 

  20. Xu, R., Chaplain, M., Davidson, F.A.: Travelling wave and convergence in stage-structured reaction–diffusion competitive models with nonlocal delays. Chaos Solitons Fractals 30, 974–992 (2006)

    Article  MathSciNet  Google Scholar 

  21. Zhang, S., Tan, D., Chen, L.: Chaotic behavior of a chemostat model with Beddington-DeAngelis functional response and periodically impulsive invasion. Chaos Solitons Fractals 29, 474–482 (2006)

    Article  MathSciNet  Google Scholar 

  22. Hung, L.: Exact traveling wave solutions for diffusive Lotka–Volterra systems of two competing species. Jpn. J. Ind. Appl. Math. 29, 237–251 (2012)

    Article  MathSciNet  Google Scholar 

  23. Mukherjee, D., Maji, C.: Bifurcation analysis of a Holling type II predator–prey model with refuge. Chin. J. Phys. 65, 153–162 (2020)

    Article  MathSciNet  Google Scholar 

  24. Rihan, F.A., Rajivganthi, C.: Dynamics of fractional-order delay differential model of prey–predator system with Holling-type III and infection among predators. Chaos Solitons Fractals 141, 110365 (2020)

  25. Chen, Y., Guo, J.: Traveling wave solutions for a three-species predator–prey model with two aborigine preys. Jpn. J. Ind. Appl. Math. 22, 1–17 (2020)

    MathSciNet  Google Scholar 

Download references

Funding

Science and Technology Project Founded by the Education Department of Jiangxi Province(No. GJJ191645).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Sichuan Normal University, Chengdu, 610068, China

    Deniu Yang

  2. College of Mathematics and Information Science, Nanchang Hangkong University, Nanchang, 330063, China

    Minghuan Liu

Authors
  1. Deniu Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Minghuan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Minghuan Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, D., Liu, M. Traveling wave solutions in a diffusive predator–prey system with Holling type-III functional response. Japan J. Indust. Appl. Math. 39, 97–118 (2022). https://doi.org/10.1007/s13160-021-00478-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13160-021-00478-8

Keywords

Mathematics Subject Classification

Search

Navigation