New approach to evaluate the asymptotic distribution of particle systems expressed by probabilistic cellular automata

Abstract

We propose some conjectures on the asymptotic distribution of the probabilistic Burgers cellular automaton (PBCA), which is defined by a simple rule of particle motion with a probabilistic parameter. Asymptotic distribution of configurations converges to a unique steady state for PBCA. We propose a new and widely-applicable approach to analyze probabilistic particle systems and apply it concretely to PBCA and its extensions. We introduce a conjecture on the distribution and derive the asymptotic probability expressed by the GKZ hypergeometric function. If the space size goes into infinity, we can evaluate the relationship between the density and flux of particles for infinite space. Moreover, we propose two extended systems of PBCA and analyze their asymptotic behavior.

1 Introduction

Cellular automata (CA) are dynamical systems with discrete time, discrete space, and a finite set of state values. Their dynamics are generally determined by a simple rule that depends on the values of the neighboring space sites. This simple abstraction has interesting mathematical properties and has been studied in theoretical and applied research. For example, systems called “elementary cellular automata” (ECA) were classified according to the behavior of their solutions and have been extensively studied by many researchers [1,2,3,4].

There exist 256 independent rules for ECA. ECA with one of the rules, Rule 184, is known as a non-trivial particle system. It is also called Burgers cellular automaton (BCA) since it can be derived from Burgers equation by using the ultradiscretization method, which was discovered in the field of integrable systems [4]. There exists a threshold of the density of particles, and the asymptotic behavior of solutions drastically changes between the regions of lower and higher density. Thus, a phase transition occurs for BCA at the threshold. If we consider that the dynamics of BCA represents a transportation system with cars, this phase transition can be interpreted as a primitive model of occurrence of traffic jams.

We can introduce probabilistic parameters into the deterministic CA; this topic has also been extensively researched in theory and practice. For example, the asymmetric simple exclusive process (ASEP) is a well-known standard statistical model for a simple stochastic particle system. It is a random walk model of multiple particles, where each particle moves to the neighboring sites with an excluded volume effect. Various exact evaluations of statistical results have been completed for ASEP [5,6,7,8,9]. Sasamoto et al. revealed exact relations between ASEP and the orthogonal polynomials [10].

Moreover, several probabilistic CA represent realistic dynamical systems. For example, Nagel and Schreckenberg proposed a quite efficient dynamical model to investigate the physics of traffic jams, known as Nagel–Schreckenberg (NS) model [11]. They applied their model to real freeway traffic and obtained good accordance between the observed data and their theoretical estimation [12].

In previous publications, the author and his co-workers analyzed the asymptotic behavior of probabilistic CA with 4 neighbors or with a higher order of conserved quantities [13, 14]. There exist some bilinear equations for probabilities of local patterns in the asymptotic solutions of the systems. Using these equations, they derived a theoretical expression of the relationship between density and flux for the asymptotic behavior, which is called a fundamental diagram (FD).

In this paper, we focus on a probabilistic extension of BCA (PBCA). It is partially equivalent to the “totally” asymmetric simple exclusion process (TASEP) obtained by restricting the motion of particles of ASEP to the only one direction [6, 7, 15]. However, PBCA and TASEP update particle positions differently. Although one of the particles to be updated is chosen at every time step in TASEP, the “parallel-update” is used for PBCA: motions of all particles from the current time step to the next time step are determined simultaneously.

We report a new analysis to understand the asymptotic behavior of parallel-updated PBCA with the periodic boundary condition. We can consider PBCA as a one-dimensional random process and derive a transition matrix for the process. Assuming the random process is ergodic, we propose a conjecture on the asymptotic distribution of the system. Using the conjecture, we can derive the asymptotic probability of each configuration of particles in space sites and can derive FD from their expected values. Moreover, we give the expression of FD of PBCA by a hypergeometric function proposed by Gelfand, Kapranov, and Zelevinsky (GKZ). It is called the GKZ hypergeometric function and is obtained by extending the hypergeometric function of a single variable to multiple variables [16]. They obey the specific forms of differential equations, and their contiguity relation can be obtained in the form of matrix [17,18,19]. The FD of PBCA with an infinite number of space sites is calculated by using the limit of the contiguity relations. This limiting case coincides with that of previous research based on a specific ansatz [11]. Furthermore, we propose two types of extensions of PBCA and derive the asymptotic probability of configurations and FD using a similar conjecture for PBCA.

The contents of this paper are as follows. In Sect. 2, we introduce definition and properties of PBCA, and we present a new type of analysis of PBCA. In Sect. 3, we propose two types of extensions of PBCA and present the results based on the similar conjecture of PBCA. One of the extensions is a system of which motion rule of particle depends on four neighbors. The other is an extension of PBCA to a coupled system. In Sect. 4, we give the conclusion. In Appendix A, we show calculation of PBCA using the GKZ hypergeometric function when the space size goes into infinity.

2 Probabilistic Burgers cellular automaton

2.1 Definition of particle system

A probabilistic Burgers cellular automaton (PBCA) is defined by the following max-plus equation:

$$\begin{aligned} u_j^{n+1}=u_j^n +q_{j-1}^n-q_{j}^n,\qquad u_j^n \in \{0,1\}, \end{aligned}$$

(1)

where

$$\begin{aligned} q_j^{n}=\min (a_j^n,u_j^n,1-u_{j+1}^n), \qquad a_j^n= {\left\{ \begin{array}{ll} 1 &{} (\text {prob. } \alpha ) \\ 0 &{} (1-\alpha ) \end{array}\right. }. \end{aligned}$$

Subscript j is an integer site number, and superscript n is integer time. Real constant $\alpha$ satisfies $0\le \alpha \le 1$. The value of probabilistic parameter $a_j^n$ is determined independently for every (j, n). We assume a periodic boundary condition for the space sites with a period L, that is, $u_{j+L}^n=u_j^n$. From the above evolution equation, it is easily shown that

$$\begin{aligned} \sum _{j=1}^{L}u_j^{n+1}=\sum _{j=1}^{L}u_j^{n}. \end{aligned}$$

(2)

Here, $u_j^n$ is the number of particles at site j and time n. Thus, the sum of all state values over L is conserved for n and is determined by the initial data. The rule of particle motion for PBCA can be expressed as follows:

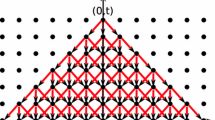
The particle at jth site moves to the right with probability $\alpha$ only if no particle exists at ($j+1$)th site. Figure 1 shows an example of time evolution in a PBCA.

Fig. 1

Example of time evolution in a PBCA for $\alpha =0.5$. Black squares $\blacksquare$ mean $u=1$ and white squares $\square$$u=0$

2.2 Asymptotic distribution of PBCA

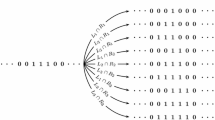
Supposing that a set of values over all L sites corresponds to a configuration of a random process, PBCA is a one-dimensional random process on ${}_L {\text {C}}_m$ configurations if $m=\sum _{j=1}^Lu_j^n$, that is, if m particles move through the sites. Figure 2a shows a histogram of all configurations from $n=0$ to $n=1000$ obtained by a numerical computation. Figure 2b–d show those from n = 0 to n = 10,000, 100,000, and 1,000,000, respectively. These figures suggest that the distribution of configurations converges after enough time steps. Moreover, the heights of bins can be divided into classes after enough time steps.

Fig. 2

Histograms of configurations for $L=8$, $m=4$ and $\alpha =0.5$

We made various numerical calculations on the histogram and an approximately unique steady state is always obtained. Therefore, we can assume that PBCA is ergodic. To illustrate our assumption and to explain the relation among heights of classes, we show the exact results for some small L and m.

For $L=4$ and $m=2$, a set of all configurations (which is denoted by $\varOmega$) is

$$\begin{aligned} \varOmega =\{0011,\ 0110,\ 1100,\ 1001,\ 0101,\ 1010\}, \end{aligned}$$

and transition probabilities are obtained as

$$\begin{aligned} \begin{aligned} 1010 \quad&\rightarrow \quad 0101 \quad \hbox {with probability} \quad \alpha ^2 \\ 1010 \quad&\rightarrow \quad 1001 \quad \hbox {with probability} \quad \alpha (1-\alpha ) \\ 1010 \quad&\rightarrow \quad 0110 \quad \hbox {with probability} \quad \alpha (1-\alpha ) \\ 1010 \quad&\rightarrow \quad 1010 \quad \hbox {with probability} \quad (1-\alpha )^2 \\&\,\, \vdots \end{aligned} \end{aligned}$$

Then, a transition matrix $A=(a_{ij})$ is

$$\begin{aligned} \begin{array}{c} 0011\\ 0110\\ 1100\\ 1001\\ 0101\\ 1010 \end{array} \left( \begin{array}{cccccc} 1-\alpha &{} 0 &{} 0 &{} 0 &{} 0 &{} \alpha \\ 0 &{} 1-\alpha &{} 0 &{} 0 &{} \alpha &{} 0 \\ 0 &{} 0 &{} 1-\alpha &{} 0 &{} 0 &{} \alpha \\ 0 &{} 0 &{} 0 &{} 1-\alpha &{} \alpha &{} 0 \\ \alpha (1-\alpha ) &{} 0 &{} \alpha (1-\alpha ) &{} 0 &{} (1-\alpha )^2 &{} \alpha ^2 \\ 0 &{} \alpha (1-\alpha ) &{} 0 &{} \alpha (1-\alpha ) &{} \alpha ^2 &{} (1-\alpha )^2 \\ \end{array} \right) , \end{aligned}$$

where $a_{ij}$ is a transition probability from the ith configuration to the jth configuration. The characteristic equation for the matrix has a simple root 1, and the absolute value of other roots is always less than 1. Subsequently, time evolution of the random process determined by this matrix has a unique steady state, and an eigenvector of the matrix for eigenvalue 1 becomes the asymptotic distribution of configurations. The corresponding eigenvector is

$$\begin{aligned} (1-\alpha ,\ 1-\alpha ,\ 1-\alpha ,\ 1-\alpha ,\ 1,\ 1) \end{aligned}$$

and components of this eigenvector give the ratios of heights of the histogram.

Let us consider another example: $L=6$ and $m=3$. All elements of a set of configurations $\varOmega$ are

$$\begin{aligned} \begin{array}{l} 000111,\ 001110,\ 011100,\ 111000, \ 110001,\ 100011,\ 001011,\ 010110,\\ 101100,\ 011001,\ 110010,\ 100101,\ 010011,\ 100110,\ 001101,\ 011010,\\ 110100,\ 101001,\ 010101,\ 101010. \end{array} \end{aligned}$$

The transition matrix is

$$\begin{aligned} \begin{array}{c} 000111\\ 001110\\ 011100\\ \vdots \\ 110100 \\ 101001 \\ 010101 \\ 101010 \end{array} \left( \begin{array}{cccccccc} 1 - \alpha &{} 0 &{} 0 &{} \ldots &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 - \alpha &{} 0 &{} \ldots &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 - \alpha &{} \ldots &{} 0 &{} 0 &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \ldots &{} (1-\alpha )^2 &{} 0 &{} 0 &{} \alpha ^2 \\ 0 &{} 0 &{} 0 &{} \ldots &{} 0 &{} (1-\alpha )^2 &{} \alpha ^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} \ldots &{} \alpha (1-\alpha )^2 &{} 0 &{} (1-\alpha )^3 &{} \alpha ^3 \\ 0 &{} 0 &{} 0 &{} \ldots &{} 0 &{} \alpha (1-\alpha )^2 &{} \alpha ^3 &{} (1-\alpha )^3 \\ \end{array} \right) , \end{aligned}$$

and its eigenvector for eigenvalue 1 as a simple root of the characteristic equation is

$$\begin{aligned} \left( \overbrace{(1-\alpha )^2,\ldots (1-\alpha )^2}^{\text{6\, components}},\overbrace{1-\alpha ,\ldots 1-\alpha }^{\text{12\, components}}, 1, 1\right) . \end{aligned}$$

We propose the following conjecture from the exact results obtained for small L and the numerical results for large L and m. To give the conjecture, let us introduce some notations. Define $\varOmega$ as a set of all configurations for L and m, $x=x_1 x_2\cdots x_L$ ($x_i \in \{ 0,1 \}$) as any configuration of $\varOmega$, $\#s_1 s_2\cdots s_k(x)$ ($1 \le k \le L$) as the number of patterns $s_1 s_2\cdots s_k$ included in x considering the periodic boundary condition, and p(x) as the probability of x in the steady state.

• Conjecture: For any $x\in \varOmega$, we have

  $$\begin{aligned} p(x)=\frac{C}{(1-\alpha )^{\#10(x)}}, \end{aligned}$$

  where C is a normalization constant satisfying $\sum _{x\in \varOmega } p(x)=1$.

Considering the case of $L=4$ and $m=2$ as an example, we have

$$\begin{aligned} \#10=1:p(0011)& = p(0110)=p(1100)=p(1001)=\frac{C}{1-\alpha }, \\ \#10=2:p(0101)& = p(1010)=\frac{C}{(1-\alpha )^2}. \end{aligned}$$

Since $p(0011)+p(0110)+\cdots +p(1010)=1$, we have $C=(1-\alpha )^2/(4(1-\alpha )+2)$ and

$$\begin{aligned} p(0011)=\frac{1-\alpha }{4(1-\alpha )+2}, \qquad p(0101)=\frac{1}{4(1-\alpha )+2}. \end{aligned}$$

Considering another case of $L=11$, and $m=6$, we have

$$\begin{aligned}&\#10=1:p(11111100000)=p(01111110000)=\cdots =\frac{C}{1-\alpha }, \\&\#10=2:p(11110110000)=p(10011100011)=\cdots =\frac{C}{(1-\alpha )^2}, \\&\#10=3:p(11101101000)=p(11011001100)=\cdots =\frac{C}{(1-\alpha )^3}, \\&\qquad \cdots . \end{aligned}$$

By the above-mentioned conjecture, we can categorize the probability by $\#10$. Then, the probability of a configuration x with $\#10(x)$ obtained in the limit $n\rightarrow \infty$ for the space size L and the number of particles m is

$$\begin{aligned} p(x)=\frac{\left( \frac{1}{1-\alpha }\right) ^{\#10(x)}}{\sum _{k=1}^m N_{L,m}(k)\left( \frac{1}{1-\alpha }\right) ^{k}} \qquad (0<\alpha <1), \end{aligned}$$

where $N_{L,m}(k)$ is the number of configurations with $\#10=k$ defined by

$$\begin{aligned} N_{L,m}(k)=\frac{L(m-1)!(L-m-1)! }{(m-k)!(k-1)!k! (L-m-k)!}. \end{aligned}$$

2.3 Fundamental diagram of PBCA

A fundamental diagram (FD) of a general particle system is a diagram that shows the relation between the density and flux of the particles averaged over all sites in the limit $n\rightarrow \infty$. Since PBCA is also a particle system, we can derive its FD. Density $\rho$ is defined by m/L, where L and m are the number of sites and particles, respectively. Let $Q_{L,\alpha }(m)$ be the expected values of flux of the steady state, where $\alpha$ is the hopping probability of a particle. Then, $Q_{L,\alpha }(m)$ of PBCA is an expected value of $\alpha \#10/L$, since only particles next to an empty site can move with probability $\alpha$. Thus, we have

$$\begin{aligned} Q_{L,\alpha }(m)=\frac{\alpha }{L}\frac{\sum _{k=1}^{m} k\,N_{L,m}(k)\left( \frac{1}{1-\alpha }\right) ^k}{\sum _{k=1}^{m} N_{L,m}(k)\left( \frac{1}{1-\alpha }\right) ^k} \qquad (0<m<L). \end{aligned}$$

(3)

Figure 3 shows FD obtained by (3) and that by the numerical calculation. The former is shown by small black circles ($\bullet$) and the latter by white circles ($\bigcirc$). Their good coincidence can be observed from this figure.

Fig. 3

Example of FD. Small black circles ($\bullet$) are obtained by (3) for $L=100$ and $\alpha =0.8$, and white circles ($\bigcirc$) are obtained numerically for the same L and $\alpha$ averaged from $n=0$ to 50,000

Utilizing GKZ hypergeometric function, we can evaluate $Q_{L,\alpha }(m)$ in the limit of $L\rightarrow \infty$ preserving $m=\rho L$ as

$$\begin{aligned} Q=\lim _{\begin{array}{c} L\rightarrow \infty \\ m=\rho L \end{array}} Q_{L,\alpha }(m)=\frac{1-\sqrt{1-4\alpha \rho (1-\rho )}}{2}, \end{aligned}$$

(4)

which coincides with the result of previous research [11]. We show the proof of this derivation in the Appendix A [17,18,19].

3 Extended systems and their properties

In this section, we introduce two systems that are extensions of PBCA. We evaluate their asymptotic probability of configurations and derive their FD, as we have shown in the previous section. Note that we also assume the ergodicity for both systems.

3.1 Extension to 4 neighbors

Let us consider the probabilistic CA expressed by a max-plus equation,

$$\begin{aligned} u_j^{n+1}=u_j^n +q_{j-1}^n-q_{j}^n, \end{aligned}$$

where

$$\begin{aligned} q_j^n=\max (\min (u_{j}^n,1-u_{j+1}^n,u_{j+2}^n,b_j^n),\min (u_{j}^n,1-u_{j+1}^n,1-u_{j+2}^n,a_j^n)). \end{aligned}$$

(5)

The probabilistic parameters $a_j^n$ and $b_j^n$ are defined by

$$\begin{aligned} a_j^n= {\left\{ \begin{array}{ll} 1 &{} (\text {prob. }\alpha ) \\ 0 &{} (1-\alpha ), \end{array}\right. } \qquad b_j^n= {\left\{ \begin{array}{ll} 1 &{} (\text {prob. }\beta ) \\ 0 &{} (1-\beta ). \end{array}\right. } \end{aligned}$$

Since this equation is also in the conservation form, the number of particles ($=\sum _{j} u_j^n$) is preserved during the time evolution. From the max-plus expression of flow $q_j^n$, we can easily show the motion rule of particles denoted by 1 as follows.

Note that any particle in the configuration other than 100 and 101 can not move. We call this system EPBCA1. In the case of $\alpha =\beta$, any particle in the pattern “10” moves with probability $\alpha$. Thus, PBCA is included in EPBCA1 as a special case. Figure 4 shows an example of time evolution of the system.

Fig. 4

Example of time evolution in the EPBCA1 for $\alpha =0.8$ and $\beta =0.1$. Black squares $\blacksquare$ mean $u=1$ and white squares $\square$ mean $u=0$

We can obtain an exact form of the transition matrix and of eigenvector for eigenvalue 1 for small values of the space size L and the number of particles m. Then, we give a conjecture for asymptotic distribution of EPBCA1 from those results. Let us introduce two examples that support our conjecture.

Suppose a set of configurations $\varOmega$ for $L=8$ and $m=4$. Size of $\varOmega$ is 70. To make the expression of the transition matrix compact, we define classes of configurations up to cyclic rotation and divide $\varOmega$ into the equivalence classes. The number of the equivalence classes is 10, and their representative elements are as follows.

$$\begin{aligned}&00001111,\ 00010111,\ 00011011,\ 00011101,\ 00100111, \\&00101011,\ 00101101,\ 00110011,\ 00110101,\ 01010101. \end{aligned}$$

Thus, a transition matrix derived by transition probabilities from each representative element to the others is

$$\begin{aligned} \begin{array}{c} 00001111\\ 00010111\\ 00011011\\ \vdots \\ 01010101 \end{array} \left( \begin{array}{ccccc} 1 - \alpha &{} 0 &{} 0 &{} \ldots &{} 0 \\ (1-\alpha )\beta &{} (1 - \alpha )(1-\beta ) &{} 0 &{} \ldots &{} 0 \\ 0 &{} (1-\alpha )\beta &{} (1 - \alpha )(1-\beta ) &{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \ldots &{} (1-\beta )^4+\beta ^4 \\ \end{array} \right) , \end{aligned}$$

and an eigenvector for eigenvalue 1 is

$$\begin{aligned}&\left( \frac{4(1-\alpha )^2\beta ^3(1-\beta )}{\alpha ^3},\ \frac{4(1-\alpha )\beta ^2(1-\beta )}{\alpha ^2},\ \frac{4(1-\alpha )\beta ^2(1-\beta )}{\alpha ^2},\ \right. \\&\qquad \frac{4(1-\alpha )\beta ^2(1-\beta )}{\alpha ^2},\ \frac{4\beta ^2(1-\beta )^2}{\alpha ^2},\ \frac{4\beta (1-\beta )}{\alpha },\ \frac{4\beta (1-\beta )}{\alpha },\ \\&\qquad \left. \frac{2\beta ^2(1-\beta )^2}{\alpha ^2},\ \frac{4\beta (1-\beta )}{\alpha },\ 1\right) . \end{aligned}$$

Another example is the case of $L=9$ and $m=3$. The size of $\varOmega$ is 84. We define classes of configurations up to cyclic rotation and divide $\varOmega$ into the equivalence classes. The number of the equivalence classes is 10, and their representative elements are

$$\begin{aligned}&000000111,\ 000001011,\ 000001101,\ 000010011,\ 000010101, \\&000011001,\ 000100011,\ 000100101,\ 000101001,\ 001001001. \end{aligned}$$

Thus, a transition matrix is

$$\begin{aligned} \begin{array}{c} 000000111\\ 000001011\\ 000001101\\ \vdots \\ 001001001 \end{array} \left( \begin{array}{ccccc} 1 - \alpha &{} 0 &{} \alpha &{} \ldots &{} 0 \\ (1-\alpha )\beta &{} (1 - \alpha )(1-\beta ) &{} \alpha \beta &{} \ldots &{} 0 \\ 0 &{} (1-\alpha )\beta &{} (1 - \alpha )(1-\beta ) &{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \ldots &{} (1-\alpha )^3+\alpha ^3 \\ \end{array} \right) , \end{aligned}$$

and an eigenvector for eigenvalue 1 is

$$\begin{aligned}&\left( \frac{3(1-\alpha )^4\beta ^2}{\alpha ^2(1-\beta )^2},\ \frac{3(1-\alpha )^3\beta }{\alpha (1-\beta )^2},\ \frac{3(1-\alpha )^3\beta }{\alpha (1-\beta )^2},\ \frac{3(1-\alpha )^2\beta }{\alpha (1-\beta )},\ \frac{3(1-\alpha )^2}{(1-\beta )^2},\right. \\&\qquad \qquad \left. \frac{3(1-\alpha )^2\beta }{\alpha (1-\beta )},\ \frac{3(1-\alpha )^2\beta }{\alpha (1-\beta )},\ \frac{3(1-\alpha )}{1-\beta },\ \frac{3(1-\alpha )}{1-\beta },\ 1\right) . \end{aligned}$$

Examining other concrete examples for small L, we propose a conjecture for the asymptotic distribution of configurations as follows.

• Conjecture: The probability of any configuration $x\in \varOmega$ in the steady state is given by

  $$\begin{aligned} p(x)=C\,\left( \frac{\alpha (1-\beta )}{(1-\alpha )^2 \beta }\right) ^{\#100(x)} \left( \frac{\alpha }{(1-\alpha ) \beta }\right) ^{\#101(x)}, \end{aligned}$$

  (6)

  where C is a normalization constant satisfying $\sum _{x\in \varOmega } p(x)=1$.

By the above conjecture, the probability of x in the steady state of the space size L and the number of particles m is

$$\begin{aligned} p(x)= \frac{ \left( \frac{\alpha (1-\beta )}{(1-\alpha )^2\beta }\right) ^{\#100(x)} \left( \frac{\alpha }{(1-\alpha )\beta }\right) ^{\#101(x)} }{ \sum \limits _{\begin{array}{c} 1\le k_1+k_2\le m\\ 0\le L-m-2k_1-k_2 \end{array}} N(k_1,k_2)\left( \frac{\alpha (1-\beta )}{(1-\alpha )^2\beta }\right) ^{k_1} \left( \frac{\alpha }{(1-\alpha )\beta }\right) ^{k_2} }, \end{aligned}$$

where

$$\begin{aligned} N(k_1,k_2)= \frac{L(L-m-k_1-k_2-1)!(m-1)!}{k_1!k_2!(L-m-2k_1-k_2)!(k_1-1)!(m-k_1-k_2)!}. \end{aligned}$$

Since the mean flux $Q_{L,\alpha ,\beta }(m)$ is an expected value of $(\alpha \#100 + \beta \#101)/L$, it becomes

$$\begin{aligned} Q_{L,\alpha ,\beta }(m) =\frac{1}{L}\frac{ \sum \limits _{\begin{array}{c} 1\le k_1+k_2\le m\\ 0\le L-m-2k_1-k_2 \end{array}} (\alpha k_1+\beta k_2) N(k_1,k_2)\left( \frac{\alpha (1-\beta )}{(1-\alpha )^2\beta }\right) ^{k_1} \left( \frac{\alpha }{(1-\alpha )\beta }\right) ^{k_2} }{\sum \limits _{\begin{array}{c} 1\le k_1+k_2\le m\\ 0\le L-m-2k_1-k_2 \end{array}} N(k_1,k_2)\left( \frac{\alpha (1-\beta )}{(1-\alpha )^2\beta }\right) ^{k_1} \left( \frac{\alpha }{(1-\alpha )\beta }\right) ^{k_2} }. \end{aligned}$$

(7)

Figure 5 shows FD obtained by (7)and that by the numerical calculation. The former is shown by small black circles ($\bullet$) and the latter by white circles ($\bigcirc$). Their good coincidence can be observed from this figure. Although we have not yet obtained the limit distribution as $L \rightarrow \infty$, the profile of Q does not change drastically, for larger L.

Fig. 5

Example of FD. Small black circles ($\bullet$) are obtained by (7) for $L=100$, $\alpha =0.8$, and $\beta =0.1$. White circles ($\bigcirc$) are obtained numerically (for the same L, $\alpha$, and $\beta$) averaged from $n=0$ to 10000

3.2 Extension to 2 types of particles

Let us consider a probabilistic CA defined by the following system of max-plus equations.

$$\begin{aligned}&u_j^{n+1}=u_j^n+q_{j-1}^n-q_{j}^n, \qquad q_j^n=\min (a_j^n, u_{j-1}^n,1-u_j^n, 1-v_j^n), \\&v_j^{n+1}=v_j^n+r_{j-1}^n-r_{j}^n, \qquad r_j^n=\min (b_j^n, v_{j-1}^n,1-v_j^n, 1-u_j^n). \end{aligned}$$

Assume $u_j^n$, $v_j^n \in \{0,1\}$ and probabilistic parameters $a_j^n$ and $b_j^n$ are defined by

$$\begin{aligned} a_j^n= {\left\{ \begin{array}{ll} 1 &{} (\text {prob. }\alpha ) \\ 0 &{} (1-\alpha ) \end{array}\right. },\qquad b_j^n= {\left\{ \begin{array}{ll} 1 &{} (\text {prob. }\beta ) \\ 0 &{} (1-\beta ) \end{array}\right. }. \end{aligned}$$

The above evolution rule can be interpreted as a probabilistic system of two types of particles, considering that $u_j^n$ and $v_j^n$ are the number of particles of type A and B at site j and time n, respectively. Moreover, let us assume these two types of particles do not exist at the same site and at the same time: $(u_j^n,v_j^n)\ne (1,1)$. If we set this condition for the initial data, it is always satisfied during the time evolution according to the above evolution rule. Subsequently, we express the configuration of particles $(u,v)=(0,0)$, (1, 0), and (0, 1) by symbols ${\mathtt{0}}$, ${\mathtt{A}}$, and ${\mathtt{B}}$, respectively. Then, the rule of particle motion is given as the follows:

We call the above system EPBCA2. If $v_j^n\equiv 0$, the motion rule for $u_j^n$ of EPBCA2 reduces to that of PBCA, and that for $v_j^n$ trivial. Thus, PBCA is included in this system as a special case.

Fig. 6

Example of time evolution in the EPBCA2 for $\alpha =0.4$ and $\beta =0.8$. White, grey, and black squares express $(u,v)=(0,0)$ (no particle), (1, 0) (only particle A exists), and (0, 1) (only particle B exists), respectively

Figure 6 shows an example of time evolution in the EPBCA2. Any particle does not pass over the other particles according to the evolution rule. Let us define a “sequence” as an array of particles from a given configuration preserving their relative positions. For example, the sequence in configuration $\mathtt{0AA00BB0}$ is $\mathtt{AABB}$, and this sequence may change into the sequences $\mathtt{BAAB}$, $\mathtt{BBAA}$, and $\mathtt{ABBA}$ during the time evolution. However, sequence $\mathtt{AABB}$ can not change into $\mathtt{ABAB}$ since particles do not pass over one another. Similarly, sequence $\mathtt{ABAB}$ may change into $\mathtt{BABA}$ but not $\mathtt{AABB}$, $\mathtt{BAAB}$, $\mathtt{BBAA}$, or $\mathtt{ABBA}$. If we consider a transition matrix of configurations for given initial data, the configurations are restricted to those obtained from the initial data. Therefore, if a set of configurations $\varOmega$ includes a configuration $x=x_1x_2\ldots x_L$, we restrict $\varOmega$ to be constructed from any combination of $\mathtt{0}$’s, $\mathtt{A}$’s, and $\mathtt{B}$’s preserving their numbers and the order of sequence included in x up to cyclic rotation. Subsequently, we give two examples of transition matrices and their eigenvectors.

The first example is $\varOmega$ that includes configuration $\mathtt{AABAAB00}$. The size of $\varOmega$ is 84. To make the expression of the transition matrix compact, we define classes of configurations up to cyclic rotation and divide $\varOmega$ into the equivalence classes. The number of equivalence classes is 12, and their representative elements are as follows:

$$\begin{aligned}&\mathtt{00AABAAB},\ \mathtt{0A0ABAAB},\ \mathtt{0AA0BAAB},\ \mathtt{0AAB0AAB},\ \mathtt{0AABA0AB},\ \mathtt{0AABAA0B}, \\&\mathtt{A00ABAAB},\ \mathtt{A0A0BAAB},\ \mathtt{A0ABA0AB},\ \mathtt{A0ABAA0B},\ \mathtt{AA00BAAB},\ \mathtt{AA0BAA0B}. \end{aligned}$$

The transition matrix derived by transition probabilities from each representative element to the others is

$$\begin{aligned} \begin{array}{c} \mathtt{00AABAAB}\\ \mathtt{0A0ABAAB}\\ \mathtt{0AA0BAAB}\\ \vdots \\ \mathtt{AA0BAA0B}\end{array} \left( \begin{array}{ccccc} 1-\beta &{} 0 &{} 0 &{} \ldots &{} 0 \\ \alpha (1-\beta ) &{} (1-\alpha )(1-\beta ) &{} 0 &{} \ldots &{} 0 \\ 0 &{} \alpha (1-\beta ) &{} (1-\alpha )(1-\beta ) &{} \ldots &{} (1-\alpha )\beta \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \ldots &{} (1-\alpha )^2 \\ \end{array} \right) , \end{aligned}$$

and its eigenvector for eigenvalue 1 is

$$\begin{aligned}&\left( \frac{8\alpha ^2 (1-\beta )}{(1-\alpha )^2 \beta ^2},\ \frac{8\alpha }{(1-\alpha )^2 \beta },\ \frac{8\alpha }{(1-\alpha )^2 \beta },\ \frac{4\alpha ^2}{(1-\alpha )^2 \beta ^2},\ \frac{8\alpha }{(1-\alpha )^2 \beta },\ \frac{8\alpha }{(1-\alpha )^2 \beta },\right. \\&\quad \left. \frac{8}{1-\alpha },\ \frac{8}{(1-\alpha )^2},\ \frac{4}{(1-\alpha )^2},\ \frac{8}{(1-\alpha )^2},\ \frac{8}{1-\alpha },\ \frac{4}{(1-\alpha )^2} \right) . \end{aligned}$$

Another example is $\varOmega$ that includes configuration $\mathtt{AABA000}$. The size of $\varOmega$ is 140, the number of equivalence classes is 20, and their representative elements are

$$\begin{aligned}&\mathtt{000AABA},\ \mathtt{00A0ABA},\ \mathtt{00AA0BA},\ \mathtt{00AAB0A},\ \mathtt{0A00ABA},\ \mathtt{0A0A0BA}, \\&\mathtt{0A0AB0A},\ \mathtt{0AA00BA},\ \mathtt{0AA0B0A},\ \mathtt{0AAB00A},\ \mathtt{A000ABA},\ \mathtt{A00A0BA}, \\&\mathtt{A00AB0A},\ \mathtt{A0A00BA},\ \mathtt{A0A0B0A},\ \mathtt{A0AB00A},\ \mathtt{AA000BA},\ \mathtt{AA0B0A}, \\&\mathtt{AA0B00A},\ \mathtt{AAB000A}. \end{aligned}$$

The transition matrix is

$$\begin{aligned} \begin{array}{c} \mathtt{000AABA}\\ \mathtt{00A0ABA}\\ \mathtt{00AA0BA}\\ \vdots \\ \mathtt{AAB000A}\end{array} \left( \begin{array}{ccccc} 1-\alpha &{} 0 &{} 0 &{} \ldots &{} 0 \\ \alpha (1-\alpha ) &{} (1-\alpha )^2 &{} 0 &{} \ldots &{} 0 \\ 0 &{} \alpha (1-\alpha ) &{} (1-\alpha )^2 &{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \ldots &{} 1-\beta \\ \end{array} \right) , \end{aligned}$$

and the eigenvector for eigenvalue 1 is

$$\begin{aligned}&\left( \frac{1}{1-\alpha }, \frac{1}{(1-\alpha )^2}, \frac{1}{(1-\alpha )^2}, \frac{\alpha }{(1-\alpha )^2 \beta }, \frac{1}{(1-\alpha )^2}, \frac{1}{(1-\alpha )^3}, \frac{\alpha }{(1-\alpha )^3 \beta }, \right. \\&\qquad \frac{1}{(1-\alpha )^2}, \frac{\alpha }{(1-\alpha )^3 \beta }, \frac{\alpha ^2 (1-\beta )}{(1-\alpha )^3 \beta ^2}, \frac{1}{1-\alpha }, \frac{1}{(1-\alpha )^2}, \frac{\alpha }{(1-\alpha )^2 \beta }, \frac{1}{(1-\alpha )^2},\\&\qquad \left. \frac{\alpha }{(1-\alpha )^3 \beta }, \frac{\alpha ^2 (1-\beta )}{(1-\alpha )^3 \beta ^2}, \frac{1}{1-\alpha }, \frac{\alpha }{(1-\alpha )^2 \beta }, \frac{\alpha ^2 (1-\beta )}{(1-\alpha )^3 \beta ^2}, \frac{\alpha ^3 (1-\beta )^2}{(1-\alpha )^3 \beta ^3} \right) . \end{aligned}$$

Examining other concrete examples for small L, we propose a conjecture for the asymptotic distribution of configurations. Before giving the conjecture, we set the notations. Assume the space size is L and the number of particles of type A and B are $m_\mathtt{A}$ and $m_\mathtt{B}$, respectively. If we choose a certain configuration, a set $\varOmega$ of configurations is defined by all realizable configurations evolving from it. Let $x=x_1 x_2\ldots x_L$ be one of configurations in $\varOmega$. Let $k_\mathtt{A}$ and $k_\mathtt{B}$ be the number of local patterns $\mathtt{A0}$ and $\mathtt{B0}$ included in x, respectively. Let $n_\mathtt{A}$ be the number of all 0’s in the local patterns $\mathtt{A0}\ldots \mathtt{0B}$ and $\mathtt{A0}\ldots \mathtt{0A}$, and let $n_\mathtt{B}$ be that of $\mathtt{B0}\ldots \mathtt{0A}$ and $\mathtt{B0}\ldots \mathtt{0B}$. For example, if configuration

$$\begin{aligned} \mathtt{BAAA00A0B0BB00A000} \end{aligned}$$

is given, then $k_\mathtt{A}=5$, $k_\mathtt{B}=4$, $n_\mathtt{A}=6$, and $n_\mathtt{B}=3$. Note that $m_\mathtt{A}+m_\mathtt{B}+n_\mathtt{A}+n_\mathtt{B}=L$. Using these notations, we introduce the following conjecture.

• Conjecture: The probability of configuration x in the steady state is

  $$\begin{aligned} p(x) = C\,\frac{(1-\beta )^{n_\mathtt{B}-k_\mathtt{B}}}{(1-\alpha )^{k_\mathtt{A}+n_\mathtt{B}}} \left( \frac{\alpha }{\beta }\right) ^{n_\mathtt{B}}, \end{aligned}$$

  where C is a normalization constant satisfying $\sum _{x\in \varOmega } p(x)=1$.

From the above conjecture, the probability of any configuration x for $k_\mathtt{A}$, $k_\mathtt{B}$, $n_\mathtt{A}$, and $n_\mathtt{B}$ in the steady state is given by

$$\begin{aligned} p(x)= \frac{ \frac{(1-\beta )^{n_\mathtt{B}-k_\mathtt{B}}}{(1-\alpha )^{k_\mathtt{A}+n_\mathtt{B}}} \left( \frac{\alpha }{\beta }\right) ^{n_\mathtt{B}} }{\sum \limits _{\begin{array}{c} k_\mathtt{A}\le \min (n_\mathtt{A}, m_\mathtt{A}),\\ k_\mathtt{B}\le \min (n_\mathtt{B}, m_\mathtt{B}),\\ n_\mathtt{A}+n_\mathtt{B}=L-m_\mathtt{A}-m_\mathtt{B} \end{array}} N(k_\mathtt{A},k_\mathtt{B},n_\mathtt{A},n_\mathtt{B}) \frac{(1-\beta )^{n_\mathtt{B}-k_\mathtt{B}}}{(1-\alpha )^{k_\mathtt{A}+n_\mathtt{B}}} \left( \frac{\alpha }{\beta }\right) ^{n_\mathtt{B}}}, \end{aligned}$$

(8)

where $N(k_\mathtt{A}, k_\mathtt{B}, n_\mathtt{A}, n_\mathtt{B})$ denotes the number of all configurations included in $\varOmega$ with $k_\mathtt{A}$, $k_\mathtt{B}$, $n_\mathtt{A}$, and $n_\mathtt{B}$ and is calculated as

$$\begin{aligned}&N(k_\mathtt{A},k_\mathtt{B},n_\mathtt{A},n_\mathtt{B}) \\&\quad = \displaystyle \frac{L\cdot (m_\mathtt{A}-1)!(n_\mathtt{A}-1)!(m_\mathtt{B}-1)!(n_\mathtt{B}-1)!}{(m_\mathtt{A}-k_\mathtt{A})!k_\mathtt{A}!(n_\mathtt{A}-k_\mathtt{A})!(k_\mathtt{A}-1)!(m_\mathtt{B}-k_\mathtt{B})!k_\mathtt{B}!(n_\mathtt{B}-k_\mathtt{B})!(k_\mathtt{B}-1)!}, \end{aligned}$$

Considering the motion rule of particles A and B, the flux in the steady state is

$$\begin{aligned} Q_{L,\alpha ,\beta }(m_\mathtt{A},m_\mathtt{B})= \frac{ \sum \nolimits _{\begin{array}{c} k_\mathtt{A}\le \min (n_\mathtt{A}, m_\mathtt{A}),\\ k_\mathtt{B}\le \min (n_\mathtt{B}, m_\mathtt{B}),\\ n_\mathtt{A}+n_\mathtt{B}=L-m_\mathtt{A}-m_\mathtt{B} \end{array}} \frac{\alpha k_\mathtt{A}+\beta k_\mathtt{B}}{L} N(k_\mathtt{A}, k_\mathtt{B}, n_\mathtt{A}, n_\mathtt{B}) \frac{(1-\beta )^{n_\mathtt{B}-k_\mathtt{B}}}{(1-\alpha )^{k_\mathtt{A}+n_\mathtt{B}}} \left( \frac{\alpha }{\beta }\right) ^{n_\mathtt{B}} }{ \sum \nolimits _{\begin{array}{c} k_\mathtt{A}\le \min (n_\mathtt{A}, m_\mathtt{A}),\\ k_\mathtt{B}\le \min (n_\mathtt{B}, m_\mathtt{B}),\\ n_\mathtt{A}+n_\mathtt{B}=L-m_\mathtt{A}-m_\mathtt{B} \end{array}} N(k_\mathtt{A},k_\mathtt{B},n_\mathtt{A},n_\mathtt{B}) \frac{(1-\beta )^{n_\mathtt{B}-k_\mathtt{B}}}{(1-\alpha )^{k_\mathtt{A}+n_\mathtt{B}}} \left( \frac{\alpha }{\beta }\right) ^{n_\mathtt{B}} }. \end{aligned}$$

(9)

Figure 7a shows FD calculated by (9) and Fig. 7b shows the numerical result. In these figures, $\rho _A$ and $\rho _B$ are densities of particles A and B, respectively.

Fig. 7

Example of FD. a Theoretical result by (9) for $L=30$, $\alpha =0.3$, and $\beta =0.6$. b Numerical result averaged from $n=0$ to $n=$ 100,000 with the same parameters as in a

Figure 8 shows a comparison of FDs of Fig. 7 for $\rho _\mathtt{B}=0.5$. Small black circles ($\bullet$) are obtained by (9) and white circles ($\bigcirc$) by the numerical calculation. Their good coincidence can be observed from this figure.

Fig. 8

Example of FD for $\rho _\mathtt{B}=0.5$. Small black circles ($\bullet$) are obtained by (9) for $L=30$, $\alpha =0.3$, and $\beta =0.6$. White circles ($\bigcirc$) are obtained numerically for the same L, $\alpha$, and $\beta$ averaged from $n=0$ to 100,000

4 Concluding remarks

We introduced some conjectures on the asymptotic distribution of PBCA and its extensions, assuming that these systems are ergodic. In the conjectures, the following points are the most important.

• Probability of any configuration in the steady state depends only on the number of some specific local patterns included in the configuration. For example, it depends only on $\#10$ for PBCA.

• Since the probabilities do not depend on the location of patterns in the configuration, they are equal to each other if the numbers of patterns included in the configurations are also equal. For example, the probabilities of configurations are the same if their $\#10$ are the same in the case of PBCA.

Based on the conjecture, we derived the probability of configuration in the steady state and FD of the system for arbitrary size of L.

On the other hand, FD of PBCA for $L\rightarrow \infty$ is reported in the previous research as

$$\begin{aligned} Q=\frac{1-\sqrt{1-4\alpha \rho (1-\rho )}}{2}, \end{aligned}$$

using an ansatz on relations of probabilities of local patterns [11]. Using the GKZ hypergeometric function, we evaluate the limit of FD of PBCA (3) and confirm that the diagram coincides with the above result.

Furthermore, since FD of the extended systems is also expressed by some kind of the GKZ hypergeometric function, we expect that FD in the limit of infinite size can be derived similarly as PBCA. In particular, for EPBCA2, for the initial condition of sequence $\ldots \mathtt{ABABABAB}\ldots$ and a probabilistic parameter $\alpha =1$, the rule of particle motion in the steady state becomes as follows.

This motion rule is the same as that of the L-R system obtained by the ultradiscrete Cole–Hopf transformation of SECA84 with a quadratic conserved quantity [14]. The FD of L-R system in the limit of infinite space size is evaluated and derived in a simple form depending on the density of particles. Therefore, FD of EPBCA2 in the limit of $L\rightarrow \infty$ includes FD of SPCA84 as a special case.

Limit of FD of PBCA using the GKZ hypergeometric function

1.1 Definition of the GKZ hypergeometric function and its properties

In this section, we define the GKZ hypergeometric function and its properties. First, let us define $B_{k}^{\gamma }(x)$ by

$$\begin{aligned} B_{k}^{\gamma }(x)=\frac{x^{\gamma +k}}{\varGamma (\gamma +k+1)}. \end{aligned}$$

It satisfies the following contiguity relations.

$$\begin{aligned} \frac{d}{dx}B_{k}^{\gamma }(x)& = B_{k-1}^{\gamma }(x)=B_{k}^{\gamma -1}(x),\\ x B_{k}^{\gamma }(x)& = (\gamma +k+1)B_{k+1}^{\gamma }(x)=(\gamma +k+1)B_{k}^{\gamma +1}(x). \end{aligned}$$

For an $m\times n$ matrix $A=(a_{ij})$ and an n-dimensional vector $\mathbf {\beta }$, general solution to

$$\begin{aligned} A\mathbf {\gamma }=\mathbf {\beta }, \end{aligned}$$

is expressed by

$$\begin{aligned} \mathbf {\gamma }=\mathbf {\gamma _0}+\mathbf {k}, \quad \mathbf {k}\in \ker A, \end{aligned}$$

where $\mathbf {\gamma _0}$ is a special solution to the equation. Using A, $\mathbf {\beta }$, $\mathbf {\gamma _0}$ and $\mathbf {k}$, the GKZ hypergeometric function $\varphi (\mathbf {\beta };\mathbf {x})$ is defined by

$$\begin{aligned} \varphi (\mathbf {\beta };\mathbf {x})=\sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^n} \prod _{j=1}^{n} B_{k_j}^{\gamma _{0,j}}(x_j), \end{aligned}$$

(10)

where $\mathbf {x}$ is an n-dimensional vector and $\gamma _{0,j}$, $k_j$ and $x_j$ are jth element of $\mathbf {\gamma _0}$ , $\mathbf {k}$, and $\mathbf {x}$, respectively. Although $\varphi$ also depends on the matrix A, A is fixed below and we omit the dependency. Using contiguity relations, the following two properties for GKZ hypergeometric function are derived.

First, for a given vector

$$\begin{aligned} \mathbf {b}= \left( \begin{array}{c} b_1\\ b_2\\ \vdots \\ b_n \end{array} \right) \in \ker A \cap \mathbb {Z}^n, \end{aligned}$$

$J_{+}(\mathbf {b})$ and $J_{-}(\mathbf {b})$ are defined by subsets of $\{0,1,\ldots ,n \}$ as

$$\begin{aligned} J_{+}(\mathbf {b})=\{j|b_j > 0 \} ,\qquad J_{-}(\mathbf {b})= \{j|b_j < 0\}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \prod _{j \in J_{-}(\mathbf {b})} \left( \frac{\partial }{\partial x_j}\right) ^{-b_j}\varphi& = \sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^n} \prod _{j \in J_{-}(\mathbf {b})} \left( \frac{\partial }{\partial x_j}\right) ^{-b_j} \prod _{j=1}^n B_{k_j}^{\gamma _{0,j}}(x_j) \\& = \sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^n} \prod _{j \in J_{+}(\mathbf {b})} B_{k_j}^{\gamma _{0,j}}(x_j) \prod _{j \in J_{-}(\mathbf {b})} B_{k_j+b_j}^{\gamma _{0,j}}(x_j) \\& = \sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^n} \prod _{j \in J_{+}(\mathbf {b})} \left( \frac{\partial }{\partial x_j}\right) ^{b_j} \prod _{j=1}^n B_{k_j}^{\gamma _{0,j}}(x_j) \\& = \prod _{j \in J_{+}(\mathbf {b})} \left( \frac{\partial }{\partial x_j}\right) ^{b_j}\varphi . \end{aligned}$$

Therefore, $\varphi$ satisfies a differential equation

$$\begin{aligned} \left\{ \prod _{j \in J_{+}(\mathbf {b})} \left( \frac{\partial }{\partial x_j}\right) ^{b_j}-\prod _{j \in J_{-}(\mathbf {b})} \left( \frac{\partial }{\partial x_j}\right) ^{-b_j} \right\} \varphi =0. \end{aligned}$$

(11)

Second, for an operator $\theta _j=x_j\frac{\partial }{\partial x_j}$ and $\mathbf {\theta }$ defined by

$$\begin{aligned} \mathbf {\theta }= \left( \begin{array}{c} \theta _1\\ \theta _2\\ \vdots \\ \theta _n \end{array} \right) , \end{aligned}$$

$\varphi$ satisfies

$$\begin{aligned} A\mathbf {\theta }\varphi (\mathbf {\beta };\mathbf {x}) =A(\mathbf {\gamma }+\mathbf {k})\varphi =\mathbf {\beta }\varphi . \end{aligned}$$

Using $\alpha \in \mathbb {C}^{\times }$ and the ith row vector $\mathbf {a_i}=(a_{i1},\ldots ,a_{in})$ of A, define $\alpha ^{D(\mathbf {a_i})}$ by

$$\begin{aligned} \alpha ^{D(\mathbf {a_i})}= \hbox {diag}(\alpha ^{a_{i1}},\ldots ,\alpha ^{a_{in}}). \end{aligned}$$

Since

$$\begin{aligned} B_{k_j}^{\gamma _j} (\alpha ^{a_{ij}} x_j) = \alpha ^{a_{ij} (\gamma _j + k_j)} B_{k_j}^{\gamma _j}(x_j), \end{aligned}$$

$B_{k_j}^{\gamma _j} (x_j)$ satisfies

$$\begin{aligned} \prod _{j=1}^{n}B_{k_j}^{\gamma _j} (\alpha ^{a_{ij}} x_j) = \alpha ^{\sum _{j=1}^{n}a_{ij} (\gamma _j + k_j)} \prod _{j=1}^{n} B_{k_j}^{\gamma _j}(x_j) = \alpha ^{\beta _i} \prod _{j=1}^{n} B_{k_j}^{\gamma _j}(x_j). \end{aligned}$$

Thus,

$$\begin{aligned} \varphi (\mathbf {\beta };\alpha ^{D(\mathbf {a_i})} \mathbf {x}) = \alpha ^{\beta _i}\varphi (\mathbf {\beta };\mathbf {x}), \end{aligned}$$

(12)

is obtained.

1.2 FD of PBCA expressed by the GKZ hypergeometric function

In this subsection, we express FD of PBCA by the GKZ hypergeometric function. The FD of PBCA (3) for the infinite space size is

$$\begin{aligned} Q=\lim _{\begin{array}{c} L\rightarrow \infty \\ m=\rho L \end{array}}Q_{L,\alpha }(m)=\lim _{\begin{array}{c} L\rightarrow \infty \\ m=\rho L \end{array}}\frac{\alpha }{L}\frac{\sum _{k=1}^{m} k \left( \frac{1}{1-\alpha }\right) ^{k-1} N_{L,m}(k)}{\sum _{k=1}^{m} \left( \frac{1}{1-\alpha }\right) ^{k-1} N_{L,m}(k)}, \end{aligned}$$

where density $\rho$ is constant and

$$\begin{aligned} N_{L,m}(k)=\frac{(m-1)!L(L-m-1)! }{(m-k)!(k-1)!k! (L-m-k)!}. \end{aligned}$$

To evaluate the above limit, we choose the following matrix A and vector $\mathbf {\beta _1}$ in the definition of the GKZ hypergeometric function in A.1.

$$\begin{aligned} A = \left( \begin{array}{cccc} 0 &{} -1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 0 \end{array} \right) , \qquad \mathbf {\beta _1}= \left( \begin{array}{c} 1\\ L-1\\ m \end{array} \right) . \end{aligned}$$

The general solution to $A \mathbf {\gamma }=\mathbf {\beta _1}$ is

$$\begin{aligned} \mathbf {\gamma }=\mathbf {\gamma _0}+\mathbf {k}\qquad (\mathbf {k}\in \ker A \cap \mathbb {Z}^4 ), \end{aligned}$$

where

$$\begin{aligned} \mathbf {\gamma _0}= \left( \begin{array}{c} \gamma _{0,1}\\ \gamma _{0,2}\\ \gamma _{0,3}\\ \gamma _{0,4}\\ \end{array} \right) = \left( \begin{array}{c} m\\ -1\\ 0 \\ L-m \end{array} \right) , \qquad \mathbf {k}= \left( \begin{array}{c} k_{1}\\ k_{2}\\ k_{3}\\ k_{4}\\ \end{array} \right) = k \left( \begin{array}{c} -1\\ 1\\ 1 \\ -1 \end{array} \right) \quad (k\in \mathbb {Z}). \end{aligned}$$

(13)

The form of A is chosen to give $\mathbf {\gamma }$ of which elements corresponding to the variables of factorials in the denominator of $N_{L,m}(k)$. Introducing a new notation $\varphi _{\beta _1, \beta _2, \beta _3}(x_1, x_2, x_3, x_4)$ defined by $\varphi (\mathbf {k}, \mathbf {x})$ for $\mathbf {\beta }=(\beta _1, \beta _2, \beta _3)$ and $\mathbf {x}=(x_1, x_2, x_3, x_4)$ and $\lambda$ by $1/(1-\alpha )$, we obtain

$$\begin{aligned} \varphi _{1,L-1,m}(1,\lambda ,1,1)& = \sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^4} B_{k_1}^{\gamma _{0,1}}(1) B_{k_2}^{\gamma _{0,2}}(\lambda ) B_{k_3}^{\gamma _{0,3}}(1) B_{k_4}^{\gamma _{0,4}}(1) \\& = \sum _{k=1}^{m} \frac{\lambda ^{k-1}}{(m-k)! (k-1)! k! (L-m-k)!}. \end{aligned}$$

Considering $\varphi _{\beta _1, \beta _2, \beta _3}(1,\lambda ,1,1)$ as the function on $\lambda$, let us introduce a notation $F_{\beta _1, \beta _2, \beta _3}(\lambda )=\varphi _{\beta _1, \beta _2, \beta _3}(1,\lambda ,1,1)$.

On the other hand, the general solution to $A \mathbf {\gamma '}=\mathbf {\beta _2}$ for

$$\begin{aligned} \mathbf {\beta _2}= \left( \begin{array}{c} 0\\ L-2\\ m-1 \end{array} \right) , \end{aligned}$$

is

$$\begin{aligned} \mathbf {\gamma '}=\mathbf {\gamma '_0}+\mathbf {k}\qquad (\mathbf {k}\in \ker A \cap \mathbb {Z}^4 ), \end{aligned}$$

where

$$\begin{aligned} \mathbf {\gamma '_0}= \left( \begin{array}{c} \gamma '_{0,1}\\ \gamma '_{0,2}\\ \gamma '_{0,3}\\ \gamma '_{0,4}\\ \end{array} \right) = \left( \begin{array}{c} m\\ -1\\ -1 \\ L-m \end{array} \right) . \end{aligned}$$

(14)

Therefore,

$$\begin{aligned} \varphi _{0,L-2,m-1}(1,\lambda ,1,1)& = \sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^4} B_{k_1}^{\gamma '_{0,1}}(1) B_{k_2}^{\gamma '_{0,2}}(\lambda ) B_{k_3}^{\gamma '_{0,3}}(1) B_{k_4}^{\gamma '_{0,4}}(1) \\& = \sum _{k=1}^{m} \frac{\left( \frac{1}{1-\alpha }\right) ^{k-1}}{(m-k)! (k-1)! (k-1)! (L-m-k)!} \\& = F_{0,L-2,m-1}(\lambda ), \end{aligned}$$

is obtained. Thus, we have

$$\begin{aligned} Q=\lim _{\begin{array}{c} L\rightarrow \infty \\ m=\rho L \end{array}}\frac{\alpha }{L}\frac{F_{0,L-2,m-1}(\lambda )}{F_{1,L-1,m}(\lambda )}. \end{aligned}$$

(15)

1.3 Differential equation on $F_{1,L-1,m}$

In this section, we derive a differential equation on $F_{1,L-1,m}$. Since the relations

$$\begin{aligned} \varphi _{1,L-1,m}\bigg (x_1, \frac{x_2}{a}, a x_3, x_4\bigg )& = a \varphi _{1,L-1,m}(x_1,x_2,x_3,x_4), \\ \varphi _{1,L-1,m}(b x_1, b x_2, b x_3, b x_4)& = b^{L-1}\varphi _{1,L-1,m}(x_1,x_2,x_3,x_4), \\ \varphi _{1,L-1,m}(c x_1, x_2, c x_3, x_4)& = c^m \varphi _{1,L-1,m}(x_1,x_2,x_3,x_4), \end{aligned}$$

for $\varphi _{1,L-1,m}(x_1,x_2,x_3,x_4)$ and a, b ,$c \in \mathbb {C}^{\times }$ are obtained from (12), the relation

$$\begin{aligned} \varphi _{1,L-1,m}\bigg (bc x_1,\frac{b}{a}x_2,abc x_3,b x_4\bigg )=ab^{L-1} c^{m} \varphi _{1,L-1,m}(x_1,x_2,x_3,x_4), \end{aligned}$$

holds. If we assume

$$\begin{aligned} \bigg (bc x_1,\frac{b}{a}x_2,abc x_3,b x_4\bigg )=(1,\lambda ,1,1), \end{aligned}$$

that is,

$$\begin{aligned} a=\frac{x_1}{x_3},\quad b=\frac{1}{x_4},\quad c=\frac{x_4}{x_1},\quad \lambda =\frac{x_2 x_3}{x_1 x_4}, \end{aligned}$$

(16)

the relation between $\varphi _{1,L-1,m}$ and $F_{1,L-1,m}$ is

$$\begin{aligned} \varphi _{1,L-1,m}(x_1,x_2,x_3,x_4)=x_1^{m-1} x_3 x_4^{L-m-1} F_{1,L-1,m}(\lambda ). \end{aligned}$$

(17)

Moreover, we can derive

$$\begin{aligned} \frac{\partial ^2}{\partial x_2 \partial x_3} \varphi _{1,L-1,m}& = 2x_1^{m-2} x_3 x_4^{L-m-2} F'_{1,L-1,m}(\lambda )+x_1^{m-3} x_2 x_3^2 x_4^{L-m-3} F''_{1,L-1,m}(\lambda ), \\ \frac{\partial ^2}{\partial x_1 \partial x_4} \varphi _{1,L-1,m}& = (m-1)(L-m-1)x_1^{m-2} x_3 x_4^{L-m-2}F_{1,L-1,m}(\lambda ) \\&-(L-m-1)x_1^{m-3} x_2 x_3^2 x_4^{L-m-3} F'_{1,L-1,m}(\lambda ) \\&-(m-2)x_1^{m-3} x_2 x_3^2 x_4^{L-m-3} F'_{1,L-1,m}(\lambda ) \\&+x_1^{m-4} x_2^2 x_3^3 x_4^{L-m-4} F''_{1,L-1,m}(\lambda ). \end{aligned}$$

Substituting these equations into the differential equation

$$\begin{aligned} \left( \frac{\partial ^2}{\partial x_2 \partial x_3} - \frac{\partial ^2}{\partial x_1 \partial x_4}\right) \varphi _{1,L-1,m}=0, \end{aligned}$$

which is derived from (11), the following differential equation on $F_{1,L-1,m}$ is obtained.

$$\begin{aligned}&\lambda (1-\lambda ) F''_{1,L-1,m}(\lambda )+\{ (L-3)\lambda +2 \} F'_{1,L-1,m}(\lambda ) \nonumber \\&\qquad \qquad -(m-1)(L-m-1) F_{1,L-1,m}(\lambda )=0. \end{aligned}$$

(18)

1.4 Contiguity relation between $F_{1,L-1,m}$ and $F_{0,L-2,m-1}$

From (13) and (14), we have

$$\begin{aligned} \mathbf {\gamma '}-\mathbf {\gamma }= \left( \begin{array}{c} 0\\ 0\\ -1 \\ 0 \end{array} \right) +k \left( \begin{array}{c} -1\\ 1\\ 1 \\ -1 \end{array} \right) \qquad (k\in \mathbb {Z}). \end{aligned}$$

Therefore,

$$\begin{aligned} \varphi _{0,L-2,m-1}(x_1,x_2,x_3,x_4)& = \sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^4} B_{k_1}^{\gamma '_{0,1}}(x_1) B_{k_2}^{\gamma '_{0,2}}(x_2) B_{k_3}^{\gamma '_{0,3}}(x_3) B_{k_4}^{\gamma '_{0,4}}(x_4) \nonumber \\& = \sum _{\mathbf {k}\in \ker A \cap \mathbb {Z}^4} B_{k_1}^{\gamma _{0,1}}(x_1) B_{k_2}^{\gamma _{0,2}}(x_2) B_{k_3}^{\gamma _{0,3}-1}(x_3) B_{k_4}^{\gamma _{0,4}}(x_4) \nonumber \\& = \frac{\partial }{\partial x_3} \varphi _{1,L-1,m}(x_1,x_2,x_3,x_4), \end{aligned}$$

(19)

is derived. From (12), since the relations

$$\begin{aligned} \varphi _{0,L-2,m-1}\left( x_1,\frac{1}{a}x_2,a x_3, x_4\right)& = \varphi _{0,L-2,m-1}(x_1,x_2,x_3,x_4), \\ \varphi _{0,L-2,m-1}(bx_1,bx_2,bx_3,bx_4)& = b^{L-2}\varphi _{0,L-2,m-1}(x_1,x_2,x_3,x_4), \\ \varphi _{0,L-2,m-1}(c x_1,x_2,c x_3,x_4)& = c^{m-1} \varphi _{0,L-2,m-1}(x_1,x_2,x_3,x_4), \end{aligned}$$

are obtained, the relation

$$\begin{aligned} \varphi _{0,L-2,m-1}\left( bc x_1,\frac{b}{a}x_2,abc x_3,b x_4\right) = b^{L-2} c^{m-1} \varphi _{0,L-2,m-1}(x_1,x_2,x_3,x_4), \end{aligned}$$

holds. Substituting (16) into this equation, we have

$$\begin{aligned} \varphi _{0,L-2,m-1}(x_1,x_2,x_3,x_4)=x_1^{m-1} x_4^{L-m-1} F_{0,L-2,m-1}(\lambda ). \end{aligned}$$

(20)

Thus, we obtain

$$\begin{aligned} x_1^{m-1} x_4^{L-m-1} F_{0,L-2,m-1}(\lambda )=\frac{\partial }{\partial x_3} \varphi _{1,L-1,m}(x_1,x_2,x_3,x_4), \end{aligned}$$

(21)

from (19) and (20).

On the other hand, derivative of (17) with respect to $x_3$ is

$$\begin{aligned}&\frac{\partial }{\partial x_3} \varphi _{1,L-1,m}(x_1,x_2,x_3,x_4) \nonumber \\&\quad =x_1^{m-1}x_4^{L-m-1} F_{1,L-1,m}(\lambda )+x_1^{m-2} x_2 x_3 x_4^{L-m-2} F'_{1,L-1,m}(\lambda ). \end{aligned}$$

(22)

Therefore, from (21) and (22),

$$\begin{aligned} F_{0,L-2,m-1}(\lambda )=F_{1,L-1,m}(\lambda )+\lambda F'_{1,L-1,m}(\lambda ), \end{aligned}$$

(23)

is obtained. Derivative of (23) with respect to $\lambda$ is

$$\begin{aligned} F'_{0,L-2,m-1}(\lambda )= 2F'_{1,L-1,m}(\lambda ) + \lambda F''_{1,L-1,m}(\lambda ). \end{aligned}$$

(24)

Substituting (18) into (24) gives

$$\begin{aligned} F'_{0,L-2,m-1}(\lambda )=\frac{(m-1)(L-m-1)}{1-\lambda } F_{1,L-1,m}(\lambda )-\frac{(L-1)\lambda }{1-\lambda }F'_{1,L-1,m}(\lambda ). \end{aligned}$$

(25)

From (23) and (25), contiguity relation between $F_{1,L-1,m}$ and $F_{0,L-2,m-1}$ is

$$\begin{aligned} \left( \begin{array}{c} F_{0,L-2,m-1}(\lambda )\\ F_{0,L-2,m-1}'(\lambda ) \end{array} \right) = \left( \begin{array}{cc} 1 &{} \lambda \\ \frac{(m-1)(L-m-1)}{1-\lambda } &{} \frac{(L-1)\lambda }{1-\lambda } \end{array} \right) \left( \begin{array}{c} F_{1,L-1,m}(\lambda )\\ F_{1,L-1,m}'(\lambda ) \end{array} \right) . \end{aligned}$$

(26)

1.5 Limit of contiguity relation

From the contiguity relation (26), we have

$$\begin{aligned} \left( \begin{array}{c} F_{0,L-2,m-1}(\lambda )\\ \frac{F'_{0,L-2,m-1}(\lambda )}{m} \end{array} \right) = \left( \begin{array}{cc} 1 &{} \lambda m \\ \frac{(m-1)(L-m-1)}{(1-\lambda ) m} &{} \frac{(L-1)\lambda }{1-\lambda } \end{array} \right) \left( \begin{array}{c} F_{1,L-1,m}(\lambda )\\ \frac{F'_{1,L-1,m}(\lambda )}{m} \end{array} \right) . \end{aligned}$$

(27)

Dividing both side of (27) by $LF_{1,L-1,m}(\lambda )$,

$$\begin{aligned} \left( \begin{array}{c} \frac{F_{0,L-2,m-1}(\lambda )}{L F_{1,L-1,m}(\lambda )}\\ \frac{F'_{0,L-2,m-1}(\lambda )}{m L F_{1,L-1,m}(\lambda )} \end{array} \right) = \left( \begin{array}{cc} \frac{1}{L} &{} \frac{\lambda m}{L} \\ \frac{(m-1)(L-m-1)}{(1-\lambda ) m L} &{} \frac{(L-1)\lambda }{(1-\lambda ) L} \end{array} \right) \left( \begin{array}{c} 1\\ \frac{F'_{1,L-1,m}(\lambda )}{m F_{1,L-1,m}(\lambda )} \end{array} \right) , \end{aligned}$$

(28)

is obtained. If we define

$$\begin{aligned} g=\frac{F'_{1,L-1,m}(\lambda )}{F_{1,L-1,m}(\lambda )}, \end{aligned}$$

and substitute g into (18), we obtain

$$\begin{aligned} \lambda (1-\lambda )(g'+g^2)+\{ (L-3)\lambda +2 \} g-(m-1)(L-m-1)=0. \end{aligned}$$

Since $\rho =m/L$, we have

$$\begin{aligned} \lambda (1-\lambda )(g'+g^2)+\left\{ \left( \frac{m}{\rho }-3\right) \lambda +2 \right\} g-(m-1)\left( \frac{m}{\rho }-m-1\right) =0. \end{aligned}$$

(29)

We can assume the following expansion of g for $m=\infty$:

$$\begin{aligned} g=g_1 m+g_0 + g_{-1}m^{-1} +g_{-2}m^{-2} +\cdots . \end{aligned}$$

From the balance of ${\mathcal {O}}(m^2)$ terms of (29), we have

$$\begin{aligned} \lambda (1-\lambda )g_1^2+\frac{\lambda }{\rho }g_1+1-\frac{1}{\rho }=0. \end{aligned}$$

Solving this relation,

$$\begin{aligned} g_1=\frac{-\frac{\lambda }{\rho }-\sqrt{\left( \frac{\lambda }{\rho }\right) ^2-4\lambda (1-\lambda )\left( 1-\frac{1}{\rho }\right) }}{2\lambda (1-\lambda )}, \end{aligned}$$

(30)

is obtained. Therefore, we can derive the limit of the first component of (28) using $g_1$ as

$$\begin{aligned} \lim _{\begin{array}{c} L\rightarrow \infty \\ m=\rho L \end{array}}\frac{\alpha }{L}\frac{F_{0,L-2,m-1}(\lambda )}{ F_{1,L-1,m}(\lambda )}=\alpha \rho \lambda g_1=\frac{1-\sqrt{1-4\alpha \rho (1-\rho )}}{2}. \end{aligned}$$

(31)