Skip to main content
SpringerLink
Log in

Evidence theory based optimal scale selection for multi-scale ordered decision systems

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

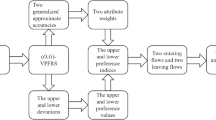
Abstract

In real data sets, objects are usually measured by multiple scales under the same attribute. Many information systems are given dominance relations on account of various factors which make classical equivalence relations change accordingly. This paper investigates the optimal scale selection for multi-scale ordered decision systems based on evidence theory. Five concepts of optimal scales related to rough set theory and the Dempster–Shafer theory of evidence in multi-scale ordered information/decision systems are first defined. Relationships are then clarified among \(\ge\)-optimal scale, \(\ge\)-lower approximation and \(\ge\)-upper approximation optimal scales as well as \(\ge\)-belief and \(\ge\)-plausibility optimal scales in multi-scale ordered information systems and consistent multi-scale ordered decision systems respectively. Finally, in inconsistent multi-scale ordered decision systems, by introducing a notion of \(\ge\)-generalized decision optimal scale, relationships among different types of optimal scales are also examined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bao H, Wu WZ, Zheng JW, Li TJ (2021) Entropy based optimal scale combination selection for generalized multi-scale information tables. Int J Mach Learn Cybern 12(5):1427–1437

    Article  Google Scholar 

  2. Chen DG, Li WL, Zhang X, Kwong S (2014) Evidence-theory-based numerical algorithms of attribute reduction with neighborhood-covering rough sets. Int J Approx Reason 55(3):908–923

    Article  MathSciNet  Google Scholar 

  3. Chen DG, Xu WH, Li JH, Hu QH (2020) Basic course of granular computing (in Chinese). Science Press, Beijing

    Google Scholar 

  4. Chen CLP, Zhang CY (2014) Data-intensive applications, challenges, techniques and technologies: a survey on big data. Inf Sci 275:314–347

    Article  Google Scholar 

  5. Dempster AP (1967) Upper and lower probabilities induced by a multivalued mapping. Ann Inst Stat Math 38(2):325–339

    Article  MathSciNet  Google Scholar 

  6. Du WS, Hu BQ (2016) Attribute reduction in ordered decision tables via evidence theory. Inf Sci 364–365:91–110

    Article  Google Scholar 

  7. Du WS, Hu BQ (2016) Dominance-based rough set approach to incomplete ordered information systems. Inf Sci 346–347:106–129

    Article  MathSciNet  Google Scholar 

  8. Greco S, Matarazzo B, Slowinski R (1999) Rough approximation of a preference relation by dominance relations. Eur J Oper Res 117(1):63–83

    Article  Google Scholar 

  9. Greco S, Matarazzo B, Slowinski R (2001) Rough sets theory for multicriteria decision analysis. Eur J Oper Res 129(1):1–47

    Article  Google Scholar 

  10. Greco S, Matarazzo B, Slowinski R (2002) Rough approximation by dominance relations. Int J Intell Syst 17(2):153–171

    Article  Google Scholar 

  11. Greco S, Matarazzo B, Slowinski R (2007) Dominance-based rough set approach as a proper way of handling graduality in rough set theory. Transactions on Rough Sets VII. Lect Notes Comput Sci 4400:36–52

    Article  Google Scholar 

  12. Gu SM, Wu Y, Wu WZ, Li TJ (2014) Knowledge approximations in multi-scale ordered information systems. In: Proceedings of International Conference on Rough Sets and Knowledge Technology, October 24-26, 2014, Shanghai, China. Lecture Notes in Computer Science, vol 8818. Springer, Berlin, pp 525–534

  13. Hu CX, Zhang L (2021) Dynamic dominance-based multigranulation rough sets approaches with evolving ordered data. Int J Mach Learn Cybern 12(1):17–38

    Article  Google Scholar 

  14. Huang B, Wu WZ, Yan JJ, Li HX, Zhou XZ (2020) Inclusion measure-based multi-granulation decision-theoretic rough sets in multi-scale intuitionistic fuzzy information tables. Inf Sci 507:421–448

    Article  Google Scholar 

  15. Huang QQ, Li TR, Huang YY, Yang X, Fujita H (2020) Dynamic dominance rough set approach for processing composite ordered data. Knowl Based Syst 187:104829

  16. Huang ZH, Li JJ, Dai WZ, Lin RD (2019) Generalized multi-scale decision tables with multi-scale decision attributes. Int J Approx Reason 115:194–208

    Article  MathSciNet  Google Scholar 

  17. Li F, Hu BQ (2017) A new approach of optimal scale selection to multi-scale decision tables. Inf Sci 381:193–208

    Article  Google Scholar 

  18. Li JH, Wang F, Wu WZ, Xu WH, Yang XB, She YH (2021) Review of multi-granularity data analysis methods based on granular computing (in Chinese). J Data Acquis Process 36(3):418–435

    Google Scholar 

  19. Li WK, Li JJ, Huang JX, Dai WZ, Zhang XP (2021) A new rough set model based on multi-scale covering. Int J Mach Learn Cybern 12(1):243–256

    Article  Google Scholar 

  20. Liang JY, Qian YH, Li DY, Hu QH (2015) Theory and method of granular computing for big data mining (in Chinese). Sci Sin Inf 45(11):1355–1369

    Article  Google Scholar 

  21. Lin TY, Yao YY, Zadeh LA (2002) Data mining, rough sets and granular computing. Physica-Verlag, Heidelberg

    Book  Google Scholar 

  22. Lingras PJ, Yao YY (1998) Data mining using extensions of the rough set model. J Am Soc Inf Sci 49(5):415–422

    Article  Google Scholar 

  23. Miao DQ, Li DY, Yao YY (2011) Uncertainty and granular computing (in Chinese). Science Press, Beijing

    Google Scholar 

  24. Pawlak Z (1991) Rough sets: theoretical aspects of reasoning about data. Kluwer Academic Publishers, Boston

    Book  Google Scholar 

  25. Pedrycz W, Skowron A, Kreinovich V (2008) Handbook of granular computing. Wiley, New York

    Book  Google Scholar 

  26. Shao MW, Zhang WX (2005) Dominance relation and rules in an incomplete ordered information system. Int J Intell Syst 20(1):13–27

    Article  Google Scholar 

  27. Shafer G (1976) A mathematical theory of evidence. Princeton University Press, Princeton

    Book  Google Scholar 

  28. Susmaga R (2014) Reducts and constructs in classic and dominance-based rough sets approach. Inf Sci 271:45–64

    Article  MathSciNet  Google Scholar 

  29. Wang HR, Li WT, Zhan T, Yuan KH, Hu XC (2021) Multi-granulation-based optimal scale selection in multi-scale information systems. Comput Electr Eng 92:107107

  30.  Wu WZ, Gu SM, Wang X (2015) Information granules in multi-scale ordered information systems. In: Proceeding of the 2015 International Conference on Machine Learning and Cybernetics, Guangzhou, China, July 12-15:182–187

  31. Wu WZ, Leung Y (2011) Theory and applications of granular labelled partitions in multi-scale decision tables. Inf Sci 181(18):3878–3897

    Article  Google Scholar 

  32. Wu WZ, Leung Y (2013) Optimal scale selection for multi-scale decision tables. Int J Approx Reason 54(8):1107–1129

    Article  MathSciNet  Google Scholar 

  33. Wu WZ, Leung Y, Zhang WX (2002) Connections between rough set theory and Dempster–Shafer theory of evidence. Int J Gen Syst 31(4):405–430

    Article  MathSciNet  Google Scholar 

  34. Xie JP, Yang MH, Li JH, Zheng Z (2018) Rule acquisition and optimal scale selection in multi-scale formal decision contexts and their applications to smart city. Future Gener Comput Syst 83:564–581

    Article  Google Scholar 

  35. Xu WH, Zhang XY, Zhong JM, Zhang WX (2010) Attribute reduction in ordered information systems based on evidence theory. Knowl Inf Sci 25(1):169–184

    Article  Google Scholar 

  36. Yao YY, Lingras PJ (1998) Interpretation of belief functions in the theory of rough sets. Inf Sci 104(1–2):81–106

    Article  MathSciNet  Google Scholar 

  37. Zhan JM, Zhang K, Wu WZ (2021) An investigation on Wu-Leung multi-scale information systems and multi-expert group decision-making. Expert Syst Appl 170:114542

  38. Zhang M, Xu LD, Zhang WX, Li HZ (2003) A rough set approach to knowledge reduction based on inclusion degree and evidence reasoning theory. Expert Syst  20(5):298–304

    Google Scholar 

  39. Zhang XQ, Zhang QH, Cheng YL, Wang GY (2020) Optimal scale selection by integrating uncertainty and cost-sensitive learning in multi-scale decision tables. Int J Mach Learn Cybern 11(5):1095–1114

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by grants from the National Natural Science Foundation of China (grant numbers 61976194, 41631179 and 62076221).

Author information

Authors and Affiliations

  1. School of Information Engineering, Zhejiang Ocean University, Zhoushan, 316022, Zhejiang, People’s Republic of China

    Jia-Wen Zheng, Wei-Zhi Wu, Han Bao & An-Hui Tan

  2. Key Laboratory of Oceanographic Big Data Mining and Application of Zhejiang Province, Zhejiang Ocean University, Zhoushan, 316022, Zhejiang, People’s Republic of China

    Jia-Wen Zheng, Wei-Zhi Wu, Han Bao & An-Hui Tan

Authors
  1. Jia-Wen Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wei-Zhi Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Han Bao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. An-Hui Tan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei-Zhi Wu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, JW., Wu, WZ., Bao, H. et al. Evidence theory based optimal scale selection for multi-scale ordered decision systems. Int. J. Mach. Learn. & Cyber. 13, 1115–1129 (2022). https://doi.org/10.1007/s13042-021-01438-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-021-01438-x

Keywords

Search

Navigation