Abstract
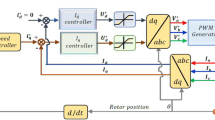
In this work, we propose the synthesis method of different robust fractional order PID controllers, which are synthesized from solving the constrained optimization algorithm for the permanent magnet synchronous motor (PMSM) speed control problem. This problem is formulated through the time and frequency-domain specifications where the obtained fractional controller should simultaneously satisfy some conflicted goals, such as good tracking dynamic behavior of the imposed set-point reference, good attenuation of the plant uncertainties, good suppression of the sensor noise effect and ensure an enough trade-off between the nominal performances and the robust stability of the feedback control system. The previous properties are satisfied not only for the nominal plant-model used in synthesis controller step, but also for a set of the neighboring plant uncertainties. Moreover, the integral time absolute error criterion should be minimized to satisfy the imposed time-domain requirements. However, the weighted-mixed sensitivity problem based upon the different proposed adjustable weights is minimized to ensure the imposed frequency-domain specifications where the load disturbances, sensor noises and the neglected nonlinear and fast PMSM dynamics are considered. The PMSM speed drive is controlled where its dynamic behavior is modeled by the unstructured-multiplicative uncertainty. The obtained simulation results are compared in time and frequency domains by those given with the conventional robust \(\mathcal {H}_\infty\) controller to demonstrate the effectiveness of the proposed fractional controllers.














Similar content being viewed by others
References
Freescale Semiconductor, Inc. (2016) Sensorless PMSM field oriented control. Design Reference Manual, Document Number: DRM148, Rev. 1 02/2016. http://www.nxp.com/doc/DRM148
Liu H, Li S (2012) Speed control for PMSM servo system using predictive functional control and extended state observer. IEEE Trans Ind Electron 59(2):1171–1183
Kim H, Son J, Lee J (2011) A high-speed sliding-mode observer for the sensorless speed control of a PMSM. IEEE Trans Ind Electron 58(9):4069–4077
Li S, Li Z (2009) Adaptive speed control for permanent-magnet synchronous motor system with variations of load inertia. IEEE Trans Ind Electron 56(8):3050–3059
Yadav AK, Gaur P, Saxena P (2016) Robust stability analysis of PMSM with parametric uncertainty using Kharitonov theorem. J Electr Syst 12(2):258–277
Zhou K (1995) Robust and optimal control. Prentice Hall, Upper Saddle River,
Zhou K (1999) Essentials of Robust control. Prentice Hall, Upper Saddle River
Doyle J, Francis B, Tannenbaum A (1990) Feedback control theory. Macmillan Publishing Co, New York
Francis BA (1987) A course in \(H_\infty\) control theory. In: Lecture notes in control and information sciences, vol 88. Springer, Berlin
Zhu M, Liu J, Lin Z, Meng H (2016) Mixed \({H}_2/{H}_\infty\) pitch control of wind turbine generator system based on global exact linearization and regional pole placement. Int J Mach Learn Cybern 7(5):921–930
Ball JA, Helton JW (1989) \({H}_\infty\) optimal control for nonlinear plants: connection with differential games. In: Proceedings of the 28th IEEE conference on decision and control, Tampa, FL, USA, 13–15 December 1989, pp 956–962. doi:10.1109/CDC.1989.70268
Ma Y, Jing Y (2015) Robust \({H}_\infty\) synchronization of chaotic systems with unmatched disturbance and time-delay. Int J Mach Learn Cybern. doi:10.1007/s13042-015-0468-9
Hua M, Tan H, Fei J, Ni J (2015) Robust stability and \({H}_\infty\) filter design for neutral stochastic neural networks with parameter uncertainties and time-varying delay. Int J Mach Learn Cybern 8(2):511–524
Safonov MG, Chiang RY (1989) A Schur method for balanced model reduction. IEEE Trans Autom Control 2:729–733
Safonov MG, Chiang RY, Limebeer DJN (1990) A Schur method for balanced model reduction. IEEE Trans Autom Control 35:496–502
Maruta I, Kim T-H, Sugie T (2009) Fixed-structure \({H}_\infty\) controller synthesis: a meta-heuristic approach using simple constrained particle swarm optimization. Automatica 4:553–559
Gumussoy S, Overton ML (2008) Fixed-order \({H}_\infty\) controller design via HIFOO, a specialized nonsmooth optimization package. 2008 American Control Conference Westin Seattle Hotel, Seattle, Washington, USA, June 11–13
Rajasekhar A, Abraham A, Pant M (2014) A hybrid differential artificial bee colony algorithm based tuning of fractional order controller for permanent magnet synchronous motor drive. Int J Mach Learn Cybern 5(3):327–337
Zang H, Qin Z, Dai Y (2014) Robust H-infinity space vector model of permanent magnet synchronous motor based on genetic algorithm. J Comput Inf Syst 10(14):5897–5905
Saptarshi D, Indranil P, Shantanu D et al (2012) Improved model reduction and tuning of fractional-order \(PI^\lambda D^\mu\) controllers for analytical rule extraction with genetic programming. ISA Trans 51:237–261
Podlubny I (1999) Fractional order systems and \({PI^\lambda D^\mu }\) controllers. IEEE Trans Autom Control 44:208–214
Oustaloup A, Levron F, Mathieu B (2000) Frequency-band complex non-integer differentiator: characterization and synthesis. IEEE Trans Circ Syst Fundam Theory Appl 47:25–39
Aidoud M, Sedraoui M, Lachouri A, Boualleg A (2016) A robustication of the two degree-of-freedom controller based upon multivariable generalized predictive control law and robust \({H}_\infty\) control for a doubly-fed induction generator. Trans Inst Meas Control. doi:10.1177/0142331216673425
Sedraoui M, Amieur T, Bachir Bouiadjra R, Sahnoun M (2015). A Robustified fractional-order controller based on adjustable fractional weights for a doubly fed induction generator. Trans Inst Meas Control (published online before print November 14, 2016, doi: 10.1177/0142331215617236)
Zhang BT, Pi Y (2012) Robust fractional order proportion-plus-differential controller based on fuzzy inference for permanent magnet synchronous motor. IET Control Theory Appl 6(6):829–837
Hwang C-L, Fang W-L, Shih C-L (2017) Globally neural-adaptive simultaneous position and torque variable structure tracking control for permanent magnet synchronous motors. J Vibr Control 14(1):147–163
Chang W, Tong S (2016) Adaptive fuzzy tracking control design for permanent magnet synchronous motors with output constraint. J Nonlinear Dyn. doi:10.1007/s11071-016-3043-3
Lundstrm P, Skogestad S, Wang ZQ (1991) Performance weight selection for \({H}\)-infinity and \(\mu\)-control methods. Trans Inst Meas Control 13:241–252
Oloomi H, Shafai B (2003) Weight selection in mixed sensitivity robust control for improving the sinusoidal tracking performance. In: 42nd IEEE conference on decision and control, vol 1, pp 300–305
Ortega MG, Rubio FR (2004) Systematic design of weighting matrices for the \(\cal{H}_\infty\) mixed sensitivity problem. J Process Control 14:89–98
Sarath SN (2011) Automatic weight selection algorithm for designing H-infinity controller for active magnetic bearing. Int J Eng Sci Technol 3:122–138
Mazandarani M, Kamyad AV (2013) Modified fractional Euler method for solving Fuzzy fractional initial value problem. Commun Nonlinear Sci Numer Simul 18:12–21
Mazandarani M, Najariyan M (2014) Type-2 fuzzy fractional derivatives. Commun Nonlinear Sci Numer Simul 19:2354–2372
Li X, Wang Y, Li N, Han M, Tang Y, Liu F (2016) Optimal fractional order PID controller design for automatic voltage regulator system based on reference model using particle swarm optimization. Int J Mach Learn Cybern. doi:10.1007/s13042-016-0530-2
Singiresu SR (2009) Engineering optimization: theory and practice, 4th edn. Wiley, Hoboken
Xu WJ (2012) Permanent magnet synchronous motor with linear quadratic speed controller. Energy Procedia 14:364–369
Acknowledgements
The authors would like to thank the referees and the editor for detailed comments that have helped significantly improve the quality of presentation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bachir Bouiadjra, R., Sedraoui, M. & Younsi, A. Robust fractional PID controller synthesis approach for the permanent magnetic synchronous motor. Int. J. Mach. Learn. & Cyber. 9, 2027–2041 (2018). https://doi.org/10.1007/s13042-017-0685-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-017-0685-5