Abstract
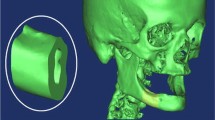
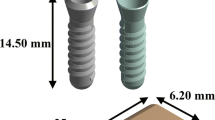
Several finite element models of bone-implant prosthetic derived with geometrical topology and material properties. Most of them adopted linear isotropic material properties to predict stresses around bone-implant interface. The objective of the present study is to compare stress distribution around bone-implant interface between two material models. In order to understand the biomechanical stress behavior at bone-implant interface, four different implant models were selected for the study. Mandibular bone section material models for isotropic and orthotropic material is defined with the contact between bone and implant surface to predict the von Mises stresses in the cancellous and cortical bone under the influence of vertical load of 100 N (coronal-apical), lateral load of 40 N (mesial-distal), and oblique load of 100 N at 45° to the axis of implant on crown surface. A nonlinear Abaqus CAE code is used to predict stresses distribution comparison between two material models.
The current study compares the result of stress in cancellous and cortical bone with isotropic and orthotropic material models. The stress distribution along the interface was presented for vertical, lateral, and oblique loading of selected implant models. Finite element (FE) numerical simulation result shows that the orthotropic material model is more acceptable than the isotropic material model to predict stress along bone-implant interface.










Similar content being viewed by others
Abbreviations
- D :
-
elastic stiffness parameter
- E :
-
elastic modulus, N/mm2
- G :
-
shear moduli, N/mm2
- μ :
-
Poisson’s ratio
- ϒ :
-
engineering material constant
References
Roy, S., Dey, S., Khutia, N., Chowdhury, A. R., & Datta, S. (2018). Design of patient specific dental implant using FE analysis and computational intelligence techniques. Applied Soft Computing, 65, 272–279.
Macedo, J. P., Pereira, J., Faria, J., Pereira, C. A., Alves, J. L., Henriques, B., Souza, J. C. M., & Lopez-Lopez, J. (2017). Finite element analysis of stress extent at peri-implant bone surrounding external hexagon or Morse taper implants. Journal of the Mechanical Behavior of Biomedical Materials, 71, 441–447.
Hasan, I., Röger, B., Heinemann, F., Keilig, L., & Bourauel, C. (2012). Influence of abutment design on the success of immediately loaded dental implants: experimental and numerical studies. Medical Engineering & Physics, 34, 817–825.
Cavallaro, J., & Greenstein, G. (2011). Angled implant abutments: a practical application of available knowledge. Journal of the American Dental Association (1939), 142, 150–158.
Okumura, N., Stegaroiu, R., Nishiyama, H., Kurokawa, K., Kitamura, E., Hayashi, T., et al. (2011). Finite element analysis of I plant-embedded maxilla model from CT data: comparison with the conventional model. Journal of Prosthodontic Research, 55, 24–31.
Tian, K., Chen, J., Han, L., Yang, J., Huang, W., & Wu, D. (2012). Angled abutments result in increased or decreased stress on surrounding bone of single-unit dental I plants: a finite element analysis. Medical Engineering & Physics, 34, 1526–1531.
Adell, R., Lekholm, U., Rockler, B., & Branemark, P. I. (1981). 15-Year.Study of osseointegrated implants in the treatment of the edentulous jaw. Journal of Oral Surgery, 10, 387–416.
Branemark, R., Branemark, P. I., Rydevik, B., & Myers, R. (2001). Osseointegration in skeletal reconstruction and rehabilitation. A review. Journal of Rehabilitation Research and Development, 38(2), 175–181.
Branemark, P. I., Breine, U., Adell, R., Hansson, O., Lindstom, J., & Ohlsson. (1969). Intra-osseous anchorage of dental prostheses. I. Experimental studies. Scandinavian Journal of Plastic and Reconstructive Surgery, 3, 81–100.
Branemark, P. I. (1983). Osseointegration and its experimental background. The Journal of Prosthetic Dentistry, 50(3), 399–410.
Schenk, R. K., & Buser, D. (1998). Osseointegration: a reality. Periodontology, 2000, 17, 22–35.
Vanegas-Acosta, J. C., Landinez P, N. S., Garzón-Alvarado, D. A., & Casale R, M. C. (2011). A finite element method approach for the mechanobiological modeling of the osseoinegration of a dental implant. Computer Methods and Programs in Biomedicine, 101, 297–314.
Taylor, D., Hazenberg, J. G., & Lee, T. C. (2007). Living with cracks: damage and repair in human bone. Nature Materials, 6(4), 263–268.
Gao, J., Xu, W., & Ding, Z. (2006). 3D finite element mesh generation of complicated tooth model based on CT slices. Computer Methods and Programs in Biomedicine, 82(2), 97–105.
Van Eijden, T. M. (2000). Biomechanics of the mandible. Critical Reviews in Oral Biology and Medicine, 11(1), 123–136.
Gačnik, F., Ren, Z., & Hren, N. I. (2014). Modified bone density-dependent orthotropic material model of human mandibular bone. Medical Engineering & Physics, 361, 684–1692.
Ding, X., Liao, S.-h., Zhu, X.-h., Wang, H.-m., & Zou, B.-j. (2015). Effect of orthotropic material on finite element modeling of completely dentate mandible. Materials and Design, 84, 144–153.
Wirtz, D. C., Pandorf, T., Portheine, F., Radermacher, K., Schiffers, N., Prescher, A., et al. (2003). Concept and development of an orthotropic FE model of the proximal femur. Journal of Biomechanics, 36(2), 289–293.
Peng, L., Bai, J., Zeng, X., & Zhou, Y. (2006). Comparison of isotropic and orthotropic material property assignments on femoral finite element models under two loading conditions. Medical Engineering & Physics, 28, 227–233.
Lengsfeld, M., Schmitt, J., Alter, P., Kaminsky, J., & Leppek, R. (1998). Comparison of geometry-based and CT voxel-based finite element modeling and experimental validation. Medical Engineering & Physics, 20(7), 515–522.
Kluess, D., Souffrant, R., Mittelmeier, W., Wree, A., Schmitz, K.-P., & Bader, R. (2009). A convenient approach for finite-element-analyses of orthopedic implants in bone contact: modeling and experimental validation. Computer Methods and Programs in Biomedicine, 95, 23–30.
Wirtz, D. C., Schiffers, N., Pandorf, T., Radermacher, K., Weichert, D., & Forst, R. (2000). Critical evaluation of known bone material properties to realize anisotropic FE-simulation of the proximal femur. Journal of Biomechanics, 33(10), 1325–1330.
Rho, J. Y., Hobatho, M. C., & Ashman, R. B. (1995). Relations of mechanical properties to density and CT numbers in human bone. Medical Engineering & Physics, 17(5), 347–355.
Taddei, F., Pancanti, A., & Viceconti, M. (2004). An improved method for the automatic mapping of computed tomography numbers onto finite element models. Medical Engineering & Physics, 26(1), 61–69.
Keyak, J. H., & Falkinstein, Y. (2003). Comparison of in situ and in vitro CT scan based finite element model predictions of proximal femoral fracture load. Medical Engineering & Physics, 25(9), 781–787.
Taylor, W. R., Roland, E., Ploeg, H., Hertig, D., Klabunde, R., Warner, M. D., et al. (2002). Determination of orthotropic bone elastic constants using FEA and modal analysis. Journal of Biomechanics, 35(6), 767–773.
Dhatrak, P., Shirsat, U., Sumanth, S., & Deshmukh, V. (2018). Finite element analysis and experimental investigations on stress distribution of dental implants around implant-bone interface. Materials Today: Proceedings, 55, 641–5648.
Dhatrak, P., Shirsat, U., Deshmukh, V., Sumanth, S. (2018) Fatigue life prediction of commercial dental implant using analytical approach and verification by FEA, Proceedings of Fatigue, Durability and Fracture Mechanics, Lecture Notes in Mechanical Engineering 203–212.
ABAQUS, Version 6.7 Documentation, ABAQUS Analysis Manual, Simulia, Dassault Systems, RI, USA 2007.
San Antonio, T., Ciaccia, M., Muller-karger, C., & Casanova, E. (2012). Orientation of Orthotropic material properties in a femur FE model: a method based on the principal stresses directions. Medical Engineering & Physis, 34, 914–919.
Jalali, S. K., Yarmohammadi, R., & Maghsoudi, F. (2016). Finite element stress analysis of functionally graded dental implant of a premolar tooth. Journal of Mechanical Science and Technology, 30(11), 4919–4923.
Zykova, Y., Kudryavtseva, V., Gai, M., Kozelskaya, A., Frueh, J., Sukhorukov, G., & Tverdohlebov, S. (2019). Free-standing microchamber arrays as a biodegradable drug depot system for implant coatings. European Polymer Journal, 114, 72–80. https://doi.org/10.1016/j.eurpolymj.2019.02.029.
Gai, M., Kurochkin, M. A., Li, D., Khlebtsov, B. N., Dong, L., Tarakina, N., Poston, R., Gould, D. J., Frueh, J., & Sukhorukov, G. B. (2018). In-situ NIR-laser mediated bioactive substance delivery to single cell for EGFP expression based on biocompatible microchamber-arrays. Journal of Controlled Release, 276, 84–92. https://doi.org/10.1016/j.jconrel.2018.02.044.
Gai, M., Frueh, J., Kudryavtseva, V. L., Yashchenok, A. M., & Sukhorukov, G. B. (2017). Polylactic acid sealed polyelectrolyte multilayer microchambers for entrapment of salts and small hydrophilic molecules precipitates. ACS Applied Materials & Interfaces, 9, 16536–16,545. https://doi.org/10.1021/acsami.7b03451.
Gai, M., Li, W., Frueh, J., & Sukhorukov, G. B. (2019). Polylactic acid sealed polyelectrolyte complex microcontainers for controlled encapsulation and NIR-laser based release of cargo. Colloids and Surfaces. B, Biointerfaces, 173, 521–528. https://doi.org/10.1016/j.colsurfb.2018.10.026.
Ipek Karacan, I., Macha, G., Choi, S., & Cazalbou, B. (2017). Ben-Nissan, antibiotic containing poly lactic acid/hydroxyapatite biocomposite coatings for dental implant applications. Key Engineering Materials, 758, 120–125. https://doi.org/10.4028//www.scientific.net//KEM.758.120.
Kim, S., Myung, W.-C., Lee, J.-S., Chai, J.-K., Jung, U.-W., Yang, H.-C., Lee, I.-S., & Choi, S.-H. (2011). The effect of fibronectin-coated implant on canine osseointegration. Journal of Periodontal Implant Science, 41, 242–247. https://doi.org/10.5051/jpis.2011.41.5.242.
Funding
This work is supported by Board of College and University Development (BCUD) Savitribai Phule Pune University, Pune, India, and M. A. Rangoonwala College of Dental Science and Research Centre, Pune, India.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
None
Research Involving Humans and Animals Statement
None.
Informed Consent
None.
Funding Statement
None.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Dhatrak, P., Girme, V., Shirsat, U. et al. Significance of Orthotropic Material Models to Predict Stress Around Bone-Implant Interface Using Numerical Simulation. BioNanoSci. 9, 652–659 (2019). https://doi.org/10.1007/s12668-019-00649-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12668-019-00649-5