1 Introduction

Equilibrium modeling for liberalized electricity markets and solving these models is of great practical relevance today. In this area, the main mathematical modeling tools are variational inequalities and complementarity problems. To obtain the latter, one usually first states the optimization problem of every player. In the convex case, which is typically considered in economics in general and in energy market modeling in particular, the optimal actions of the players can be characterized by their first-order optimality conditions. Together with suitably chosen market clearing conditions, the entire system is of the form of a mixed complementarity problem (MCP), which is often a linear one. For a general overview over linear complementarity problems (LCPs), we refer to the seminal textbook [15]. A detailed discussion about complementarity problems in energy markets is given in the book [22].

In the vast majority of papers on energy market modeling, the authors study a deterministic setting, i.e., all the data of the model is considered to be certain. However, many of the required parameters such as producers’ operating costs or the willingness to pay of consumers are not known in advance—especially in the case of long-run investment models that need to consider time or trading periods that are far in the future. Consequently, there is a strong need for uncertain electricity market equilibrium modeling. In mathematical optimization, there are mainly two approaches for tackling uncertain data: stochastic optimization (see, e.g., [8, 36]) and robust optimization (see, e.g., [2, 3, 53]). Both approaches have also been applied to the field of equilibrium modeling. However, the stochastic approach to LCPs is rather mature (see, e.g., [10,11,12, 44]) compared to the field of robust LCPs or robust market equilibrium problems, which are still in their infancies. The only studies we are aware of are [7, 40, 43, 54,55,56] on robust LCPs, [39, 45] on robust market equilibrium modeling, and the very recent and related paper [18] on robust bidding strategies in auctions. In this paper, we contribute to the second of the three mentioned fields and consider robustified market equilibrium models with transmission and generation investments.

In conventional power systems, generation and transmission investment (or expansion) planning has been performed in a centralized manner—typically using a cost minimization approach. However, in today’s restructured electricity markets both investment decisions as well as market outcomes are decentralized but need to be integrated to enable a proactive planning process. In proactive planning, a decision maker can anticipate the investment decisions of the other decision makers and the market outcome. This anticipative nature of decision making requires sequential, i.e., hierarchical, or simultaneous equilibrium models. There have been many developments in the applied electricity market literature regarding these models in recent years; please refer to, e.g., [48, 51] or the extensive reviews in [24] and [29] as well as the references therein.

One of the most prominent studies on simultaneous decision making for generation and transmission investment is presented in [57]. They have shown that co-optimizing generation and transmission investments results in lower investment costs compared to separately optimized investment decisions. This co-optimization model has been applied in US Eastern Interconnection and leads to cost-effective paths for investments. However, market outcomes are not investigated. On the other hand, there are several models that reflect the hierarchical nature as well as the market outcomes. The studies in [25, 31, 46] consider bilevel optimization problems in which transmission and generation investments are simultaneously considered in the bilevel problem’s upper level and the market is modeled in the lower level. Another stream of studies [34, 35, 49, 50] investigate hierarchical trilevel models that include transmission investments as the first level, generation investments as the second level, and the market outcomes are modeled as third-level decisions. Similar trilevel models are also considered in [1, 16, 26, 27, 38] where the first level models decisions of the regulator/operator such as market-design decisions or investment in transmission lines, the second level models generation investment as well as spot-market behavior of market participants, and the third level contains redispatch models as they are used in, e.g., Germany.

In many of these studies, bilevel or trilevel problems are cast as mathematical programs with equilibrium constraints (MPECs) or equilibrium problems with equilibrium constraints (EPECs) and are solved by equivalent single-level reformulations of the multilevel problem. In [9], the author shows that a hierarchical bilevel model formulated as an MPEC and a simultaneous model formulated as an MCP lead to the same results in a perfectly competitive market structure and under some mild conditions; see also, e.g., [13, 17] for similar results in comparable settings. Hence, in this paper, we resort our attention to MCP formulations.

Our contribution is the following. We study a robustification of a market equilibrium model for proactive investment planning in generation and transmission assets. By doing so, we explicitly consider long-run decisions based on market outcomes under uncertainty, which is of great importance in today’s restructured energy markets. We complement the literature on energy markets with stochastic uncertainties by handling the uncertainty in a robust way, which is especially important in risk-averse investment settings. Consequently, our models allow to shed light on the interdependencies between endogenously determined demand as well as generation in equilibrium models and long-run decision-making under uncertainty. Since classical strict robustness is often criticized for its very conservative solutions, we study the concept of \(\Gamma \)-robustness as it is proposed in [5, 6, 52] and as it is applied to market equilibrium models in [39] that we modify here to put emphasis on the relation between uncertainty and long-run decision-making. To the best of our knowledge, \(\Gamma \)-robustifications of investment models for generation and transmission expansion have not been considered before in the literature on energy market equilibrium models. To be more specific, we consider the willingness to pay of consumers as uncertain and allow a pre-specified number of \(\Gamma \) many consumers to deviate from their nominal willingness to pay in a worst-case way. We review a classical deterministic market equilibrium model in its MCP and variational inequality form in Sect. 2. There, we also state the equivalent welfare maximization problem. Afterward, in Sect. 3, we derive the \(\Gamma \)-robustified counterpart of the deterministic welfare maximization problem and show that it can also be obtained as an MCP based on a suitably robustified consumer problem. This shows that the robustified models are also economically meaningful. We then use the robustified models in Sect. 4 to analyze the effects of robustification on market outcomes as demand, generation, and prices as well as on investment decisions. Since we are interested in observing and understanding these main effects, we have used two case studies that allow us to clearly analyze the impact of robustification. Interestingly, our case studies reveal that the transmission system operator (who may invest in transmission line expansion) acts rather risk-neutral, whereas generating firms stop investing in new generation capacity already for mild uncertainties and thus act more risk-averse. The paper closes with some concluding remarks and open problems for future research in Sect. 6.

2 The deterministic model

2.1 General modeling assumptions and network setting

The deterministic equilibrium model discussed in this section is based on the electricity market equilibrium model given in [22], where the authors apply a well-simplified application of the study published in [30]. In the latter paper, an LCP for a Nash–Cournot market structure in bilateral or pool-type electricity markets is introduced; see [47] for a detailed version of this equilibrium model. Moreover, in [22] a stochastic version of the original equilibrium model is considered and solved with a generalized Benders decomposition approach. A robust version of this electricity market equilibrium model is presented in [39]. On the one hand, we simplify the economic setting by considering a perfectly competitive market but extend the model in [39] by incorporating generation and transmission investment decisions that affect the capacity of generators and transmission lines. Moreover, the specific setting of the robustification differs compared to the one studied in [39] since we do not bound the number of uncertainty realizations per consumer over time but bound the number of uncertainty realizations over the set of all consumers.

The basic assumptions of our generation and transmission investment planning model are as follows. We consider an equilibrium model for perfectly competitive day-ahead markets with transmission constraints. Balancing or real-time markets are not considered. As a common practice in the literature, transmission and generation investments will be done for a “target year” in the future; see, e.g., [14]. However, note that it can be extended to model a dynamic investment model for each year in the planning horizon; see, e.g., [37]. In compliance with the latter point, investment costs are discounted on an hourly basis. Potential generation investments are applicable for certain firms and buses, and they are bounded above. Similarly, transmission line investments are defined between certain buses and they are considered to have upper bounds as they are constrained by a certain available budget. Finally, for the ease of presentation, existing line capacity can be expanded without changing the line’s impedance in our market models. This simplifying assumption can be relaxed as in [49].

In our model, electricity generators can sell to all consumers in the entire system and they use the transmission system operator (TSO) as a mediator. In this structure, generating firms optimize their profits according to capacity and generation-sales constraints and the TSO optimizes its transmission service revenue according to the network constraints. The latter are modeled using lossless linear DC (direct current) load flow constraints. In addition, consumers change their amount of consumption as a reaction to price levels for optimizing their utility.

In this section, we first define each decision maker’s deterministic optimization problem separately and then form the overall equilibrium problem by concatenating each problem’s optimality conditions. Together with nodal flow balance equations, this leads to an MCP. The solutions of this MCP are market equilibria and the nodal electricity prices are, as usual, obtained as dual variables of the nodal balance equations; see, e.g., [14, 30]. Due to the fact that we consider a perfectly competitive market, all players act as price takers and we can thus state their optimization problems using exogenously given market prices.

In what follows, we model the electricity transmission network by using a connected and directed graph \(G = (I, A)\) with node (or bus) set I and arc set A. Transmission lines \(a \in A\) are usually denoted by its start and end points, e.g., \(a = (i,j)\) for start point \(i \in I\) and end point \(j \in I\). All notation used in the model is given in Table 1.

Table 1 Indices (top), variables (middle), and parameters (bottom) of the model
Full size table

2.2 Consumers

We start by introducing the models of the consumers that are located at the nodes \(i\in I\) of the network. The consumers decide on their demand \(d_i \ge 0\) and their willingness to pay is modeled by inverse market demand functions \(p_i = p_i(d_i)\). For the latter functions, we assume that they are continuous and strictly decreasing. Under this assumption, the gross consumer surplus

$$\begin{aligned} \int _0^{d_i} p_i(\omega ) \,\mathrm {d}\omega \end{aligned}$$

is a strictly concave function in \(d_i\) and the benefit maximization problem

$$\begin{aligned} \max _{d_i}&\quad \int _0^{d_i} p_i(\omega ) \,\mathrm {d}\omega -\pi _i d_i \end{aligned}$$
(1a)
$$\begin{aligned} \text {s.t.}&\quad d_i\ge 0 \end{aligned}$$
(1b)

of the consumer at node \(i\in I\) thus is a strictly concave maximization problem. Here and in what follows, \(\pi _i\) denotes the exogenously given market price at node \(i\in I\).

2.3 Generating firms

Every generating firm \(f \in F\) solves the problem

$$\begin{aligned} \max _{s_{f},x_{f},{\Delta K}_{f}} \quad&\sum _{i\in I} \pi _i s_{fi} - \sum _{i\in I_f} c_{fi}^\text {op}x_{fi} - \sum _{i\in I_f} c_{fi}^\text {inv}\Delta K_{fi} \end{aligned}$$
(2a)
$$\begin{aligned} \text {s.t.}\quad&\sum _{i\in I}s_{fi} - \sum _{i\in I_f} x_{fi} = 0,&[\nu _f] \end{aligned}$$
(2b)
$$\begin{aligned}&x_{fi}\le K_{fi} + \Delta K_{fi}, \quad i\in I_f,&[\mu _{fi}] \end{aligned}$$
(2c)
$$\begin{aligned}&\Delta K_{fi} \le \Delta K_{fi}^+, \quad i\in I_f,&[\delta _{fi}] \end{aligned}$$
(2d)
$$\begin{aligned}&x_{fi} \ge 0, \quad \Delta K_{fi} \ge 0, \quad i\in I_f, \end{aligned}$$
(2e)
$$\begin{aligned}&s_{fi}\ge 0,\quad i\in I, \end{aligned}$$
(2f)

where \(\Delta K_f = (\Delta K_{fi})_{i\in I_f}\) is the vector of all capacity investments of firm f, \(x_f = (x_{fi})_{i\in I_f}\) is the vector of all generations, and \(s_f = (s_{fi})_{i\in I}\) is the vector comprising all sales. The generating firm f is modeled as a price-taker, i.e., it assumes that the price at every single bus is exogenously given. The firms maximize their profits, which are given by revenue from sales less operating costs less discounted generation investment costs; see the objective function in (2a). Constraint (2b) models the balance of electricity generation and sales, capacity constraints are modeled in (2c), and upper bounds on the capacity investments are given in (2d). As it can be seen in (2c), generation investments affect the capacity constraints. Here and in what follows, dual variables are denoted by Greek letters and are given in parentheses next to the constraints. Finally, (2e) and (2f) ensure nonnegativity of generation, sales, and capacity investments. Since dual variables of simple nonnegativity constraints will be directly eliminated later, we do not state them here explicitly.

2.4 Transmission system operator

The model of the transmission system operator (TSO) is given by

$$\begin{aligned} \max _{\theta ,\Delta T} \quad&\sum _{(i,j)\in A} \left( \pi _j - \pi _i\right) B_{ij} \left( \theta _i-\theta _j\right) - \sum _{(i,j)\in A} c_{ij}^\text {exp}\Delta T_{ij} \end{aligned}$$
(3a)
$$\begin{aligned} \text {s.t.}\quad&B_{ij} \left( \theta _i-\theta _j \right) \le T_{ij} + \Delta T_{ij}, \quad (i,j) \in A,&[\lambda _{ij}^+] \end{aligned}$$
(3b)
$$\begin{aligned}&-B_{ij} \left( \theta _i-\theta _j\right) \le T_{ij} + \Delta T_{ij}, \quad (i,j) \in A,&[\lambda _{ij}^-] \end{aligned}$$
(3c)
$$\begin{aligned}&\Delta T_{ij} \le \Delta T_{ij}^+, \quad (i,j) \in A,&[\gamma _{ij}] \end{aligned}$$
(3d)
$$\begin{aligned}&-\pi \le \theta _i \le \pi , \quad i \in I\setminus \{i_0\},&[\varepsilon _i^-, \varepsilon _i^+] \end{aligned}$$
(3e)
$$\begin{aligned}&\theta _{i_0} = 0,&[\xi ] \end{aligned}$$
(3f)
$$\begin{aligned}&\Delta T_{ij} \ge 0, \quad (i,j) \in A, \end{aligned}$$
(3g)

where \(\theta = (\theta _i)_{i\in I}\) is the vector of all phase angles in the network and \(\Delta T= (\Delta T_{ij})_{(i,j)\in A}\) comprises all transmission line capacity investments. The objective of the TSO is to effectively distribute the transmission system services considering lossless DC network constraints and to optimize its revenues obtained due to these operations. The TSO’s revenue optimization in this manner, in fact, ensures that firms cannot use market power to obtain more transmission rights in the competitive market; see  [30]. In other words, the system operator works as an arbitrageur who benefits from price differences between nodes. Furthermore, in this model, the TSO also decides on transmission line capacity investments \(\Delta T_{ij}\) for all transmission lines \((i,j) \in A\). The objective function (3a) denotes the revenue of the TSO, calculated as the price differences multiplied by power flows less discounted transmission line expansion costs. Constraints (3b) and (3c) model lossless DC power flow. Upper bounds on the transmission line expansion are given in (3d) and (3e) represents lower and upper bounds on the phase angles \(\theta _i\), \(i \in I\).Footnote 1 The phase angle of the reference bus \(i_0\) is fixed in (3f) to ensure a unique physical solution and, finally, (3g) ensures nonnegativity of capacity investments.

2.5 Market clearing

As market clearing conditions we use the nodal flow balance equations

$$\begin{aligned} d_i - \sum _{f \in F} x_{fi} + \sum _{(i,j)\in A} B_{ij} \left( \theta _i - \theta _j\right) -\sum _{(j,i)\in A}B_{ji}\left( \theta _j-\theta _i\right) = 0, \quad i \in I. \end{aligned}$$
(4)

Note that demand \(d_i\) at node i is the sum of all firms’ sales to that node, i.e., \(d_i = \sum _{f \in F} s_{fi}\).

2.6 A mixed complementarity market equilibrium model

The market equilibrium model including generation and transmission investments is mainly taken from [9] and it is presented as the following MCP, which is obtained by concatenating the optimality conditions (that are both necessary and sufficient in our case) of all players and the market clearing conditions.Footnote 2

$$\begin{aligned} 0\le d_i \perp&\ \pi _i-p_i(d_i)\ge 0,&i\in I, \end{aligned}$$
(5a)
$$\begin{aligned} 0\le s_{fi} \perp&\ \nu _f-\pi _i \ge 0,&f \in F, \ i \in I, \end{aligned}$$
(5b)
$$\begin{aligned} 0\le x_{fi} \perp&\ c_{fi}^{\text {op}} - \nu _f + \mu _{fi} \ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(5c)
$$\begin{aligned} 0\le \Delta K_{fi} \perp&\ c_{fi}^{\text {inv}} - \mu _{fi} + \delta _{fi} \ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(5d)
$$\begin{aligned} \nu _f \text { free} \perp&\ \sum _{i \in I} s_{fi} - \sum _{i \in I_f} x_{fi} = 0,&f \in F, \end{aligned}$$
(5e)
$$\begin{aligned} 0\le \mu _{fi} \perp&\ K_{fi} + \Delta K_{fi}-x_{fi}\ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(5f)
$$\begin{aligned} 0\le \delta _{fi} \perp&\ \Delta K_{fi}^+ - \Delta K_{fi}\ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(5g)
$$\begin{aligned} 0\le \Delta T_{ij} \perp&\ c_{ij}^{\text {exp}} - \lambda _{ij}^- - \lambda _{ij}^+ + \gamma _{ij} \ge 0,&(i,j)\in A, \end{aligned}$$
(5h)
$$\begin{aligned} 0\le \lambda _{ij}^+ \perp&\ T_{ij} + \Delta T_{ij}-B_{ij} \left( \theta _i-\theta _j \right) \ge 0,&(i,j)\in A, \end{aligned}$$
(5i)
$$\begin{aligned} 0\le \lambda _{ij}^- \perp&\ T_{ij} + \Delta T_{ij}+B_{ij} \left( \theta _i-\theta _j\right) \ge 0,&(i,j)\in A, \end{aligned}$$
(5j)
$$\begin{aligned} 0\le \gamma _{ij} \perp&\ \Delta T_{ij}^+-\Delta T_{ij}\ge 0,&(i,j)\in A, \end{aligned}$$
(5k)
$$\begin{aligned} 0\le \varepsilon _i^{+} \perp&\ \pi -\theta _i \ge 0,&i \in I\setminus \{i_0\}, \end{aligned}$$
(5l)
$$\begin{aligned} 0\le \varepsilon _i^{-} \perp&\ \theta _i + \pi \ge 0,&i \in I\setminus \{i_0\}, \end{aligned}$$
(5m)
$$\begin{aligned} \theta _i \text { free} \perp&\ \sum _{(i,j)\in A} B_{ij} \left( \pi _j-\pi _i\right) -\sum _{(j,i)\in A} B_{ji} \left( \pi _i-\pi _j\right) \nonumber \\&\ +\sum _{(i,j)\in A} B_{ij} \left( \lambda _{ij}^- - \lambda _{ij}^+ \right) - \sum _{(j,i)\in A} B_{ji} \left( \lambda _{ji}^--\lambda _{ji}^+\right) \nonumber \\&\ - \varepsilon _i^{+} + \varepsilon _i^{-} = 0,&i \in I\setminus \{i_0\}, \end{aligned}$$
(5n)
$$\begin{aligned} \theta _{i_0} \text { free} \perp&\ \sum _{(i,j)\in A} B_{ij} \left( \pi _j-\pi _i\right) -\sum _{(j,i)\in A} B_{ji} \left( \pi _i-\pi _j\right) \nonumber \\&\ +\sum _{(i,j)\in A} B_{ij} \left( \lambda _{ij}^- - \lambda _{ij}^+ \right) - \sum _{(j,i)\in A} B_{ji} \left( \lambda _{ji}^--\lambda _{ji}^+\right) =0,&\end{aligned}$$
(5o)
$$\begin{aligned} \xi \text { free} \perp&\ \theta _{i_0} = 0,&\end{aligned}$$
(5p)
$$\begin{aligned} \pi _i \text { free} \perp&\ d_i - \sum _{f \in F} x_{fi} + \sum _{(i,j)\in A} B_{ij} \left( \theta _i - \theta _j\right) \nonumber \\&\ -\sum _{(j,i)\in A}B_{ji}\left( \theta _j-\theta _i\right) = 0,&i \in I. \end{aligned}$$
(5q)

Note that the market clearing conditions are equipped with the beforehand exogenously given market prices as dual variables. Thus, we obtain a system in the primal variables \(d, s, x, \Delta K, \theta , \Delta T\) and in the dual variables \(\nu , \mu , \delta , \lambda ^+, \lambda ^-, \gamma , \varepsilon ^{-}, \varepsilon ^{+}, \xi , \pi \). A solution of this system, by construction, corresponds to solutions of the separate optimization problems presented in Sects. 2.2–2.4 that also satisfy the market clearing conditions (4). Thus, a solution of (5) is a market equilibrium and \(\pi = (\pi _i)_{i \in I}\) is the vector of market clearing nodal prices.

2.7 An equivalent welfare maximization problem

It is well-known that the MCP (5), which models the wholesale electricity market under perfect competition, is equivalent to the welfare maximization problem (WMP)

$$\begin{aligned} \max _{z} \quad&\sum _{i\in I} \int _0^{d_i} p_i(\omega ) \,\mathrm {d}\omega - \sum _{f\in F} \left( \sum _{i\in I_f} c_{fi}^{\text {op}}x_{fi} + \sum _{i\in I_f} c_{fi}^{\text {inv}}\Delta K_{fi}\right) - \sum _{(i,j)\in A}c_{ij}^{\text {exp}}\Delta T_{ij} \end{aligned}$$
(6a)
$$\begin{aligned} \text {s.t.}\quad&\text {Consumers: } (1\mathrm{b}) \quad \text {for all } i \in I, \end{aligned}$$
(6b)
$$\begin{aligned}&\text {Generating firms: } (2\mathrm{b})\text {--}(2\mathrm{f}) \quad \text {for all } f \in F, \end{aligned}$$
(6c)
$$\begin{aligned}&\text {TSO: } (3\mathrm{b})\text {--}(3\mathrm{g}), \end{aligned}$$
(6d)
$$\begin{aligned}&\text {Market clearing: } (\mathrm{4}) \end{aligned}$$
(6e)

with variables \(z = (d^\top , s^\top , x^\top , \Delta K^\top , \theta ^\top , \Delta T^\top )^\top \) as before. The equivalence can be shown by comparing the first-order optimality conditions of Problem (6)—which are, again, necessary and sufficient—with the MCP (5) and by identifying the dual variables of the market clearing conditions in (6e) with the equilibrium prices \(\pi _i\), \(i\in I\), of the MCP.

2.8 An equivalent variational inequality

In this section, we also present an equivalent formulation of the MCP model given in Sect. 2.6 as a variational inequality (VI). In general, the latter is given as the following problem. Given a feasible set \(K \subseteq \mathbb {R}^n\) and a vector-valued mapping \(G : \mathbb {R}^n \rightarrow \mathbb {R}^n\), the variational inequality problem \(\text {VI}(G,K)\) is to find a vector \(z^* \in K\) that satisfies

$$\begin{aligned} G(z^*)^\top (z - z^*) \ge 0 \quad \text {for all } z \in K. \end{aligned}$$
(7)

One advantage of VI formulations (compared to MCPs) is that only primal variables appear in the formulation. In the context of the market equilibrium problem studied so far, the feasible set is given by the feasible sets of all players in the market equilibrium problem and the market clearing conditions, i.e.,

$$\begin{aligned} K = \{z:(6\mathrm{b})\text {--}(6\mathrm{e}) \text { are satisfied}\}. \end{aligned}$$
(8)

Note that this set is a convex polyhedron. The variable vector of the VI thus is given by z and the VI’s mapping G is defined as

$$\begin{aligned} G(v) = \begin{pmatrix} -(p_i(d_i))_{i \in I}\\ 0\\ (c_{fi}^\text {op})_{f \in F, i \in I_f}\\ (c_{fi}^\text {inv})_{f\in F, i\in I_f}\\ 0\\ (c_{ij}^\text {exp})_{(i,j)\in A} \end{pmatrix}, \end{aligned}$$

where 0 here stands for the zero vector in appropriate dimension.

We close this section with some brief comments on existence and uniqueness of market equilibria. Existence can be easily shown using the VI approach of this section. Since the function G is continuous and because a nonempty, convex, and compact set \({\tilde{K}} \subseteq K\) exists that contains all solutions of the \(\text {VI}(G,K)\), standard VI theory can be applied that ensures the existence of a solution. Since the VI is equivalent to the MCP (5) and to the welfare maximization problem (6), this also implies the existence of solutions for these two formulations. The situation is much more complicated when it comes to uniqueness of solutions. To the best of our knowledge, there is no result in the literature that can be applied directly to the setting studied in this paper. For a related long-run model without DC power flow constraints, uniqueness of market equilibria is shown in [28]. Moreover, uniqueness of the solution of a short-run model, again without DC power flow constraints is proven in [42] for the case of transport costs. However, the most related study is given in [41]. There, a short-run market equilibrium model is analyzed that also incorporates DC power flow constraints. It is shown that equilibria are, in general, not unique. Thus, we do not expect uniqueness of solutions for the setting considered in this paper.

3 A \(\Gamma \)-Robustified market model

We now turn to the discussion of possible uncertainties in the models of the last section. In principle, the techniques presented in the following can be applied to handle uncertainties of different data such as, e.g., the future willingness to pay of consumers, the future operating costs of generators, or the future investment costs for extending the capacity of a transmission line. Here, we focus on the former as a prototypical parameter for two reasons. First, this parameter is very important in equilibrium models since demand influences prices, which themselves influence generation and thus investment. Second, considering future demand parameters as uncertain is also of great importance for practice; see, e.g., [4, 32, 45]. In the following, we consider a \(\Gamma \)-robustification of the WMP (6). To this end, we additionally assume that each inverse market demand function \(p_i\) is linear and strictly decreasing, i.e., \(p_i(d_i) = a_i + b_i d_i\) with \(a_i \ge 0\) and \(b_i < 0\). Thus, the MCP (5) is a mixed linear complementarity problem (MLCP). In what follows, we consider uncertainty in the intercepts \(a_i\), \(i\in I\), of the demand functions and use box-uncertainty sets centered around the nominal values. Thus, for given nominal values \({\bar{a}}_i\), \(i\in I\), of the price-intercepts we have \(a_i = {\bar{a}}_i + u_i\) with

$$\begin{aligned}&u=(u_i)_{i\in I}\in {\mathcal {U}}\mathrel {{\mathop :}{=}}\{u\in \mathbb {R}^{|I|}:-\Delta a_i\le u_i\le \Delta a_i, \, \Delta a_i\ge 0, \, i\in I,\,\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad |\{i\in I:u_i\ne 0\}|\le \Gamma \}. \end{aligned}$$

Here, \(|I| \ge \Gamma \in \mathbb {N}\) is the number of uncertain price-intercepts that we hedge against in a worst-case sense. Next, we show that we obtain the same model if we either

  1. 1.

    robustify the welfare maximization problem (6) or

  2. 2.

    first robustify a properly chosen aggregated model of the consumers and then derive an MLCP as well as an equivalent optimization model.

In the described \(\Gamma \)-robust setting, the robust counterpart of (6) reads as

$$\begin{aligned} \max _{z} \quad&\sum _{i\in I} \int _0^{d_i} \left( {\bar{a}}_i+b_i\omega \right) \,\mathrm {d}\omega - \sum _{f\in F} \left( \sum _{i\in I_f} c_{fi}^{\text {op}}x_{fi} + \sum _{i\in I_f} c_{fi}^{\text {inv}}\Delta K_{fi}\right) \nonumber \\&\quad - \sum _{(i,j)\in A}c_{ij}^{\text {exp}}\Delta T_{ij} -\max _{\{J\subseteq I:|J|\le \Gamma \}}\left\{ \sum _{i\in J}\Delta a_i d_i\right\} \end{aligned}$$
(9a)
$$\begin{aligned} \text {s.t.}\quad&(6\mathrm{b})\text {--}(6\mathrm{e}). \end{aligned}$$
(9b)

Note that we only consider the price intercepts of the inverse market demand functions to be uncertain, whereas the slopes are considered to be certain. The reasons for this are twofold. First, this leads to a much more streamlined presentation of the results since we omit the technicalities required if slopes are also uncertain. Second, it is rather standard for electricity market equilibrium models including fluctuating demand of consumers that are modeled using inverse market demand functions that price intercepts change over time while the slopes are kept constant; see, e.g., [27, 28]. The same assumption is also made, e.g., in [21] for the case of uncertain demand. Regarding a study in which the slopes are considered to be uncertain as well we refer to [39].

Using the techniques as in, e.g., [39, 43], we obtain the following equivalent reformulation of the robust counterpart (9).

Theorem 3.1

The \(\Gamma \)-robust counterpart (9) of the welfare maximization problem (6) is equivalent to

$$\begin{aligned} \max _{z,\alpha ,\beta } \quad&\sum _{i\in I} \int _0^{d_i} \left( {\bar{a}}_i+b_i\omega \right) \,\mathrm {d}\omega - \sum _{f\in F} \left( \sum _{i\in I_f} c_{fi}^{\text {op}}x_{fi} + \sum _{i\in I_f} c_{fi}^{\text {inv}}\Delta K_{fi}\right) \nonumber \\&\quad - \sum _{(i,j)\in A}c_{ij}^{\text {exp}}\Delta T_{ij} -\sum _{i\in I}\beta _i -\alpha \Gamma \end{aligned}$$
(10a)
$$\begin{aligned} \text {s.t.}\quad&(6\mathrm{b})\text {--}(6\mathrm{e}), \end{aligned}$$
(10b)
$$\begin{aligned}&\beta _i +\alpha -\Delta a_i d_i\ge 0,\quad i\in I, \quad [\rho _i] \end{aligned}$$
(10c)
$$\begin{aligned}&\beta _i\ge 0, \quad i\in I, \end{aligned}$$
(10d)
$$\begin{aligned}&\alpha \ge 0, \end{aligned}$$
(10e)

where \(\beta =(\beta _i)_{i\in I}\).

In what follows, we abbreviate the robustified welfare maximization problem (10) by RWMP. As RWMP is a concave maximization problem over a polyhedral feasible set, its necessary and sufficient first-order optimality conditions can be stated as the MCP

$$\begin{aligned} 0\le d_i \perp&\ \pi _i+\Delta a_i\rho _i-\bar{a}_i-b_id_i\ge 0,&i\in I,\qquad \end{aligned}$$
(11a)
$$\begin{aligned} 0\le s_{fi} \perp&\ \nu _f-\pi _i \ge 0,&f \in F, \ i \in I, \end{aligned}$$
(11b)
$$\begin{aligned} 0\le x_{fi} \perp&\ c_{fi}^{\text {op}} - \nu _f + \mu _{fi} \ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(11c)
$$\begin{aligned} 0\le \Delta K_{fi} \perp&\ c_{fi}^{\text {inv}} - \mu _{fi} + \delta _{fi} \ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(11d)
$$\begin{aligned} \nu _f \text { free} \perp&\ \sum _{i \in I} s_{fi} - \sum _{i \in I_f} x_{fi} = 0,&f \in F, \end{aligned}$$
(11e)
$$\begin{aligned} 0\le \mu _{fi} \perp&\ K_{fi} + \Delta K_{fi}-x_{fi}\ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(11f)
$$\begin{aligned} 0\le \delta _{fi} \perp&\ \Delta K_{fi}^+ - \Delta K_{fi}\ge 0,&f \in F, \ i \in I_f, \end{aligned}$$
(11g)
$$\begin{aligned} 0\le \Delta T_{ij} \perp&\ c_{ij}^{\text {exp}} - \lambda _{ij}^- - \lambda _{ij}^+ + \gamma _{ij} \ge 0,&(i,j)\in A,\qquad \end{aligned}$$
(11h)
$$\begin{aligned} 0\le \lambda _{ij}^+ \perp&\ T_{ij} + \Delta T_{ij}-B_{ij} \left( \theta _i-\theta _j \right) \ge 0,&(i,j)\in A,\qquad \end{aligned}$$
(11i)
$$\begin{aligned} 0\le \lambda _{ij}^- \perp&\ T_{ij} + \Delta T_{ij}+B_{ij} \left( \theta _i-\theta _j\right) \ge 0,&(i,j)\in A,\qquad \end{aligned}$$
(11j)
$$\begin{aligned} 0\le \gamma _{ij} \perp&\ \Delta T_{ij}^+-\Delta T_{ij}\ge 0,&(i,j)\in A,\qquad \end{aligned}$$
(11k)
$$\begin{aligned} 0\le \varepsilon _i^{+} \perp&\ \pi -\theta _i \ge 0,&i \in I\setminus \{i_0\},\qquad \end{aligned}$$
(11l)
$$\begin{aligned} 0\le \varepsilon _i^{-} \perp&\ \theta _i + \pi \ge 0,&i \in I\setminus \{i_0\},\qquad \end{aligned}$$
(11m)
$$\begin{aligned} \theta _i \text { free} \perp&\sum _{(i,j)\in A} B_{ij} \left( \pi _j-\pi _i\right) -\sum _{(j,i)\in A} B_{ji} \left( \pi _i-\pi _j\right) \nonumber \\&+\sum _{(i,j)\in A} B_{ij} \left( \lambda _{ij}^- - \lambda _{ij}^+ \right) - \sum _{(j,i)\in A} B_{ji} \left( \lambda _{ji}^--\lambda _{ji}^+\right) \nonumber \\&- \varepsilon _i^{+} + \varepsilon _i^{-} = 0,&i \in I\setminus \{i_0\},\qquad \end{aligned}$$
(11n)
$$\begin{aligned} \theta _{i_0} \text { free} \perp&\sum _{(i,j)\in A} B_{ij} \left( \pi _j-\pi _i\right) -\sum _{(j,i)\in A} B_{ji} \left( \pi _i-\pi _j\right) \nonumber \\&+\sum _{(i,j)\in A} B_{ij} \left( \lambda _{ij}^- - \lambda _{ij}^+ \right) - \sum _{(j,i)\in A} B_{ji} \left( \lambda _{ji}^--\lambda _{ji}^+\right) =0,&\qquad \end{aligned}$$
(11o)
$$\begin{aligned} \xi \text { free} \perp&\ \theta _{i_0} = 0,&\qquad \end{aligned}$$
(11p)
$$\begin{aligned} \pi _i \text { free} \perp&\ d_i - \sum _{f \in F} x_{fi} + \sum _{(i,j)\in A} B_{ij} \left( \theta _i - \theta _j\right) \nonumber \\&\ -\sum _{(j,i)\in A}B_{ji}\left( \theta _j-\theta _i\right) = 0,&i \in I,\qquad \end{aligned}$$
(11q)
$$\begin{aligned} 0\le \alpha \perp&\Gamma -\sum _{i\in I}\rho _i\ge 0,&\qquad \end{aligned}$$
(11r)
$$\begin{aligned} 0\le \beta _i \perp&1-\rho _i\ge 0,&i\in I,\qquad \end{aligned}$$
(11s)

which we denote in the following by RMCP. This system is the same as (5) together with (11r) and (11s). Moreover, in (11a) we have the additional term \(\Delta a_i \rho _i\) compared to (5a).

Next, we robustify the aggregated consumer model, i.e., the model

$$\begin{aligned} \max _{d}\quad&\sum _{i\in I} \left( \int _0^{d_i} p_i(\omega ) \,\mathrm {d}\omega - \pi _i d_i \right) \end{aligned}$$
(12a)
$$\begin{aligned} \text {s.t.}\quad&d_i\ge 0,\quad i\in I. \end{aligned}$$
(12b)

Its robust counterpart is given by

$$\begin{aligned} \max _{d}\quad&\sum _{i\in I}\int _0^{d_i} \left( {\bar{a}}_i+b_i\omega \right) \,\mathrm {d}\omega -\sum _{i\in I}\pi _i d_i-\max _{\{J\subseteq I:|J|\le \Gamma \}}\left\{ \sum _{i\in J}\Delta a_i d_i\right\} \end{aligned}$$
(13a)
$$\begin{aligned} \text {s.t.}\quad&d_i\ge 0,\quad i\in I. \end{aligned}$$
(13b)

Again, using the techniques as in, e.g., [39, 43], we obtain the following reformulation of the robust counterpart (13).

Theorem 3.2

The \(\Gamma \)-robust counterpart (13) is equivalent to

$$\begin{aligned} \max _{d,\alpha ,\beta } \quad&\sum _{i\in I} \int _0^{d_i} \left( {\bar{a}}_i+b_i\omega \right) \,\mathrm {d}\omega - \sum _{i\in I} \pi _id_i -\alpha \Gamma -\sum _{i\in I}\beta _i \end{aligned}$$
(14a)
$$\begin{aligned} \text {s.t.}\quad&\beta _i+\alpha -\Delta a_id_i\ge 0,\quad i\in I, \end{aligned}$$
(14b)
$$\begin{aligned}&d_i\ge 0,\ \beta _i\ge 0, \quad i\in I, \end{aligned}$$
(14c)
$$\begin{aligned}&\alpha \ge 0. \end{aligned}$$
(14d)

Now, we put all first-order optimality conditions of the generating firms, TSO, robustified aggregated consumer (14), and the nodal flow balance equations together. We call the resulting system the robust market equilibrium problem (RMEP). This system is equivalent to (11) resp. (10). The equivalence can be shown by comparing the first-order optimality conditions (11) of (10) with the RMEP and by identifying the dual variables of the flow balance equations with the equilibrium prices \(\pi _i\), \(i\in I\), of the RMCP.

As we did for the MCP (5) in Sect. 2.8, we also present an equivalent formulation of the RMCP as a variational inequality. We use the same notation as in Sect. 2.8. The variable vector is given by \(v=(z^\top , \alpha , \beta ^\top )^\top \) and the feasible set reads

$$\begin{aligned} K=\{v:(10\mathrm{b})\text {--}(10\mathrm{e}) \text { are satisfied}\}. \end{aligned}$$
(15)

Finally, the VI’s mapping G is defined as

$$\begin{aligned} G(v) = \begin{pmatrix} -({\bar{a}}_i+b_id_i)_{i \in I}\\ 0\\ (c_{fi}^\text {op})_{f \in F, i \in I_f}\\ (c_{fi}^\text {inv})_{f\in F, i\in I_f}\\ 0\\ (c_{ij}^\text {exp})_{(i,j)\in A}\\ \Gamma \\ (1)_{i\in I} \end{pmatrix}. \end{aligned}$$

The existence of \(\Gamma \)-robustified solutions can be shown in analogy to the existence of nominal solutions as discussed at the end of Sect. 2.

Fig. 1
figure 1

3-Bus test system

Full size image

4 Case study #1: a 3-bus example

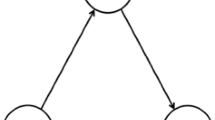
In this section, we apply the \(\Gamma \)-robust market equilibrium problem with transmission and generation investments derived in the last section to the academic 3-bus test system given in Fig. 1. This test case is taken and adapted from [30]. The situation is as follows. Firm 1 is located at bus 1 and firm 2 is located at bus 2. Both firms can invest in additional generation capacity. Demand, which is modeled using linearly decreasing inverse market demand functions is located at all three buses and all buses are connected with each other via existing transmission lines. The line connecting bus 1 and 2 has significantly less capacity and is the only transmission line for which the transmission capacity can be extended. All specific generation, demand, and line parameters are given in Table 2. Note that generation and transmission expansion cost parameters are discounted assuming a lifetime of 20 years and an interest rate of 3% per year. In this case study, we assume a representative hour that repeats itself during the year, i.e., 8760 times, and investment costs are discounted to a year.

Table 2 The parameters for the 3-bus system
Full size table

We implemented both the nominal and the robustified market equilibrium problem as a variational inequality in GAMS (version 24.6.1; see [23]) and solved them using PATH (version 4.7.04; see [20]) and the extended mathematical programming (EMP) framework [19] on a 2.3 GHz processor and 8 GB RAM. As this is a small-scale illustrative example, the solution times are less than a second for all considered models.

For getting some intuition for the equilibria in the deterministic setting, we first discuss the solutions of the nominal case in Sect. 4.1. Afterward, we discuss the numerical results for the \(\Gamma \)-robust market equilibria in Sect. 4.2.

4.1 The deterministic case

We start with discussing the numerical results for the nominal case and for four different scenarios that are characterized by the following two decisions.

Investment::

We consider the case in which both firms and the TSO are allowed to invest in generation and transmission capacity, respectively, and the case in which investment is not possible. The latter is obtained by setting \(\Delta K_{fi}^+ = 0\) and \(\Delta T_{ij}^+ = 0\).

Congestion::

We consider the case in which congestion can appear and the case in which transmission line capacities are considered to be sufficiently large. For the former case, we use the capacities given in Table 2.

Table 3 Numerical results for the market equilibrium model with and without investment as well as with and without congestion
Full size table

All results for all four possible scenarios are summarized in Table 3. First, without transmission line congestion, there is no investment (see the 4th and 5th column in Table 3)—even in the case in which it is allowed. As expected, without network congestion, net surplus is maximal (at an annual value of 77 047 000). The profit of firm 1 (which can produce cheaper than firm 2) in this case is the maximum and firm 2 (the more expensive one) makes no profit. Thus, the marginal operating cost of firm 2, i.e., 20  $/MWh, sets all nodal prices, which are equal since without congestion no price differences appear. Because an uncongested network does not lead to any investment incentives for the generating firms, generation and demand are strictly bounded above and, thus, consumer surplus (56 023 000) is small compared to the congested network cases.

If no investment is allowed in the case with congestion (3rd column), the profit of firm 1 is minimal. As it is the case also for firm 2, firm 1 produces at its capacity. Investment in generation capacity would be profitable (2 541 000 in column 3 vs. 7 200 000 in column 2) but is not possible. Moreover, the profit for firm 2 is maximal (134 000), which is the only setting in which firm 2 makes profit. This is due to the fact that firm 2 sells its entire generation (350 MW) from bus 2 to the TSO (at a price of 20.004, which is slightly higher than its operating costs of 20) and the TSO pays/gets a wheeling fee from firm 2 for transmitting power to buses 1 and 3. This wheeling fee is given by \(p_i(d_i) - p_3(d_3)\) (since we choose bus 3 to be the reference bus) and is negative (− 2.2) for bus 1, but positive for node 2 (2.2). The profit for firm 2 is \((p_2(d_2) - c_{22}^{\text {op}}) x_{22}\), because this formula omits wheeling fees the TSO gets/pays from/to firm 2 in order to transmit power to other nodes. This explanation is in line with the more detailed explanation given in, e.g., [30] and [47]. Thus, also the TSO’s revenues are maximal in this case since price differences are maximal. Indeed, the nodal prices are the lowest at bus 1 and 3 and highest at bus 2, where the price is the same for all scenarios.

Finally, when investments are allowed and there is congestion in the system, a better net surplus value is observed compared to the case without investments. This can be expected as new investment in transmission and generation capacity allows for higher net surplus. The profit of firm 1 is better off, whereas profit of firm 2 reduces completely to 0. Only in this case, a generation investment by firm 1 (55.8 MW) and a transmission expansion by the TSO (50 MW on line 1–2) can be observed. Thus (and as usual), scarce network capacities lead to investment incentives for generation. This, in turn, yields slightly higher nodal prices, except for bus 2. Since this case (2nd column) is for sure the most interesting one, it will be the base case for discussing the results of the robustified models in the next section.

4.2 The \(\Gamma \)-Robust case

In this section, we present and discuss the results for the \(\Gamma \)-robustified market equilibrium models. We consider uncertain demand, which is modeled via uncertain price-intercepts \(a_i, i = 1,2,3\), of the inverse market demand functions of the consumers. Since we have three consumers, we consider robustified equilibrium models for \(\Gamma \in \{0,1,2,3\}\), where \(\Gamma = 0\) corresponds to the nominal case and larger values of \(\Gamma \) lead to more conservative solutions. In particular, for \(\Gamma = 3\) we obtain the strictly robust counterpart so that the most conservative case is also covered. Moreover, we also vary the size of the uncertainty interval around the nominal price-intercept \({\bar{a}}_i\). Here, we consider intervals with 20–80% deviation around the nominal values. Again, larger possible deviations lead to more conservative solutions.

Fig. 2
figure 2

Top: nodal demands (\(d_i\) in MWh) vs.different uncertainty interval sizes. Bottom: nodal prices (\(\pi _i\) in $/MWh) vs.different uncertainty interval sizes. Both for \(\Gamma \in \{0,1,2,3\}\)

Full size image

4.2.1 Demands and prices

We start by discussing nodal demands and prices in the robustified market equilibria; see Fig. 2. The results show a clear pattern. With increasing uncertainty (i.e., larger \(\Gamma \) and/or larger uncertainty intervals), demands and prices are decreasing. This is in line with the results reported in [39] and can be explained as follows. The worst-case for the consumers corresponds to small surpluses, which are obtained if the price-intercept uncertainty reveals so that the consumer’s willingness to pay decreases. Since a decreased willingness to pay leads to less demand and thus smaller prices, this explains the trends visible in Fig. 2. One can also see that the prices converge to the operating cost of the cheapest producer in the network (firm 1 at bus 1). This, in particular, means that price differences converge to 0 in the network, i.e., uncertainty decreases regional differentiation between nodes that are visible in the nominal solution due to network constraints. Moreover, note that the demands decrease faster than price differences, which will be important for a later discussion.

Fig. 3
figure 3

Top: total generation by each firm (\(x_{fi}\) in MWh). Mid and bottom: Sales by firm 1 (mid; \(s_{1i}\) in MWh) and 2 (bottom; \(s_{2i}\) in MWh) at each node of the network. All vs.different uncertainty interval sizes and for \(\Gamma \in \{0,1,2,3\}\)

Full size image

4.2.2 Generation and sales

Figure 3 shows all generation and sales for all considered values of \(\Gamma \) and all considered uncertainty set sizes. The left-most figures (\(\Gamma = 0\)) show the results for the nominal equilibrium model. It can be seen in the top-most figure that generation is decreasing for larger uncertainty—which is clear since demands decrease as well. Moreover, both generators decrease their generation in almost the same way, leading to almost parallel curves. This also leads to the fact that firm 2 stops generation earlier than firm 1 simply because of its higher operating costs. Regarding sold quantities, we observe non-monotone behavior. We discuss the case of \(\Gamma = 2\) for the sales of firm 1 in detail, where we have an increase in sales of firm 1 to the consumer at bus 1 when we go from 40 to 60% of possible deviation from the nominal price-intercepts. This increase in uncertainty leads to less demand, which in turn excludes the more expensive firm 2 from the market; see \(\Gamma = 2\) in the top-most figure. Thus, the cheaper firm 1 needs to step in to satisfy the remaining demand. As a consequence, a larger uncertainty can—in special situations—also lead to an increase in sales for certain firms that remain in the market when others get too expensive to satisfy the reduced demand.

Fig. 4
figure 4

Surplus values (in $) vs.different uncertainty interval sizes and for \(\Gamma \in \{0,1,2,3\}\)

Full size image

Up to now, we observed that both demands and generations decrease if uncertainty increases. It is thus not surprising that consumer as well as total and net surpluses decrease as well—see Fig. 4, where it can be seen that all surplus measures converge to zero with larger uncertainty. We also observe that profit of firms almost immediately converge to zero in all uncertain cases. This means that almost all surplus is collected by the TSO.

Fig. 5
figure 5

Investments (in MW) vs.different uncertainty interval sizes and for \(\Gamma \in \{0,1,2,3\}\)

Full size image

4.2.3 Generation vs. transmission investment

As for the nominal case, we never observe investment in generation capacity of firm 2 so that Fig. 5 only shows investments in generation capacity by firm 1 and by the TSO in additional transmission capacity for line 1–2. For the nominal case (\(\Gamma = 0\)), we see that both firm 1 and the TSO are investing in additional capacity. However, for \(\Gamma \ge 1\), firm 1 stops investing directly, whereas the TSO still invests for \(\Gamma = 1\) (independent of the size of the uncertainty sets) and also still invests for \(\Gamma \in \{2,3\}\) for smaller uncertainty sets. It thus seems to be the case that generating firms act in a more risk-averse way, whereas the TSO behaves more risk-neutral. Putting it differently, the TSO pays the cost of uncertainty. The explanation is as follows: For this case study, it is obvious that the capacity of line 1–2 is very strict. Hence, in most scenarios it is better to invest in transmission capacity in order to maximize net surplus. Moreover, we already mentioned above that demands decrease faster than price differences if we increase the degree of uncertainty. Since total generation needs to decrease as total demand decreases, investment incentives for generating firms get weaker for larger uncertainty. On the other hand, we already observed that price differences stay larger also for larger uncertainties. Since the TSO mainly earns via price differences, cf. Problem (3), investment incentives for the TSO decrease more slowly than for generating firms when we increase \(\Gamma \) or the size of the uncertainty intervals.

5 Case study #2: a 30-bus example

In this section, a modified IEEE 30-bus system from [51] and [33] is used to demonstrate our approach for a larger case. In this case study, there are 6 generators (located at buses 1, 2, 13, 22, 23, and 27) and 39 lines. Different than the modified case study in [33], we do not consider new candidate lines, which would require binary variables for modeling expansion decisions. Another difference from both the studies in [51] and [33] is that we do not include quadratic cost parameters for generators in our model. Indeed, some preliminary numerical experiments revealed that the main conclusions are very similar with or without quadratic generation cost terms, which is why we choose to consider the simplified linear setting here for brevity. All firms can invest in generation capacity and all 39 existing lines are eligible for transmission expansion. The remaining generation, demand, and line parameters are presented in [51] and in Appendix 5.A of [33]. Similar to the case study in Sect. 4, we have solved both the nominal and the robustified market equilibrium problems as a variational inequality. All instances are again solved in less than one second of CPU time.

Table 4 Numerical results for the IEEE-30 bus system market equilibrium model with and without investment as well as with and without congestion
Full size table

5.1 The deterministic case

Similar to the scenarios in Table 3 of Sect. 4.1, the results for the nominal case are presented in Table 4. Without transmission line congestion, the results are identical for the cases with and without investments, which is why we list them as a single column (last column of Table 4). For the other cases, the table shows all generation investments by all firms and all transmission line investments by the TSO for the nominal case. It is visible that there is substantial generation and transmission investment in the case of network congestion. Hence, total and net surpluses are maximal, but the firms’ total profit (i.e., producer surplus) is minimal—only firm 2 enjoys extra profits when compared to the other cases.

The upper bound of generation for all firms is 60 MW and all firms except firm 1 are producing at this bound in the uncongested network cases and in the case with congestion but without investment (3rd and 4th column).

5.2 The \(\Gamma \)-robust case

In this section, we consider the \(\Gamma \)-robustified equilibrium model for \(\Gamma \in \{0,10,20,30\}\), where \(\Gamma = 0\) is equivalent to the nominal case and larger values lead to more conservative solutions. Note again that for \(\Gamma = 30\), we obtain the strictly robust case. As in Sect. 4.2, we vary the size of the uncertainty interval around the nominal price-intercept \({\bar{a}}_i\) between 20 and 80% of the nominal values.

We observe results regarding demand, prices, generation, and sales that are comparable to those for the 3-bus study. For instance, as uncertainty increases, consumer, total and net surpluses converge to zero; see Fig. 6, which shows qualitatively the same behavior as in Fig. 4 for the 3-bus study.

Fig. 6
figure 6

Surplus values (in $/hour) vs.different uncertainty interval sizes and for \(\Gamma \in \{0,10,20,30\}\)

Full size image
Fig. 7
figure 7

Generation investments by firms as percent of the generation investments in the nominal case under different uncertainty interval sizes and for \(\Gamma \in \{0,10,20,30\}\)

Full size image
Fig. 8
figure 8

Transmission investments by TSO at certain lines as percent of the transmission investments at certain lines in the nominal case under different uncertainty interval sizes and for \(\Gamma \in \{0,10,20,30\}\)

Full size image

In this case study, we have resorted our attention to the investment behavior of firms and the TSO, since these aspects also are the most interesting ones in the 3-bus case study. Figures 7 and 8 show the investments by firms in additional generation capacity as well as line investments by the TSO in the \(\Gamma \)-robustified settings for different levels of uncertainty. In both figures, the values are given as percentages w.r.t. the investments in the nominal case. It can again be seen that investments monotonically decrease if the level of uncertainty increases. Moreover, the investments of the TSO stay larger for increased levels of uncertainty when compared to the generation investments of the firms. This is similar to the observation for the 3-bus network in Sect. 4: Generating firms act in a more risk-averse way compared to the TSO who behaves more risk-neutral. This is also clearly supported by the level of expansion cost depicted in Fig. 9, where also the generation firms’ investment costs decline faster then the TSO’s investment costs.

Fig. 9
figure 9

Percent change in generation and transmission investment costs under different uncertainty interval sizes and for \(\Gamma \in \{0,10,20,30\}\)

Full size image

6 Conclusion

In this paper, we applied the concept of \(\Gamma \)-robustness to electricity market equilibrium models including investment opportunities in additional generation or transmission line capacity. To this end, we first introduced the nominal, i.e., certain, equilibrium problem as an MCP and also stated its variational inequality and welfare maximization counterpart. We then \(\Gamma \)-robustified the latter and showed that the resulting robustified welfare maximization problem is equivalent to a suitably chosen equilibrium model derived from suitably chosen and robustified consumer problems. This shows that the robustified market equilibrium problem is indeed economically meaningful. In two detailed case studies, we afterward presented numerical results for the robustified setting and then discussed the effects of robustification. In particular, in both case studies we observed a rather risk-neutral investment behavior for the TSO, whereas generating firms stop investments already for mild uncertainties and thus, act in a more risk-averse manner. Since this behavior can be observed for both considered networks and due to the explanations that we give for this behavior, we think that this qualitative difference between the investment of firms and the TSO is generalizable. However, we admit that the robustification of other uncertain parameters like production costs or technical network data might lead to different observations.

The area of robust market equilibria is a rather young field of research. Consequently, there are still many open research questions. Based on what we presented in this paper, we propose the following questions as interesting topics of future work:

  1. 1.

    How does robust equilibrium modeling interferes with market power modeling? It might be interesting to compare, both theoretically and computationally, how robust market equilibria depend on whether perfect competition models or models capturing market power are used.

  2. 2.

    Which other concepts of robust optimization can be carried over to market equilibrium modeling? It might, e.g., be interesting to see which effects can be observed when applying the concept of adjustable robustness to equilibrium models.

  3. 3.

    What policy conclusions can be drawn from applying robust equilibrium models to real-world electricity markets? Since, for sure, many parameters of electricity market models are uncertain (such as investment and operating costs of generating firms), such studies might be both of scientific as well as political interest.

Finally, let us close this paper with a rather general topic. The scientific community dealing with energy market equilibrium models is often discussing the question of what the “correct model” looks like. Should it be deterministic but with a high level of physical accuracy? Is a proper modeling of physics maybe less important but should there be a stronger emphasis on uncertainty modeling? If a stronger emphasis on uncertainty modeling is required, what kind of uncertainty model (stochastic or robust—risk-neutral or highly risk-averse) is the right one? These questions are long-lasting because they are hard to answer. Since in the recent past, more and more robust aspects entered the stage of energy market equilibrium modeling—and this paper hopefully serves as one contribution into this direction—a proper analysis now seems more achievable as before. For instance, equilibrium models including different ways of handling uncertainty can be fitted against real-world market outcomes to shed some light on the appropriateness of stochastic and robust equilibrium modeling.