Skip to main content
SpringerLink
Log in

Optimization techniques for the Brazilian natural gas network planning problem

  • Original Paper
  • Published:
Energy Systems Aims and scope Submit manuscript

Abstract

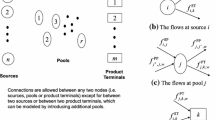
This work reports on modeling and numerical experience in solving the long-term design and operation planning problem of the Brazilian natural gas network. The considered planning problem involves a large amount of money to be invested in production, imports, shipping and delivery of natural gas for several uses in Brazil. In order to account for uncertainties related to the gas demand, mainly due to the use of gas for power production, we model the network planning problem by adopting a two-stage stochastic linear programming approach. We calculate the value of incorporating stochasticity into the problem and assess its numerical tractability in a real-life case by applying optimal scenario reduction techniques and a decomposition strategy based on bundle methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. http://www.aneel.gov.br/aplicacoes/capacidadebrasil/capacidadebrasil.cfm.

References

  1. Birge, J.R., Louveaux, F.V.: Introduction to Stochastic Programming. Springer Series in Operations Research Series. Springer, London (1997)

    MATH  Google Scholar 

  2. Bonnans, J., Gilbert, J., Lemaréchal, C., Sagastizábal, C.: Numerical Optimization: Theoretical and Practical Aspects, 2nd edn. Springer, New York (2006)

    MATH  Google Scholar 

  3. Correa, R., Lemaréchal, C.: Convergence of some algorithms for convex minimization. Math. Program. 62(2), 261–275 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  4. Dupacová, J., Gröwe-Kuska, N., Römisch, W.: Scenario reduction in stochastic programming: an approach using probability metrics. Math. Program. 95, 493–511 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  5. Fábián, C., Szőke, Z.: Solving two-stage stochastic programming problems with level decomposition. Comput. Manag. Sci. 4, 313–353 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Fábián, C.I.: Bundle-type methods for inexact data. In: Csendes T., Rapcsk T. (eds.) Proceedings of the XXIV Hungarian Operations Research Conference (Veszprém, 1999), vol. 8 (special issue), pp. 35–55 (2000)

  7. Heitsch, H., Römisch, W.: Scenario reduction algorithms in stochastic programming. Comput. Optim. Appl. 24, 187–206 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Heitsch, H., Römisch, W.: Scenario tree reduction for multistage stochastic programs. Comput. Manag. Sci. 6, 117–133 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Hellemo, L., Midthun, K., Tomasgard, A., Werner, A.: Multi-Stage Stochastic Programming for Natural Gas Infrastructure Design with a Production Perspective, chapter 10, pp. 259–288

  10. Hellemo, L., Midthun, K., Tomasgard, A., Werner, A.: Natural gas infrastructure design with an operational perspective. Energy Proc. 26(0), 67–73 (2012). 2nd Trondheim Gas Technology Conference

  11. Hiriart-Urruty, J.B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms. No. 305-306 in Grund. der math. Wiss. Springer (1993). (two volumes)

  12. Kazempour, S., Conejo, A.: Strategic generation investment under uncertainty via benders decomposition. IEEE Trans. Power Syst. 27(1), 424–432 (2012)

    Article  Google Scholar 

  13. Kelley Jr, J.: The cutting-plane method for solving convex programs. J. Soc. Ind. Appl. Math. 8(4), 703–712 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kleywegt, A.J., Shapiro, A., Homem-de Mello, T.: The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 12(2), 479–502 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  15. Li, X., Armagan, E., Tomasgard, A., Barton, P.I.: Long-term planning of natural gas production systems via a stochastic pooling problem. Am. Control Conf. (ACC) 2010, 429–435 (2010)

    Google Scholar 

  16. Li, X., Chen, Y., Barton, P.I.: Nonconvex generalized benders decomposition with piecewise convex relaxations for global optimization of integrated process design and operation problems. Ind. Eng. Chem. Res. 51(21), 7287–7299 (2012)

    Article  Google Scholar 

  17. Li, X., Tomasgard, A., Barton, P.: Nonconvex generalized benders decomposition for stochastic separable mixed-integer nonlinear programs. J. Optim. Theory Appl. 151, 425–454 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Maceira, M.E.P., Duarte, V.S., Penna, D.D.J., Moraes, L.A.M., Melo, A.C.G.: Ten years of application of stochastic dual dynamic programming in official and agent studies in Brazil: description of the NEWAVE program. Power Syst. Comput. Conf. 2008, 429–435 (2008)

    Google Scholar 

  19. Newham, N.: Power system investment planning using stochastic dual dynamic programming. Ph.D. thesis, University of Canterbury, New Zealand (2008). http://hdl.handle.net/10092/1975

  20. de Oliveira, W., Sagastizábal, C.: Level bundle methods for oracles with on-demand accuracy. Optim. Methods Softw. 29(6), 1180–1209 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. de Oliveira, W., Sagastizábal, C., Lemaréchal, C.: Convex proximal bundle methods in depth: a unified analysis for inexact oracles. Math. Program. 148, 241–277 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. de Oliveira, W.L., Sagastizábal, C., Penna, D.D.J., Maceira, M.E.P.N., Damázio, J.M.: Optimal scenario tree reduction for stochastic streamflows in power generation planning problems. Optim. Methods Softw. 25(6), 917–936 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. Pflug, G., Pichler, A.: A distance for multistage stochastic optimization models. SIAM J. Optim. 22(1), 1–23 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  24. Ruszczyński, A.: A regularized decomposition method for minimizing a sum of polyhedral functions. Math. Program. 35, 309–333 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  25. Sagastizábal, C.: Divide to conquer: decomposition methods for energy optimization. Math. Program. 134, 187–222 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  26. Santoso, T., Ahmed, S., Goetschalckx, M., Shapiro, A.: A stochastic programming approach for supply chain network design under uncertainty. Eur. J. Oper. Res. 167(1), 96–115 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  27. Schütz, P., Tomasgard, A., Ahmed, S.: Supply chain design under uncertainty using sample average approximation and dual decomposition. Eur. J. Oper. Res. 199(2), 409–419 (2009)

    Article  MATH  Google Scholar 

  28. Shapiro, A., Dentcheva, D., Ruszczyński, A.: Lectures on Stochastic Programming. Modeling and Theory, MPS-SIAM series on optimization, vol. 9. SIAM and MPS, Philadelphia (2009)

  29. Singh, K.J., Philpott, A.B., Wood, R.K.: Dantzig-Wolfe decomposition for solving multistage stochastic capacity-planning problems. Oper. Res. 57(5), 1271–1286 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. Slyke, R.V., Wets, R.B.: L-shaped linear programs with applications to optimal control and stochastic programming. SIAM J. Appl. Math. 17, 638–663 (1969)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

Research done during a postdoctoral visit of the third author at Instituto Nacional de Matemática Pura e Aplicada-IMPA. The authors are grateful to the reviewers for constructive suggestions that improved the original version of this article.

Author information

Authors and Affiliations

  1. PETROBRAS - Operations Research Department, Rio de Janeiro, 20020-100, Brazil

    Sergio V. B. Bruno & Leonardo A. M. Moraes

  2. UERJ - Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil

    Welington de Oliveira

Authors
  1. Sergio V. B. Bruno
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Leonardo A. M. Moraes
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Welington de Oliveira
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Welington de Oliveira.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bruno, S.V.B., Moraes, L.A.M. & de Oliveira, W. Optimization techniques for the Brazilian natural gas network planning problem. Energy Syst 8, 81–101 (2017). https://doi.org/10.1007/s12667-015-0172-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12667-015-0172-6

Keywords

Search

Navigation