Abstract
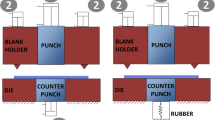
The present work addresses to evolving a sub-press equipment using rubber for counter force by which only two actions would be required to ensure fine piercing of 03 mm thickness, 25 mm diameter (shear area of 235 mm2) (a) Al, (b) EDD steel, (c) alpha brass and (d) 304 stainless steel sheet as opposed to five actions demanded with rigid tools (conventional-fine cutting). The errors with optimal conditions of impingement and rubber counter forces were compared with those reported in literature with rigid tools. The results obtained from the present work were quite promising. Errors were close to those achievable with rigid tools. For smooth shear of 95 % and above, the individual forces were registered and evaluated for a shear area of 235 mm2, so that, with this normalization, evaluation of individual forces for other material, thickness and perimeter could be enabled. Analogue parameters of the individual forces using that of commercially pure Al as the basis were then evaluated. These were evolved and furnished for both the ultimate tensile strength (Rm) as well as strength coefficient K of the flow equation of the form σF = K × εn. Such analogue parameters for Rm and K were compared and found to have a correlation factor of 0.93–0.99 reflecting the reliability of the present work. The techno-economics has thus been shown.











Similar content being viewed by others
References
Cutting, Bending and Deep Drawing (in German), Oëhler, Käiser, Springer (1962).
Cold Forming and Fine Blanking, BuderusEdelstahl Band GmbH, FeintoolTechnologie AG Lyss, Switzerland, Carl HanserVerlagMünchen Wien (2007).
Gopalakrishnan C K, and Venugopal P, Fine Piercing with Rubber as Counter Force in a Double Action Press, Paper no: S4089, Proceedings International Deep Drawing Research Group Conference-2012 [IDDRG, SMFRA (Sheet Metal Forming Research Association)] IIT Bombay, Nov 2012, p 639.
Metals Hand Book, Vol. 8 on Forming, ASM Publ, Columbus (1975).
Acknowledgments
Executive Vice President, Prof. R. Natarajan of M/S TI-Murugappa is gratefully acknowledged for supplying the annealed and Phosphated blanks of EDD steels towards this work free of cost.
Author information
Authors and Affiliations
Corresponding author
Appendix 1
Appendix 1
Guide line to use this diagram for any unknown geometry, thickness and material for determining the individual forces.
Since, literature [2, 4] provides data in terms of unit force per unit length of cut in fine cutting, the present work projects the force as force per shear area. These curves were generated by detailed experimentation for commercially pure aluminium, EDD steel alpha brass and 304 stainless steel to cover a range of strain hardening exponent of 0.08, 0.28, 0.388 and 0.56 respectively so that, the extension of this work for any unknown domestic or auto material can be inferred with this diagram. These forces were identified for hs1/S = 95 % and above smooth shear and 90 % of hs2/S and other errors within acceptable level.
1.1 How to Use the Previous Diagram for any Unknown Geometry, Thickness and Material for Determining the Individual Forces?
Current sheared area = (Π)(25)(3) = 235 mm2, Any piercing operation which is being done in unit can be taken. Let this chosen shear area be = S1 in mm2 (perimeter in mm) (thickness in mm).
\Then the individual forces can be calculated with the diagram in Fig. 12 as follows (for any material): Let us say that, S1 = 470 mm2 Let the material be EDD steel whose Rm is close to 300 MPa (Point a). Draw a vertical from close to 300 MPa to meet the total force line (Point b). Draw horizontal from this cutting point of b. The value of total force will then be known for shear of 235 mm2(Point c).
Let us say in this example, 150 is obtained as total force. Multiply this identified force component by (470/235) = 2 to obtain the material of your selection cited above. Then for shear area of 470, it will be 300 kN. Similar procedure can be followed to identify the other forces. For any unknown material whose Rm is known, the values can be inferred with this diagram. It should also be possible to infer the values of forces for various perimeters and thickness of materials also.
Figure 9a, b can also be used (with the analogue parameters), to check (for reliability) the individual forces for materials ranging from strain hardening exponent of 0.08 to 0.56 (if necessary, extrapolation or interpolation may also be used). The correlation factors are in the range of 0.93–0.99, the values so checked will be quite reliable.
This diagram is useful for calculating the semi-piercing forces as well (where in, the total and cutting forces will only be half that of complete piercing, while other forces such as impingement and counter forces will be the same.)
Rights and permissions
About this article
Cite this article
Aravind, U., Gopalakrishnan, C.K., Chakkingal, U. et al. Fine Piercing with Rubber for Counter Force in a Double Action Hydraulic Press. Trans Indian Inst Met 68 (Suppl 2), 235–242 (2015). https://doi.org/10.1007/s12666-015-0577-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12666-015-0577-x