Introduction

Apart from being a rock-forming mineral in carbonate rocks, calcite occurs also as a cement phase in sandstones (Bjørlykke et al. 1989). Many reservoir rocks consist of carbonate-cemented siliciclastic sediments including, for example, the Triassic Edvard Grieg sandstone in the Norwegian Sea (Markussen et al. 2019), and the Devonian Old Red Sandstone in the United Kingdom (Hillier et al. 2006). Knowing the rate of calcite cement dissolution under different environmental conditions is extremely important for predicting the temporal evolution of the mineral composition and the reservoir quality, and for estimating the reservoir exploitation capacity, since acid injection (matrix acidizing) is commonly used to stimulate production wells (McLeod 1984; Shafiq et al. 2019; Younesian-Farid and Sadeghnejad 2020). After their active service life, depleted carbonate-cemented reservoirs have the potential to serve as storage for energy and environmentally important substances, such as hydrogen (e.g., Henkel et al. 2014) and carbon dioxide (e.g., Bachu and Adams 2003), which also requires to account for potential fluid–rock interactions.

Due to their heterogeneous mineral composition and texture, carbonate-cemented sandstones are complex systems. It is unclear whether it is possible to transfer the existing knowledge acquired by mono-mineral studies on carbonates (e.g., Luquot and Gouze 2009; Molins et al. 2014; Rötting et al. 2015; Gray et al. 2018; Kahl et al. 2020) to the understanding of multi-mineral systems with complex fluid-flow pathways, where calcite occurs within an assemblage of different minerals (e.g., silicates, feldspars, and clays). With this question in mind, we investigated the dissolution kinetics of calcite at different time and length scales using a well-studied reservoir-type sandstone of the Upper Rotliegend from northern Germany (e.g., Fischer et al. 2007, 2012b; Henkel et al. 2014; Pedrosa et al. 2019, 2021; Heidsiek et al. 2020; Jacob et al. 2021; Monsees et al. 2021).

Although calcite reaction kinetics has received great attention in science for several decades (e.g., Plummer et al. 1978; Sjöberg and Rickard 1984; Chou et al. 1989; Morse and Arvidson 2002), the upscaling of experimental rates remains challenging (Meile and Tuncay 2006; Noiriel et al. 2020; Noiriel and Soulaine 2021). Modern methods for quantifying dissolution rates (e.g., atomic force microscopy and vertical scanning interferometry) can directly provide reliable reaction rates with a high spatial and temporal resolution (e.g., Vinson and Lüttge 2005; Bollermann and Fischer 2020; Kahl et al. 2020). When transferring these micro-scale rates to larger scales, however, discrepancies or scale effects are likely to occur (e.g., Li et al. 2006; Bouissonnié et al. 2018). In core samples, the shape and connectivity of the pore space (and its heterogeneity) determines the flow and transport properties, which additionally influence or limit both local and bulk averaged dissolution rates (e.g., Flukiger and Bernard 2009; Li et al. 2008; Molins et al. 2014; Al-Khulaifi et al. 2017). A heterogeneous distribution of the reacting mineral phase (i.e., mineralogical heterogeneity) creates additional complexity in the system. For example, pore-scale network models from Li et al. (2007) indicated that a varying size and orientation of the reactive mineral clusters lead to differences in dissolution rates at the mm-scale. By performing column experiments on magnesite–quartz mixtures, Salehikhoo et al. (2013) found rate deviations of up to 14% due to different spatial distributions of the reacting mineral phase.

For the tight sandstone under investigation, most of the calcite cement dissolution is expected to occur in the proportion of the mineral surface that is in direct contact with the major fluid-flow paths. Predicting this proportion is a practical problem, since the accessibility of a mineral phase in a rock is not directly quantifiable solely based on its volume fraction (Peters 2009; Landrot et al. 2012; Waldmann et al. 2014; Beckingham et al. 2016). The problem of fluid-accessible surface area is directly related to the difficulty in quantifying the reactive surface area (RSA) of a mineral or rock, which represents a key parameter in reactive transport modeling and is required to normalize chemical reaction rates (Fischer et al. 2014). Given the impossibility of a direct measurement method of the RSA (Lüttge and Arvidson 2008), parameters such as the specific surface area (SSA) or the geometric surface area (GSA) are used to calculate “surface normalized” reaction rates (e.g., Hodson 2006). Measuring the SSA by gas adsorption (BET) is the preferred analytical tool, but it does not allow to determine the surface area of separate mineral phases in consolidated rock. Thus, only an optical determination of a geometric calcite cement surface is appropriate for the studied sandstone. As a non-destructive method, X-ray micro-computed tomography (µXCT) is primarily used for characterizing the structure of mineral or rock samples and the geometry of the solid–pore interface in recent studies (Noiriel et al. 2005, 2009, 2019, 2020; Lai et al. 2015; Hinz et al. 2019; Svensson et al. 2019). If a sufficiently high spatial resolution or mineral surface retreat is reached, the evolution of fluid–solid interfaces can be observed and local reaction rates can be resolved (Noiriel and Soulaine 2021).

The objective of this study was to analyze, to compare, and to link the reaction rates of the calcite cement within a low-permeable (i.e., tight) reservoir sandstone under acidic conditions (pH 4.0) on the mineral surface and core scales: (1) flow-through experiments at the mineral surface were made using polished unreacted sandstone samples from a sample block. Vertical scanning interferometry (VSI) provided quantitative dissolution rates and microstructural information at the grain scale (µm to mm); (2) flow-through dissolution experiments on core samples (cm-scale) from the same sample block were conducted to investigate the long-term dissolution behavior. Inductively coupled plasma mass spectrometry (ICP-MS) was used to measure the calcium content of the effluent fluid and µXCT was used to parametrize the geometric surface area of the calcite cement for calculating core dissolution rates.

Based on this experimental study, we quantify the difference in calcite dissolution rates between the mineral surface and the core scale with significantly different transport conditions. In contrast to the far-from-equilibrium conditions at the mineral surface scale, more natural transport conditions were simulated at the core scale using low flow velocities, high chemical gradients, and near-equilibrium fluid conditions. Using µXCT imaging, we also aim to investigate the variability in geometry and fluid accessibility of the cement phase in the sandstone, which controls the reaction-available surface area and the effective dissolution rates. Finally, the µXCT-derived geometric calcite cement surface area connected to the open pore space is used to link the measured mineral surface rates to the measured core rates.

Materials and methods

Sample material

Samples of a natural reservoir-type sandstone from the Bebertal outcrop (Sachsen-Anhalt, Germany) were used in all experiments. The outcrop belongs to the Parchim formation (Havel sub-group, Upper Rotliegend) of the South Permian Basin (Kleditzsch and Kurze 1993; Plein 1993), with the facies investigated having similar deposition conditions and age as the reservoir rocks of the North German Basin (Fischer et al. 2012b). The sample material for the experiments was drilled from a sandstone block originating from the “Schwentesius” quarry, which was also used in earlier studies (Pedrosa et al. 2019, 2021; Heidsiek et al. 2020; Jacob et al. 2021).

The mineralogical composition of the sandstone sample block (Fig. 1a) was investigated by X-ray diffraction analysis and Rietveld analysis by Jacob et al. (2021). Calcite is mainly present as poikilitic eodiagenetic and mesodiagenetic cement (Fig. 1b, Heidsiek et al., 2020). Under the experimental conditions used (Sect. 2.2), calcite is the least stable and therefore considered the most reactive mineral phase in the sandstone. Four samples were drilled from the sandstone block for the core scale percolation experiments (Fig. 1a, C14, E6, F11, and G12), and one for the mineral surface dissolution experiments on the µm- to mm-scale (Fig. 1a, E7). The cylindrical samples had a diameter of 2.54 cm (1 inch), and were shortened to the required length of 5 cm or 1.5 cm for core experiments, and 5 mm for mineral surface experiments. The initial sample permeability ranged between 1.1 and 3.1 mD.

Fig. 1
figure 1

a Sampled sandstone block from the Upper Rotliegend formation (Bebertal, Germany). All samples for the dissolution experiments were drilled in the laminated and cross-bedded aeolian facies (unmasked area). b SEM image of the Rotliegend sandstone with partially porous calcite cement (light gray)

Full size image

Dissolution experiments

To determine dissolution rates of the calcite cement in the sandstone, dissolution experiments were performed using three types of flow-through setups: (1) an in-house built cell for mineral surface dissolution experiments (“micro-cell”); (2) an in-house built triaxial permeability cell; (3) an ICARE4 flow-through autoclave (Fig. 2). All experiments were carried out at room temperature using an infiltration solution containing 1 × 10–4 mol L−1 HCl and 1 × 10–3 mol L−1 NaCl prepared with ultra-pure water (resistivity > 18.2 MΩcm). At the core scale, two different experimental apparatuses were used to implement varying conditions in terms of differential pressure and hydraulic residence time. Table 1 includes the main similarities and differences of all three experimental setups.

Fig. 2
figure 2

Overview of the three experimental setups (schematically simplified): a micro-cell on the mineral surface scale, b triaxial permeability cells and c flow-through autoclave on the core scale

Full size image
Table 1 Experimental details of the dissolution experiments on the calcite cemented sandstone
Full size table

Micro-cell

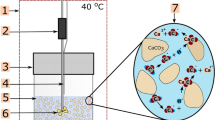
Mineral surface dissolution experiments were performed using an in-house designed flow-through cell (Fig. 2a, University of Bremen, e.g., Pedrosa et al. 2019, 2021; Li et al. 2021). The fluid chamber of the cell has an elongated shape with only 500 µm height, allowing for a relatively wide coverage of the sandstone sample while providing a small hydraulic residence time (HRT) (photo in Supplementary Information, Fig. SI1). The flow rate was set to 1.2 mL min−1, which results in an HRT of 3.8 s. Hence, the bulk fluid inside the cell was at all times fully undersaturated with respect to any mineral phase in the sandstone. The sample was reacted for a total of 120 min using the infiltration solution specified in Sect. 2.2. Thus, reaction time was much lower compared to the core experiments. Every 30 min, the sample was taken out of the fluid cell and its topography was measured using VSI.

Triaxial permeability cell

Flow-through experiments with a triaxial permeability cell were performed to investigate calcite cement dissolution in the core plugs under low differential pressures of < 0.5 bar (details in Supplementary Information, Fig. SI11). Initial sample saturation of the sandstone sample was achieved using a vacuum pump and an equilibrium solution (infiltration solution without acid). The pressure at the inlet of the cell (\({P}_{\mathrm{in}}\)) was controlled by the hydrostatic pressure of the infiltration solution and was regulated using compressed air. To inhibit sample bypass, a radial confining pressure (~ 2 × \({P}_{\mathrm{in}}\)) was applied by pressurized ultra-pure water in the chamber of the cell (Fig. 2b). Initially, the differential pressure was set to 0.2–0.3 bar and was afterward continuously monitored by digital manometers.

The outgoing fluid was sampled under atmospheric pressure using microtubes. After a minimum sample volume of 2.5 mL had been reached, the microtube was exchanged. The volumetric fluid-flow rate \(Q\) was quantified by measuring the sampled fluid volume \({V}_{\mathrm{fluid}}\) and sampling time \(\Delta t\)

$$Q=\frac{{V}_{\mathrm{fluid}}}{\Delta t}.$$
(1)

The pH of the solution at the sample outlet was measured with a WTW SenTix Mic pH electrode immediately after retrieving each fluid sample. The ionic concentration of calcium in the outlet fluid was measured using ICP-MS in an X-Series 2, Thermo Fisher Scientific.

Flow-through autoclave

A flow-through autoclave ICARE4 (designed at the Geosciences Department, University of Montpellier, France) was used for reacting the core plugs under elevated differential pressures of up to 20 bar (Fig. 2c). The ICARE4 (details in Supplementary Information, Fig. SI12) and similar devices have been previously used for reactive percolation experiments, such as for studying CO2–brine–rock interactions in context with carbon capture and storage (e.g., Myrttinen et al. 2012).

Radial sample confinement is controlled by an integrated pressure multiplier with a free-moving piston to prevent fluid bypass. The confining pressure was fixed to ~ 1.1 × \({P}_{\mathrm{in}}\). The experimental setup also comprises two motorized piston pumps to produce the flowrate and two back-pressure pumps to maintain a constant pressure at the outlet of the percolation cell (Table 1). The volumetric fluid-flow rate was adjusted according to the observed differential pressure ranging between 12 and 20 bar. Before starting the percolation, a complete saturation of the rock sample was achieved by an integrated vacuum pump. Sampling ports before and after the percolation cell enable fluid sample extraction with a fixed volume of 2.5 mL without a significant decrease in system pressure. For the subsequent chemical fluid analysis, the methodology described in Sect. 2.2.2 was applied.

Analytical methods

Direct calcite dissolution rates on mineral surface scale

For the calculation of the dissolution rates at the mineral surface, a ZeMapper white light interferometer (Zemetrics, Tucson, AZ, USA) was used to collect topography data using Mirau objectives with 20 × and 50 × magnification. Pixel sizes were 0.37 µm (20 ×) and 0.15 µm (50 ×), respectively, and the achieved height resolution (Z direction) is in the Ångström range (Arvidson and Morse 2014). This provides a measure for the surface height retreat by subtracting the sample’s height between each reaction interval (see Supplementary Information, Fig. SI2 for a 3D visualization example of the topography maps). Surface normalized calcite dissolution rates can be determined directly by

$$r_{Cc} = \frac{\Delta h}{{\Delta t \cdot V_{m} }}$$
(2)

where \(\Delta h\) is the height difference of the mineral surface between two consecutive topography measurements, \(\Delta t\) the reaction time interval (30 min), and \({V}_{m}\) the molar volume of calcite (3.693 × 10–5 m3 mol−1). Six locations (calcite cement patches) and 12 areas of interest were selected from the reacted areas for a statistical rate analysis as described in Pedrosa et al. (2019).

Indirect calcite dissolution rates on core scale

Total calcite dissolution rates for the core plugs (in units mol s−1) were calculated for different reaction times using the ionic calcium concentration obtained from ICP-MS analysis (\({C}_{Ca}\)) and the volumetric flow rate \(Q\)

$$r_{{Cc,{\text{total}}}} = C_{Ca} \cdot Q.$$
(3)

Surface normalized calcite dissolution rates (in units mol m−2 s−1) were needed for the comparison with the rates obtained at the mineral surface scale and were calculated using

$$r_{Cc} = \frac{{r_{{Cc,{\text{total}}}} }}{A} = \frac{{r_{{Cc,{\text{total}}}} }}{{GSA_{{Cc,{\text{open}}}} }}.$$
(4)

In this study, a geometric surface area (\({GSA}_{Cc,\mathrm{open}}\)) obtained by µXCT imaging (see Sect. 2.3.3) was used to parametrize the surface area \(A\) for core rate normalization. Alternatively, the reactive surface area \(RSA\) of the mineral involved in the reaction can be estimated from the saturation state of the outlet solution according to Rötting et al. (2015)

$$RSA = \frac{{r_{{Cc,{\text{total}}}} }}{{k_{c} \cdot \left( {1 - 10^{SI} } \right)}},$$
(5)

with \({r}_{Cc,\mathrm{total}}\) (in units mol L−1) acquired from the experiments, \({k}_{c}\) the overall rate constant of the reaction (in units mol m−2 s−1), and \(SI\) the saturation index of the fluid. Equation (5) is derived from a general rate law for mineral dissolution (Lasaga 1998) based on the transition state theory (TST)

$$r = k_{c} \cdot A \cdot f\left( {\Delta G} \right),$$
(6)

which includes a function of the Gibbs free energy \(f(\Delta G)\) for scaling the resulting rate as a function of the saturation state (\(f\left(\Delta G\right)=0\) at equilibrium). This saturation state function is not exactly known and can be expressed by different mathematical forms (e.g., Hellmann and Tisserand 2006; Xu et al. 2012). In this study, the simplest form was used (e.g., Luquot and Gouze 2009; Rötting et al. 2015)

$$f\left(\Delta G\right)=1-{10}^{SI}.$$
(7)

If not determined experimentally, the kinetic rate constant \({k}_{c}\) for calcite dissolution can be calculated according to Chou et al. (1989) using the given rate constants (\({k}_{1}\), \({k}_{2}\), \({k}_{3}\), \({k}_{-3}\)) and the activities of the carbonate species in the fluid

$$k_{c} = k_{1} \cdot a_{{H^{ + } }} + k_{2} \cdot a_{{{\text{H}}_{2} {\text{CO}}_{3}^{*} }} + k_{3} \cdot a_{{{\text{H}}_{2} {\text{O}}}} - k_{ - 3} \cdot a_{{{\text{Ca}}^{2 + } }} a_{{{\text{CO}}_{3}^{2 - } }} .$$
(8)

The geochemical code PHREEQC (Parkhurst 1995) with the thermodynamic database phreeqc.dat was used to determine the speciation of the carbonate system and to calculate calcite saturation indices.

X-ray micro-computed tomography

The core plugs were scanned before the flow-through experiments using a Nikon XT H 225 ST X-Ray system with a voxel resolution of 10–13.7 µm in dependence of the sample size. A total of 3600 projections were acquired during the measurement of each core sample. After reconstruction, the images were denoised by applying a non-local means filter (Buades et al. 2005) implemented in the commercial software package GeoDict 2020 (Math2Market GmbH). The advantage over other noise-reducing methods (e.g., Median Filter, Anisotropic Diffusion Filter, Total Variation Filter) is a better signal-to-noise ratio, while sharp phase boundaries are retained (Schlüter et al. 2014). The beam hardening effect was corrected by a hypersurface fitting beam hardening correction filter which normalizes the gray-value intensity drop in the middle of the sample. Segmentation into different phases based on X-ray absorption was done by conventional greyscale thresholding with the software AVIZO (version 2019.1).

The GeoDict module PoroDict was used for all subsequent analyses based on the segmented µXCT images of the core plugs. The total geometric surface area of the calcite cement \(\left( {GSA_{{Cc,{\text{total}}}} } \right)\) was determined using an implemented algorithm by Ohser and Mücklich (2000). The algorithm approximates the surface of a segmented phase by deriving the surface area from all possible spatial configurations of the voxels (Ohser and Mücklich 2000). As only the open porosity was expected to be accessible for the fluid, \(GSA_{{Cc,{\text{total}}}}\) was further scaled by excluding the closed porosity in the sample from the surface area calculation. For normalizing the core scale calcite dissolution rates that were determined indirectly by the measured calcium concentrations in the outlet fluid (Sect. 2.3.2), the geometric surface area of the calcite in contact with the open pore space \(\left( {GSA_{{Cc,{\text{open}}}} } \right)\) was utilized. To compute the open porosity, the Porosimetry function of the GeoDict module PoroDict was applied to extract pores with connectivity to the sample inlet and outlet, considering the actual flow direction in the core experiments (Becker et al. 2020). In addition, the size distribution of the calcite cement clusters within the core plugs was analyzed using an implemented pore size distribution (PSD) algorithm (Granulometry function in PoroDict), which was instead applied to the phase that represented the calcite cement. To determine the cluster size distribution geometrically, the entire volume of the segmented phase under consideration is virtually filled with spheres of different sizes.

Results and discussion

Calcite dissolution rates on mineral surface scale

As described in Sect. 2.2, a polished sandstone core sample slice (E7) was reacted step-wise in the flow cell and the surface height retreat was subsequently quantified by VSI for 12 areas of interest in six different calcite patches. Backscattered electron images of the unreacted and reacted calcite cement can be found in Fig. SI3 in the Supplementary Information. The dissolution of the calcite cement patches was not uniform (Fig. 3). The highest rates were observed for the cement patches m1 and m2 (Fig. 3b, c), which were located closer to the inlet of the cell (Fig. 3a). Overall, dissolution was more pronounced at the left interfaces between the calcite cement patch and the surrounding grains. The VSI height maps for all calcite patches and reaction time intervals are provided in the Supplementary Information.

Fig. 3
figure 3

Dissolution rate maps m1–m6 of the investigated calcite patches (b–g) and a their position in the field of view of the fluid cell. To determine the rates, two distinct areas of interest (as large as possible) were evaluated on each map to exclude unreacted areas (black) from the analysis

Full size image

Based on the 12 areas of interest extracted from the six calcite patches, the arithmetic mean and standard deviation were calculated over all pixels and for each reaction time interval. The calcite dissolution rate at the mineral surface scale did not change significantly in time (Fig. 4a). The calculated average dissolution rate \({r}_{Cc}\) including all investigated cement patches and reaction times was 1.6 ± 0.8 × 10–5 mol m−2 s−1, and corresponds to an average surface height retreat of 3.5 ± 1.7 µm. The most reactive parts of the calcite cement patches retreated by up to 11.2 µm, which corresponds to a dissolution rate of 1.5 × 10–4 mol m−2 s−1. A decreasing tendency of dissolution rates with increasing distance of the investigated calcite patch from the inlet of the fluid cell is suggested in Fig. 4b. Due to the low HRT, it is unlikely that this effect could be governed by chemical gradients, but more experiments would be needed that focus on this behavior. However, the results also show that the variability of rates within the individual areas of interest is much higher (Fig. 4b, standard deviation bars are very variable) than the variability of rates between individual calcite patches (Fig. 4a). These results have similarities with the results obtained by Pedrosa et al. (2019, 2021) for the same rock, where also a surface reactivity variability was identified for the calcite cement, but the reaction rates were significantly lower (~ 1.7 × 10–6 mol m−2 s−1) due to the use of carbonated fluids (pH ~ 8.7). Contrary to the findings in Pedrosa et al. (2021), we did not identify any sharp reactivity interfaces associated with internal differences in the chemical composition, although this could also be a coincidence related to the heterogeneity of the sandstone (Heidsiek et al. 2020). In addition, it is also possible that the rate variability caused by chemical heterogeneity is obscured due to the low pH of the infiltration solution.

Fig. 4
figure 4

Results of the mineral surface dissolution experiments. a Changes in mean dissolution rate with reaction time (all data). The standard deviation indicates the differences between the individual areas of interest; b average dissolution rate (full reaction time) of the 12 areas of interest within the six calcite patches m1–m6 ordered by their relative position within the field of view of the micro-cell. The standard deviation corresponds to the deviation to the average rate inside each calcite patch

Full size image

Calcite dissolution rates on core scale

Results of the flow-through experiments

On the core scale, a total of four core samples were reacted for varying time periods (Table 1). A continuous dissolution of the calcite cement was observed throughout each flow-through experiment. With regard to the mineralogical composition of the sandstone (Sect. 2.1), it was assumed that all calcium present in the solution sampled at the outlet was originating from calcite dissolution. In principle, it is possible that part of the calcium originates from clay minerals in the sandstone, but this contribution would be negligible compared to the amount of calcium originating from calcite dissolution.

Three low-pressure experiments with the triaxial permeability cells (Sect. 2.2.2, core plugs F11, C14, and G12, Fig. 1a) and one high-pressure experiment with the flow-through autoclave (Sect. 2.2.3, sample E6, Fig. 1a) were conducted. The volumetric flow rates in the high-pressure experiment were about three orders of magnitude higher than the flow rates in the low-pressure experiments (Fig. 5a). Accordingly, the hydraulic residence time (HRT) of the reactive fluid varied over three orders of magnitude (Fig. 5b). The calcium concentration in the outflowing solution was higher in the low-pressure experiments than in the high-pressure experiment (Fig. 5c). For all core plugs, the outlet pH was significantly elevated compared to the pH 4.0 infiltration solution, with the highest values occurring in the initial phase (Fig. 5d).

Fig. 5
figure 5

Experimental results for the flow-through experiments with triaxial permeability cells (F11, C14, and G12, triangles) and the flow through-autoclave ICARE4 (sample E6, squares): a Volumetric flow rate and total exchanged pore volumes (PV), b hydraulic residence time within the core plug, c Ca2+ concentration and d pH of the fluid samples at the outlet, and e total dissolution rate

Full size image

The pH of the outlet fluid correlated with the measured Ca2+ concentration (correlation coefficient \(r\) = 0.52). The Ca2+ concentration was directly related to the HRT (\(r\) = 0.64) and the volumetric flow rate (\(r\) =  − 0.63). At the inlet of the core plug, the fluid is highly undersaturated with respect to calcite, but while traveling through the sample, the saturation state shifts toward equilibrium, accompanied by an increase in calcium concentration and pH and a decrease in dissolution rate. As soon as the outlet pH returns to the level of the infiltration solution, it can be assumed that most of the exposed calcite cement in the core plug was dissolved. According to the common estimation procedure based on the calcium concentration curve (e.g., Luquot and Gouze 2009; Luquot et al. 2012), only small portions of the initial calcite volume of 0.6 vol.-% (C14) to 2.7 vol.-% (E6) were dissolved in the flow-through experiments.

Compared to the three low-pressure experiments, the total dissolution rate for E6 was approximately two orders of magnitude higher (Fig. 5e) as expected due to the applied experimental boundary conditions (highest flow rate, cf. Table 1). The total rates obtained for samples F11, C14, and F11 showed a similar range of values and a similar behavior over time. After an initial phase, a stabilization of the rates and therefore an almost steady-state behavior was observed with progressing reaction time. A strong correlation of the measured rates with the µXCT-derived geometric calcite cement surface area in contact with the open pore space \(GSA_{{Cc,{\text{open}}}}\) was evident (\(r\) = 0.98). This surface area parameter, which is discussed in more detail in Sect. 3.2.2, was therefore used for rate normalization (Sect. 3.3).

The dissolution of the calcite cement resulted in a measurable increase in porosity of + 1.6 to + 7.6% with respect to the initial value in all experiments. However, while core plugs F11, C14, and G12 showed a significant increase in permeability with progressing reaction time (+ 6 to + 106%), a strong permeability reduction of 55% was measured for core plug E6. This was most likely caused by illite mobilization and pore throat plugging, as confirmed by scanning electron microscopy (SEM) analysis of the reacted sample material.

Accessibility and geometry of the calcite cement

The µXCT characterization of the core plugs was mainly applied to parametrize the surface area and the fluid accessibility of the calcite cement in the sandstone (Sect. 2.3.3), where it only represents a component of the whole mineral assemblage. Contrastingly, full surface accessibility of the calcite cement is guaranteed in the micro-cell, where the polished core sample slice is overflown by the acidic solution. All parameters and sample properties derived from the segmented µXCT data sets of the unreacted core plugs are summarized in Table 2. Four phases could be identified: “pores”, “grains” (quartz, feldspar, clay-rich lithoclasts), weakly absorbing cements (“cements low”), and highly absorbing cements (“cements high”). The calcite cement in the sandstone was represented by the phase “cements low” and was present in proportions of 6–16 vol.-%, whereas the phase “cements high” mainly comprised barite (0.4–2.8 vol.-%). Despite their spatial proximity within the sandstone block, significant differences in the composition of the core plugs were observed (cf. Supplementary Information, Fig. SI13).

Table 2 Properties of the sandstone samples used for the core scale percolation experiments derived from segmented µXCT images (GSACc denotes the geometric surface area of the calcite cement)
Full size table

As described in Sect. 2.3.3, for calculating the µXCT calcite surface area for the normalization of the core rates, only the interface between the phase “cements low” and the voxels of the open pore network was considered (\(GSA_{{Cc,{\text{open}}}}\), Table 2). Due to the heavy calcite cementation, the Bebertal sandstone is characterized by a very strong heterogeneity already at the mm-scale (Heidsiek et al. 2020). Thus, it was assumed that the parameter \(GSA_{{Cc,{\text{open}}}}\) represents the most appropriate measure to determine the proportion of the calcite surface area that is exposed to the flow field within the different core plugs (hereinafter also referred to as the fluid-accessible surface area). For comparison, the calcite surface area in contact with the total pore space \(\left( {GSA_{{Cc,{\text{total}}}} } \right)\) was also calculated.

The ratio of the two surface area parameters \(GSA_{{Cc,{\text{open}}}} {\text{ and }}GSA_{{Cc,{\text{total}}}}\) (Table 2) also provides a measure for estimating the general fluid accessibility of the calcite cement within a sandstone sample. The \(GSA_{{Cc,{\text{open}}}} {/}GSA_{{Cc,{\text{total}}}}\) ratio ranges between 3% (E6) and 28% (F11). The three-dimensional µXCT images also indicate an increased fluid accessibility of the calcite cement in the core plug F11 (Fig. 6a). A strongly cemented wedge-shaped structure could be identified in the upper part. However, it does not extend over the entire cross-sectional area, thus allowing the fluid to flow past this structure. In the remaining sample volume, the calcite cement forms small individual clusters. The corresponding calcite cluster size distribution in the core also confirms that sample F11 contains the highest proportion of small clusters, which is advantageous for the fluid accessibility (Fig. 6b). Although core plug E6 also has relatively small clusters, the calcite cement was mainly accumulated in inclined layered structures that cut completely through the plug, forcing the fluid to penetrate these cemented layers. In the core plugs C14 and G12, much of the intergranular volume was completely filled with calcite cement. Both samples were characterized by a substantially higher median cluster diameter, and especially G12 showed a high proportion (47 vol.-%) of calcite clusters with diameters of at least 100 µm. However, the cement distribution appears more homogeneous for these samples, which has an advantageous effect with regard to the fluid accessibility of individual clusters, and is expressed by a medium \(GSA_{{Cc,{\text{open}}}} {/}GSA_{{Cc,{\text{total}}}}\) ratio.

Fig. 6
figure 6

a Spatial distribution of the phase “cements low” (calcite) within the four core plugs and b size distribution of the calcite cement clusters. Vertical lines in b indicate the median values. The graphs refer to the initial state of the samples before the experiment

Full size image

To the authors’ knowledge, estimates of the surface area specifically for calcite or carbonate cements in sandstones are not available in the literature. Published values for the specific surface area of pure carbonate materials are in the range of 0.01 m2 g−1 for Iceland spar fragments (Molins et al. 2014) and 0.09–2.5 m2 g−1 for different carbonate rocks (Lai et al. 2015). In contrast, the µXCT surface area of the calcite cement of the Bebertal sandstone varied between 2.0 × 10–7 m2 g−1 and 1.1 × 10–5 m2 g−1 related to the sample mass, and between 1.2 × 10–6 m2 g−1 and 8.1 × 10–5 m2 g−1 related to the calcite mass in the core plug. A direct comparison with the literature values is therefore not possible, because the calcite only makes up a portion of the mineral inventory of the sandstone, and as a cement phase, it is characterized by a completely different geometry.

Comparison of normalized dissolution rates on mineral surface and core scale

To enable a direct comparison of the experimental rate data between the core and mineral surface scale, normalized rates (in units mol m−2 s−1) have to be used to account for the differing system sizes. While VSI allows for a direct determination of surface normalized rates (cf. Eq. (2)), the normalized rates for the core scale had to be calculated indirectly using the fluid-accessible surface area determined by µXCT analysis (cf. Eq. (4)).

The average dissolution rates for the different core plugs varied between 1.6 × 10–7 and 4.9 × 10–6 mol m−2 s−1, and the full range of core dissolution rates was 5.8 × 10–8–8.4 × 10–6 mol m−2 s−1. Compared to the average rate at the mineral surface with identical inlet fluid chemistry (1.6 × 10–5 mol m−2 s−1, Sect. 3.1), the core rates were 0.5–2 orders of magnitude lower (Fig. 7). From previous studies, calcite dissolution rates are known to vary by 1–2 orders of magnitude under controlled laboratory conditions, and up to several orders of magnitude for different scales or rate determination methods (e.g., Arvidson et al. 2003; Fischer et al. 2012a, 2014; Pereira Nunes et al. 2016). The literature data shown in Fig. 7 also indicate a rate variability of about one order of magnitude for pH 4. However, since the literature data mainly comprise far-from-equilibrium rates, and this study compares far-from-equilibrium rates with near-equilibrium rates, an even higher deviation was expected between the core scale and the mineral surface scale.

Fig. 7
figure 7

Dissolution rates at the mineral surface (this study and the same sandstone at pH 8.7 from Pedrosa et al. (2019)), core dissolution rates (this study, square = high-pressure experiment, triangles = low-pressure experiments), and literature calcite dissolution rates (data compilations by Arvidson et al. (2003) and Bollermann and Fischer (2020)). The derived core rates are plotted against both the inlet pH (open symbols) and the mean outlet pH (closed symbols)

Full size image

The existing deviation of the core dissolution rates from the mineral surface rates reflects the strongly differing reactive transport conditions. These can be mapped using several parameters summarized in Table 3, including the HRT, the saturation index, and the Péclet and Damköhler number (details in Supplementary Information, Table SI1).

Table 3 Transport conditions of the experiments on mineral surface scale (micro-cell) and on core scale (triaxial permeability cell, flow-through autoclave ICARE4)
Full size table

The flow through the pore space of the core plugs was slow with an HRT in the order of minutes, leading to a buffering of the solution’s acidity and a successive increase of the calcite saturation index (\(SI\)). This resulted in the formation of strong chemical gradients as indicated by the significant pH difference between the inlet and outlet of each core plug (Fig. 5d). The Damköhler numbers indicate that the characteristic time for fluid transport through the core plug was in the same order of magnitude as the characteristic time for dissolution or, in case of the low-pressure experiments, even higher. The Péclet numbers confirm a diffusion-dominated transport for all core experiments due to the low permeability environment of the Bebertal sandstone with initial rock permeabilities of only 1.1–3.1 mD. In contrast, the micro-cell experiment ensured minimum HRTs and minimum characteristic transport times of the reactive fluid. Far-from-equilibrium conditions were maintained at all times and the flow regime was purely advective with a free flow over the rock surface.

Naturally cemented calcite in sandstones contains variable crystal orientations, different surface morphologies, impurities and grain boundaries, and diverse grain sizes with a variable density of highly reactive crystal corners and edges (Noiriel et al. 2019, 2020; Pedrosa et al. 2019, 2021). The mineral surface rates obtained at pH 4.0 in this study are within the variability of the literature rate data (Fig. 7). At pH 8.7, the same sandstone also showed a variability of rates found in other calcite sample types. This shows a consistency in the intrinsic dissolution rate variability of natural calcite samples, independent of its bulk form (single cleaved crystals, calcite powders, and cement crystals), which is of great importance for the transferability of calcite dissolution rates from prepared sample material to the naturally occurring mineral phase. The higher the pH, the reaction is probably more surface-controlled rather than diffusion-controlled (Arvidson and Morse 2014). The pH of 4.0 in the experiments is a transition pH, where the rate variability is expected to be associated with both transport and surface effects; i.e., a region where complex kinetics occur (Morse et al. 2007).

With exception of core plug G12, the normalized core dissolution rates were ranging between the mineral surface rates that were analyzed for pH values of 4.0 and 8.7 (Pedrosa et al. 2019). Possible reasons for the strong deviation of the rate for G12 are discussed in Sect. 3.4. This strongly suggests that the reported rate discrepancy of several orders of magnitude could be due to an overestimation of the reactive mineral surface area (e.g., usage of single-mineral BET values for components of a multi-mineral rock), rather than solely due to the rate-reducing effect of transport control. If the specific structure and fluid accessibility of the mineral phase of interest are not explicitly considered for surface area quantification (cf. Sect. 3.2.2), or if the surface area is derived from chemically comparable sample material with a completely different geometry (e.g., poikilitic carbonate cement versus micritic limestone), the resulting dissolution rate will most likely be misestimated. The fact that the core rates fit better with the mineral surface dissolution rates at pH 8.7 is plausible, because this value corresponds approximately to the outlet pH measured in the core experiments. Here, the pH of 4.0 only prevails directly at the sample inlet, since the comparatively long transport time through the pore space of the sandstone leads to a significant increase in pH to 6.8–8.8 (Fig. 5d). Thus, even without performing flow-through experiments, a possible range of values for core-scale rates could principally be determined based on existing mineral surface rates, provided that the expected buffering of the pH value can be estimated.

To identify possible influencing factors on the relative order of the core rates in Fig. 7, a correlation analysis (cf. Supplementary Information, Fig. SI14) was performed. The normalized core rates correlated most strongly with the initial permeability of the core plug (\(r\) = 0.81). With decreasing permeability (i.e., pore connectivity), preferential flow becomes more important. Especially for core plug E6, the formation of preferential flow paths was presumably intensified, because this sample was exposed to high differential pressures of up to 19 bar (Sect. 2.2.3). This fact, as well as the reduction of the sample permeability during the experiment (cf. Section 3.2.1), can lead to a reduction of the actual contact surface of the fluid during the experiment which in turn causes lower surface normalized dissolution rates. In addition, due to the larger sample dimensions, the µXCT data set of E6 consists of three stitched scans. Artificial generation of (open) porosity in the overlap regions could also have led to an overestimation of the surface area and thus to an underestimation of the normalized rate. A strong negative correlation with the normalized core rates (\(r\) =  − 0.69) was also found for the median calcite cluster diameter (Fig. 6b). This fits with the fact that the reactivity of minerals generally increases with smaller grain sizes due to the increased contribution of highly reactive features such as corners and edges (e.g., Saldi et al. 2017; Pedrosa et al. 2019; Noiriel et al. 2020).

Comparison of µXCT geometric surface areas with estimated reactive surface areas

To assess the validity of the µXCT-derived surface parameter \({GSA}_{Cc,\mathrm{open}}\) for the normalization of the experimental dissolution rates, it was compared to estimated reactive surface areas (cf. Eq. (5), Sect. 2.3.2). Two different rate constants were used for deriving estimates for the reactive surface area (\(RSA\)) of the calcite cement in the core plugs:

  1. (i)

    Rate constant from the mineral surface dissolution experiments (far-from-equilibrium), reflecting conditions at the inlet of the core plug (\({k}_{c, \mathrm{surface}}\)= 1.63 × 10–5 mol m−2 s−1, Sect. 3.1)

  2. (ii)

    Conservative rate constant (near equilibrium) calculated by Eq. (8) based on the outlet fluid chemistry in the core experiments, reflecting conditions at the outlet of the core plug, (\({k}_{c, \mathrm{fluid}}\) = 5.06 × 10–8 – 8.17 × 10–7 mol m−2 s−1).

By applying Eq. (5) to \({k}_{c, \mathrm{surface}}\) and \({k}_{c, \mathrm{fluid}}\), two end members can be obtained that define the expected range of values for the reactive surface area of the calcite cement in the core sample. Due to the existing variability of various parameters within the sample, such as pH and saturation index \(SI\), only the two end members were considered at this point, while reactive transport modeling (being beyond the scope of this study) could also account for changing conditions along the flow paths. A comparison of \({GSA}_{Cc,\mathrm{open}}\) with the calculated \(RSA\) values shows that three of the four samples are within this range (Fig. 8). Using \({GSA}_{Cc,\mathrm{total}}\), only one value would be within the specified range. Although the two \(RSA\) end members still span over a range of more than an order of magnitude, thus still allowing for misestimation, it can be assumed that the parameter \({GSA}_{Cc,\mathrm{open}}\) provides the most reasonable (measurable) estimates for the studied rock material.

Fig. 8
figure 8

Estimated reactive surface areas (\(RSA\)) for the core plugs using \({k}_{c, \mathrm{surface}}\) from the mineral surface experiments (blue) and \({k}_{c, \mathrm{fluid}}\) estimated from core experiments (red), and µXCT-based geometric surface areas of the calcite cement in contact with the open pore space (\({GSA}_{Cc,\mathrm{open}}\)). The values shown refer to the initial state at the beginning of the experiment

Full size image

For core plug G12, \({GSA}_{Cc,\mathrm{open}}\) was above the specified range and probably overestimates the calcite cement surface area that is available for reaction. As a result, the normalized dissolution rate for G12 was also extremely low (cf. Fig. 7). A possible source of error for this deviation could in principle be an over-segmentation of pore space, although the segmentation process was throughout consistent for all core plugs. Alternatively, an overestimation of the open porosity is possible, which was determined based on a geometric identification of pore networks that are connected to the material surface (Sect. 2.3.3). Due to the fact that G12 was characterized by the largest calcite cluster sizes (Fig. 6b), it is likely that small volumes of the void space that were classified as open porosity by the PoroDict algorithm were actually sealed off during percolation by calcite cement “barriers”, depending on the flow direction. For future studies, the fluid-effective portion of the porosity network for specific flow directions could be identified more precisely by including fluid-flow simulations on the segmented structures (e.g., Jacob et al. 2021).

Noiriel et al. (2020) also used geometric surface areas from µXCT imaging as a parameter for the normalization of calcite dissolution rates. They found a high level of agreement with VSI rates that were obtained for the same sample. Since only a single crystal with a size of 1.8 × 0.6 mm was examined, images with a resolution of 0.325 µm could be achieved (Noiriel et al. 2020). Due to the focus on a single reactive mineral phase in a rock and sample sizes of several centimeters, the surface area calculation in this study is of course limited to the voxel size (10–14 µm). Thus, surface roughness below resolution could not be computed (Table 2).

The transferability to other minerals or lithologies has to be demonstrated on a case-by-case basis. Most importantly, the particular mineral phase has to be optically detectable and thus segmentable in the computed tomography images. In addition, Noiriel et al. (2009) showed that surface area quantification by µXCT is not suitable for materials with high inter-particle microporosity (e.g., sparite and micrite crystals). The applicability of the approach to the studied sandstone can be justified primarily by the fact that the often pore-filling calcite cement mostly forms large contiguous clusters (relative to the voxel size).

Upscaling calcite dissolution rates from mineral surface to core scale

Attempting to link the two scales investigated in this study, the statistical rate information from the mineral surface experiments (Sect. 3.1) was used to retrieve upscaled rates for the core scale and to compare them to the measured values. The upscaling was based on a general rate law for calcite dissolution (Eq. (6), Lasaga 1998), where the resulting rate is described as the product of an intrinsic rate (or rate constant) \({k}_{c}\), a surface area \(A\) (here: \({GSA}_{Cc,\mathrm{open}}\)), and a saturation state function \(f(\Delta G)\). Here, the results of the mineral surface experiments represent the intrinsic rate \({k}_{c}\) of the calcite cement under the chosen fluid chemical conditions of the study. Many authors argue against the use of a single-valued rate constant for predicting dissolution rates and recommend the usage of a multi-rate parametrization to consider the heterogeneity of mineral surface reactivity (e.g., Fischer et al. 2012b; Karimzadeh and Fischer 2021). Thus, the observed variability of the mineral surface rate in space and time was explicitly included in the parametrization of \({k}_{c}\) for the upscaling approach. In this regard, the arithmetic mean and standard deviation over all 12 areas of interest (individual sizes of 651–9730 µm2) within the different calcite cement patches and all reaction time intervals (1.6 ± 0.8 × 10–5 mol m−2 s−1, cf. Section 3.1) was applied.

In addition to the variability of the mineral surface dissolution rate, there is also a variability of the fluid´s saturation state with respect to calcite (expressed by \(f(\Delta G)\)). The temporal variability of this saturation state function can be determined based on the time-dependent fluid sampling in the experiment. Analogous to \({k}_{c}\), also a spatial variability of the fluid´s composition and saturation state exists within the core plug due to the heterogeneity of the pore space that results in a widespread range of fluid velocities (e.g., Al-Khulaifi et al. 2017; Miller et al. 2017; Jacob et al. 2021). However, as this spatial distribution within the sample is not determinable on an experimental basis, \(f(\Delta G)\) was parametrized based on the \(SI\)of the sampled outlet fluid using Eq. (7). The surface area of the reacting mineral also generally evolves with ongoing reaction time (e.g., Lüttge 2006; Luquot and Gouze 2009; Noiriel et al. 2009). A temporal variability of the surface area was not considered for upscaling, because the fluid-accessible geometric surface area from µXCT analysis (Sect. 3.2.2) was only available for the initial state.

A clear relationship between the total dissolution rate of the calcite cement (in mol s−1) and \(A \cdot f\left( {\Delta G} \right)\) across the studied scales was found (Fig. 9a). The mineral surface and core rates are scaled in dependence of the geometric surface area, but the distance to equilibrium must necessarily be considered. Since no fluid chemical data were available for the mineral surface experiments, \(f\left(\Delta G\right)=1\) was assumed, taking into account the hydraulic residence time of less than 4 s (Table 3). The rate data across the two scales can be best described by a power-law function (Fig. 9a). In addition, the linear relationship between the rate and \(A \cdot f\left( {\Delta G} \right)\) is shown, as it would result from Eq. (6) based on the transition state theory. The linear function predicts a stronger increase in dissolution rate with increasing \(A \cdot f\left( {\Delta G} \right)\) than the fitted power-law function; thus, the deviation from the measured rate data broadens with increasing values for \(A \cdot f\left( {\Delta G} \right)\).

Fig. 9
figure 9

a Dependence of the measured dissolution rates on mineral surface and core scale on the product \(A \cdot f\left( {\Delta G} \right)\) with linear dependence (dashed line) according to the transition state theory (TST) and fitted power-law relation (dotted line); b upscaled dissolution rates calculated from the intrinsic rate range (mineral surface experiments) and the sample-specific fluid-accessible surface area and saturation state function

Full size image

Figure 9b shows the upscaled rates calculated by Eq. (6) using the (variable) intrinsic rate measured at the mineral surface (µm-mm-scale) and the sample-specific fluid-accessible surface area and \(f(\Delta G)\). The upscaled rates of the core plugs reacted in the permeability cell (C14, G12, and F11), calculated based on VSI rate data as described above, were misestimated by factors of 0.7–2.9 (deviation of the mean values). Consistent with the above, the largest overestimation by a factor of 7.9 was found for core plug E6 with the largest value for \(A \cdot f\left( {\Delta G} \right)\). Bouissonnié et al. (2018) performed simulations of column experiments on the cm-scale (calcite single crystals embedded in inert material) using VSI-derived rates of the calcite (104) face. While the measured calcite dissolution rates of the column experiment could be reproduced by two-dimensional simulations, they were overestimated by factors of 3 to 20 in the one-dimensional simulations.

Other studies have also shown that models or computations based on volume-averaged parameters tend to overestimate rather than underestimate chemical rates for heterogeneous sample material (Li et al. 2006; Kim et al. 2011), which is also supported by the present results. The high deviation for core plug E6 in particular may also be due to the experimental conditions (i.e., high flow rates and fluid velocities). According to Kim and Lindquist (2013), a larger total change of the surface area as well as a higher spatial variability of local surface area changes can be expected when the dissolution reaction occurs far-from-equilibrium under high flow rates. Since the core plug sample E6 was percolated with the highest flow rate, more pronounced changes in surface area are to be expected compared to the other experiments. This is also supported by the highest dissolved calcite volume during the experiment (cf. Section 3.2.1). Hence, the results for core plug E6 clearly show the importance of considering the temporal variability of the surface area for estimating upscaled rates, especially at higher undersaturation.

Despite the use of sample-averaged parameters for the surface area and the saturation state function, the deviation of the upscaled rates from the measured rates is less than one order of magnitude for all core experiments, which again emphasizes the quality and applicability of the presented methodology to determine the fluid-accessible surface area of the calcite cement. Further improvement of the rate estimations could be achieved by more complex models to account for the temporal and spatial variability of all involved parameters. Still, conceptually, the results show that the statistical rate information on the µm-mm-scale and the rates obtained from the percolation experiments on the core scale can be linked via µXCT parameters such as geometric calcite surface area and connected pore space.

Conclusions

This study compares and links dissolution rates of a natural calcite cement in a reservoir sandstone on length scales from micro- to centimeters. Several experiments with different flow reactors were conducted to investigate the dissolution kinetics of calcite at the mineral surface and on the core scale when exposed to an acidic sodium chloride solution (pH 4).

On the mineral surface scale, the statistical analysis of the calcite surface height retreat measured by vertical scanning interferometry (VSI) under far-from-equilibrium conditions indicated an average rate of 1.6 × 10–5 mol m−2 s−1 with local maximum rates of 1.5 × 10–4 mol m−2 s−1. While the mineral surface dissolution rates on the µm- to mm-scale were in agreement with the literature data for other calcite sample types, the normalized core dissolution rates on the cm-scale deviated by 0.5–2 orders of magnitude from the mineral surface rates, covering a range of 5.8 × 10–8 – 8.4 × 10–6 mol m−2 s−1. For such rock materials, these core rates provide a more realistic guide for estimating effective dissolution rates on even larger scales, since the core experiments were performed under reactive transport conditions that would also be expected to occur naturally in such systems. None of the rates are effectively incorrect, they represent the kinetic response to variable external conditions (i.e., free fluid flow over the rock surface versus fluid percolation in a complex porous medium).

Surface area normalization remains the most critical step in quantifying mineral dissolution rates at the core scale. Based on X-ray micro-computed tomography (µXCT) images of the sandstone core plugs, the geometric surface area of the calcite cement was successfully estimated. The µXCT-derived surface parameter does not simply relate to the surface area of cubic voxels, but approximates the rounded surface of the segmented phase. The additional approach of further scaling the total geometric surface area by considering only the open pore network tangentially along the flow direction allows to evaluate the fluid accessibility of the cement phase in the core plugs. For the samples examined, the proportion of the fluid-accessible calcite surface area to total calcite surface area ranges between 3 and 28%. Despite the limited resolution of the µXCT images, the strong variability of the calcite surface area in the sandstone samples over two orders of magnitude shows how much the surface availability can ultimately vary due to heterogeneity. The methodology used can improve the accuracy of the dissolution rates in multi-mineral samples where a direct surface area measurement (e.g., BET) is not possible.

Using the statistical VSI rate information from the mineral surface scale, the fluid-accessible µXCT geometric surface area and a saturation state function, the total dissolution rate (calcium output in moles per second) for the individual samples on the core scale was estimated and compared to the measured values. The results indicate that for the low-pressure experiments with slow flow rates and conditions close to equilibrium (i.e., low calcite dissolution volumes), total core dissolution rates can be determined with deviations between − 32% and 185%. Due to the higher deviations of the upscaled calcite dissolution rates for the experiment conducted under high differential pressure, the importance of additionally considering the temporal and spatial variability of the available mineral surface as well as the saturation state of the fluid in the pore space became apparent and should be rigorously addressed in future studies.