Skip to main content

Advertisement

SpringerLink
Log in

A novel comprehensive quantitative method for various geological disaster evaluations in underground engineering: multidimensional finite interval cloud model (MFICM)

  • Original Article
  • Published:
Environmental Earth Sciences Aims and scope Submit manuscript

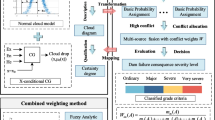
Abstract

The risk prediction of geological disasters exhibits extreme uncertainty and complexity due to the random distribution of evaluation indexes within a finite interval. To improve the accuracy of disaster prediction results, a new evaluation method is in this study suggested to perform a risk evaluation of geological disasters based on multidimensional finite interval cloud model (MFICM) and combination weighting. The MFICM with a transformation between qualitative concept and quantitative data depicts uncertainties and actual distribution features of indexes in the finite interval. Analytic hierarchy process and principal component analysis are adopted to determine the subjective and objective weights of evaluation indexes, respectively, and the combination weight is calculated by a linear method to reduce the influence of subjective factors. The numerical characteristic parameters of each indexes belonging to various risk levels are first calculated based on established evaluation index system. Subsequently, a multi-dimensional finite interval cloud is generated from a forward cloud generator using MATLAB software. Finally, the comprehensive certainty degrees relative to different levels for each sample are determined combined with combination weight, which achieves a mapping of uncertainty between semantic variables and index values. The proposed method is applied to engineering cases regarding three geological disasters, i.e., water inrush, rock burst and collapse. The obtained results with accuracy and results compared with reference methods show that the MFICM is verified to be practical and universal for the risk evaluation of geological disasters, which improves and enriches the theoretical framework of geotechnical engineering disaster risk evaluation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability, Material availability and Code availability

All data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.

Abbreviations

M, M(Ex, En, He):

Qualitative concept

N, N{x 1, x 2, …, x k}:

A universe of discourse

x, x(x 1, x 2, …, x k):

Quantitative number

μ(x), μ(x(x 1, x 2, …, x k)):

Certainty degree

μ c(x(x 1, x 2, …, x k)):

Comprehensive certainty

Ex, (Ex1, Ex2, …, Exk):

Expectation

En, (En1, En2, …, Enk):

Entropy

He, (He1, He2, …, Hek):

Hyper-entropy

[B i min, B i max]:

Bilateral constraints interval

[B i min, + ∞], [0, B i max]:

Unilateral constraint intervals

B i max :

Maximum values of level interval

B i min :

Minimum values of level interval

K :

Cloud droplet number

φ :

Empirical coefficient constant

k :

Dimensions of the cloud model

σ θ/σ c :

Stress coefficient

W et :

Elastic deformation energy

λ max :

Maximum eigenvalues

n :

Order of the judgment matrix

w i :

Subjective weight

P :

Judgment matrix

RI:

Average consistency index

CR:

Consistency index

A t × n :

Data matrix

R :

Correlation coefficient matrix

e i :

Unit eigenvector

f(i):

Principal contribution rate

F(b):

Principal component load

w j :

Objective weight

W :

Combination weight

t :

Risk level number

Q :

Final risk level

σ c / σ t :

Brittle coefficient

K v :

Rock integrity coefficient

AHP:

Analytic hierarchy process

PCA:

Principal component analysis

MFICM:

Multidimensional finite interval cloud model

MNCM:

Multidimensional normal cloud model

RS-TOPSIS:

Rough set-Ideal point method

MABAC:

Multiattributive border approximation area comparison

References

  • Anagnostopoulos KP, Mamanis G (2011) The mean-variance cardinality constrained portfolio optimization problem: an experimental evaluation of five multiobjective evolutionary algorithms. Expert Syst Appl 38:14208–14217

    Google Scholar 

  • Beard AN (2010) Tunnel safety, risk assessment and decision-making. Tunn Undergr Space Technol 25(1):91–94

    Article  Google Scholar 

  • Brown ET (2012) Risk assessment and management in underground rock engineering—an overview. J Rock Mech Geotech Eng 4(3):193–204

    Article  Google Scholar 

  • Cai W, Dou LM, Zhang M, Cao WZ, Shi JQ, Feng LF (2018) A fuzzy comprehensive evaluation methodology for rock burst forecasting using microseismic monitoring. Tunn Undergr Space Technol 80(Oct.):232–245

    Article  Google Scholar 

  • Dalkey N, Helmer O (1963) An experimental application of the DELPHI method to the use of experts. Manag Sci 9(3):458–467

    Article  Google Scholar 

  • Feng XT, Webber S, Ozbay MU, Wang YJ (1996) An expert system on assessing rockburst risks for South African deep gold mines. J Coal Sci Eng 2(2):23–32

    Google Scholar 

  • Gao CL, Li SC, Wang J, Li LP, Lin P (2017) The risk assessment of tunnels based on grey correlation and entropy weight method. Geotech Geol Eng 36(3):1621–1631

    Article  Google Scholar 

  • Guo J, Zhang WX, Zhao Y (2018) A multidimensional cloud model for rockburst prediction. Chin J Rock Mech Eng 37(5):1199–1206 (in Chinese)

    Google Scholar 

  • Kubler S, Robert J, Derigent W, Voisin A, Traon Y (2016) A state-of the-art survey & testbed of fuzzy AHP (FAHP) applications. Expert Syst Appl 65(Dec.):398–422

    Article  Google Scholar 

  • Lai CG, Chen XH, Chen XY, Wang ZL, Wu XS, Zhao SW (2015) A fuzzy comprehensive evaluation model for flood risk based on the combination weight of game theory. Nat Hazards 77(2):1243–1259

    Article  Google Scholar 

  • Li DY, Du Y (2014) Artificial intelligence with uncertainty. National Defense Industry Press, Beijing (in Chinese)

    Google Scholar 

  • Li Z, Liu Y (2010) Single rule reasoning mapping for the two dimensional normal cloud model. Trans Intell Syst 5(5):464–470

    Google Scholar 

  • Li ZC, Yan XF (2018) Ensemble learning model based on selected diverse principal component analysis models for process monitoring. J Chemom 32(6):e3010

    Article  Google Scholar 

  • Li DY, Liu CY, Gan WY (2009) A new cognitive model: cloud model. Int J Intell Syst 24(3):357–375

    Article  Google Scholar 

  • Li SC, Zhou ZQ, Li LP, Xu ZH, Zhang QQ, Shi SS (2013a) Risk assessment of water inrush in karst tunnels based on attribute synthetic evaluation system. Tunn Undergr Space Technol 38(Sep.):50–58

    Article  Google Scholar 

  • Li SC, Zhou ZQ, Li LP, Shi SS, Xu ZH (2013b) Risk evaluation theory and method of water inrush in karst tunnels and its applications. Chin J Rock Mech Eng 32(9):1858–1867 (in Chinese)

    Google Scholar 

  • Li ZQ, Xue YG, Qiu DH, Xu ZH, Zhang XL, Zhou BH, Wang XT (2017) AHP-Ideal Point model for large underground petroleum storage site selection: an engineering application. Sustainability 9(12):2343

    Article  Google Scholar 

  • Liang WZ, Zhao GY, Wu H, Dai B (2019) Risk assessment of rockburst via an extended MABAC method under fuzzy environment. Tunn Undergr Space Technol 83(Jan.):533–544

    Article  Google Scholar 

  • Lin CJ, Zhang M, Zhou ZQ, Li LP, Shi SS, Chen YX, Dai WJ (2020) A new quantitative method for risk assessment of water inrush in karst tunnels based on variable weight function and improved cloud model. Tunn Undergr Space Technol 95:103136

    Article  Google Scholar 

  • Liu QS, Wu J, Zhang XP, Tang LX, Chen B, Li WW, Xu JL (2020) Microseismic monitoring to characterize structure-type rockbursts: a case study of a TBM-excavated tunnel. Rock Mech Rock Eng 53(7):2995–3013

    Article  Google Scholar 

  • Luo D, Ye LL, Sun DC (2020) Risk evaluation of agricultural drought disaster using a grey cloud clustering model in Henan province, China. Int J Disaster Risk Reduct 49:101759

    Article  Google Scholar 

  • Moore B (1981) Principal component analysis in linear systems: controllability, observability, and model reduction. IEEE Trans Autom Control 26(1):17–32

    Article  Google Scholar 

  • Okoli C, Pawlowski SD (2004) The Delphi method as a research tool: an example, design considerations and applications. Inf Manag 42(1):15–29

    Article  Google Scholar 

  • Qiu DH, Li SC, Zhang LW (2013) Study on rockburst intensity prediction based on efficacy coefficient method. Appl Mech Mater 353–356:1277–1280

    Article  Google Scholar 

  • Russenes BF (1974) Analyses of rockburst in tunnels in valley sides. Dissertation, Norwegian Institute of Technology, The Trondheim

  • Saaty TL (1990) Multicriteria decision-making: the analytic hierarchy process. Dissertation, University of Pittsburgh, The United States

  • Saaty TL (2003) Decision-making with the AHP: why is the principal eigenvector necessary. Eur J Oper Res 145(1):85–91

    Article  Google Scholar 

  • Saaty TL (2008) Decision making with the analytic hierarchy process. Int J Serv Sci 1(1):83–98

    Google Scholar 

  • Shafiullah G, Al-Ruwaih FM (2020) Spatial-multivariate statistical analyses to assess water quality for irrigation of the central part of Kuwait. Bull Eng Geol Environ 79(1):27–37

    Article  Google Scholar 

  • Sun JL, Liu BG, Chu ZF, Chen L, Li X (2018) Tunnel collapse risk assessment based on multistate fuzzy Bayesian networks. Qual Reliab Eng Int 34(8):1646–1662

    Article  Google Scholar 

  • Tudes S, Yigiter ND (2010) Preparation of land use planning model using GIS based on AHP: case study Adana-Turkey. Bull Eng Geol Environ 69(2):235–245

    Article  Google Scholar 

  • Wang JA, Park HD (2001) Comprehensive prediction of rockburst based on analysis of strain energy in rocks. Tunn Undergr Space Technol 16(1):49–57

    Article  Google Scholar 

  • Wang YH, Li WD, Lee PKK, Tsui Y, Tham LG (1998) Method of fuzzy comprehensive evaluations for rockburst prediction. Chin J Rock Mech Eng 17(5):493–501 (in Chinese)

    Google Scholar 

  • Wang D, Singh VP, Zhu YS (2007) Hybrid fuzzy and optimal modeling for water quality evaluation. Water Resour Res 43(5):W05415

    Google Scholar 

  • Wang D, Zeng DB, Vijay PS, Xu PC, Liu DF, Wang YK, Zeng XK, Wu JC, Wang LC (2016a) A multidimension cloud model-based approach for water quality assessment. Environ Res 149(Aug.):113–121

    Article  Google Scholar 

  • Wang YC, Yin X, Jing HW, Liu RC, Su HJ (2016b) A novel cloud model for risk analysis of water inrush in karst tunnels. Environ Earth Sci 75(22):1450

    Article  Google Scholar 

  • Wang YC, Jing HW, Yu LY, Su HJ, Luo N (2017) Set pair analysis for risk assessment of water inrush in karst tunnels. Bull Eng Geol Environ 76(3):1199–1207

    Article  Google Scholar 

  • Wang XT, Li SC, Xu ZH, Hu J, Pan DD, Xue YG (2019a) Risk assessment of water inrush in karst tunnels excavation based on normal cloud model. Bull Eng Geol Environ 78(5):3783–3798

    Article  Google Scholar 

  • Wang XT, Li SC, Xu ZH, Li XZ, Lin P, Lin CL (2019b) An interval risk assessment method and management of water inflow and inrush in course of karst tunnel excavation. Tunn Undergr Space Technol 92:103033

    Article  Google Scholar 

  • Wang XT, Li SC, Xu ZH, Lin P, Hu J, Wang WY (2019c) Analysis of factors influencing floor water inrush in coal mines: a nonlinear fuzzy interval assessment method. Mine Water Environ 38(1):81–92

    Article  Google Scholar 

  • Wang XT, Li SC, Xu ZH, Xue YG, Hu J, Li ZQ, Zhang B (2019d) An interval fuzzy comprehensive assessment method for rock burst in underground caverns and its engineering application. Bull Eng Geol Environ 78(7):5161–5176

    Article  Google Scholar 

  • Wang J, Li SC, Li LP, Lin P, Xu ZH, Gao CL (2019e) Attribute recognition model for risk assessment of water inrush. Bull Eng Geol Environ 78(2):1057–1071

    Article  Google Scholar 

  • Wold S, Esbensen K, Geladi P (1987) Principal component analysis. Chemom Intell Lab Syst 2(1–3):37–52

    Article  Google Scholar 

  • Xu ZH, Li SC, Li LP, Chen J, Shi SS (2011) Construction permit mechanism of karst tunnels based on dynamic assessment and management of risk. Chin J Geotech Eng 33(11):1714–1725 (in Chinese)

    Google Scholar 

  • Xue YG, Li ZQ, Qiu DH, Zhang LW, Zhao Y, Zhang XL, Zhou BH (2019) Classification model for surrounding rock based on the PCA-Ideal point method: an engineering application. Bull Eng Geol Environ 78(5):3627–3635

    Article  Google Scholar 

  • Yan HY, Wu D, Huang Y, Wang GY, Shang MS, Xu JJ, Shi XY, Shan K, Zhou BT, Zhao YF (2017) Water eutrophication assessment based on rough set and multidimensional cloud model. Chemom Intell Lab 164:103–112

    Article  Google Scholar 

  • Yao JP, Wang GQ, Xue BL, Wang PZ, Hao FH, Xie G, Peng YB (2019) Assessment of lake eutrophication using a novel multidimensional similarity cloud model. J Environ Manag 248:109259

    Article  Google Scholar 

  • Zhang GH, Jiao YY, Chen LB, Wang H, Li SC (2016) Analytical model for assessing collapse risk during mountain tunnel construction. Can Geotech J 53(2):326–342

    Article  Google Scholar 

  • Zhang LW, Zhang XY, Wu J, Zhao DK, Fu H (2020) Rockburst prediction model based on comprehensive weight and extension methods and its engineering application. Bull Eng Geol Environ 79(9):4891–4903

    Article  Google Scholar 

  • Zhou KP, Lei T, Hu JH (2013) RS-TOPSIS model of rockburst prediction in deep metal mines and its application. Chin J Rock Mech Eng 32(Supp. 2):3705–3711 (in Chinese)

    Google Scholar 

  • Zhou ZQ, Li SC, Li LP, Shi SS, Xu ZH (2015) An optimal classification method for risk assessment of water inrush in karst tunnels based on grey system theory. Geomech Eng 8(5):631–647

    Article  Google Scholar 

  • Zhou KP, Lin Y, Hu JH, Zhou YL (2016) Grading prediction of rockburst intensity based on entropy and normal cloud model. Rock Soil Mech 37(Supp. 1):596–602 (in Chinese)

    Google Scholar 

Download references

Acknowledgements

The research was supported by the National Natural Science Foundation of China (Grant nos. 51504016, 52004017), Fundamental Research Funds for the Central Universities (Grant nos. FRF-BD-17-007A, FRF-TP-19-026A1), and the China Postdoctoral Science Foundation (Grant no. 2020M670138). The authors would like to express appreciation to the Editors and anonymous Reviewers for their valuable and constructive comments relevant to this manuscript.

Author information

Authors and Affiliations

  1. Key Laboratory of Ministry for Efficient Mining and Safety of Metal Mines, University of Science and Technology Beijing, Beijing, 100083, China

    Tianhua Wu, Yongtao Gao, Yu Zhou & Hao Sun

  2. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing, 100083, China

    Tianhua Wu, Yongtao Gao, Yu Zhou & Hao Sun

  3. Department of Resource Engineering, University of Science and Technology Beijing, 30 Xue Yuan Lu (College Road), Beijing, 100083, China

    Yu Zhou

Authors
  1. Tianhua Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yongtao Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hao Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

THW conceived and designed the research, wrote the paper and programmed with MATLAB software; YTG drew the figures, collected and analyzed the data; YZ programmed with MATLAB software and contributed ideas concerning the structure and content of the article; HS reviewed and edited the manuscript.

Corresponding author

Correspondence to Yu Zhou.

Ethics declarations

Conflict of interest

None.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, T., Gao, Y., Zhou, Y. et al. A novel comprehensive quantitative method for various geological disaster evaluations in underground engineering: multidimensional finite interval cloud model (MFICM). Environ Earth Sci 80, 696 (2021). https://doi.org/10.1007/s12665-021-10012-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12665-021-10012-1

Keywords

Search

Navigation