Abstract
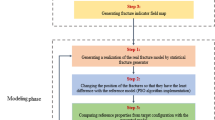
Because modeling the flow of gas and oil in fractured media is increasingly important, multipoint geostatistics approaches, such as single normal equation simulation and FILTERSIM, have become a focus of research in the simulation of sedimentary faces. However, there are problems when these methods are applied to the simulation of discrete fracture networks (DFNs). The biggest problem is that the generated fractures are discontinuous, behaving as separated and isolated points. This paper proposes an improved approach we call CCL-FILTERSIM, which combines FILTERSIM with a run-based, connected-component labeling algorithm to generate more continuous fractures. This paper focuses on the continuity of the simulated fracture network and adopts the scan of the training image, classification of the patterns, and the sequential simulation proposed by FILTERSIM. The principle innovation of the CCL-FILTERSIM approach is the choice of data pattern. Only patterns that form better continuous object patterns are chosen. This is realized by a connected-component labeling algorithm that calculates the connected runs of selected patterns and chooses the pattern with the least runs. Some cases are presented to compare realizations from CCL-FILTERSIM and FILTERSIM, which show that CCL-FILTERSIM yields more continuous objects than FILTERSIM. The DFNs generated by this method provide better conditions for subsequent fluid flow research.




















Similar content being viewed by others
References
Ahmadi R, Masihi M, Rasaei MR, Eskandaridalvand K, Shahalipour R (2014) A sensitivity study of FILTERSIM algorithm when applied to DFN modeling. J Pet Explor Prod Technol 4:153–174
Andersson J, Shapiro AM, Bear J (1984) A stochastic model of a fractured rock conditioned by measured information. Water Resour Res 20(1):79–88
Arpat GB (2005) Sequential Simulation with Patterns (Ph.D. dissertation). Stanford University, Stanford, CA
Baecher GB, Lanney NA, Einstein HH (1977) Statistical description of rock properties and sampling. SPE, ARMA-77-0400. pp 1–8
Chang F, Chen CJ, Lu CJ (2004) A linear-time component-labeling algorithm using contour tracing technique. Comput Vis Image Underst 93(2):206–220
Dershowitz WS, Einstein HH (1988) Characterizing rock joint geometry with joint system models. Rock Mech Rock Eng 21(1):21–51
Dowd PA, Xu CS, Mardia KV, Fowell RJ (2007) A comparison of methods for the stochastic simulation of rock fractures. Math Geol 39(7):697–714
Guardiano FB, Srivastava RM (1993) Multivariate geostatistics: beyond bivariate moments. In: Soares A (ed) Geostatistics Troia. Kluwer Academic, Dordrecht, pp 133–144
He L, Chao Y, Suzuki K (2008) A run-based two-scan labeling algorithm. IEEE Trans Image Process 17(5):749–756
He L, Chao Y, Suzuki K, Wu K (2009) Fast connected-component labeling. Pattern Recogn 42(9):1977–1987
Hestir K, Chiles JP, Long J, Billaux D (1987) Three dimensional modeling of fractures in rock: from data to a regionalized parent-daughter model. American Geophysical Union fall meeting, San Francisco, CA, USA
Honarkhah M, Caers JM (2010) Stochastic simulation of patterns using distance-based pattern modeling. Math Geosci 42:487–517
Hu Q, Qian G, Nowinski WL (2005) Fast connected-component labelling in three-dimensional binary images based on iterative recursion. Comput Vis Image Underst 99(3):414–434
Jiang JM, Younis RM (2015) Numerical Study of complex fracture geometries for unconventional gas reservoirs using a discrete fracture-matrix model. Nat Gas Sci Eng 26:1174–1186
Jin WC, Gao MZ, Yu B, Zhang R, Xie J, Qiu ZQ (2015) Elliptical fracture network modeling with validation in Datong Mine, China. Environ Earth Sci 73(11):7089–7101
Krige DG (1951) A statistical approach to some mine valuation and allied problems on the Witwatersrand (Ph.D. dissertation), University of the Witwatersrand
Lee JS, Veneziano D, Einstein HH (1990) Hierarchical fracture trace model. Rock mechanics Contributions and Challenges: Proc 31st US Symposium, Golden, 18–20 June 1990. Publ. A A Balkema, Rotterdam, pp 261–269
Lumia R, Shapiro L, Zuniga O (1983) A new connected components algorithm for virtual memory computers. Comput Vis Gr Image Process 22(2):287–300
Straubhaar J, Renard P, Mariethoz G, Froidevaux R, Besson O (2011) An improved parallel multiple-point algorithm using a list approach. Math Geosci 43(3):305–328
Strebelle SB (2000) Sequential simulation drawing structures from training images (Ph.D. dissertation). Stanford University, Stanford, CA
Strebelle SB (2002) Conditional simulation of complex geological structures using multiple-point statistics. Math Geosci 34(1):1–21
Tran NH, Chen Z, Rahman SS (2006) Integrated conditional global optimization for discrete fracture network modelling. Comput Geosci 32(1):17–27
Veneziano D (1978) Probabilistic model of joints in rock. Unpublished manuscript, MIT, Cambridge, MA
Warren JE, Root PJ (1963) The behavior of naturally fractured reservoirs. SPE J 3(3):245–255
Wu JB, Zhang TF, Journel A (2008) Fast FILTERSIM simulation with score-based distance. Math Geosci 40:773–788
Xu CS, Dowd P (2010) A new computer code for discrete fracture network modeling. Comput Geosci 36:292–301
Zhang TF (2006) Filter-based training pattern classification for spatial pattern simulation (Ph.D. dissertation). Stanford University, Stanford, CA
Zhang T, Du Y, Huang T, Yang JQ, Li X (2015) Stochastic simulation of patterns using ISOMAP for dimensionality reduction of training images. Comput Geosci 79:82–93
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Key Program) (Grant No. 51534006) and National Natural Science Foundation of China (Grant Nos. 51374181 and 51404206).
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of a Topical Collection in Environmental Earth Sciences on ‘‘Subsurface Energy Storage II’’, guest edited by Zhonghe Pang, Yanlong Kong, Haibing Shao, and Olaf Kolditz.
Appendix
Appendix

For all the pixels, replace the provisional label with the representative label.
Rights and permissions
About this article
Cite this article
Jia, M., Zhang, L. & Guo, J. Combining a connected-component labeling algorithm with FILTERSIM to simulate continuous discrete fracture networks. Environ Earth Sci 76, 327 (2017). https://doi.org/10.1007/s12665-017-6647-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12665-017-6647-0