Skip to main content
SpringerLink
Log in

Spin-polarized optical properties of half-metallic binary XBi (X = Ca, Sr and Ba) compounds in zinc blende and wurtzite phases

  • Original Paper
  • Published:
Indian Journal of Physics Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

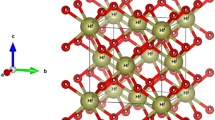
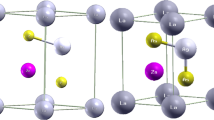
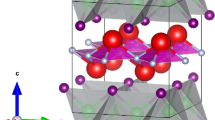
In this work, we aim to study the spin-polarized optical properties of the non-transition metal-based binary compounds XBi (X = Ba, Sr and Ca) in the zinc blende and wurtzite phases. The calculations are performed by the developed full-potential augmented plane wave plus local orbitals (FP-L/APW + lo) method within the spin density functional theory. We used the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (PBE-GGA) and the recently modified Becke–Johnson potential (mBJ-GGA) to generate the exchange–correlation potential. The optical constants as the dielectric function, refractive index and extinction coefficient were calculated and discussed in detail. Our compounds are identified as potential candidates for spintronic applications and high-performance electronic devices, due to their possible half-metallic character. The interband transitions responsible for the structures in the spectra are specified. It is shown that the Bi-p states and (Ca, Sr, Ba)-d states play the major role in optical transitions as initial and final states.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. S Datta and B Das Appl. Phys. Lett. 56 665 (1990)

    Article  ADS  Google Scholar 

  2. R De Groot, F Mueller, P Van Engen and K Buschow Phys. Rev. Lett. 50 2024 (1983)

    Article  ADS  Google Scholar 

  3. K Kusakabe, M Geshi, H Tsukamoto and N Suzuki J. Phys: Condens. Matter 16 S5639 (2004)

    ADS  Google Scholar 

  4. M Sieberer, J Redinger, S Khmelevskyi and P Mohn Phys. Rev. B 73 024404 (2006)

    Article  ADS  Google Scholar 

  5. K L Yao, J L Jiang, Z L Liu and G Y Gao Phys. Lett. A 359 326 (2006)

    Article  ADS  Google Scholar 

  6. G Y Gao, K L Yao, Z L Liu, J Zhang Y Min and S W Fan Phys. Lett. A 372 1512 (2008)

    Article  ADS  Google Scholar 

  7. M Geshi, K Kusakabe, H Nagara, and N Suzuki Phys. Rev. B 76 054433 (2007)

    Article  ADS  Google Scholar 

  8. O Volnianska and P Bogusławski Phys. Rev. B 75 224418 (2007)

    Article  ADS  Google Scholar 

  9. O Volnianska and P Bogusławski Ph. D. thesis (Institute of Physics, Polish Academy of Sciences in Warsaw) (2009)

  10. R R Palanichamy, G S Priyanga, A J Cinthia, A Murugan, A A Meenaatci and Kiyakutti J. Magn. Magn. Mater. 346 26 (2013)

    Article  ADS  Google Scholar 

  11. T Hu, A Hashmi and J Hong Sci. Rep. 4 6059 (2014)

    Article  ADS  Google Scholar 

  12. J P Perdew, K Burke and M Ernzerhof Phys. Rev. Lett. 77 3865 (1996)

    Article  ADS  Google Scholar 

  13. F Tran and P Blaha Phys. Rev. Lett. 102 226401 (2009)

    Article  ADS  Google Scholar 

  14. P Hohenberg and W Kohn Phys. Rev. 136 B864 (1964)

    Article  ADS  Google Scholar 

  15. W Kohn and L J Sham Phys. Rev. 140 A1133 (1965)

    Article  ADS  Google Scholar 

  16. O K Andersen Phys. Rev. B 12 3060 (1975)

    Article  ADS  Google Scholar 

  17. D J Singh and L Nordstro (Planewaves, Pseudopotentials, and the LAPW Method: Springer, Berlin) (2005)

    Google Scholar 

  18. P Blaha, K Schwarz, G Madsen, D Kvasnicka, and J Luitz (An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties: Vienna University of Technology, Austria) (2012)

  19. P E Blöchl, O Jepsen and O K Andersen Phys. Rev. B 49 16223 (1994)

    Article  ADS  Google Scholar 

  20. R John and S Padmavathi Cryst. Struct. Theory Appl. 5 24 (2016)

    Google Scholar 

  21. A Reshak, H Huang, H Kamarudin and S Auluck J. Appl. Phys. 117 085703 (2015)

    Article  ADS  Google Scholar 

  22. A H Reshak and S Auluck Phys. Rev. B 68 245113 (2003)

    Article  ADS  Google Scholar 

  23. A Reshak and W Khan J. Alloys Compd. 592 92 (2014)

    Article  Google Scholar 

  24. C Okoye J Phys: Condens. Matt. 15 5945 (2003)

    Article  ADS  Google Scholar 

  25. A M Fox and M Fox (Optical properties of solids: Oxford University Press, New York) (2010)

    MATH  Google Scholar 

  26. J Sun, H T Wang, J He and Y Tian Phys. Rev. B 71 125132 (2005)

    Article  ADS  Google Scholar 

  27. F Wooten (Optical Properties of Solids 1972, Academic: New York, NY, p. 49) (1972)

    Google Scholar 

  28. A P Sakhya, D Rai, A Dutta, R Thapa and T Sinha RSC Adv. 6 59988 (2016)

    Article  Google Scholar 

  29. D R Penn Phys. Rev. 128 2093 (1962)

    Article  ADS  Google Scholar 

  30. M Fox (Optical properties of solids. Oxford master series in condensed matter physics, ed: Oxford University Press, Oxford) (2001)

    Google Scholar 

  31. F Kong and G Jiang Physica B: Condens. Matter. 404 2340 (2009)

    Article  ADS  Google Scholar 

  32. R Ahuja, O Eriksson, B Johansson, S Auluck and J Wills Phys. Rev. B 54 10419 (1996)

    Article  ADS  Google Scholar 

  33. G Shwetha and V Kanchana Phys. Rev. B 86 115209 (2012)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire de Modélisation et Simulation en Sciences des Matériaux, Université Djillali Liabès de Sidi Bel-Abbès, 22000, Sidi Bel-Abbès, Algeria

    S. Benatmane, L. Beldi, H. Bendaoud, S. Méçabih, B. Abbar & B. Bouhafs

Authors
  1. S. Benatmane
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. Beldi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H. Bendaoud
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. S. Méçabih
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. B. Abbar
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. B. Bouhafs
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. Abbar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Benatmane, S., Beldi, L., Bendaoud, H. et al. Spin-polarized optical properties of half-metallic binary XBi (X = Ca, Sr and Ba) compounds in zinc blende and wurtzite phases. Indian J Phys 93, 627–638 (2019). https://doi.org/10.1007/s12648-018-1333-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12648-018-1333-y

Keywords

PACS No.

Search

Navigation