Skip to main content
SpringerLink
Log in

A Jacobi elliptic function method for nonlinear arrays of vortices

  • Original Paper
  • Published:
Indian Journal of Physics Aims and scope Submit manuscript

Abstract

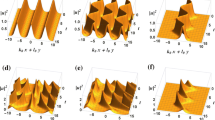
Arrays of vortices are considered for two-dimensional inviscid flows when the functional relationship between the stream function and the vorticity is hyperbolic sine, exponential, sine, and power functions. The Jacobi elliptic function method with symbolic computation is extended to these nonlinear equations for constructing their doubly periodic wave solutions. The different Jacobi function expansions may lead to new Jacobi doubly periodic wave solutions, triangular periodic solutions and soliton solutions. In addition, as an illustrative sample, the properties for the Jacobi doubly periodic wave solutions of the nonlinear equations are shown with some figures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Z Jia-Min et al Chin. Phys. 13 798 (2004)

    Article  ADS  Google Scholar 

  2. C Q Dai et al Opt. Lett. 35 1437 (2010)

    Article  ADS  Google Scholar 

  3. Z Liang et al Chin. Phys. B 17 403 (2008)

    Article  ADS  Google Scholar 

  4. S A S Ahmed and L Buragohain Indian J. Phys. 84 741 (2010)

    Article  Google Scholar 

  5. D K Choudhury and R Choudhury Indian J. Phys. 86 377 (2012); A Jahan and D K Choudhury Indian J. Phys. 84 587 (2010); D K Choudhury and S Islam Indian J. Phys. 85 319 (2011)

  6. A H Bhrawy et al Results Math. doi:10.1007/s00025-011-0225-7 (2012)

  7. R Hirota Phys. Rev. Lett. 27 1192 (1971)

    Article  ADS  MATH  Google Scholar 

  8. A M Wazwaz Appl. Math. Comput. 201 489 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  9. M L Wang Phys. Lett. A 199 169 (1995)

    Article  MathSciNet  ADS  Google Scholar 

  10. E Fan and J Zhang Phys. Lett. A 305 383 (2002)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  11. T Okabe and T Kondou J. Sound Vib. 320 339 (2009)

    Article  ADS  Google Scholar 

  12. A Malik, F Chand, H Kumar and S C Mishra Indian J. Phys. 86 129 (2012); H Kumar, A Malik, F Chand and S C Mishra Indian J. Phys. 86 819 (2012)

  13. A Biswas and E V Krishnan Indian J. Phys. 85 1513 (2011)

    Article  ADS  Google Scholar 

  14. X Zheng et al Phys. Lett. A 311 145 (2003)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  15. C Dai et al Comput. Math. Appl. 56 55 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. H Jia et al J. Math. Anal. Appl. 339 982 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. S Shen and L Jiang J. Comput. Appl. Math. 233 585 (2009)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  18. G Q Xu and Z B Li Comput. Phys. Commun. 161 65 (2004)

  19. G Q Xu Comput. Phys. Commun. 180 1137 (2009)

  20. Q Liu and J M Zhu Phys. Lett. A 352 233 (2006)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  21. C L Bai and H Zhao Phys. Lett. A 355 32 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  22. P G Saffman Vortex Dynamics (Cambridge: Cambridge University Press) (1992)

  23. P K Khosla and S Abdallaha Comput. Fluids 35 670 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  24. G R Flierl Annu. Rev. Fluid Mech. 19 493–530 (1987)

  25. Y Couder and C Basdevant J. Fluid. Mech. 173 225 (1986)

    Article  ADS  Google Scholar 

  26. S Danilov and D Gurarie Phys. Rev. E 63 61208 (2001)

    Article  ADS  Google Scholar 

  27. R T Pierrehumbert and S E Widnall J. Fluid Mech. 102 301 (1981)

    Article  ADS  MATH  Google Scholar 

  28. G J F van Heijst and R C Kloosterziel Nature 340 212 (1989)

    Article  Google Scholar 

  29. E J Hopfinger and G J F van Heijst Annu. Rev. Fluid Mech. 25 241 (1993)

    Article  ADS  Google Scholar 

  30. J M Nguyen Duc and J Sommeria J. Fluid Mech. 192 175 (1988)

    Article  ADS  Google Scholar 

  31. N F Bondarenko and M Z Gak Bull. (Izv.) Acad. Sci. (USSR) Atmos. Ocean. Phys. 14 207 (1978)

  32. L R Ford Automorphic Functions (New York: Chelsea) (1951)

  33. N I Akhiezer Elements of the Theory of Elliptic Functions (Providence: American Mathematical Society) (1990)

  34. G M Zaslavsky et al Weak chaos and quasiregular structures (Cambridge University Press) (1991)

  35. H Lamb Hydrodynamics (Cambridge: Cambridge University Press) (1932)

  36. V V Meleshko and G J F van Heijst J. Fluid Mech. 272 157 (1994)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  37. A C Ting et al Phys. Rev. Lett. 53 1348 (1984)

    Article  ADS  Google Scholar 

  38. K W Chow et al Phys. Fliuds 15 2437 (2003)

    Article  ADS  Google Scholar 

  39. D Montgomery et al Phys. Fluids A 4 3 (1992)

    Article  ADS  MATH  Google Scholar 

  40. D Gurarie and K W Chowb Phys. Fluids 16 9 (2004)

    Article  Google Scholar 

  41. B N Kuvshinov and T J Schep Phys. Fluids 12 3282 (2000)

  42. K W Chow et al Phys. Fluids 15 2437 (2003)

    Article  MathSciNet  ADS  Google Scholar 

  43. J T Stuart J. Fluid Mech. 29 417–440 (1967)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, 21589, Saudi Arabia

    A. H. Bhrawy & M. M. Tharwat

  2. Department of Mathematics, Faculty of Science, Beni Suef University, Beni Suef, 62511, Egypt

    A. H. Bhrawy, M. M. Tharwat & M. A. Abdelkawy

  3. Department of Mathematics, Faculty of Science, Ege University, Bornova-Izmir, 35040, Turkey

    A. Yildirim

Authors
  1. A. H. Bhrawy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. M. Tharwat
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Yildirim
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. A. Abdelkawy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Yildirim.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bhrawy, A.H., Tharwat, M.M., Yildirim, A. et al. A Jacobi elliptic function method for nonlinear arrays of vortices. Indian J Phys 86, 1107–1113 (2012). https://doi.org/10.1007/s12648-012-0173-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12648-012-0173-4

Keywords

PACS Nos.

Search

Navigation